4.3.3 余角和补角 练习题 (含答案) 2023-2024学年人教版七年级数学上册
文档属性
| 名称 | 4.3.3 余角和补角 练习题 (含答案) 2023-2024学年人教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 233.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 19:50:37 | ||
图片预览



文档简介
4.3.3 余角和补角
一、单项选择题
1.与30°的角互为余角的角的度数是( )
A.30° B.60° C.70° D.90°
2.已知∠α=60°32′,则∠α的余角是( )
A.29°28′ B.29°68′ C.119°28′ D.119°68′
3. ∠1与∠2互余,那么∠1的补角是( )
A.180°+∠1 B.90°+∠1 C.90°+∠2 D.90°-∠2
4. 如图,下列说法中错误的是( )
A.OA方向是北偏东30° B.OB方向是北偏西15°
C.OC方向是南偏西25° D.OD方向是东南方向
5. 如图,从点B看点A,点A所在的方向为( )
A. 南偏东58° B.北偏西32° C.南偏东32° D.西偏北58°
6. 如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子:①90°-∠β;②∠α-90°;③(∠α+∠β);④(∠α-∠β).其中正确的有( )
A.4个 B.3个 C.2个 D.1个
7. 岛A和岛B处于东西方向的一条直线上,由岛A、岛B分别测得船C位于北偏东
40°和北偏西50°方向上,下列符合条件的示意图是( )
8. 如图,点A位于点O北偏西60°方向上,点B位于点O南偏西20°方向上,则∠AOB的度数是( )
A.120° B.100° C.80° D.70°
9. 如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是( )
A.图① B.图② C.图③ D.图④
二、填空题
10. 如图,∠AOC=∠COE=∠BOD=90°,则图中与∠BOC相等的角为__________,与∠BOC互余的角为______________,与∠BOC互补的角为__________.
11. 若∠α=∠β,且∠α+∠1=180°,∠β+∠2=180°,则∠1与∠2的关系为
_____,依据是_______________.
12. 已知∠α=59°20′,若∠α与∠β互余,且∠β与∠γ互余,则∠γ的度数为_________.
13. 如图,甲从点A出发向北偏东70°方向走50m至点B,乙从点A出发向南偏西15°方向走60m至点C,则∠BAC的度数是________.
三、解答题
14. 如图,∠AOB与∠AOD的度数的比是2∶11,∠AOC=∠BOD=90°,求∠AOB,∠BOC的度数.
15. 如图,已知∠ABP与∠CBP互余,∠CBD=32°,BP平分∠ABD.求∠ABP的度数.
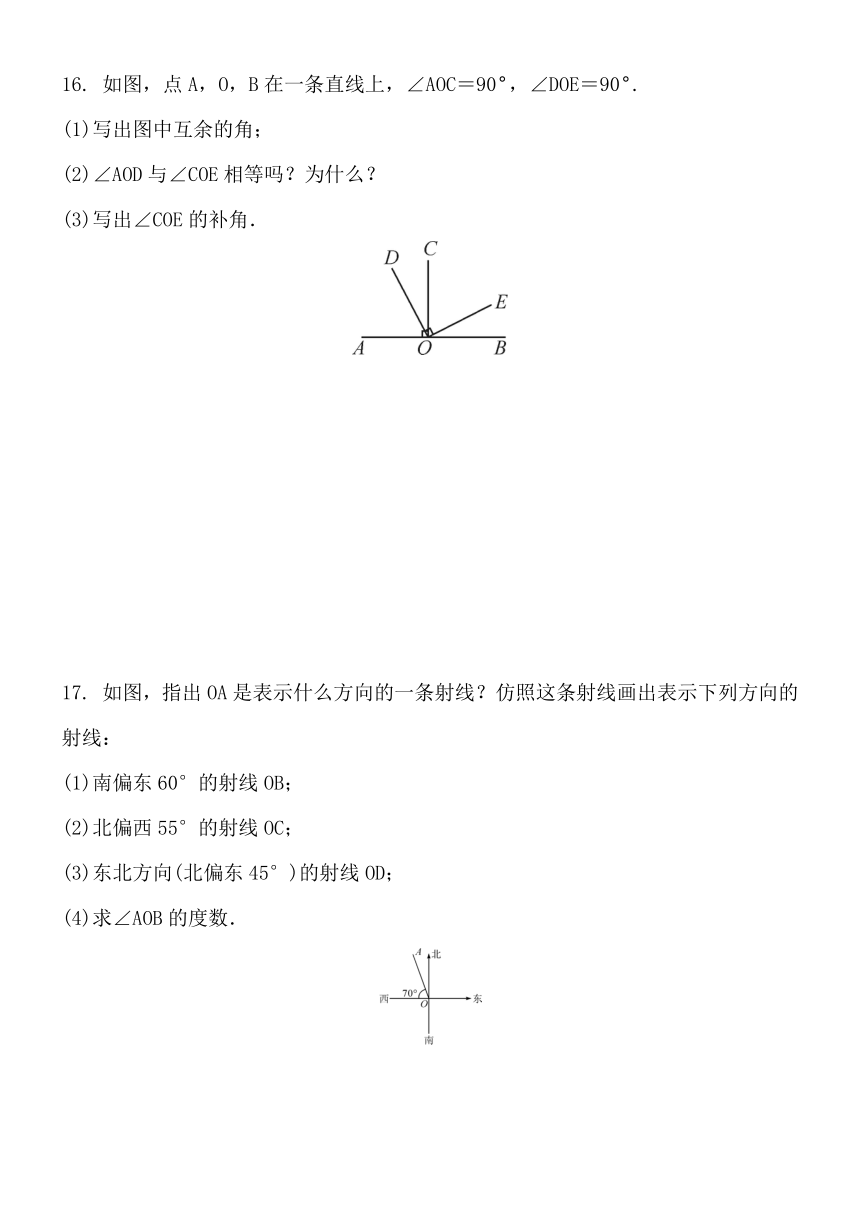
16. 如图,点A,O,B在一条直线上,∠AOC=90°,∠DOE=90°.
(1)写出图中互余的角;
(2)∠AOD与∠COE相等吗?为什么?
(3)写出∠COE的补角.
17. 如图,指出OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
(1)南偏东60°的射线OB;
(2)北偏西55°的射线OC;
(3)东北方向(北偏东45°)的射线OD;
(4)求∠AOB的度数.
18. 如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数;
(2)若轮船C在∠APB的平分线上,则轮船C在灯塔P的什么方位?
19. 图①,将一副三角尺的直角顶点重合在点O处.
(1)①∠AOD和∠BOC相等吗?说明理由;
②∠AOC和∠BOD在数量上有何关系?说明理由;
(2)若将等腰的三角尺绕点O旋转到如图②的位置.
①∠AOD和∠BOC相等吗?说明理由;
②∠AOC和∠BOD的以上关系还成立吗?说明理由.
20. 定义:若α-β=90°,且90°<α<180°,则我们称β是α的差余角.例如:若α=110°,则α的差余角β=20°.
(1)如图①,点O在直线AB上,射线OE是∠BOC的平分线,若∠COE是∠AOC的差余角,求∠BOE的度数;
(2)如图②,点O在直线AB上,若∠BOC是∠AOE的差余角,那么∠BOC与∠BOE有什么数量关系;
(3)如图③,点O在直线AB上,若∠COE是∠AOC的差余角,且OE与OC在直线AB的同侧,请你探究是否为定值?若是,请求出定值;若不是,请说明理由.
答案:
一、
1-9 BACAC ADBA
二、
10. ∠DOE ∠AOB,∠COD ∠AOD
11. 相等 等角的补角相等
12. 59°20′
13. 125°
三、
14. 解:设∠AOB=2x°,则∠AOD=11x°,因为∠AOC=∠BOD=90°,
所以∠AOB=∠COD=2x°,
所以∠BOC=∠AOD-∠AOB-∠COD=11x°-2x°-2x°=7x°,
又∠AOC=90°,所以2x+7x=90,解得x=10,
所以∠AOB=2x°=20°,∠BOC=7x°=70°
15. 解:因为∠ABP与∠CBP互余,所以∠ABP+∠CBP=90°,即∠ABC=90°,
因为∠CBD=32°,所以∠ABD=90°+32°=122°,
因为BP平分∠ABD,所以∠ABP=∠ABD=×122°=61°.
16. 解:(1)互余的角有∠AOD与∠DOC,∠AOD与∠BOE,∠DOC与∠COE,∠COE与∠BOE
(2)相等.理由:∠AOD与∠COE都是∠DOC的余角,同角的余角相等
(3)∠BOD
17. 解:OA表示北偏西20°.
(1)(2)(3)画图如图所示
(4)∠AOB=140°
18. 解:(1)由题意可知∠APN=30°,∠BPS=70°,所以∠APB=180°-∠APN-∠BPS=80°.
(2)因为PC平分∠APB,∠APB=80°,所以∠APC=∠APB=40°,
所以∠NPC=∠APN+∠APC=70°,所以轮船C在灯塔P的北偏东70°的方向上.
19. 解:(1)①∠AOD=∠BOC.理由略 ②∠AOC+∠BOD=180°.理由略
(2)①∠AOD=∠BOC.理由略 ②成立.理由略
20. 解:(1)因为OE是∠BOC的角平分线,所以∠COE=∠BOE,因为∠COE是∠AOC的差余角,所以∠AOC-∠COE=90°,因为∠AOC+∠BOC=180°,所以∠BOC=60°,所以∠BOE=30°.
(2)因为∠BOC是∠AOE的差余角,
所以∠AOE-∠BOC=∠AOC+∠COE-∠COE-∠BOE=∠AOC-∠BOE=90°,
因为∠AOC+∠BOC=180°,所以∠BOC+∠BOE=90°.
(3)是定值.因为∠COE是∠AOC的差余角,所以∠AOC-∠COE=90°,
所以∠AOC=90°+∠COE,∠BOC=90°-∠COE,所以∠AOC-∠BOC=2∠COE,
所以=2.
一、单项选择题
1.与30°的角互为余角的角的度数是( )
A.30° B.60° C.70° D.90°
2.已知∠α=60°32′,则∠α的余角是( )
A.29°28′ B.29°68′ C.119°28′ D.119°68′
3. ∠1与∠2互余,那么∠1的补角是( )
A.180°+∠1 B.90°+∠1 C.90°+∠2 D.90°-∠2
4. 如图,下列说法中错误的是( )
A.OA方向是北偏东30° B.OB方向是北偏西15°
C.OC方向是南偏西25° D.OD方向是东南方向
5. 如图,从点B看点A,点A所在的方向为( )
A. 南偏东58° B.北偏西32° C.南偏东32° D.西偏北58°
6. 如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子:①90°-∠β;②∠α-90°;③(∠α+∠β);④(∠α-∠β).其中正确的有( )
A.4个 B.3个 C.2个 D.1个
7. 岛A和岛B处于东西方向的一条直线上,由岛A、岛B分别测得船C位于北偏东
40°和北偏西50°方向上,下列符合条件的示意图是( )
8. 如图,点A位于点O北偏西60°方向上,点B位于点O南偏西20°方向上,则∠AOB的度数是( )
A.120° B.100° C.80° D.70°
9. 如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是( )
A.图① B.图② C.图③ D.图④
二、填空题
10. 如图,∠AOC=∠COE=∠BOD=90°,则图中与∠BOC相等的角为__________,与∠BOC互余的角为______________,与∠BOC互补的角为__________.
11. 若∠α=∠β,且∠α+∠1=180°,∠β+∠2=180°,则∠1与∠2的关系为
_____,依据是_______________.
12. 已知∠α=59°20′,若∠α与∠β互余,且∠β与∠γ互余,则∠γ的度数为_________.
13. 如图,甲从点A出发向北偏东70°方向走50m至点B,乙从点A出发向南偏西15°方向走60m至点C,则∠BAC的度数是________.
三、解答题
14. 如图,∠AOB与∠AOD的度数的比是2∶11,∠AOC=∠BOD=90°,求∠AOB,∠BOC的度数.
15. 如图,已知∠ABP与∠CBP互余,∠CBD=32°,BP平分∠ABD.求∠ABP的度数.
16. 如图,点A,O,B在一条直线上,∠AOC=90°,∠DOE=90°.
(1)写出图中互余的角;
(2)∠AOD与∠COE相等吗?为什么?
(3)写出∠COE的补角.
17. 如图,指出OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
(1)南偏东60°的射线OB;
(2)北偏西55°的射线OC;
(3)东北方向(北偏东45°)的射线OD;
(4)求∠AOB的度数.
18. 如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数;
(2)若轮船C在∠APB的平分线上,则轮船C在灯塔P的什么方位?
19. 图①,将一副三角尺的直角顶点重合在点O处.
(1)①∠AOD和∠BOC相等吗?说明理由;
②∠AOC和∠BOD在数量上有何关系?说明理由;
(2)若将等腰的三角尺绕点O旋转到如图②的位置.
①∠AOD和∠BOC相等吗?说明理由;
②∠AOC和∠BOD的以上关系还成立吗?说明理由.
20. 定义:若α-β=90°,且90°<α<180°,则我们称β是α的差余角.例如:若α=110°,则α的差余角β=20°.
(1)如图①,点O在直线AB上,射线OE是∠BOC的平分线,若∠COE是∠AOC的差余角,求∠BOE的度数;
(2)如图②,点O在直线AB上,若∠BOC是∠AOE的差余角,那么∠BOC与∠BOE有什么数量关系;
(3)如图③,点O在直线AB上,若∠COE是∠AOC的差余角,且OE与OC在直线AB的同侧,请你探究是否为定值?若是,请求出定值;若不是,请说明理由.
答案:
一、
1-9 BACAC ADBA
二、
10. ∠DOE ∠AOB,∠COD ∠AOD
11. 相等 等角的补角相等
12. 59°20′
13. 125°
三、
14. 解:设∠AOB=2x°,则∠AOD=11x°,因为∠AOC=∠BOD=90°,
所以∠AOB=∠COD=2x°,
所以∠BOC=∠AOD-∠AOB-∠COD=11x°-2x°-2x°=7x°,
又∠AOC=90°,所以2x+7x=90,解得x=10,
所以∠AOB=2x°=20°,∠BOC=7x°=70°
15. 解:因为∠ABP与∠CBP互余,所以∠ABP+∠CBP=90°,即∠ABC=90°,
因为∠CBD=32°,所以∠ABD=90°+32°=122°,
因为BP平分∠ABD,所以∠ABP=∠ABD=×122°=61°.
16. 解:(1)互余的角有∠AOD与∠DOC,∠AOD与∠BOE,∠DOC与∠COE,∠COE与∠BOE
(2)相等.理由:∠AOD与∠COE都是∠DOC的余角,同角的余角相等
(3)∠BOD
17. 解:OA表示北偏西20°.
(1)(2)(3)画图如图所示
(4)∠AOB=140°
18. 解:(1)由题意可知∠APN=30°,∠BPS=70°,所以∠APB=180°-∠APN-∠BPS=80°.
(2)因为PC平分∠APB,∠APB=80°,所以∠APC=∠APB=40°,
所以∠NPC=∠APN+∠APC=70°,所以轮船C在灯塔P的北偏东70°的方向上.
19. 解:(1)①∠AOD=∠BOC.理由略 ②∠AOC+∠BOD=180°.理由略
(2)①∠AOD=∠BOC.理由略 ②成立.理由略
20. 解:(1)因为OE是∠BOC的角平分线,所以∠COE=∠BOE,因为∠COE是∠AOC的差余角,所以∠AOC-∠COE=90°,因为∠AOC+∠BOC=180°,所以∠BOC=60°,所以∠BOE=30°.
(2)因为∠BOC是∠AOE的差余角,
所以∠AOE-∠BOC=∠AOC+∠COE-∠COE-∠BOE=∠AOC-∠BOE=90°,
因为∠AOC+∠BOC=180°,所以∠BOC+∠BOE=90°.
(3)是定值.因为∠COE是∠AOC的差余角,所以∠AOC-∠COE=90°,
所以∠AOC=90°+∠COE,∠BOC=90°-∠COE,所以∠AOC-∠BOC=2∠COE,
所以=2.
