24.1.2垂直于弦的直径 同步练习(含答案) 2023-—2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1.2垂直于弦的直径 同步练习(含答案) 2023-—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 583.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 19:52:37 | ||
图片预览

文档简介
垂直于弦的直径
一、单选题
1.如图,是的直径,弦于点E,,,则的长为( )
A.5 B.3 C.2 D.1.5
2.如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
A.40° B.45° C.50° D.60°
3.一块圆形宣传标志牌简图如图所示,点,,在上,垂直平分于点,现测得,,则圆形标志牌的半径为( )
A. B. C. D.
4.如图,AB为⊙O的直径,弦CD与AB交于点E.若AC=AE,CE=4,DE=6,则的值为( )
A. B. C. D.
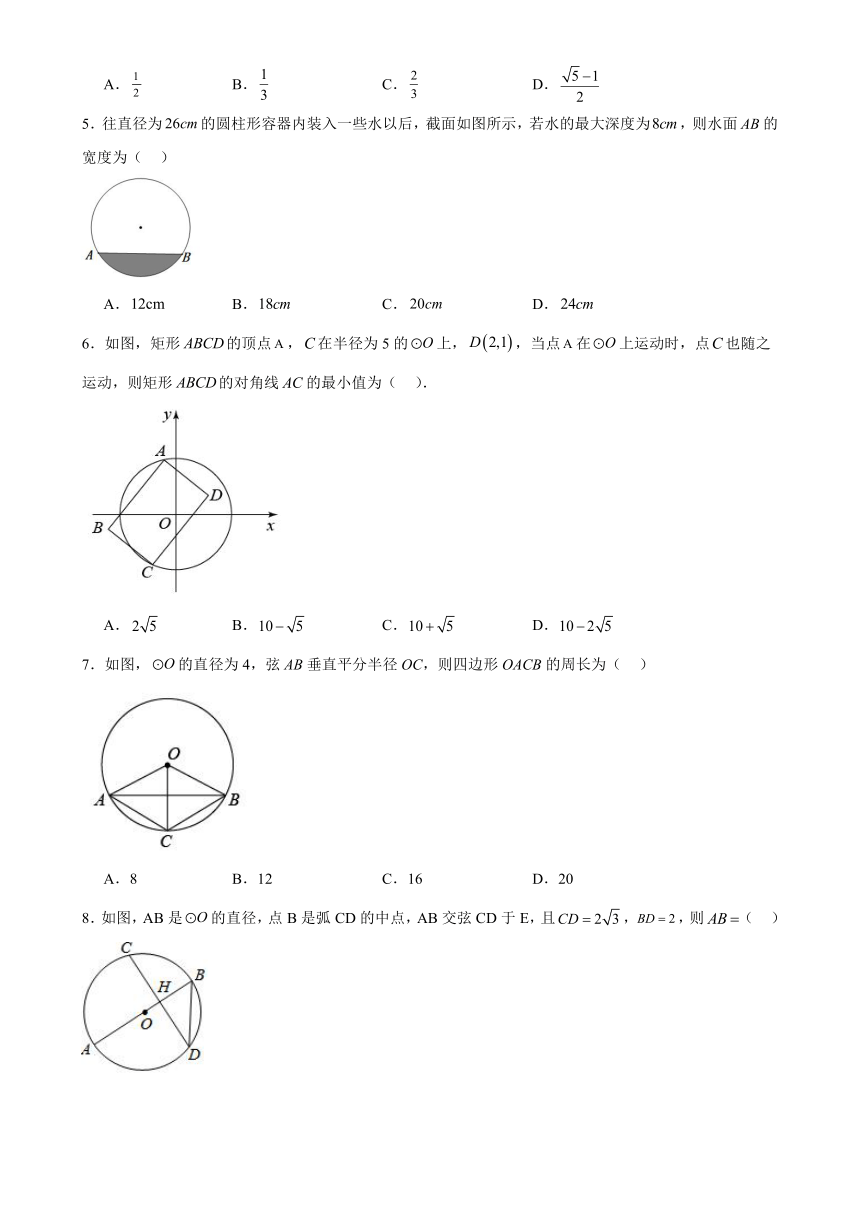
5.往直径为的圆柱形容器内装入一些水以后,截面如图所示,若水的最大深度为,则水面的宽度为( )
A. B. C. D.
6.如图,矩形的顶点,在半径为5的上,,当点在上运动时,点也随之运动,则矩形的对角线的最小值为( ).
A. B. C. D.
7.如图,的直径为4,弦AB垂直平分半径OC,则四边形OACB的周长为( )
A.8 B.12 C.16 D.20
8.如图,AB是的直径,点B是弧CD的中点,AB交弦CD于E,且,,则( )
A.2 B.3 C.4 D.5
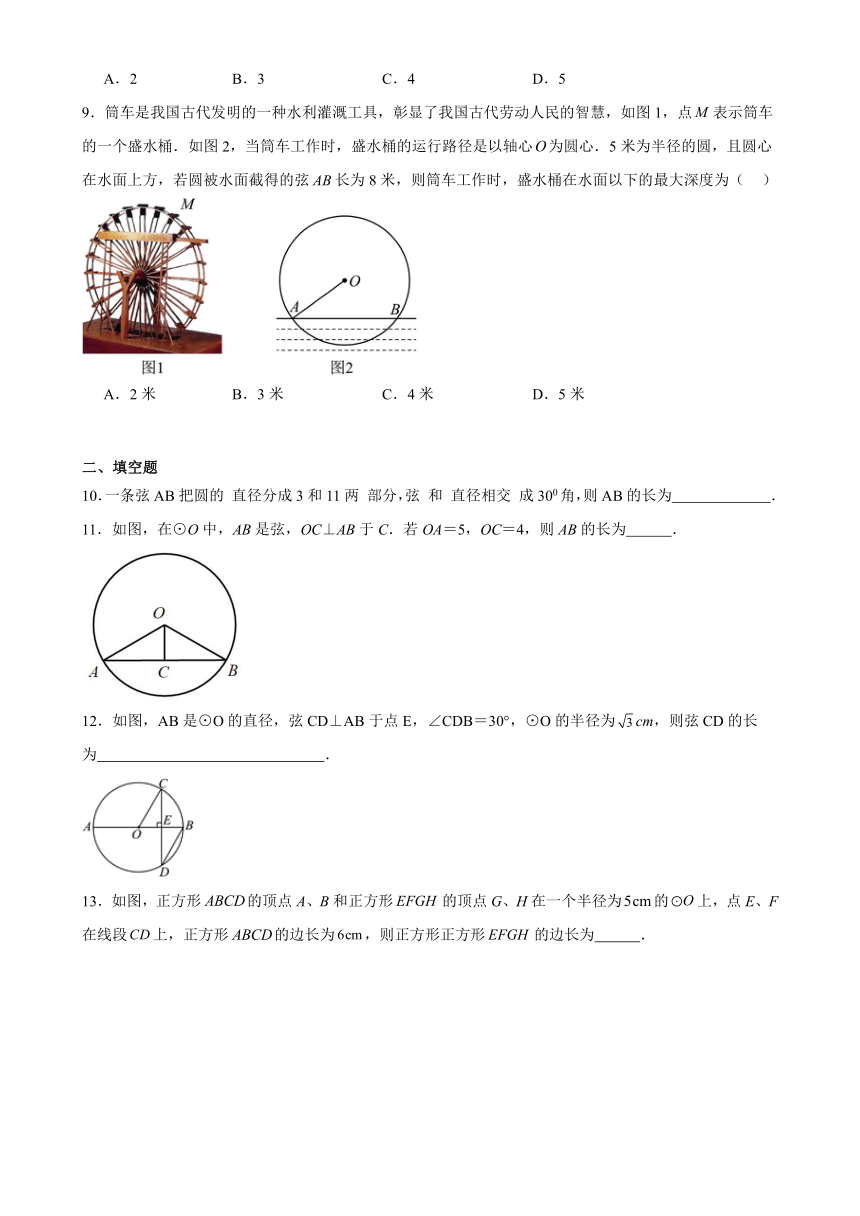
9.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心为圆心.5米为半径的圆,且圆心在水面上方,若圆被水面截得的弦长为8米,则筒车工作时,盛水桶在水面以下的最大深度为( )
A.2米 B.3米 C.4米 D.5米
二、填空题
10.一条弦AB把圆的 直径分成3和11两 部分,弦 和 直径相交 成300角,则AB的长为 .
11.如图,在⊙O中,AB是弦,OC⊥AB于C.若OA=5,OC=4,则AB的长为 .
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为 .
13.如图,正方形的顶点A、B和正方形的顶点G、H在一个半径为的上,点E、F在线段上,正方形的边长为,则正方形正方形的边长为 .
14.如图,一大型油罐的截面的直径为,油面宽,则油深 m.
15.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为 寸.
三、解答题
16.如图,弦CD垂直于⊙O的直径AB,垂足为P,且CD=2,BP=1,求⊙O的半径.
17.如图,的两条弦,交于点,平分.
(1)求证:.
(2)若,,求的值.
18.如图1是博物馆展出的古代车轮实物,《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸……”据此, 我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为r cm.
作弦AB的垂线OC,D为垂足,则D是AB的中点.其推理的依据是: .
经测量,AB=90cm,CD=15cm,则AD= cm;
用含r的代数式表示OD,OD= cm.
在Rt△OAD中,由勾股定理可列出关于r的方程:
,解得r=75
通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
19.已知是的直径,点在上,点在半径上(不与点,重合).
(1)如图1,若,,求的度数.
(2)如图2,点在线段上(不与,重合),、的延长线分别交于点、,连接,,点是的延长线与的交点,若,,,,求的长.
参考答案:
1.C
2.A
3.C
4.A
5.D
6.A
7.A
8.C
9.A
10..
11.6
12.3 cm
13.
14.8
15.26
16.
17.(2.
18.垂直于弦的直径平分弦;45;;
19.(1)15°(2)
一、单选题
1.如图,是的直径,弦于点E,,,则的长为( )
A.5 B.3 C.2 D.1.5
2.如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( )
A.40° B.45° C.50° D.60°
3.一块圆形宣传标志牌简图如图所示,点,,在上,垂直平分于点,现测得,,则圆形标志牌的半径为( )
A. B. C. D.
4.如图,AB为⊙O的直径,弦CD与AB交于点E.若AC=AE,CE=4,DE=6,则的值为( )
A. B. C. D.
5.往直径为的圆柱形容器内装入一些水以后,截面如图所示,若水的最大深度为,则水面的宽度为( )
A. B. C. D.
6.如图,矩形的顶点,在半径为5的上,,当点在上运动时,点也随之运动,则矩形的对角线的最小值为( ).
A. B. C. D.
7.如图,的直径为4,弦AB垂直平分半径OC,则四边形OACB的周长为( )
A.8 B.12 C.16 D.20
8.如图,AB是的直径,点B是弧CD的中点,AB交弦CD于E,且,,则( )
A.2 B.3 C.4 D.5
9.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心为圆心.5米为半径的圆,且圆心在水面上方,若圆被水面截得的弦长为8米,则筒车工作时,盛水桶在水面以下的最大深度为( )
A.2米 B.3米 C.4米 D.5米
二、填空题
10.一条弦AB把圆的 直径分成3和11两 部分,弦 和 直径相交 成300角,则AB的长为 .
11.如图,在⊙O中,AB是弦,OC⊥AB于C.若OA=5,OC=4,则AB的长为 .
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为 .
13.如图,正方形的顶点A、B和正方形的顶点G、H在一个半径为的上,点E、F在线段上,正方形的边长为,则正方形正方形的边长为 .
14.如图,一大型油罐的截面的直径为,油面宽,则油深 m.
15.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为 寸.
三、解答题
16.如图,弦CD垂直于⊙O的直径AB,垂足为P,且CD=2,BP=1,求⊙O的半径.
17.如图,的两条弦,交于点,平分.
(1)求证:.
(2)若,,求的值.
18.如图1是博物馆展出的古代车轮实物,《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸……”据此, 我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A、B两点,设所在圆的圆心为O,半径为r cm.
作弦AB的垂线OC,D为垂足,则D是AB的中点.其推理的依据是: .
经测量,AB=90cm,CD=15cm,则AD= cm;
用含r的代数式表示OD,OD= cm.
在Rt△OAD中,由勾股定理可列出关于r的方程:
,解得r=75
通过单位换算,得到车轮直径约为六尺六寸,可验证此车轮为兵车之轮.
19.已知是的直径,点在上,点在半径上(不与点,重合).
(1)如图1,若,,求的度数.
(2)如图2,点在线段上(不与,重合),、的延长线分别交于点、,连接,,点是的延长线与的交点,若,,,,求的长.
参考答案:
1.C
2.A
3.C
4.A
5.D
6.A
7.A
8.C
9.A
10..
11.6
12.3 cm
13.
14.8
15.26
16.
17.(2.
18.垂直于弦的直径平分弦;45;;
19.(1)15°(2)
同课章节目录
