22.2 二次函数与一元二次方程 同步练习(无答案) 2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 22.2 二次函数与一元二次方程 同步练习(无答案) 2023—2024学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 259.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 00:00:00 | ||
图片预览


文档简介
人教版九年级上22.2 二次函数与一元二次方程
一、选择题
1. 若三个方程的正根分别记为,则下列判断正确的是( )
A. B. C. D.
2. 抛物线与x轴的一个交点坐标是,则另一个交点坐标是( )
A. B. C. D.
3. 二次函数的图像如图所示,下列结论:①,②,③,④.其中正确的是( )
A.①④ B.②③ C.①③④ D.①②③④
4. 二次函数的图象与轴交于两点,则的值是( )
A. B. C. D.
5. 如图为抛物线的一部分,其对称轴为直线,若其与x轴的一交点为,则由图象可知,不等式的解集是( )
A. B. C.或 D.
6. 二次函数的图象如图所示,在以下结论:①;②;③;④.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
7. 函数的图像与x轴有交点,则k的取值范围是( )
A. B.且 C. D.且
8. 二次函数的图象如图所示,下列说法正确的是( )
A., B.
C. D.时,不等式一定成立
9. 已知二次函数与轴的一个交点为,其部分图像如图所示,有下列5个结论:①;②;③;④;⑤,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
10. 如图,抛物线与x轴的一个交点坐标为,抛物线的对称轴为直线,下列结论:①;②;③当时,x的取值范围是;④点,都在抛物线上,则有
.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
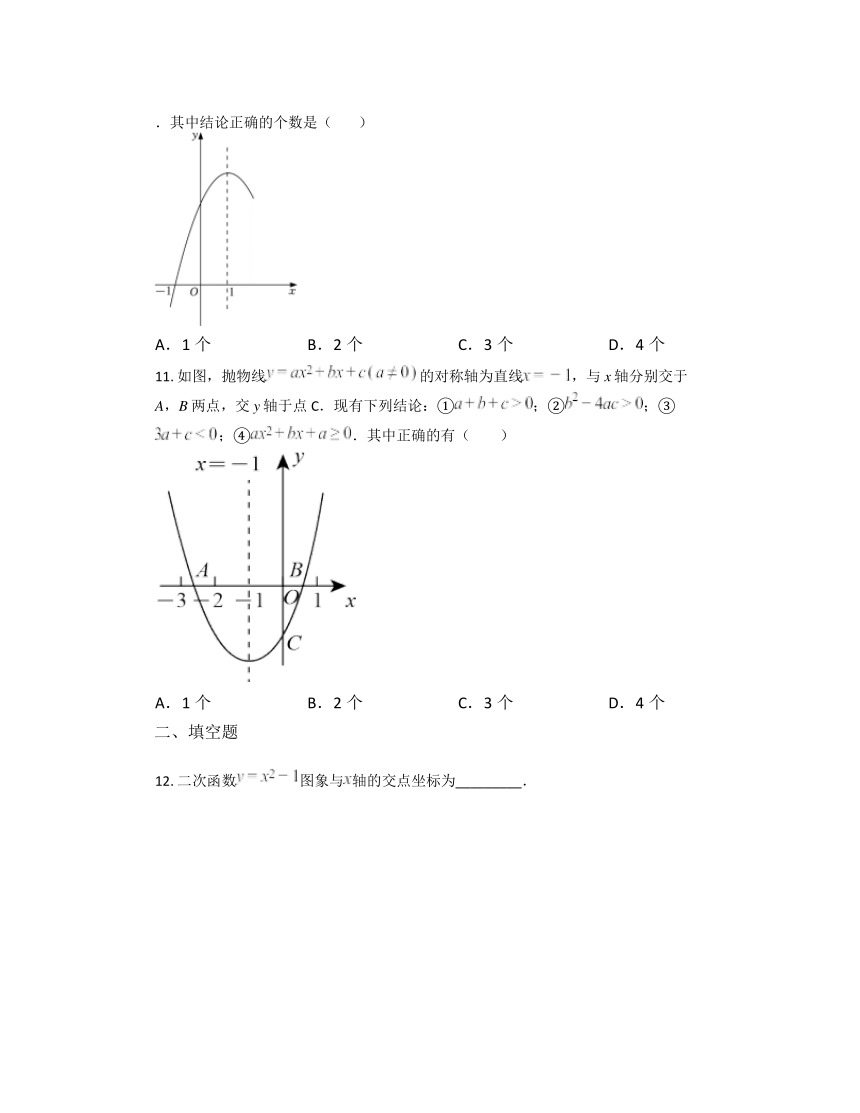
11. 如图,抛物线的对称轴为直线,与x轴分别交于A,B两点,交y轴于点C.现有下列结论:①;②;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
12. 二次函数图象与轴的交点坐标为_________.
13. 二次函数的图象如图所示,则三个代数式①abc,②,③中,值为正数的有______.(填序号)
14. 如图,已知抛物线的图象与轴交于、两点,其中点坐标,对称轴为,则一元二次方程的解为__________.
15. 二次函数(a,b,c为常数)中的x与y的部分对应值如下表:
x -1.4 0 1 2.4
y -1.4 2.4 5 2.4
①;
②当时,y的值随x值的增大而减小;
③是方程的一个根;
④当时,.
以上结论正确的是______(填序号).
三、解答题
16. 画出函数的图象,利用图象回答:
(1)方程的解是什么?
(2)取什么值时,函数值大于0;
(3)取什么值时,函数值小于0.
17. 已知二次函数.
(1)求此函数图象的对称轴和顶点坐标:
(2)画出此函数的图象(不需要列表);
(3)若点和都在此函数的图象上,且,结合函数图象,直接写出m的取值范围.
18. 已知二次函数(m为常数).
(1)求证:不论m为何值该函数图像与x轴必有公共点;
(2)求证:不论m为何值,该函数图像的顶点都在函数的图像上.
(3)已知点,在二次函数图像上,若,则m的取值范围是______.
19. 如图,抛物线与x轴交两点(A点在B点左侧),直线与抛物线交于两点,其中C点的横坐标为.
(1)求两点的坐标;
(2)求直线的函数表达式;
(3)若P是线段上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段长度的最大值.
20. 请阅读下列解题过程;解一元二次不等式;.
解;设,解得;,.
则抛物线与轴的交点坐标为和.
画出二次函数的大致图象(如图所示).
由图象可知;当时函数图象位于轴下方,
此时,即.
所以一元二次不等式的解集为;.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题;
(1)用类似的方法解一元二次不等式;.
(2)某“数学兴趣小组”根据以上的经验,对函数
的图象和性质进行了探究,探究过程如下;
①列表;与的几组对应值如表,其中______.
… 0 1 2 3 4 …
… 5 0 0 1 0 …
②如图,在直角坐标系中画出了函数的部分图象,用描点法将这个图象补画完整.
③结合函数图象,解决下列问题;不等式的解集为;______.
一、选择题
1. 若三个方程的正根分别记为,则下列判断正确的是( )
A. B. C. D.
2. 抛物线与x轴的一个交点坐标是,则另一个交点坐标是( )
A. B. C. D.
3. 二次函数的图像如图所示,下列结论:①,②,③,④.其中正确的是( )
A.①④ B.②③ C.①③④ D.①②③④
4. 二次函数的图象与轴交于两点,则的值是( )
A. B. C. D.
5. 如图为抛物线的一部分,其对称轴为直线,若其与x轴的一交点为,则由图象可知,不等式的解集是( )
A. B. C.或 D.
6. 二次函数的图象如图所示,在以下结论:①;②;③;④.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
7. 函数的图像与x轴有交点,则k的取值范围是( )
A. B.且 C. D.且
8. 二次函数的图象如图所示,下列说法正确的是( )
A., B.
C. D.时,不等式一定成立
9. 已知二次函数与轴的一个交点为,其部分图像如图所示,有下列5个结论:①;②;③;④;⑤,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
10. 如图,抛物线与x轴的一个交点坐标为,抛物线的对称轴为直线,下列结论:①;②;③当时,x的取值范围是;④点,都在抛物线上,则有
.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
11. 如图,抛物线的对称轴为直线,与x轴分别交于A,B两点,交y轴于点C.现有下列结论:①;②;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
12. 二次函数图象与轴的交点坐标为_________.
13. 二次函数的图象如图所示,则三个代数式①abc,②,③中,值为正数的有______.(填序号)
14. 如图,已知抛物线的图象与轴交于、两点,其中点坐标,对称轴为,则一元二次方程的解为__________.
15. 二次函数(a,b,c为常数)中的x与y的部分对应值如下表:
x -1.4 0 1 2.4
y -1.4 2.4 5 2.4
①;
②当时,y的值随x值的增大而减小;
③是方程的一个根;
④当时,.
以上结论正确的是______(填序号).
三、解答题
16. 画出函数的图象,利用图象回答:
(1)方程的解是什么?
(2)取什么值时,函数值大于0;
(3)取什么值时,函数值小于0.
17. 已知二次函数.
(1)求此函数图象的对称轴和顶点坐标:
(2)画出此函数的图象(不需要列表);
(3)若点和都在此函数的图象上,且,结合函数图象,直接写出m的取值范围.
18. 已知二次函数(m为常数).
(1)求证:不论m为何值该函数图像与x轴必有公共点;
(2)求证:不论m为何值,该函数图像的顶点都在函数的图像上.
(3)已知点,在二次函数图像上,若,则m的取值范围是______.
19. 如图,抛物线与x轴交两点(A点在B点左侧),直线与抛物线交于两点,其中C点的横坐标为.
(1)求两点的坐标;
(2)求直线的函数表达式;
(3)若P是线段上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段长度的最大值.
20. 请阅读下列解题过程;解一元二次不等式;.
解;设,解得;,.
则抛物线与轴的交点坐标为和.
画出二次函数的大致图象(如图所示).
由图象可知;当时函数图象位于轴下方,
此时,即.
所以一元二次不等式的解集为;.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题;
(1)用类似的方法解一元二次不等式;.
(2)某“数学兴趣小组”根据以上的经验,对函数
的图象和性质进行了探究,探究过程如下;
①列表;与的几组对应值如表,其中______.
… 0 1 2 3 4 …
… 5 0 0 1 0 …
②如图,在直角坐标系中画出了函数的部分图象,用描点法将这个图象补画完整.
③结合函数图象,解决下列问题;不等式的解集为;______.
同课章节目录
