第三章 一元一次方程 单元检测(含答案) 2023—2024学年人教版数学七年级上册
文档属性
| 名称 | 第三章 一元一次方程 单元检测(含答案) 2023—2024学年人教版数学七年级上册 |
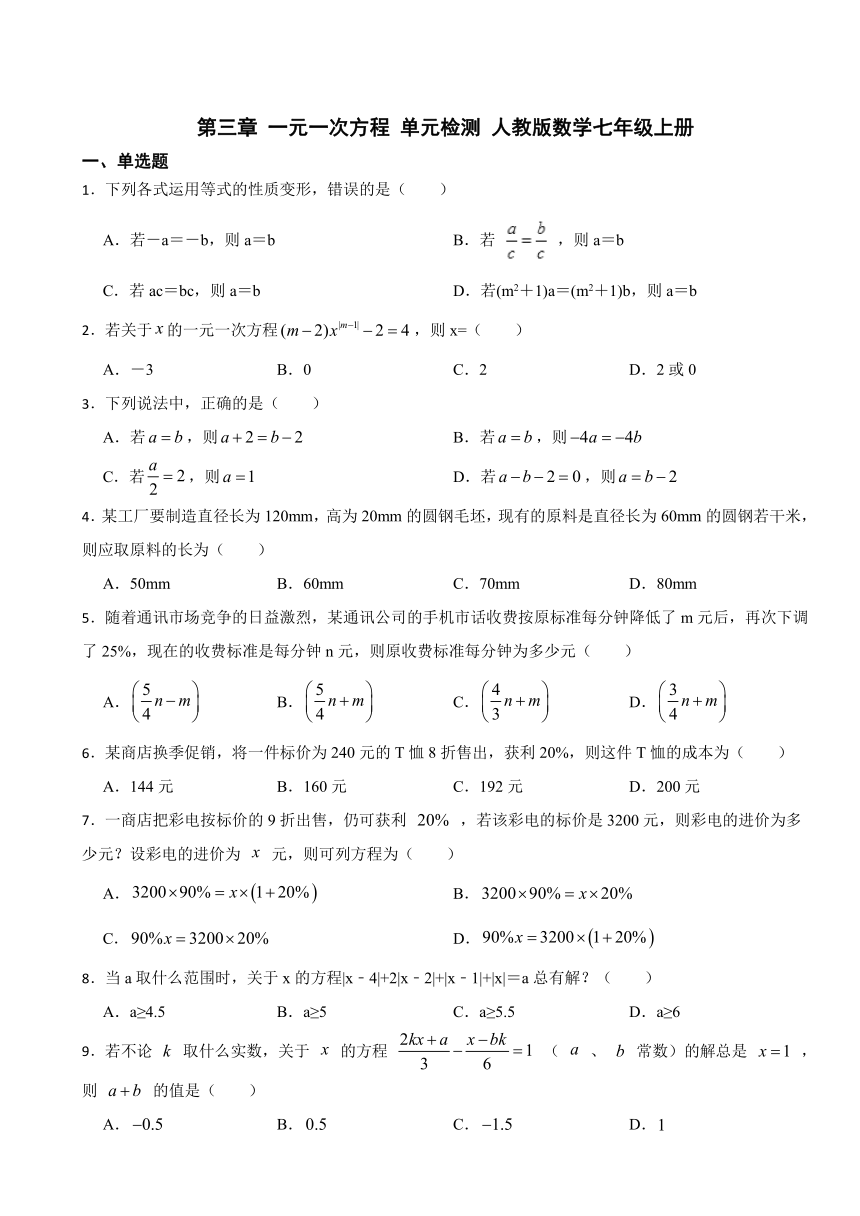
|
|
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-12 00:00:00 | ||
图片预览
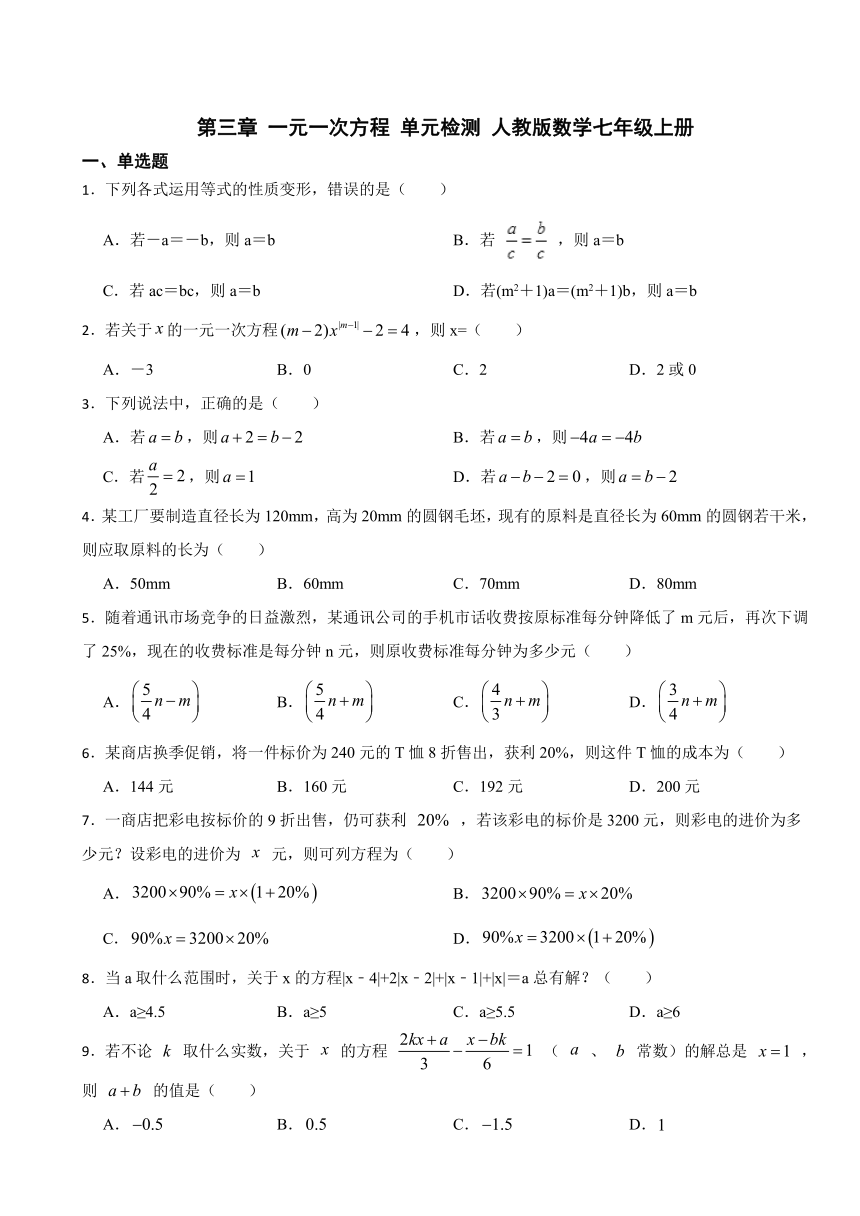




文档简介
第三章 一元一次方程 单元检测 人教版数学七年级上册
一、单选题
1.下列各式运用等式的性质变形,错误的是( )
A.若-a=-b,则a=b B.若 ,则a=b
C.若ac=bc,则a=b D.若(m2+1)a=(m2+1)b,则a=b
2.若关于的一元一次方程,则x=( )
A.-3 B.0 C.2 D.2或0
3.下列说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.某工厂要制造直径长为120mm,高为20mm的圆钢毛坯,现有的原料是直径长为60mm的圆钢若干米,则应取原料的长为( )
A.50mm B.60mm C.70mm D.80mm
5.随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费按原标准每分钟降低了m元后,再次下调了25%,现在的收费标准是每分钟n元,则原收费标准每分钟为多少元( )
A. B. C. D.
6.某商店换季促销,将一件标价为240元的T恤8折售出,获利20%,则这件T恤的成本为( )
A.144元 B.160元 C.192元 D.200元
7.一商店把彩电按标价的9折出售,仍可获利 ,若该彩电的标价是3200元,则彩电的进价为多少元?设彩电的进价为 元,则可列方程为( )
A. B.
C. D.
8.当a取什么范围时,关于x的方程|x﹣4|+2|x﹣2|+|x﹣1|+|x|=a总有解?( )
A.a≥4.5 B.a≥5 C.a≥5.5 D.a≥6
9.若不论 取什么实数,关于 的方程 ( 、 常数)的解总是 ,则 的值是( )
A. B. C. D.
10.下列结论:①几个有理数相乘,若其中负因数有奇数个,则积为负;②两个三次多项式的和一定是三次多项式;③若xyz<0,则 + + + 的值为0或﹣4;④若a,b互为相反数,则 =﹣1;⑤若x=y,则 = .其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.当x为 时, 的值为﹣1.
12.已知关于x的方程(k﹣1)x|k|﹣1=0是一元一次方程,则k的值为 .
13.今年福安白云山千古冰臼群迎来旅游高峰,前三天的游客人数共计约5.1万人,其中第一天的游客人数是1.2万人,假设每天游客增加的百分率相同,且设为,则根据题意可列方程为 .
14.已知数轴上三点M,O,N对应的数分别是-1,0,3,点P为数轴上任意点,其对应的数为x.如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时P点到点M、点N的距离相等,则t的值为 .
15.已知关于x的一元一次方程 +5=2019x+m的解为x=2018,那么关于y的一元一次方程 ﹣5=2019(5﹣y)﹣m的解为 .
三、计算题
16.解下列方程
(1)
(2)
17.
(1)2(x﹣2)﹣3(4x﹣1)=9(1﹣x);
(2) .
四、解答题
18.应用题:某商场进了一批豆浆机,按进价的180%标价,春节期间,为了能吸引消费者,打7折销售,此时每台豆浆机仍可获利52元,请问每台豆浆机的进价是多少元?
19.列方程解应用题:
某车间有84名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知1个大齿轮和2个小齿轮配成一套,问分别安排多少名工人加工大小齿轮,才能刚好配套?一共可以配成多少套?
20.学校准备添置一批课桌椅,原计划订购60套,每套100元.店方表示:如果多购可以优惠.结果校方购了72套,每套减价3元,但商店获得同样多的利润.求每套课桌椅的成本.
21.一项工程,甲队单独完成需30天,乙队单独完成需45天,现甲队先单独做20天,之后两队合作.
(1)甲.乙合作多少天才能把该工程完成?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在40天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
22.某服装商场购进一批T恤,每件进价40元,出于营销考虑,要求每件售价不得低于40元且不得高于60元,在销售过程中发现该T恤每周的销售量 (件)与每件售价 (元)之间满足一次函数关系:当销售单价为44元时,销量是72件,当销售单价为48元时,销售量为64件.
(1)请直接写出 与 的函数关系式;
(2)当商场每周销售这种T恤获得350元的利润时,每件的销售单价是多少元?
(3)设该商场每周销售这种T恤所获得的利润为 元,将该T恤销售单价定为多少元时,才能使商场销售该T恤所获利润最大?最大利润是多少?
答案解析部分
1.【答案】C
【解析】【解答】A、等式-a=-b两边同时乘以(-1),得 ,即a=b. 故A不符合题意.
B、等式 两边同时乘以c,得 ,即a=b. 故B不符合题意.
C、当c≠0时,等式ac=bc两边同时除以c,得 ,即a=b;当c=0时,根据等式的性质不能进行类似的变形. 故C符合题意.
D、因为 ,所以m2+1>0,故m2+1≠0. 因此,等式(m2+1)a=(m2+1)b两边同时除以(m2+1),得 ,即a=b. 故D不符合题意.
故答案为:C.
【分析】等式的基本性质1:等式两边同时加减同一个代数式,所得结果仍是等式;等式性质2:等式两边同时乘同一个数(或除以同一个不为0的数),所得结果仍是等式。所以A.C两项容易得出结论,D项中m2+1>0,所以也正确;而C项若c为0,则不成立。
2.【答案】A
【解析】【解答】解:由题意可知:,
解得:.
把代入原方程得:
.
故答案为:A.
【分析】根据一元一次方程的定义可得,求出m的值,再将m的值代入原方程,最后计算即可。
3.【答案】B
【解析】【解答】解:A. 若,根据等式的性质一,两边同时加2,则,不符合题意;
B. 若,根据等式的性质二,两边同时乘-4,则,符合题意;
C. 若,根据等式的性质二,两边同时乘4,则,不符合题意;
D. 若,根据等式的性质一,两边同时加,则,不符合题意;
故答案为:B.
【分析】根据等式的基本性质对每个选项一一判断即可。
4.【答案】D
【解析】【解答】设需要直径为60mm的圆钢xmm长,依题意有
π×(60÷2)2x=π×(120÷2)2×20,
解得x=80.
所以,需要直径为60mm的圆钢80mm长.
故答案为:D.
【分析】可设需要直径为60mm的圆钢xmm长,根据等量关系:直径为120mm,高为20mm的圆柱体积=直径为60mm的圆钢体积,列出方程即可求解.
5.【答案】C
【解析】【解答】解:设原收费标准每分钟为x元,
由题意得, ,
解得,
故答案为:C.
【分析】设原收费标准每分钟为x元,则根据题意,以现在的收费标准为等量关系,列出等式,表示出原收费标准即可.
6.【答案】B
【解析】【解答】解:设成本为x元,则获利为20%x元,售价为0.8×240元,
由题意得:x+20%x=0.8×240,
解得:x=160.
即成本为160元.
故答案为:B.
【分析】根据题意求出x+20%x=0.8×240,再解方程即可。
7.【答案】A
【解析】【解答】解:设彩电的进价为 x 元,根据题意得:
.
故答案为:A.
【分析】根据 一商店把彩电按标价的9折出售,仍可获利 ,该彩电的标价是3200元,列方程求解即可。
8.【答案】B
【解析】【解答】解:令y=|x﹣4|+2|x﹣2|+|x﹣1|+|x|,
当x≥4时,y=5x﹣9≥11,
当2<x<4时,y=3x﹣1,
∴5<y<11;
当1≤x≤2时,y=﹣x+7,
∴5≤y≤6;
当0<x<1时,y=﹣3x+9,
∴6<y<9;
当x≤0时,y=﹣5x+9,
∴y≥9;
综上所述,y≥5,
∴a≥5时等式恒有解.
故答案为:B.
【分析】令y=|x-4|+2|x-2|+|x-1|+|x|,根据x的范围分情况去掉绝对值符号,可求得y≥5,再结合题意即可确定a的范围.
9.【答案】A
【解析】【解答】解:∵关于x的方程 的解总是
∴
∴
∴
∴
解得:
∴
故答案为:A.
【分析】将x=1代入方程中可得,根据方程解总是 ,可知该方程的解与k的值无关,故可得字母k的系数应该等于0,据此推出4+b=0,7-2a=0,据此解答即可.
10.【答案】B
【解析】【解答】解:①几个有理数相乘,如果其中一个因数为0,积为0,所以①错误;
②两个三次多项式的和不一定是三次多项式,所以②错误;
③∵xyz<0,
∴分两种情况:一种是两正一负,设x>0,y>0,z<0,
则原式=1+1-1-1=0;
一种是三个数都为负数,
则原式=-1-1-1-1=-4,所以③正确;
④∵0的相反数是0, 无意义,∴若a,b互为相反数,则 =﹣1不正确,所以④错误;
⑤两个分式的分子和分母都相等,则两个分式相等,所以⑤正确.
故答案为:B.
【分析】①几个有理数相乘,如果其中一个因数为0,积为0,无论负因数的个数是奇数个还是偶数个;②两个三次多项式的和不一定是三次多项式,也可能三次项合并后为0;③x、y、z可能两个正数一个负数,也可能都是分数,分两种情况求解即可得结论;④根据互为相反数的两个数商为-1但0的相反数为0,即可判断;⑤两个分式的分子和分母都相同,分式的值也相同即可判断.
11.【答案】﹣
【解析】【解答】根据题意可得:
去分母,得
移项,得
合并同类项,得
系数化为1,得
故答案为:
【分析】由题意可得关于x的方程,然后根据一元一次方程的解题步骤“去分母、去括号、移项、合并同类项、系数化为1”可求解.
12.【答案】﹣1
【解析】【解答】解:根据题意得:|k=1,且k-1≠0,计算得出:k=-1,
因此, 本题符合题意答案是:-1.
【分析】根据一元一次方程定义可得:|k|= 1,且k﹣1≠0,再解即可.
13.【答案】
【解析】【解答】解:假设每天游客增加的百分率相同,且设为,
第二天的游客人数为1.2(1+x),
第三天的游客人数为1.2(1+x)2,
则根据题意可列方程为1.2+1.2(1+x)+1.2(1+x)2=5.1.
故答案为:1.2+1.2(1+x)+1.2(1+x)2=5.1.
【分析】设每天游客增加的百分率为,则可得出第二天的游客人数为1.2(1+x),第三天的游客人数为1.2(1+x)2,再根据前三天的游客人数之和约5.1万人列出方程,即可解答.
14.【答案】 或4
【解析】【解答】设运动t分钟时,点P到点M,点N的距离相等,即PM=PN.
点P对应的数是-t,点M对应的数是-1-2t,点N对应的数是3-3t.
①当点M和点N在点P同侧时,点M和点N重合,
所以-1-2t=3-3t,解得t=4,符合题意.
②当点M和点N在点P异侧时,点M位于点P的左侧,点N位于点P的右侧(因为三个点都向左运动,出发时点M在点P左侧,且点M运动的速度大于点P的速度,所以点M永远位于点P的左侧),
故PM=-t-(-1-2t)=t+1.PN=(3-3t)-(-t)=3-2t.
所以t+1=3-2t,解得t= ,符合题意.
综上所述,t的值为 或4.
【分析】设运动t分钟时,点P到点M,点N的距离相等,即PM=PN.点P对应的数是-t,点M对应的数是-1-2t,点N对应的数是3-3t.分两种情况:①当点M和点N在点P同侧时,②当点M和点N在点P异侧时,据此由PM=PN分别列出方程,解之即可.
15.【答案】2023
【解析】【解答】解:根据题意得:
方程 可整理得: ,
则该方程的解为x=2018,
方程 可整理得: ,
令n=5﹣y,
则原方程可整理得: ,
则n=﹣2018,
即5﹣y=﹣2018,
解得:y=2023,
故答案为:2023.
【分析】将方程整理可得,则该方程的解为x=2018;将关于y的方程整理为,令n=5﹣y,可得出,从而可得5﹣y=n﹣2018,求出y值即可.
16.【答案】(1)解:
(2)解:
【解析】【分析】(1)按照以下步骤计算:移项(注意改变符号);合并同类项;系数化为1.(2)按照下面的步骤计算:①两边同时除以各分母的最小公倍数6去分母;②根据乘法的分配律去括号(不要漏乘);③移项(注意改变符号);④合并同类项;⑤系数化为1.
17.【答案】(1)解:去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
(2)解:去分母,得:
去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
【解析】【分析】(1)依次去括号,移项,合并同类项,系数化为1,即可得到答案;
(2)依次去分母,去括号,移项,合并同类项,系数化为1,即可得到答案;
18.【答案】解:设每台豆浆机的进价是x元
由题意得:
解得:
答:每台豆浆机的进价是200元
【解析】【分析】设每台豆浆机的进价是x元,根据:售价-进价=利润,列出方程,求解即可.
19.【答案】解:设每天加工的大齿轮的有x人,则每天加工的小齿轮的有(84-x)人,根据题意可得;
2×16x=10(84-x),
解得:x=20,
则84-20=64(人).
配成的套数为:20×16=320(套).
答:每天应安排20人加工大齿轮,安排64人加工小齿轮,才能刚好配套;一共可以配成320套.
【解析】【分析】首先设每天加工大齿轮的有x人,则每天加工小齿轮的有(84-x)人,再利用1个大齿轮与2个小齿轮刚好配成一套得出等式求出答案.
20.【答案】解:设每套课桌椅的成本x元.
则:60×(100﹣x)=72×(100﹣3﹣x).
解之得:x=82.
答:每套课桌椅成本82元
【解析】【分析】设每套课桌椅的成本x元.原计划订购60套,每套100元,所获得的利润为60×(100﹣x),校方购了72套,每套减价3元,所获得的利润为72×(100﹣3﹣x).由商店获得同样多的利润得出方程求解即可。
21.【答案】(1)解:设甲、乙合作x天才能把该工程完成,
根据题意得(x+20)+x=1,
解得x=6,
答:甲、乙合作6天才能把该工程完成.
(2)解:∵45天大于40天,所以不能由乙队单独完成.
若由甲队单独完成,则需3.5×30=105(万元);
设由甲、乙全程合作完成需要m天,则:m+ m=1,
解得m=18,
35×18+2×18=99(万元),
99万元<105万元,
答:由甲、乙两队全程合作完成该工程省钱.
【解析】【分析】(1)根据等量关系式“ 甲队先单独做20天的工作量+甲乙合作x天的工作量=总工作量 ”,列方程,即可求出x的值,从而求出合作天数;
(2)先根据计划完成的天数判断乙不能单独完成,从而求出甲单独完成的费用;其次讨论合作完成时,设完成天数m,列一元一次方程,求出m的值,即可求出甲乙合作完成费用,与甲单独完成合作费用比较即可求互甲乙合作省钱.
22.【答案】(1)解:设y=kx+b,
把(44,72)与(48,64)代入得:
解得: ,
则y=-2x+160
(2)解:设当饰品店每周销售这种饰品获得350元的利润时,每件饰品的销售单价是x元,
根据题意得:(x-40)y=350,即(x-40)(-2x+160)=350,
解得:x1=45,x2=75(不合题意舍去),
答:每件饰品的销售单价是45元
(3)解:
=
∵40≤ ≤60,
∴ 当 时, 最大,最大利润为800元。
答:每件产品的销售价为60时,商场销售该T恤获最大利润为800元。
【解析】【分析】(1)将售价与销售量的值代入一次函数,可得出一次函数值。
(2)列出利润=(售价-进价)×销售量,得出满足此利润的售价。
(3)列出总利润=(售价-进价)×销售量,销售量由第(1)问的函数关系式表示,可得出获得最大利润的销售价。
一、单选题
1.下列各式运用等式的性质变形,错误的是( )
A.若-a=-b,则a=b B.若 ,则a=b
C.若ac=bc,则a=b D.若(m2+1)a=(m2+1)b,则a=b
2.若关于的一元一次方程,则x=( )
A.-3 B.0 C.2 D.2或0
3.下列说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.某工厂要制造直径长为120mm,高为20mm的圆钢毛坯,现有的原料是直径长为60mm的圆钢若干米,则应取原料的长为( )
A.50mm B.60mm C.70mm D.80mm
5.随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费按原标准每分钟降低了m元后,再次下调了25%,现在的收费标准是每分钟n元,则原收费标准每分钟为多少元( )
A. B. C. D.
6.某商店换季促销,将一件标价为240元的T恤8折售出,获利20%,则这件T恤的成本为( )
A.144元 B.160元 C.192元 D.200元
7.一商店把彩电按标价的9折出售,仍可获利 ,若该彩电的标价是3200元,则彩电的进价为多少元?设彩电的进价为 元,则可列方程为( )
A. B.
C. D.
8.当a取什么范围时,关于x的方程|x﹣4|+2|x﹣2|+|x﹣1|+|x|=a总有解?( )
A.a≥4.5 B.a≥5 C.a≥5.5 D.a≥6
9.若不论 取什么实数,关于 的方程 ( 、 常数)的解总是 ,则 的值是( )
A. B. C. D.
10.下列结论:①几个有理数相乘,若其中负因数有奇数个,则积为负;②两个三次多项式的和一定是三次多项式;③若xyz<0,则 + + + 的值为0或﹣4;④若a,b互为相反数,则 =﹣1;⑤若x=y,则 = .其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.当x为 时, 的值为﹣1.
12.已知关于x的方程(k﹣1)x|k|﹣1=0是一元一次方程,则k的值为 .
13.今年福安白云山千古冰臼群迎来旅游高峰,前三天的游客人数共计约5.1万人,其中第一天的游客人数是1.2万人,假设每天游客增加的百分率相同,且设为,则根据题意可列方程为 .
14.已知数轴上三点M,O,N对应的数分别是-1,0,3,点P为数轴上任意点,其对应的数为x.如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时P点到点M、点N的距离相等,则t的值为 .
15.已知关于x的一元一次方程 +5=2019x+m的解为x=2018,那么关于y的一元一次方程 ﹣5=2019(5﹣y)﹣m的解为 .
三、计算题
16.解下列方程
(1)
(2)
17.
(1)2(x﹣2)﹣3(4x﹣1)=9(1﹣x);
(2) .
四、解答题
18.应用题:某商场进了一批豆浆机,按进价的180%标价,春节期间,为了能吸引消费者,打7折销售,此时每台豆浆机仍可获利52元,请问每台豆浆机的进价是多少元?
19.列方程解应用题:
某车间有84名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知1个大齿轮和2个小齿轮配成一套,问分别安排多少名工人加工大小齿轮,才能刚好配套?一共可以配成多少套?
20.学校准备添置一批课桌椅,原计划订购60套,每套100元.店方表示:如果多购可以优惠.结果校方购了72套,每套减价3元,但商店获得同样多的利润.求每套课桌椅的成本.
21.一项工程,甲队单独完成需30天,乙队单独完成需45天,现甲队先单独做20天,之后两队合作.
(1)甲.乙合作多少天才能把该工程完成?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在40天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
22.某服装商场购进一批T恤,每件进价40元,出于营销考虑,要求每件售价不得低于40元且不得高于60元,在销售过程中发现该T恤每周的销售量 (件)与每件售价 (元)之间满足一次函数关系:当销售单价为44元时,销量是72件,当销售单价为48元时,销售量为64件.
(1)请直接写出 与 的函数关系式;
(2)当商场每周销售这种T恤获得350元的利润时,每件的销售单价是多少元?
(3)设该商场每周销售这种T恤所获得的利润为 元,将该T恤销售单价定为多少元时,才能使商场销售该T恤所获利润最大?最大利润是多少?
答案解析部分
1.【答案】C
【解析】【解答】A、等式-a=-b两边同时乘以(-1),得 ,即a=b. 故A不符合题意.
B、等式 两边同时乘以c,得 ,即a=b. 故B不符合题意.
C、当c≠0时,等式ac=bc两边同时除以c,得 ,即a=b;当c=0时,根据等式的性质不能进行类似的变形. 故C符合题意.
D、因为 ,所以m2+1>0,故m2+1≠0. 因此,等式(m2+1)a=(m2+1)b两边同时除以(m2+1),得 ,即a=b. 故D不符合题意.
故答案为:C.
【分析】等式的基本性质1:等式两边同时加减同一个代数式,所得结果仍是等式;等式性质2:等式两边同时乘同一个数(或除以同一个不为0的数),所得结果仍是等式。所以A.C两项容易得出结论,D项中m2+1>0,所以也正确;而C项若c为0,则不成立。
2.【答案】A
【解析】【解答】解:由题意可知:,
解得:.
把代入原方程得:
.
故答案为:A.
【分析】根据一元一次方程的定义可得,求出m的值,再将m的值代入原方程,最后计算即可。
3.【答案】B
【解析】【解答】解:A. 若,根据等式的性质一,两边同时加2,则,不符合题意;
B. 若,根据等式的性质二,两边同时乘-4,则,符合题意;
C. 若,根据等式的性质二,两边同时乘4,则,不符合题意;
D. 若,根据等式的性质一,两边同时加,则,不符合题意;
故答案为:B.
【分析】根据等式的基本性质对每个选项一一判断即可。
4.【答案】D
【解析】【解答】设需要直径为60mm的圆钢xmm长,依题意有
π×(60÷2)2x=π×(120÷2)2×20,
解得x=80.
所以,需要直径为60mm的圆钢80mm长.
故答案为:D.
【分析】可设需要直径为60mm的圆钢xmm长,根据等量关系:直径为120mm,高为20mm的圆柱体积=直径为60mm的圆钢体积,列出方程即可求解.
5.【答案】C
【解析】【解答】解:设原收费标准每分钟为x元,
由题意得, ,
解得,
故答案为:C.
【分析】设原收费标准每分钟为x元,则根据题意,以现在的收费标准为等量关系,列出等式,表示出原收费标准即可.
6.【答案】B
【解析】【解答】解:设成本为x元,则获利为20%x元,售价为0.8×240元,
由题意得:x+20%x=0.8×240,
解得:x=160.
即成本为160元.
故答案为:B.
【分析】根据题意求出x+20%x=0.8×240,再解方程即可。
7.【答案】A
【解析】【解答】解:设彩电的进价为 x 元,根据题意得:
.
故答案为:A.
【分析】根据 一商店把彩电按标价的9折出售,仍可获利 ,该彩电的标价是3200元,列方程求解即可。
8.【答案】B
【解析】【解答】解:令y=|x﹣4|+2|x﹣2|+|x﹣1|+|x|,
当x≥4时,y=5x﹣9≥11,
当2<x<4时,y=3x﹣1,
∴5<y<11;
当1≤x≤2时,y=﹣x+7,
∴5≤y≤6;
当0<x<1时,y=﹣3x+9,
∴6<y<9;
当x≤0时,y=﹣5x+9,
∴y≥9;
综上所述,y≥5,
∴a≥5时等式恒有解.
故答案为:B.
【分析】令y=|x-4|+2|x-2|+|x-1|+|x|,根据x的范围分情况去掉绝对值符号,可求得y≥5,再结合题意即可确定a的范围.
9.【答案】A
【解析】【解答】解:∵关于x的方程 的解总是
∴
∴
∴
∴
解得:
∴
故答案为:A.
【分析】将x=1代入方程中可得,根据方程解总是 ,可知该方程的解与k的值无关,故可得字母k的系数应该等于0,据此推出4+b=0,7-2a=0,据此解答即可.
10.【答案】B
【解析】【解答】解:①几个有理数相乘,如果其中一个因数为0,积为0,所以①错误;
②两个三次多项式的和不一定是三次多项式,所以②错误;
③∵xyz<0,
∴分两种情况:一种是两正一负,设x>0,y>0,z<0,
则原式=1+1-1-1=0;
一种是三个数都为负数,
则原式=-1-1-1-1=-4,所以③正确;
④∵0的相反数是0, 无意义,∴若a,b互为相反数,则 =﹣1不正确,所以④错误;
⑤两个分式的分子和分母都相等,则两个分式相等,所以⑤正确.
故答案为:B.
【分析】①几个有理数相乘,如果其中一个因数为0,积为0,无论负因数的个数是奇数个还是偶数个;②两个三次多项式的和不一定是三次多项式,也可能三次项合并后为0;③x、y、z可能两个正数一个负数,也可能都是分数,分两种情况求解即可得结论;④根据互为相反数的两个数商为-1但0的相反数为0,即可判断;⑤两个分式的分子和分母都相同,分式的值也相同即可判断.
11.【答案】﹣
【解析】【解答】根据题意可得:
去分母,得
移项,得
合并同类项,得
系数化为1,得
故答案为:
【分析】由题意可得关于x的方程,然后根据一元一次方程的解题步骤“去分母、去括号、移项、合并同类项、系数化为1”可求解.
12.【答案】﹣1
【解析】【解答】解:根据题意得:|k=1,且k-1≠0,计算得出:k=-1,
因此, 本题符合题意答案是:-1.
【分析】根据一元一次方程定义可得:|k|= 1,且k﹣1≠0,再解即可.
13.【答案】
【解析】【解答】解:假设每天游客增加的百分率相同,且设为,
第二天的游客人数为1.2(1+x),
第三天的游客人数为1.2(1+x)2,
则根据题意可列方程为1.2+1.2(1+x)+1.2(1+x)2=5.1.
故答案为:1.2+1.2(1+x)+1.2(1+x)2=5.1.
【分析】设每天游客增加的百分率为,则可得出第二天的游客人数为1.2(1+x),第三天的游客人数为1.2(1+x)2,再根据前三天的游客人数之和约5.1万人列出方程,即可解答.
14.【答案】 或4
【解析】【解答】设运动t分钟时,点P到点M,点N的距离相等,即PM=PN.
点P对应的数是-t,点M对应的数是-1-2t,点N对应的数是3-3t.
①当点M和点N在点P同侧时,点M和点N重合,
所以-1-2t=3-3t,解得t=4,符合题意.
②当点M和点N在点P异侧时,点M位于点P的左侧,点N位于点P的右侧(因为三个点都向左运动,出发时点M在点P左侧,且点M运动的速度大于点P的速度,所以点M永远位于点P的左侧),
故PM=-t-(-1-2t)=t+1.PN=(3-3t)-(-t)=3-2t.
所以t+1=3-2t,解得t= ,符合题意.
综上所述,t的值为 或4.
【分析】设运动t分钟时,点P到点M,点N的距离相等,即PM=PN.点P对应的数是-t,点M对应的数是-1-2t,点N对应的数是3-3t.分两种情况:①当点M和点N在点P同侧时,②当点M和点N在点P异侧时,据此由PM=PN分别列出方程,解之即可.
15.【答案】2023
【解析】【解答】解:根据题意得:
方程 可整理得: ,
则该方程的解为x=2018,
方程 可整理得: ,
令n=5﹣y,
则原方程可整理得: ,
则n=﹣2018,
即5﹣y=﹣2018,
解得:y=2023,
故答案为:2023.
【分析】将方程整理可得,则该方程的解为x=2018;将关于y的方程整理为,令n=5﹣y,可得出,从而可得5﹣y=n﹣2018,求出y值即可.
16.【答案】(1)解:
(2)解:
【解析】【分析】(1)按照以下步骤计算:移项(注意改变符号);合并同类项;系数化为1.(2)按照下面的步骤计算:①两边同时除以各分母的最小公倍数6去分母;②根据乘法的分配律去括号(不要漏乘);③移项(注意改变符号);④合并同类项;⑤系数化为1.
17.【答案】(1)解:去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
(2)解:去分母,得:
去括号,得:
移项,得:
合并同类项,得:
系数化为1,得:
【解析】【分析】(1)依次去括号,移项,合并同类项,系数化为1,即可得到答案;
(2)依次去分母,去括号,移项,合并同类项,系数化为1,即可得到答案;
18.【答案】解:设每台豆浆机的进价是x元
由题意得:
解得:
答:每台豆浆机的进价是200元
【解析】【分析】设每台豆浆机的进价是x元,根据:售价-进价=利润,列出方程,求解即可.
19.【答案】解:设每天加工的大齿轮的有x人,则每天加工的小齿轮的有(84-x)人,根据题意可得;
2×16x=10(84-x),
解得:x=20,
则84-20=64(人).
配成的套数为:20×16=320(套).
答:每天应安排20人加工大齿轮,安排64人加工小齿轮,才能刚好配套;一共可以配成320套.
【解析】【分析】首先设每天加工大齿轮的有x人,则每天加工小齿轮的有(84-x)人,再利用1个大齿轮与2个小齿轮刚好配成一套得出等式求出答案.
20.【答案】解:设每套课桌椅的成本x元.
则:60×(100﹣x)=72×(100﹣3﹣x).
解之得:x=82.
答:每套课桌椅成本82元
【解析】【分析】设每套课桌椅的成本x元.原计划订购60套,每套100元,所获得的利润为60×(100﹣x),校方购了72套,每套减价3元,所获得的利润为72×(100﹣3﹣x).由商店获得同样多的利润得出方程求解即可。
21.【答案】(1)解:设甲、乙合作x天才能把该工程完成,
根据题意得(x+20)+x=1,
解得x=6,
答:甲、乙合作6天才能把该工程完成.
(2)解:∵45天大于40天,所以不能由乙队单独完成.
若由甲队单独完成,则需3.5×30=105(万元);
设由甲、乙全程合作完成需要m天,则:m+ m=1,
解得m=18,
35×18+2×18=99(万元),
99万元<105万元,
答:由甲、乙两队全程合作完成该工程省钱.
【解析】【分析】(1)根据等量关系式“ 甲队先单独做20天的工作量+甲乙合作x天的工作量=总工作量 ”,列方程,即可求出x的值,从而求出合作天数;
(2)先根据计划完成的天数判断乙不能单独完成,从而求出甲单独完成的费用;其次讨论合作完成时,设完成天数m,列一元一次方程,求出m的值,即可求出甲乙合作完成费用,与甲单独完成合作费用比较即可求互甲乙合作省钱.
22.【答案】(1)解:设y=kx+b,
把(44,72)与(48,64)代入得:
解得: ,
则y=-2x+160
(2)解:设当饰品店每周销售这种饰品获得350元的利润时,每件饰品的销售单价是x元,
根据题意得:(x-40)y=350,即(x-40)(-2x+160)=350,
解得:x1=45,x2=75(不合题意舍去),
答:每件饰品的销售单价是45元
(3)解:
=
∵40≤ ≤60,
∴ 当 时, 最大,最大利润为800元。
答:每件产品的销售价为60时,商场销售该T恤获最大利润为800元。
【解析】【分析】(1)将售价与销售量的值代入一次函数,可得出一次函数值。
(2)列出利润=(售价-进价)×销售量,得出满足此利润的售价。
(3)列出总利润=(售价-进价)×销售量,销售量由第(1)问的函数关系式表示,可得出获得最大利润的销售价。
