镶嵌
图片预览







文档简介
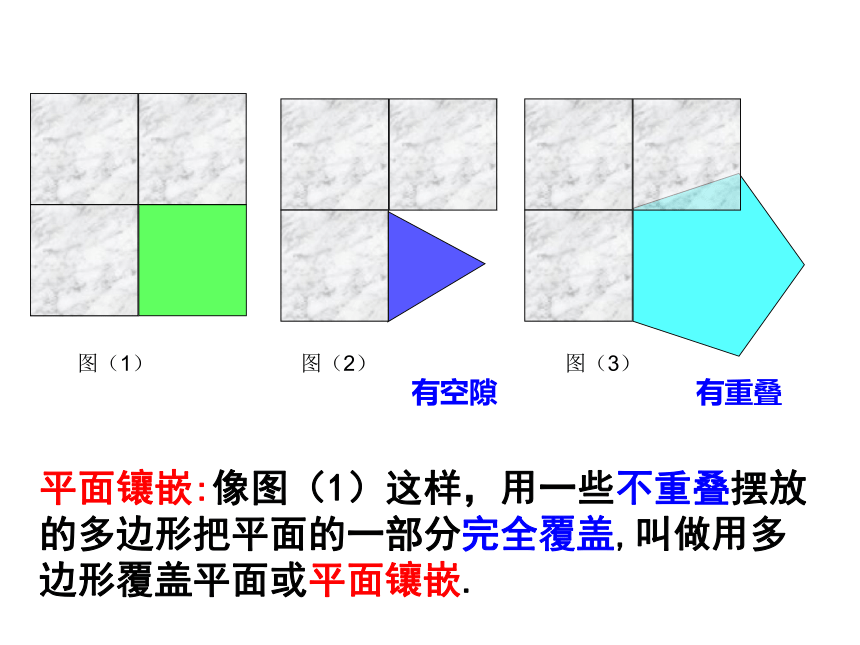
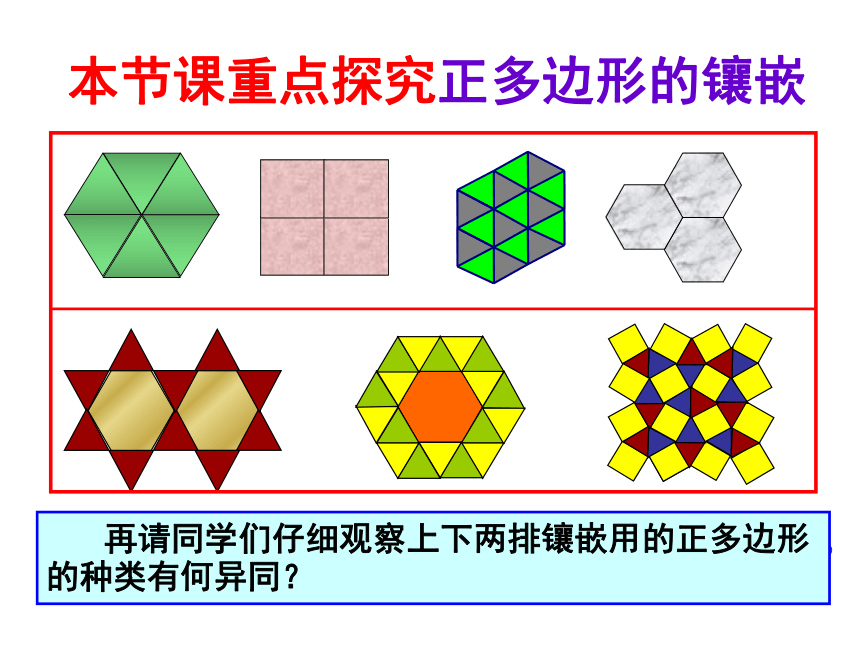
课件27张PPT。镶 嵌(一)镶 嵌(一) —用正多边形镶嵌平面义务教育课程标准实验教科书人教版教材 (七年级下册)课 题 学 习(3)感受生活中的镶嵌图形 你能从中发现什么?有什么感触呢?图(1)图(2)图(3)平面镶嵌:像图(1)这样,用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面或平面镶嵌.有空隙有重叠 请同学们仔细观察,以上用于镶嵌的基本图形有哪些?本节课重点探究正多边形的镶嵌 再请同学们仔细观察上下两排镶嵌用的正多边形的种类有何异同?探究活动:
只用一种正多边形,哪几种正多边形能够进行镶嵌?一、用一种正多边形镶嵌平面有空隙有重叠能镶嵌能镶嵌有空隙
不能镶嵌有重叠
不能镶嵌能镶嵌K= 6K= 4K= 3K= 4K= 360°90°108°108°120°n =3n =6n =4n =56×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°
问题:怎样的正多边形能进行平面镶嵌。 规律:如果一种正多边形可以进行镶嵌,
那么内角一定是360°的约数。问题:正八边形能镶嵌平面吗?正九边形呢?135x2<360o
135x3>360o140x2<360o
140x3>360o135o 140o不能镶嵌不能镶嵌问 题:小强搬新家了,他的房间要自己设计,地板想用一种正多边形来镶嵌,那么小强可以有几种选择呢?
一种正多边形进行镶嵌,只有正三角形、正四边形、正六边形三种。3×60°+ 2 ×90°= 360° 2×60°+2 ×120°=360°4×60°+1 ×120°=360°正三角形正四边形正三角形正六边形二、用两种正多边形镶嵌平面你能找出用两种正多边形镶嵌的规律吗?用两种正多边形镶嵌的规律:
(1)拼接在同一个点的各个角的和等于360°
(2)两种正多边形的边长相等.
正三角形与正五边形能进行平面镶嵌吗?为什么?1)正三角形与正方形镶嵌图案设计2)正三角形与正六边形镶嵌图案设计思考1、正四边形与正八边形能进行平面镶嵌吗?为什么?
2、正五边形与正十边形能进行平面镶嵌吗?为什么?
3、正三角形与正十二边形能进行平面镶嵌吗?为什么?
4、正六边形与正八边形能进行平面镶嵌吗?为什么?1×90°+2 ×135°=360°2×108°+1×144°=360°1×60°+2×150°=360°1×60°+2×150°=360°三种:正四边形、正六边形和正十二边形1×90°+ 1×120°+ 1×150°=360°三种:正三边形、正四边形、与正六边形课 堂 小 结 通过本节课的学习,你学到了什么?有什么收获呢?让我们一起回顾与分享吧! 1、平面镶嵌的两个条件:不重叠,无空隙.
2、一种正多边形的镶嵌:
只有三种:正三角形、正四边形、正六边形
规律:正多边形的内角一定是360°的约数
3、两种正多边形的镶嵌:
规律:拼接在同一个点的各个角的和等于360°.1 、关注生活中的数学 2 、关注数学中的美温馨提示小小设计师:1、某足球场需铺设草皮。现有正三角形、
正四边形、正六边形、正八边形、四种形状
的草皮,假如你是一名设计师,你有哪些选
择呢?帮忙设计一下吧! 2、收集平面镶嵌资料,
撰写一篇数学小论文。谢谢光临!
Bye-bye!
不能镶嵌有重叠
不能镶嵌能镶嵌K= 6K= 4K= 3K= 4K= 360°90°108°108°120°n =3n =6n =4n =56×60°= 360°4×90°= 360°4×108°> 360°3×120°= 360°3×108°< 360°
问题:怎样的正多边形能进行平面镶嵌。 规律:如果一种正多边形可以进行镶嵌,
那么内角一定是360°的约数。问题:正八边形能镶嵌平面吗?正九边形呢?135x2<360o
135x3>360o140x2<360o
140x3>360o135o 140o不能镶嵌不能镶嵌问 题:小强搬新家了,他的房间要自己设计,地板想用一种正多边形来镶嵌,那么小强可以有几种选择呢?
一种正多边形进行镶嵌,只有正三角形、正四边形、正六边形三种。3×60°+ 2 ×90°= 360° 2×60°+2 ×120°=360°4×60°+1 ×120°=360°正三角形正四边形正三角形正六边形二、用两种正多边形镶嵌平面你能找出用两种正多边形镶嵌的规律吗?用两种正多边形镶嵌的规律:
(1)拼接在同一个点的各个角的和等于360°
(2)两种正多边形的边长相等.
正三角形与正五边形能进行平面镶嵌吗?为什么?1)正三角形与正方形镶嵌图案设计2)正三角形与正六边形镶嵌图案设计思考1、正四边形与正八边形能进行平面镶嵌吗?为什么?
2、正五边形与正十边形能进行平面镶嵌吗?为什么?
3、正三角形与正十二边形能进行平面镶嵌吗?为什么?
4、正六边形与正八边形能进行平面镶嵌吗?为什么?1×90°+2 ×135°=360°2×108°+1×144°=360°1×60°+2×150°=360°1×60°+2×150°=360°三种:正四边形、正六边形和正十二边形1×90°+ 1×120°+ 1×150°=360°三种:正三边形、正四边形、与正六边形课 堂 小 结 通过本节课的学习,你学到了什么?有什么收获呢?让我们一起回顾与分享吧! 1、平面镶嵌的两个条件:不重叠,无空隙.
2、一种正多边形的镶嵌:
只有三种:正三角形、正四边形、正六边形
规律:正多边形的内角一定是360°的约数
3、两种正多边形的镶嵌:
规律:拼接在同一个点的各个角的和等于360°.1 、关注生活中的数学 2 、关注数学中的美温馨提示小小设计师:1、某足球场需铺设草皮。现有正三角形、
正四边形、正六边形、正八边形、四种形状
的草皮,假如你是一名设计师,你有哪些选
择呢?帮忙设计一下吧! 2、收集平面镶嵌资料,
撰写一篇数学小论文。谢谢光临!
Bye-bye!
