24.1圆的有关性质 强化训练 (含答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1圆的有关性质 强化训练 (含答案)2023-2024学年人教版数学九年级上册 | 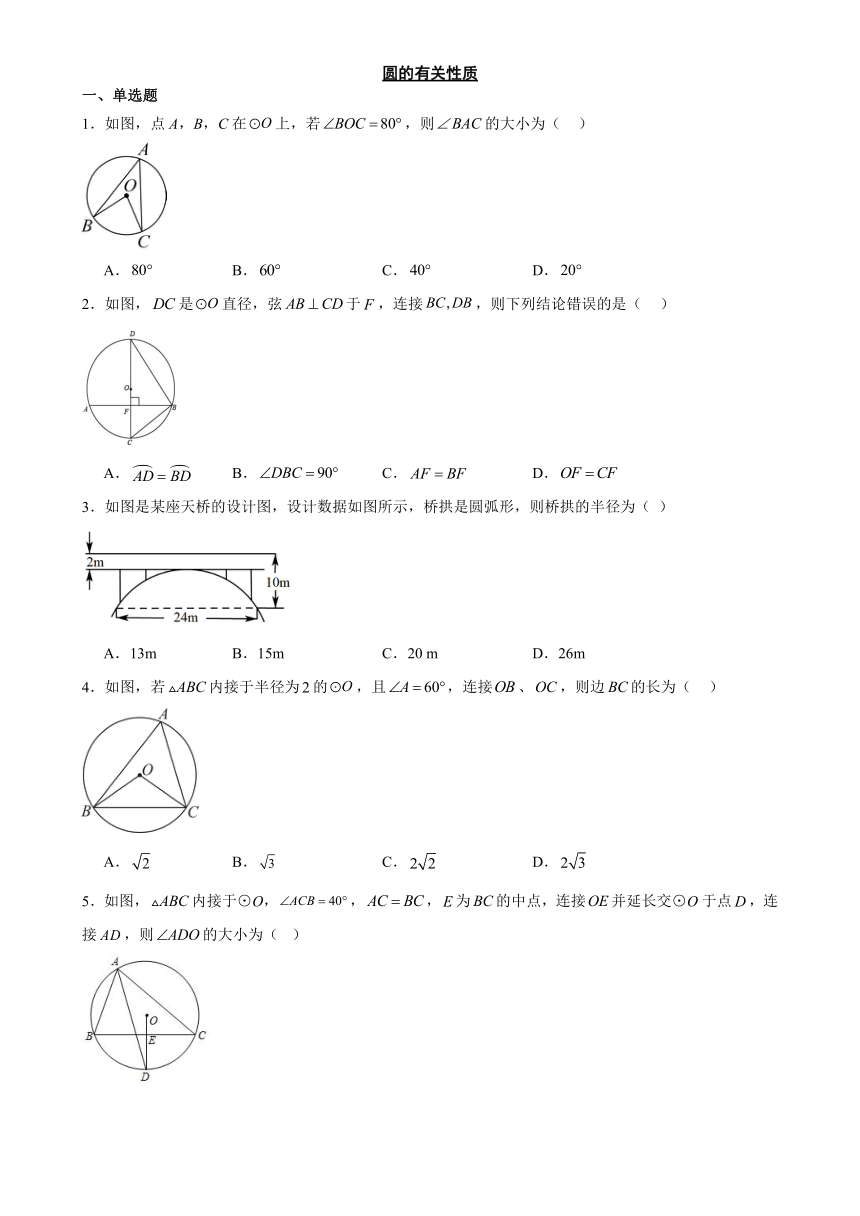 | |
| 格式 | docx | ||
| 文件大小 | 460.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 17:25:15 | ||
图片预览


文档简介
圆的有关性质
一、单选题
1.如图,点A,B,C在上,若,则的大小为( )
A. B. C. D.
2.如图,是直径,弦于,连接,则下列结论错误的是( )
A. B. C. D.
3.如图是某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
A.13m B.15m C.20 m D.26m
4.如图,若内接于半径为的,且,连接、,则边的长为( )
A. B. C. D.
5.如图,内接于⊙O,,,为的中点,连接并延长交⊙O于点,连接,则的大小为( )
A. B. C. D.
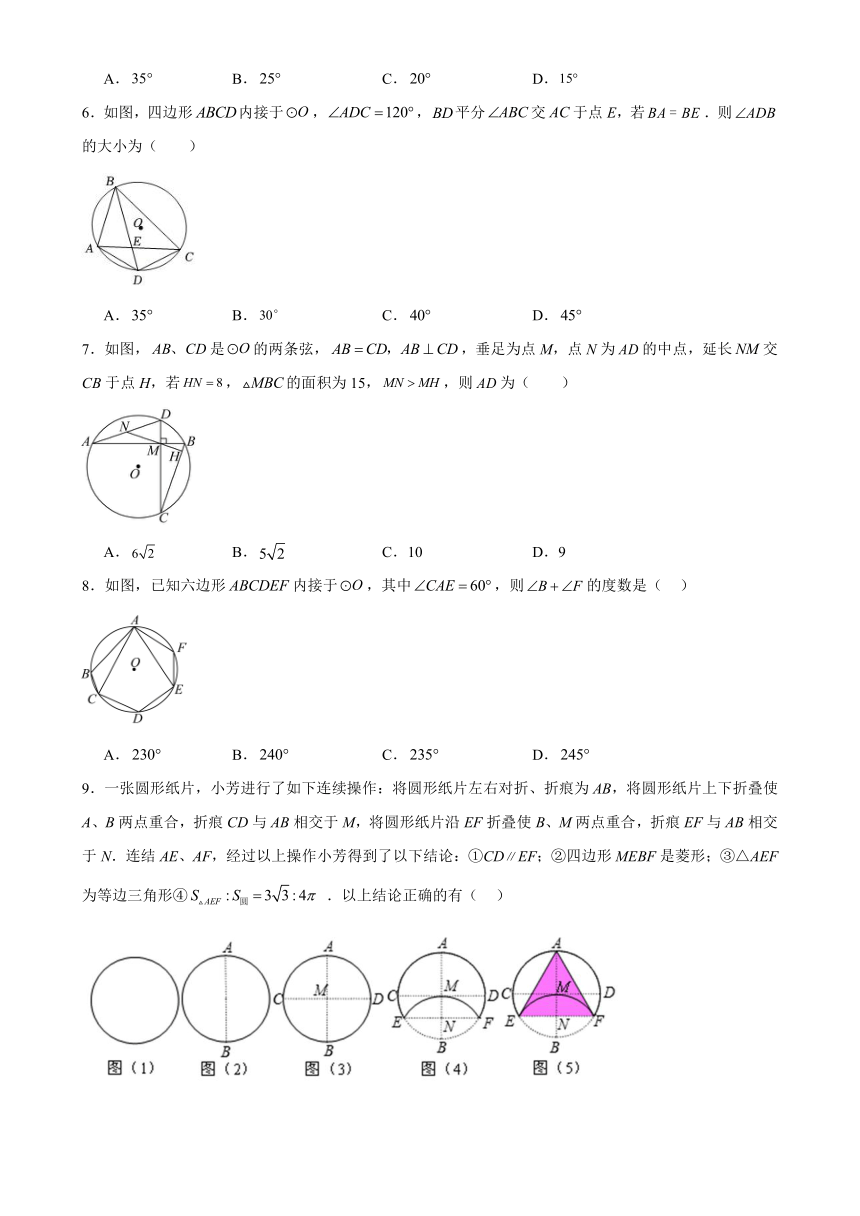
6.如图,四边形内接于,,平分交于点E,若.则的大小为( )
A. B. C. D.
7.如图,是的两条弦,,垂足为点M,点N为的中点,延长交CB于点H,若,的面积为15,,则为( )
A. B. C.10 D.9
8.如图,已知六边形内接于,其中,则的度数是( )
A. B. C. D.
9.一张圆形纸片,小芳进行了如下连续操作:将圆形纸片左右对折、折痕为AB,将圆形纸片上下折叠使A、B两点重合,折痕CD与AB相交于M,将圆形纸片沿EF折叠使B、M两点重合,折痕EF与AB相交于N.连结AE、AF,经过以上操作小芳得到了以下结论:①CDEF;②四边形MEBF是菱形;③△AEF为等边三角形④ .以上结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
10.已知矩形OABC中,O为坐标原点,点A在x轴上,点C在y轴上,B的坐标为(10,5),点P在边BC上,点A关于OP的对称点为A',若点A'到直线BC的距离为4,则点A'的坐标可能为 .
11.如图,,,,是上的四个点,,,则的度数为 .
12.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,为半径的圆,且圆心在水面上方.若圆被水面截得的弦长为,则筒车工作时,盛水桶在水面以下的最大深度为 m.
13.如图,A、B、C、D为⊙O上的点,且 .若∠COD=40°,则∠ADO= 度.
14.如图,AB是⊙O的直径,AB=10cm,M是半圆AB的一个三等分点,N是半圆AB的一个六等分点,P是直径AB上一动点,连接MP、NP,则MP+NP的最小值是 cm.
15.如图,已知半圆O的直径AB=9,C是半圆上一点,沿AC折叠半圆得到,交直径AB于点D,若D在半径OA上,且为直径的三等分点,则AC的长是 .
三、解答题
16.如图,AB、AC为O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,求∠BOC的度数
17.已知的半径为,小明同学作如下操作(如图):
Ⅰ.在上任取一点A,以A为圆心,为半径作弧,与相交于、两点;
Ⅱ.以为圆心,为半径作弧与相交于点;
Ⅲ.分别以、为圆心,、两点间距离为半径作弧相交于点;
Ⅳ.以为圆心,、两点间距离为半径作弧与相交于点;
(1)、两点之间的距离__________;、两点之间的距离__________;
(2)试猜想的度数,并证明你的结论.
18.如图,是的弦,,,垂足分别为M、N,且.
(1)与相等吗?为什么?
(2)判断与是否相等,并说明理由.
19.如图,在上,经过圆心的线段于点,与交于点.
(1)如图1,当半径为,若,求弦的长;
(2)如图2,当半径为 ,,若,求弦的长.
参考答案:
1.C
2.D
3.A
4.D
5.D
6.D
7.C
8.B
9.D
10.(,9)、(,9)或(,1)
11.
12.4
13.30
14.5
15.
16.140°
(1); (2)
18.(1) (2)
19.(1)8 (2)
一、单选题
1.如图,点A,B,C在上,若,则的大小为( )
A. B. C. D.
2.如图,是直径,弦于,连接,则下列结论错误的是( )
A. B. C. D.
3.如图是某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为( )
A.13m B.15m C.20 m D.26m
4.如图,若内接于半径为的,且,连接、,则边的长为( )
A. B. C. D.
5.如图,内接于⊙O,,,为的中点,连接并延长交⊙O于点,连接,则的大小为( )
A. B. C. D.
6.如图,四边形内接于,,平分交于点E,若.则的大小为( )
A. B. C. D.
7.如图,是的两条弦,,垂足为点M,点N为的中点,延长交CB于点H,若,的面积为15,,则为( )
A. B. C.10 D.9
8.如图,已知六边形内接于,其中,则的度数是( )
A. B. C. D.
9.一张圆形纸片,小芳进行了如下连续操作:将圆形纸片左右对折、折痕为AB,将圆形纸片上下折叠使A、B两点重合,折痕CD与AB相交于M,将圆形纸片沿EF折叠使B、M两点重合,折痕EF与AB相交于N.连结AE、AF,经过以上操作小芳得到了以下结论:①CDEF;②四边形MEBF是菱形;③△AEF为等边三角形④ .以上结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
10.已知矩形OABC中,O为坐标原点,点A在x轴上,点C在y轴上,B的坐标为(10,5),点P在边BC上,点A关于OP的对称点为A',若点A'到直线BC的距离为4,则点A'的坐标可能为 .
11.如图,,,,是上的四个点,,,则的度数为 .
12.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,如图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,为半径的圆,且圆心在水面上方.若圆被水面截得的弦长为,则筒车工作时,盛水桶在水面以下的最大深度为 m.
13.如图,A、B、C、D为⊙O上的点,且 .若∠COD=40°,则∠ADO= 度.
14.如图,AB是⊙O的直径,AB=10cm,M是半圆AB的一个三等分点,N是半圆AB的一个六等分点,P是直径AB上一动点,连接MP、NP,则MP+NP的最小值是 cm.
15.如图,已知半圆O的直径AB=9,C是半圆上一点,沿AC折叠半圆得到,交直径AB于点D,若D在半径OA上,且为直径的三等分点,则AC的长是 .
三、解答题
16.如图,AB、AC为O的两条弦,延长CA到D,使AD=AB,如果∠ADB=35°,求∠BOC的度数
17.已知的半径为,小明同学作如下操作(如图):
Ⅰ.在上任取一点A,以A为圆心,为半径作弧,与相交于、两点;
Ⅱ.以为圆心,为半径作弧与相交于点;
Ⅲ.分别以、为圆心,、两点间距离为半径作弧相交于点;
Ⅳ.以为圆心,、两点间距离为半径作弧与相交于点;
(1)、两点之间的距离__________;、两点之间的距离__________;
(2)试猜想的度数,并证明你的结论.
18.如图,是的弦,,,垂足分别为M、N,且.
(1)与相等吗?为什么?
(2)判断与是否相等,并说明理由.
19.如图,在上,经过圆心的线段于点,与交于点.
(1)如图1,当半径为,若,求弦的长;
(2)如图2,当半径为 ,,若,求弦的长.
参考答案:
1.C
2.D
3.A
4.D
5.D
6.D
7.C
8.B
9.D
10.(,9)、(,9)或(,1)
11.
12.4
13.30
14.5
15.
16.140°
(1); (2)
18.(1) (2)
19.(1)8 (2)
同课章节目录
