八年级数学上册试题 期中测试卷-苏科版(含答案)
文档属性
| 名称 | 八年级数学上册试题 期中测试卷-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 155.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 17:26:05 | ||
图片预览




文档简介
期中测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
2.到三角形的三个顶点距离相等的点是( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
3.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.①和③ C.②和④ D.③和④
4.已知等腰三角形的周长为29,其中一边长为7,则该等腰三角形的底边长为( )
A.11 B.7 C.15 D.15或7
5.下列各组数据中,不能作为直角三角形三边长的是( )
A.9,12,15 B.3,4,5 C.1,2,3 D.40,41,9
6.如图,已知AB=AC,添加下列条件仍不能使△ABD≌△ACD的是( )
A.∠B=∠C=90° B.AD平分∠BAC C.AD平分∠BDC D.BD=CD
7.如图,在△ABC中,∠ACB=90°,∠B=30°,AD平分∠BAC,E是AD中点,若BD=9,则CE的长为( )
A.3 B.3.5 C.4 D.4.5
8.如图,∠AOB=60°,点P在边OA上,OP=22,点M、N在边OB上(M在N的左侧),且PM=PN,若MN=4,则OM的长为( )
A.7 B.8 C.9 D.11
9.如图,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
A. B. C. D.
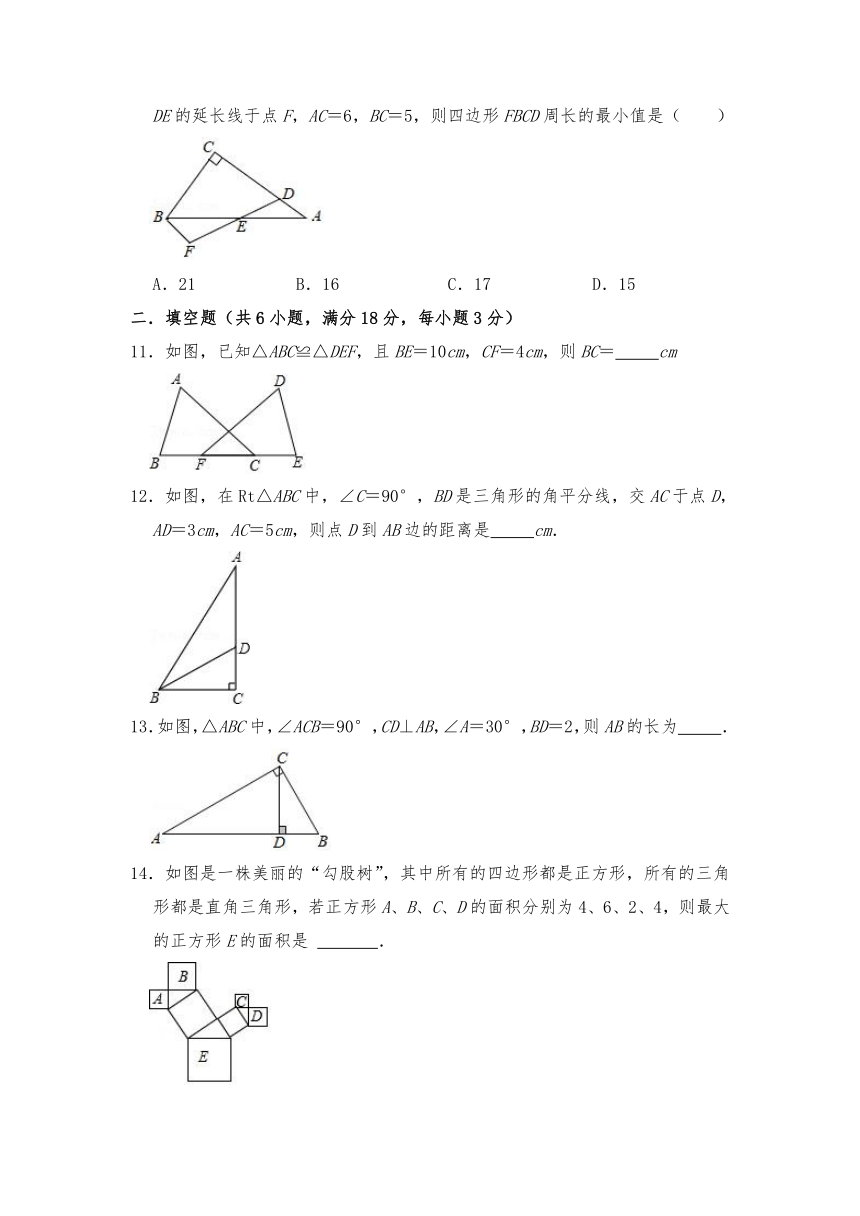
10.如图,Rt△ABC中,∠C=90°,E为AB中点,D为AC上一点,BF∥AC交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是( )
A.21 B.16 C.17 D.15
二.填空题(共6小题,满分18分,每小题3分)
11.如图,已知△ABC≌△DEF,且BE=10cm,CF=4cm,则BC= cm
12.如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=3cm,AC=5cm,则点D到AB边的距离是 cm.
13.如图,△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,BD=2,则AB的长为 .
14.如图是一株美丽的“勾股树”,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为4、6、2、4,则最大的正方形E的面积是 .
15.如图,在△ABC中,∠BCA>90°,∠ACB=2∠B,CD是∠ACB的平分线,CE⊥AB于点E,过点A作CD的垂线交CD的延长线于点H,若CH=5,CE=3,则△ABC的面积为 .
16.已知Rt△ABC的两直角边不相等,如果要画一个三角形与Rt△ABC全等,且使所画三角形两条直角边与Rt△ABC的两条直角边分别在同一条直线上(Rt△ABC本身不算),那么满足上述条件的三角形最多能画出 个.
三.解答题(共7小题,满分52分)
17.(6分)已知直线l及其两侧两点A、B,如图.
(1)在直线l上求一点P,使PA=PB;
(2)在直线l上求一点Q,使l平分∠AQB.
(以上两小题保留作图痕迹,标出必要的字母,不要求写作法)
18.(6分)如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
19.(8分)在一次“探究性学习”课中,数学老师给出如下表所示的数据:
(1)请你认真观察线段a、b、c的长与n之间的关系,用含n(n为自然数,且n>1)的代数式表示:
a= ; b= ; c= .
(2)猜想:以线段a、b、c为边的三角形是否是直角三角形?并说明你的结论.
20.(8分)如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.
21.(8分)如图,在△ABC中,AB=AC,点D为AC上一点,且满足AD=BD=BC.点E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.
(1)求∠BAC和∠ACB的度数;
(2)求证:△ACF是等腰三角形.
22.(8分)如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.试说明:
(1)△ABP≌△AEQ;
(2)EF=BF.
23.(8分)如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
答案
一.选择题
B.D.B.B.C.C.D.C.B.B.
二.填空题
11.7.
12.2.
13.8.
14.16.
15.15.
16.7.
三.解答题
17.解:
18.解:设AE=xkm,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∵C、D两村到E站的距离相等,
∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25﹣x)2,
解得,x=10.
故:E点应建在距A站10千米处.
19.解:(1)根据表格中的数据可得:a=n2﹣1,b=2n,c=n2+1;
(2)∵(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2,
∴能够成直角三角形.
20.解:∵DE为AB的垂直平分线,
∴∠A=∠ABD,
又∵∠ABD=2∠CBD,
∴∠A=∠ABD=2∠CBD,
设∠A=α,则∠ABD=α,∠CBDα,
又∵∠C=90°,
∴∠A+∠ABC=90°,
即α+αα=90°,
解得α=36°,
∴∠A=36°.
21.解:(1)设∠BAC=x°,
∵AD=BD,
∴∠A=∠ABD=x°,
∴∠BDC=2x°,
∵BD=BC,
∴∠BDC=∠BCD=2x°,
∵AB=AC,
∴∠ABC=∠ACB=2x°,
由∠BAC+∠ABC+∠ACB=180°可得x+2x+2x=180,
解得:x=36,
则∠BAC=36°,∠ACB=72°;
(2)∵E是AB的中点,AD=BD,
∴DE⊥AB,即FE⊥AB;
∴AF=BF,
∴∠BAF=∠ABF,
又∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°,
又∵∠ACB=72°,
∴∠AFC=∠ACB﹣∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形.
22.解:(1)∵△ABE和△APQ是等边三角形,
∴AB=AE,AP=AQ,∠BAE=∠PAQ=∠ABE=∠AEB=60°,
∴∠BAE﹣∠PAE=∠PAQ﹣∠PAE,
∴∠BAP=∠EAQ.
在△ABP和△AEQ中,
,
∴△QAE≌△PAB(SAS);
(2)∵△QAE≌△PAB
∴∠ABP=∠AEQ=90°.
∴∠AEF=90°,
∴∠ABP=∠AEF
∴∠ABP﹣∠AEB=∠AEF﹣∠ABE,
∴∠BEF=∠EBF,
∴BF=EF.
23.解:(1)当t=1时,AP=BQ=1,BP=AC=3,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
,
解得
;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得
;
综上所述,存在
或
使得△ACP与△BPQ全等.
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图案中,不是轴对称图案的是( )
A. B.
C. D.
2.到三角形的三个顶点距离相等的点是( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
3.下列四个图形中,有两个全等的图形,它们是( )
A.①和② B.①和③ C.②和④ D.③和④
4.已知等腰三角形的周长为29,其中一边长为7,则该等腰三角形的底边长为( )
A.11 B.7 C.15 D.15或7
5.下列各组数据中,不能作为直角三角形三边长的是( )
A.9,12,15 B.3,4,5 C.1,2,3 D.40,41,9
6.如图,已知AB=AC,添加下列条件仍不能使△ABD≌△ACD的是( )
A.∠B=∠C=90° B.AD平分∠BAC C.AD平分∠BDC D.BD=CD
7.如图,在△ABC中,∠ACB=90°,∠B=30°,AD平分∠BAC,E是AD中点,若BD=9,则CE的长为( )
A.3 B.3.5 C.4 D.4.5
8.如图,∠AOB=60°,点P在边OA上,OP=22,点M、N在边OB上(M在N的左侧),且PM=PN,若MN=4,则OM的长为( )
A.7 B.8 C.9 D.11
9.如图,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
A. B. C. D.
10.如图,Rt△ABC中,∠C=90°,E为AB中点,D为AC上一点,BF∥AC交DE的延长线于点F,AC=6,BC=5,则四边形FBCD周长的最小值是( )
A.21 B.16 C.17 D.15
二.填空题(共6小题,满分18分,每小题3分)
11.如图,已知△ABC≌△DEF,且BE=10cm,CF=4cm,则BC= cm
12.如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=3cm,AC=5cm,则点D到AB边的距离是 cm.
13.如图,△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,BD=2,则AB的长为 .
14.如图是一株美丽的“勾股树”,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为4、6、2、4,则最大的正方形E的面积是 .
15.如图,在△ABC中,∠BCA>90°,∠ACB=2∠B,CD是∠ACB的平分线,CE⊥AB于点E,过点A作CD的垂线交CD的延长线于点H,若CH=5,CE=3,则△ABC的面积为 .
16.已知Rt△ABC的两直角边不相等,如果要画一个三角形与Rt△ABC全等,且使所画三角形两条直角边与Rt△ABC的两条直角边分别在同一条直线上(Rt△ABC本身不算),那么满足上述条件的三角形最多能画出 个.
三.解答题(共7小题,满分52分)
17.(6分)已知直线l及其两侧两点A、B,如图.
(1)在直线l上求一点P,使PA=PB;
(2)在直线l上求一点Q,使l平分∠AQB.
(以上两小题保留作图痕迹,标出必要的字母,不要求写作法)
18.(6分)如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
19.(8分)在一次“探究性学习”课中,数学老师给出如下表所示的数据:
(1)请你认真观察线段a、b、c的长与n之间的关系,用含n(n为自然数,且n>1)的代数式表示:
a= ; b= ; c= .
(2)猜想:以线段a、b、c为边的三角形是否是直角三角形?并说明你的结论.
20.(8分)如图,在△ABC中,∠C=90°,DE为AB的垂直平分线,DE交AC于点D,连接BD.若∠ABD=2∠CBD,求∠A的度数.
21.(8分)如图,在△ABC中,AB=AC,点D为AC上一点,且满足AD=BD=BC.点E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.
(1)求∠BAC和∠ACB的度数;
(2)求证:△ACF是等腰三角形.
22.(8分)如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.试说明:
(1)△ABP≌△AEQ;
(2)EF=BF.
23.(8分)如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
答案
一.选择题
B.D.B.B.C.C.D.C.B.B.
二.填空题
11.7.
12.2.
13.8.
14.16.
15.15.
16.7.
三.解答题
17.解:
18.解:设AE=xkm,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∵C、D两村到E站的距离相等,
∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25﹣x)2,
解得,x=10.
故:E点应建在距A站10千米处.
19.解:(1)根据表格中的数据可得:a=n2﹣1,b=2n,c=n2+1;
(2)∵(n2﹣1)2+(2n)2=n4﹣2n2+1+4n2=n4+2n2+1=(n2+1)2,
∴能够成直角三角形.
20.解:∵DE为AB的垂直平分线,
∴∠A=∠ABD,
又∵∠ABD=2∠CBD,
∴∠A=∠ABD=2∠CBD,
设∠A=α,则∠ABD=α,∠CBDα,
又∵∠C=90°,
∴∠A+∠ABC=90°,
即α+αα=90°,
解得α=36°,
∴∠A=36°.
21.解:(1)设∠BAC=x°,
∵AD=BD,
∴∠A=∠ABD=x°,
∴∠BDC=2x°,
∵BD=BC,
∴∠BDC=∠BCD=2x°,
∵AB=AC,
∴∠ABC=∠ACB=2x°,
由∠BAC+∠ABC+∠ACB=180°可得x+2x+2x=180,
解得:x=36,
则∠BAC=36°,∠ACB=72°;
(2)∵E是AB的中点,AD=BD,
∴DE⊥AB,即FE⊥AB;
∴AF=BF,
∴∠BAF=∠ABF,
又∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°,
又∵∠ACB=72°,
∴∠AFC=∠ACB﹣∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形.
22.解:(1)∵△ABE和△APQ是等边三角形,
∴AB=AE,AP=AQ,∠BAE=∠PAQ=∠ABE=∠AEB=60°,
∴∠BAE﹣∠PAE=∠PAQ﹣∠PAE,
∴∠BAP=∠EAQ.
在△ABP和△AEQ中,
,
∴△QAE≌△PAB(SAS);
(2)∵△QAE≌△PAB
∴∠ABP=∠AEQ=90°.
∴∠AEF=90°,
∴∠ABP=∠AEF
∴∠ABP﹣∠AEB=∠AEF﹣∠ABE,
∴∠BEF=∠EBF,
∴BF=EF.
23.解:(1)当t=1时,AP=BQ=1,BP=AC=3,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
∴△ACP≌△BPQ(SAS).
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直.
(2)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
,
解得
;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
,
解得
;
综上所述,存在
或
使得△ACP与△BPQ全等.
同课章节目录
