勾股定理的逆定理课件
图片预览






文档简介
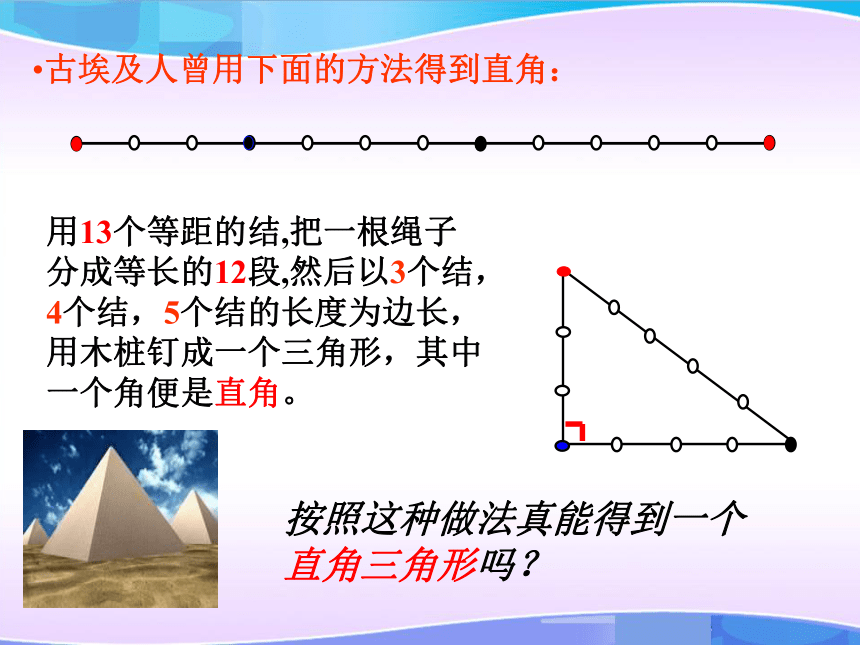
课件39张PPT。18.2 勾股定理的逆定理古埃及人曾用下面的方法得到直角预习交流按照这种做法真能得到一个直角三角形吗? 古埃及人曾用下面的方法得到直角:用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
做一做用圆规、直尺作△ABC,使AB=5cm,AC=4cm,BC=3cm,如图,量一量∠C,它是90°吗?∠C是直角吗?为什么用上面的三条线段围成的三角形,就一定是直角三角形呢?它们的三边有怎样的关系?学习目标
1.理解勾股定理的逆定理,经历“观察-测量-猜想-论证”的定理探究的过程,体会“构造法”证明数学命题的基本思想;
2.了解逆命题的概念,知道原命题为真命题,它的逆命题不一定为真命题.
合作探究 如果三角形的三边分别是5cm,12cm,13cm,有下列的关系: .
那么画出的三角形是直角三角形吗?
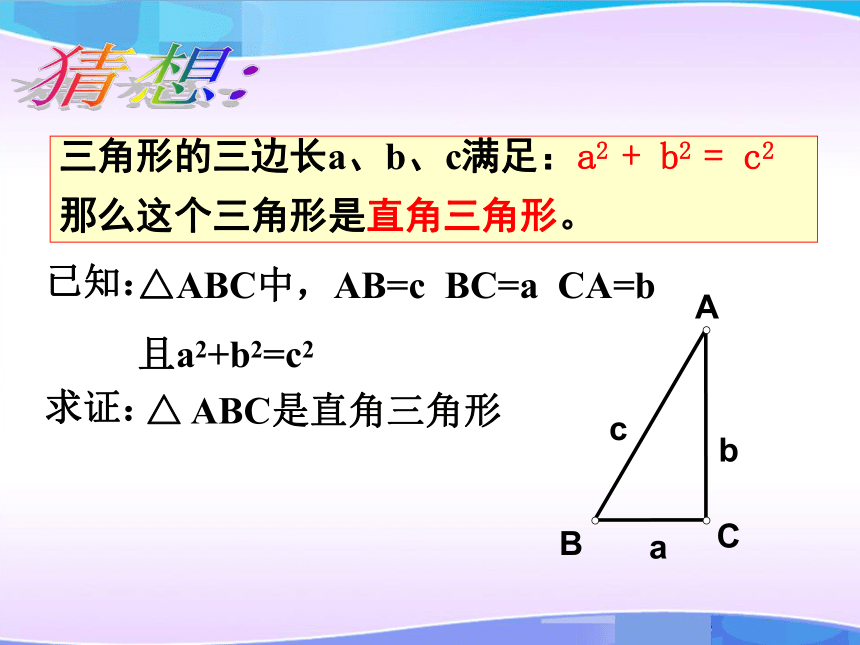
换成三边分别是6cm,8cm,10cm呢?猜想:三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。已知:△ABC中,AB=c BC=a CA=b
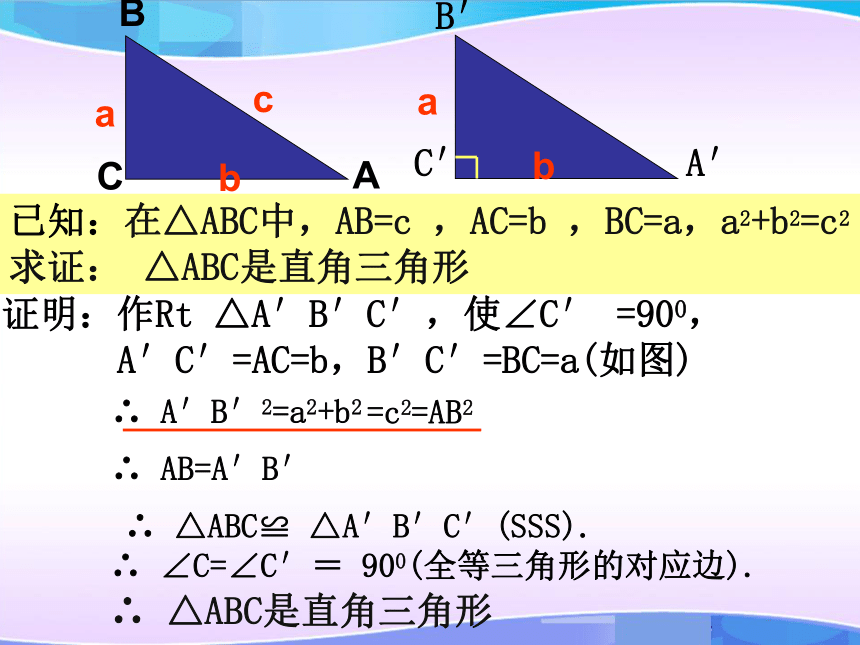
且a2+b2=c2求证:△ ABC是直角三角形证明:作Rt △A′B′C′,使∠C′ =900,
A′C′=AC=b,B′C′=BC=a(如图)∴ A′B′2=a2+b2∴ AB=A′B′
∴ △ABC≌ △A′B′C′(SSS).∴ ∠C=∠C′= 900(全等三角形的对应边).abcab已知:在△ABC中,AB=c ,AC=b ,BC=a,a2+b2=c2
求证: △ABC是直角三角形=c2=AB2∴ △ABC是直角三角形 2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。abc
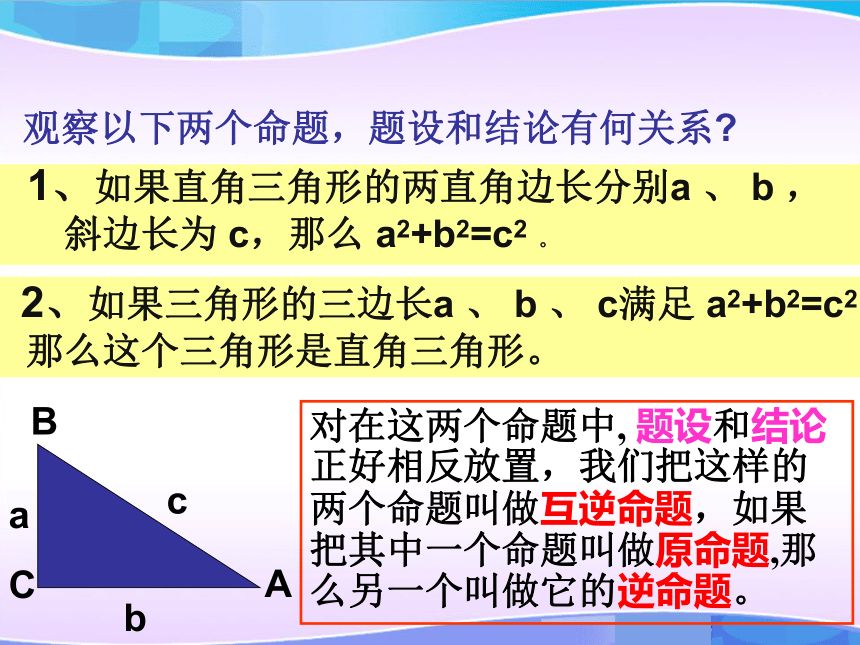
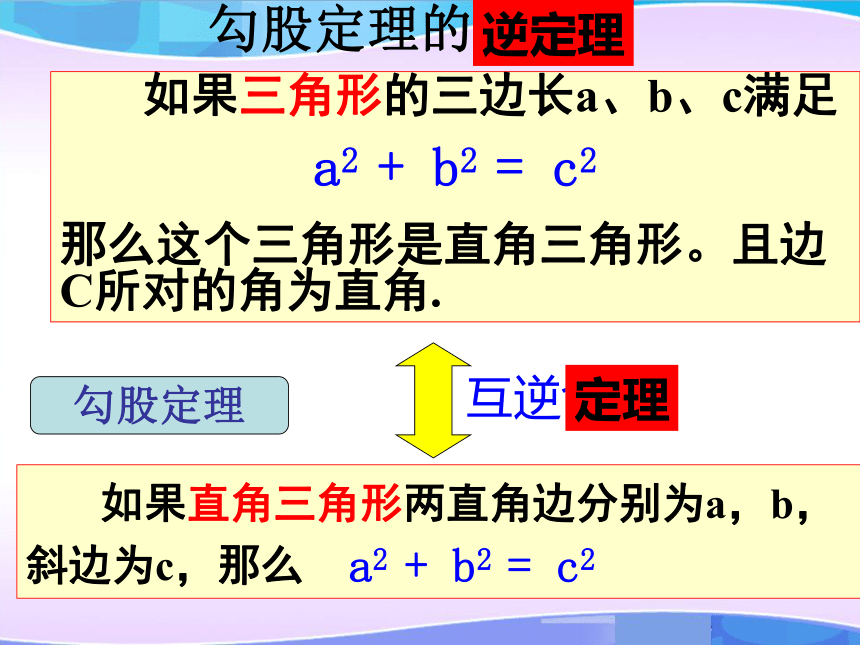
1、如果直角三角形的两直角边长分别a 、 b , 斜边长为 c,那么 a2+b2=c2 。观察以下两个命题,题设和结论有何关系?
对在这两个命题中, 题设和结论正好相反放置,我们把这样的两个命题叫做互逆命题,如果把其中一个命题叫做原命题,那么另一个叫做它的逆命题。
勾股定理的逆命题勾股定理互逆命题逆定理定理 如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。勾股定理的逆定理(1)上述结论中,哪条边所对的角是直角?
(2)如果三角形中较短两边的平方和不等于
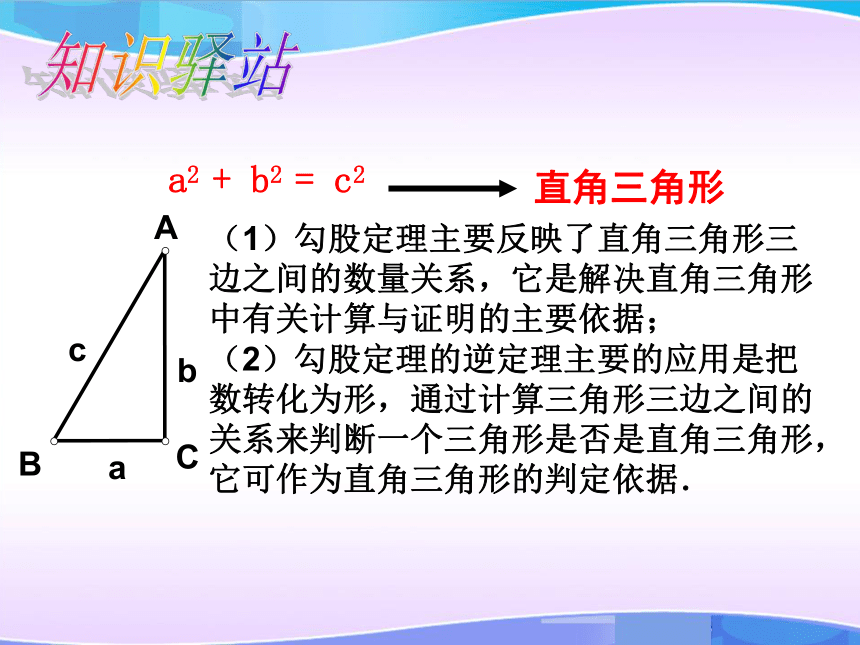
最长的平方,那么这个三角形是直角三角形吗?想一想:知识驿站 (1)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(2)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据.例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方.解:∵152+82=225+64=289,
172=289,
∴ 152+82=172.
∴这个三角形是直角三角形. 像15,8,17,能够成为直角三角形三条边长的三个正整数,称为勾股数.解:∵132+142=169+196=365,
152=225,
∴ 132+142≠152.
∴根据勾股定理,这个三角形是直角三角形.1、判断下列△ABC是不是直角三角形?(3) a=15 b=20 c=25 (1) a=1 b=2 c= (2) a=13 b=14 c=15 (4) a:b: c=3:4:5 练 习 2、观察下列表格:能够成为直角三角形三条边长的
三个正整数,称为勾股数挑战自我84853、古希腊的哲学家柏拉图曾指出:如果m
表示大于1的整数,a=2m,b=m2-1,c=m2+1,
那么a、b、c为勾股数,你认为对吗?(一)选择题: 达标检测 1.在已知下列三组长度的线段中,不能构
成直角三角形的是 ( )
(A)5、12、13 (B)2、3、
(C)4、7、5 (D)1、 、 C (一)选择题: 2.下列命题中,假命题是 ( )
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : : 2的三角形是直角三角形
(C)三边长度之比为1 : : 2的三角形是直角三角形
(D)三边长度之比为 : : 2的三角形是直角三角形 B 3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 这个三角形是直角三角形. (二)解答题: 1.已知:a=m2-n2,b=2mn,c=m2+n2
(m、n为正整数,m>n).
试判定由a、b、c组成的三角形是不是直
角三角形. 思考1:△ABC三边a,b,c为边向外作正方形,若S1+S2=S3成立,则△ABC是什么三角形?为什么?思考2:已知△ABC是直角三角形,以
a,b,c为边向外作正方形,有S1+S2=S3?
为什么?思考交流a2 + b2 = c2直角三角形直角三角形a2 + b2 = c2 例1 某港口P位于东西方向的海岸线上.“远航”
号、“海天”号轮船同时离开港口,各自沿一固定方向
航行,“远航”号每小时航行16 n mile,“海天”号每
小时航行12 n mile.它们离开港口一个半小时后分别位
于点Q,R处,且相距
30 n mile .如果知道
“远航”号沿东北方
向航行,能知道“海
天”号沿哪个方向航
行吗?拓广与应用 例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为解:∵152+82=172
∴a2+c2=b2
1.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
2.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。变式训练勾股定理与逆定理的综合运用3.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
下面来看定理的应用.
例1 根据下列三角形的三边a、b、c的值,判断三角形是不是直角三角形。如果是,指出哪条边所对的角是直角?
(1)a=7,b=24,c=25;
(2)a=7,b=8,c=11.解(1)∵最大边是c=25,c2=625,
a2+b2=72+242=625,
∴a2+b2=c2,
∴△ABC是直角三角形,
最大边c所对的角是直角.
第(2)题由同学们仿照上面自己解答.练习一下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ________ ________(3) a=13 b=14 c=15 _______ ________(4) a:b: c=3:4:5 ________ ________是∠ A=900(2) a=1 b=2 c= ________ ________∠ B=900是不是∠ C=900是例2 已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).求证:△ABC为直角三角形.
分析: 在a、b、c三边中,哪一条边是最大的边?需要得出什么,才能证明△ABC为直角三角形?
请同学们自己完成证明过程.
能够成为直角三角形三条边长度的三个正整数,称为勾股数.
思考:除3、4、5外,再写出3组勾股数.想想看,可以怎样找?1.判断下列三个边长组成的三角形是不是直角三角形? (1)a=2,b=3,c=4. (2)a=9,b=7,c=12. (3)a=25,b=20,c=15. 2.在△ABC中,三边长a、b、c满足(a+c)(a-c)=b2,则△ABC是什么三角形? 3.给你一根带有刻度的皮尺,你如何用它来判断课桌面的角是直角?用这种办法能判断柱子是否与地面垂直吗?练习二 再观察下面两组命题:请说出上面两个命题的逆命题。如果两个角是对顶角,那么它们相等。
三角形中相等的边所对的角相等。
它们都正确吗?想一想:一个命题是真命题,它的逆命题是真命 题还是假命题?如果两个角是对顶角,那么它们相等。
如果两个角相等,那么它们是对顶角。三角形中相等的边所对的角相等。
三角形中相等的角所对的边相等。一个命题的逆命题可能是真命题也可能是假命题。正确不正确正确正确 2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。abc
1、如果直角三角形的两直角边长分别a 、b,斜边长为 c,那么 a2+b2=c2 。勾股定理
勾股定理的逆定理
一般地,如果一个定理的逆命题
经过证明是正确的,它也是一个
定理,则称两个定理互为逆定理。
这是判定直角三角形的根据之一、、1什么叫命题?命题由几部分组成?
命题的种类有几种?命题的一般形式如何?命题:“两直线平行,内错角相等.”题设是: ,
结论是: .内错角相等两直线平行内错角相等,两直线平行.这个命题的逆命题:互逆命题的题设和结论反过来.(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的绝对值相等.
(3)全等三角形的对应角相等
(4)角的内部到角的两边距离相等的点在角的平分线上. .说出下列命题的逆命题.并这些命题的真假性.逆命题: 内错角相等,两条直线平行. 逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 逆命题:三个角对应相等的两个三角形是全等三角形. 逆命题:角平分线上的点到角两边的距离相等.感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.真命题假命题假命题真命题1、下列各组线段中,能够围成直角三角形的是 ( )
A、1、2、3 B、15、20、25
C、4、5、6 D、18、9、102、下列各组线段中,不能够围成直角三角形是 ( )
A、9、12、15 B、8、15、17
C、7、24、25 D、6、8、9BDCA、锐角三角形 B、钝角三角形
C、直角三角形 D、等边三角形4.解:(3)∵12+( )2=1+3=4,
22=4,
∴ 12+( )2=22.
∴这个三角形是直角三角形.(3)a=1,b=2,c= ; (4)a:b:c=3:4:5. 6.判断由a、b、c组成的三角形是不是直角三角形:(4)设a=3x, b=4x, c=5x,则
∵(3x)2+(4x )2=25x2,
(5x)2= 25x2,
∴ (3x)2+(4x )2 = (5x)2.
∴这个三角形是直角三角形.2.说出下列命题的逆命题.这些命题的逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相 等;
(3)全等三角形的对应角相等;
(4)到角的两边距离相等的点在角的平分线上.练习
做一做用圆规、直尺作△ABC,使AB=5cm,AC=4cm,BC=3cm,如图,量一量∠C,它是90°吗?∠C是直角吗?为什么用上面的三条线段围成的三角形,就一定是直角三角形呢?它们的三边有怎样的关系?学习目标
1.理解勾股定理的逆定理,经历“观察-测量-猜想-论证”的定理探究的过程,体会“构造法”证明数学命题的基本思想;
2.了解逆命题的概念,知道原命题为真命题,它的逆命题不一定为真命题.
合作探究 如果三角形的三边分别是5cm,12cm,13cm,有下列的关系: .
那么画出的三角形是直角三角形吗?
换成三边分别是6cm,8cm,10cm呢?猜想:三角形的三边长a、b、c满足:a2 + b2 = c2
那么这个三角形是直角三角形。已知:△ABC中,AB=c BC=a CA=b
且a2+b2=c2求证:△ ABC是直角三角形证明:作Rt △A′B′C′,使∠C′ =900,
A′C′=AC=b,B′C′=BC=a(如图)∴ A′B′2=a2+b2∴ AB=A′B′
∴ △ABC≌ △A′B′C′(SSS).∴ ∠C=∠C′= 900(全等三角形的对应边).abcab已知:在△ABC中,AB=c ,AC=b ,BC=a,a2+b2=c2
求证: △ABC是直角三角形=c2=AB2∴ △ABC是直角三角形 2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。abc
1、如果直角三角形的两直角边长分别a 、 b , 斜边长为 c,那么 a2+b2=c2 。观察以下两个命题,题设和结论有何关系?
对在这两个命题中, 题设和结论正好相反放置,我们把这样的两个命题叫做互逆命题,如果把其中一个命题叫做原命题,那么另一个叫做它的逆命题。
勾股定理的逆命题勾股定理互逆命题逆定理定理 如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。勾股定理的逆定理(1)上述结论中,哪条边所对的角是直角?
(2)如果三角形中较短两边的平方和不等于
最长的平方,那么这个三角形是直角三角形吗?想一想:知识驿站 (1)勾股定理主要反映了直角三角形三边之间的数量关系,它是解决直角三角形中有关计算与证明的主要依据;
(2)勾股定理的逆定理主要的应用是把数转化为形,通过计算三角形三边之间的关系来判断一个三角形是否是直角三角形,它可作为直角三角形的判定依据.例1 判断由a、b、c组成的三角形是不是直角三角形:
(1) a=15 , b =8 , c=17(2) a=13 , b =15 , c=14分析:由勾股定理的逆定理,判断三角形是不是直角三角形,只要看两条较小边的平方和是否等于最大边的平方.解:∵152+82=225+64=289,
172=289,
∴ 152+82=172.
∴这个三角形是直角三角形. 像15,8,17,能够成为直角三角形三条边长的三个正整数,称为勾股数.解:∵132+142=169+196=365,
152=225,
∴ 132+142≠152.
∴根据勾股定理,这个三角形是直角三角形.1、判断下列△ABC是不是直角三角形?(3) a=15 b=20 c=25 (1) a=1 b=2 c= (2) a=13 b=14 c=15 (4) a:b: c=3:4:5 练 习 2、观察下列表格:能够成为直角三角形三条边长的
三个正整数,称为勾股数挑战自我84853、古希腊的哲学家柏拉图曾指出:如果m
表示大于1的整数,a=2m,b=m2-1,c=m2+1,
那么a、b、c为勾股数,你认为对吗?(一)选择题: 达标检测 1.在已知下列三组长度的线段中,不能构
成直角三角形的是 ( )
(A)5、12、13 (B)2、3、
(C)4、7、5 (D)1、 、 C (一)选择题: 2.下列命题中,假命题是 ( )
(A)三个角的度数之比为1 : 3 : 4的三角形是直角三角形
(B)三个角的度数之比为1 : : 2的三角形是直角三角形
(C)三边长度之比为1 : : 2的三角形是直角三角形
(D)三边长度之比为 : : 2的三角形是直角三角形 B 3.如果△ABC的三边分别为a、b、c且满足
a2+b2+c2+50=6a+8b+10c,
判定△ABC的形状. (二)解答题: 这个三角形是直角三角形. (二)解答题: 1.已知:a=m2-n2,b=2mn,c=m2+n2
(m、n为正整数,m>n).
试判定由a、b、c组成的三角形是不是直
角三角形. 思考1:△ABC三边a,b,c为边向外作正方形,若S1+S2=S3成立,则△ABC是什么三角形?为什么?思考2:已知△ABC是直角三角形,以
a,b,c为边向外作正方形,有S1+S2=S3?
为什么?思考交流a2 + b2 = c2直角三角形直角三角形a2 + b2 = c2 例1 某港口P位于东西方向的海岸线上.“远航”
号、“海天”号轮船同时离开港口,各自沿一固定方向
航行,“远航”号每小时航行16 n mile,“海天”号每
小时航行12 n mile.它们离开港口一个半小时后分别位
于点Q,R处,且相距
30 n mile .如果知道
“远航”号沿东北方
向航行,能知道“海
天”号沿哪个方向航
行吗?拓广与应用 例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为解:∵152+82=172
∴a2+c2=b2
1.如图:AD⊥CD , AC⊥BC ,AB=13, CD=3 , AD=4 。求:(1)求AC长
(2)求BC长
2.如图, AD⊥CD ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)∠ACB的度数。变式训练勾股定理与逆定理的综合运用3.如图, AC⊥BC ,AB=13, BC=12 ,CD=3 , AD=4 。求:(1)求AC长
(2)求 的面积。
下面来看定理的应用.
例1 根据下列三角形的三边a、b、c的值,判断三角形是不是直角三角形。如果是,指出哪条边所对的角是直角?
(1)a=7,b=24,c=25;
(2)a=7,b=8,c=11.解(1)∵最大边是c=25,c2=625,
a2+b2=72+242=625,
∴a2+b2=c2,
∴△ABC是直角三角形,
最大边c所对的角是直角.
第(2)题由同学们仿照上面自己解答.练习一下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 ________ ________(3) a=13 b=14 c=15 _______ ________(4) a:b: c=3:4:5 ________ ________是∠ A=900(2) a=1 b=2 c= ________ ________∠ B=900是不是∠ C=900是例2 已知:在△ABC中,三条边长分别为a=n2-1,b=2n,c=n2+1(n>1).求证:△ABC为直角三角形.
分析: 在a、b、c三边中,哪一条边是最大的边?需要得出什么,才能证明△ABC为直角三角形?
请同学们自己完成证明过程.
能够成为直角三角形三条边长度的三个正整数,称为勾股数.
思考:除3、4、5外,再写出3组勾股数.想想看,可以怎样找?1.判断下列三个边长组成的三角形是不是直角三角形? (1)a=2,b=3,c=4. (2)a=9,b=7,c=12. (3)a=25,b=20,c=15. 2.在△ABC中,三边长a、b、c满足(a+c)(a-c)=b2,则△ABC是什么三角形? 3.给你一根带有刻度的皮尺,你如何用它来判断课桌面的角是直角?用这种办法能判断柱子是否与地面垂直吗?练习二 再观察下面两组命题:请说出上面两个命题的逆命题。如果两个角是对顶角,那么它们相等。
三角形中相等的边所对的角相等。
它们都正确吗?想一想:一个命题是真命题,它的逆命题是真命 题还是假命题?如果两个角是对顶角,那么它们相等。
如果两个角相等,那么它们是对顶角。三角形中相等的边所对的角相等。
三角形中相等的角所对的边相等。一个命题的逆命题可能是真命题也可能是假命题。正确不正确正确正确 2、如果三角形的三边长a 、 b 、 c满足 a2+b2=c2 ,
那么这个三角形是直角三角形。abc
1、如果直角三角形的两直角边长分别a 、b,斜边长为 c,那么 a2+b2=c2 。勾股定理
勾股定理的逆定理
一般地,如果一个定理的逆命题
经过证明是正确的,它也是一个
定理,则称两个定理互为逆定理。
这是判定直角三角形的根据之一、、1什么叫命题?命题由几部分组成?
命题的种类有几种?命题的一般形式如何?命题:“两直线平行,内错角相等.”题设是: ,
结论是: .内错角相等两直线平行内错角相等,两直线平行.这个命题的逆命题:互逆命题的题设和结论反过来.(1)两条直线平行,内错角相等.
(2)如果两个实数相等,那么它们的绝对值相等.
(3)全等三角形的对应角相等
(4)角的内部到角的两边距离相等的点在角的平分线上. .说出下列命题的逆命题.并这些命题的真假性.逆命题: 内错角相等,两条直线平行. 逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 逆命题:三个角对应相等的两个三角形是全等三角形. 逆命题:角平分线上的点到角两边的距离相等.感悟: 原命题成立时, 逆命题有时成立, 有时不成立一个命题是真命题,它逆命题却不一定是真命题.真命题假命题假命题真命题1、下列各组线段中,能够围成直角三角形的是 ( )
A、1、2、3 B、15、20、25
C、4、5、6 D、18、9、102、下列各组线段中,不能够围成直角三角形是 ( )
A、9、12、15 B、8、15、17
C、7、24、25 D、6、8、9BDCA、锐角三角形 B、钝角三角形
C、直角三角形 D、等边三角形4.解:(3)∵12+( )2=1+3=4,
22=4,
∴ 12+( )2=22.
∴这个三角形是直角三角形.(3)a=1,b=2,c= ; (4)a:b:c=3:4:5. 6.判断由a、b、c组成的三角形是不是直角三角形:(4)设a=3x, b=4x, c=5x,则
∵(3x)2+(4x )2=25x2,
(5x)2= 25x2,
∴ (3x)2+(4x )2 = (5x)2.
∴这个三角形是直角三角形.2.说出下列命题的逆命题.这些命题的逆命题成立吗?
(1)两条直线平行,内错角相等;
(2)如果两个实数相等,那么它们的绝对值相 等;
(3)全等三角形的对应角相等;
(4)到角的两边距离相等的点在角的平分线上.练习
