整式的加减全章复习课
图片预览









文档简介
课件30张PPT。
《整式加减》复习课
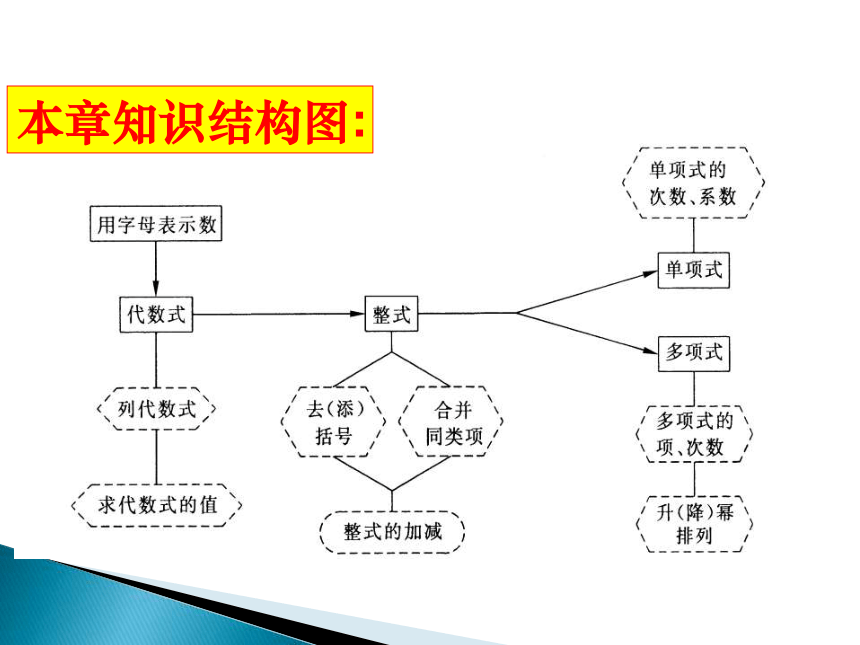
本章知识结构图:一、代数式:用加、减、乘(乘方)、除等运算符号把数或表示数的字母连接而成的式子,称为代数式。注意:代数式的书写要求以上代数式中,那些符合代数式的书写要求?特别地:单独的一个数或字母也是代数式 练习:1.代数式的定义:定义:单项式中的_________。次数:1.当单项式的系数是1或-1时,“1”通常省略不写。单项式:系数:数字与字母的乘积由_________________组成的代数式。
单独的______或________也是单项式。单项式中的__________________.数字因数所有字母的指数和一个数一个字母注意的问题:2.当式子分母中出现字母时不是单项式。3.圆周率π是常数,不要看成字母。4.当单项式的系数是带分数时,通常写成假分数。5.单项式的系数应包括它前面的性质符号。6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。定义:几个__________.常数项:多项式中_______________.多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
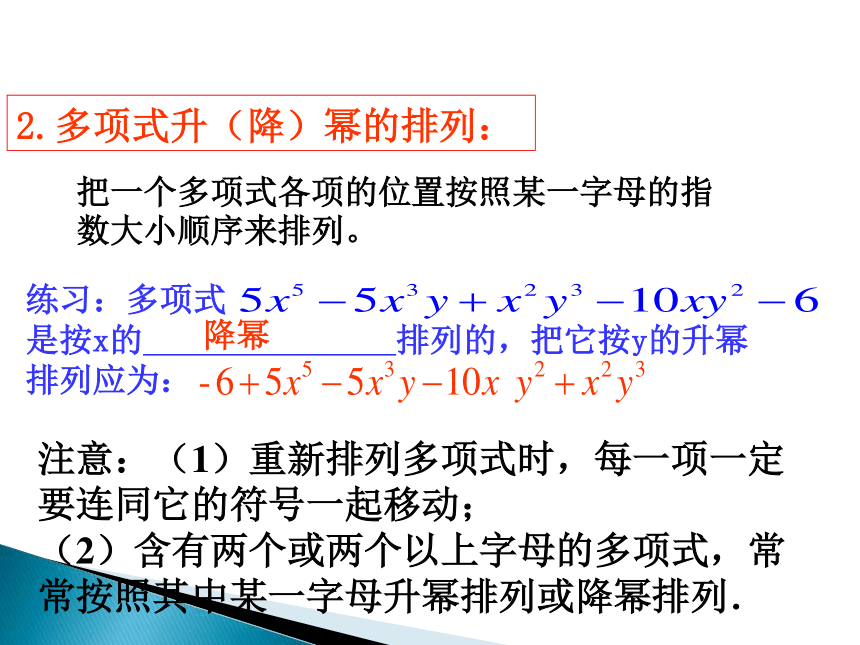
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。多项式单项式的和每一个单项式几项式不含字母的项多项式中次数最高的项的次数。注意的问题:2.多项式升(降)幂的排列:把一个多项式各项的位置按照某一字母的指数大小顺序来排列。练习:多项式 是按x的 排列的,把它按y的升幂排列应为: 降幂注意:(1)重新排列多项式时,每一项一定要连同它的符号一起移动;
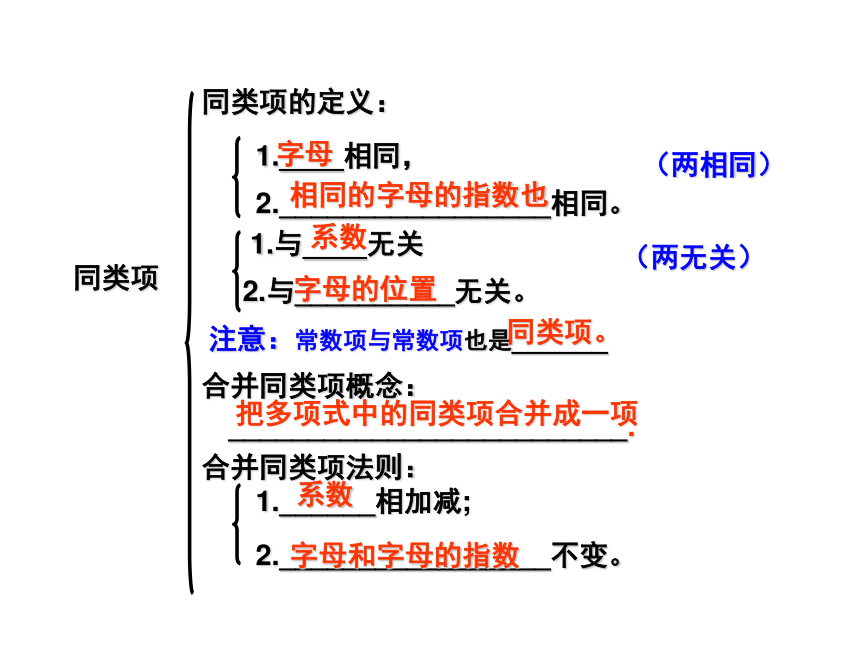
(2)含有两个或两个以上字母的多项式,常常按照其中某一字母升幂排列或降幂排列.同类项的定义:(两相同)合并同类项概念:_________________________.合并同类项法则:2._________________不变。2._________________相同。1.____相同,字母相同的字母的指数也1.______相加减;字母和字母的指数系数同类项注意:常数项与常数项也是______同类项。(两无关)2.与__________无关。1.与____无关系数 字母的位置把多项式中的同类项合并成一项2.若 与 是同类项,则m+n=___.4.若 ,则m+n-p=______543.若 与 的和是一个单项式,则 =___.-41.下列各式中,是同类项的是:___________① 与 ② 与 ③ 与 ④ 与 ⑤ 与 ⑥-125与③⑤⑥整式的加减混合运算步骤(有括号先去括号)1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.合并同类项。
4.按要求按“升”或“降”幂排列。 1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去(添)括号,看符号。是‘+’号,不变号,是‘-’号,全变号”一:去括号二:计算(按照先小括号,再中括号,最后大括号的顺序)判断下列各式是否正确:√××( )( )( )×( )去括号时,1,注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2,注意外面有系数的,各项都要乘以那个系数;一、概念中的易错题典型题二、运算中的易错题典型题易错点总结:1,单项式的定义例1,下列各式子中,是单项式的有______________(填序号)①、②、④、⑦注意:1,单个的字母或数字也是单项式;
2,用加减号把数字或字母连接在一起
的式子不是单项式;
3,只用乘号把数字或字母连接在一起
的式子仍是单项式;
4,当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)多项式的项数与次数例2 下列多项式次数为3的是( )C例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母14答案:二、运算过程中的易错题书写格式中的易错点例1、下列各个式子中,书写格式正确的是( )1、代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2、带分数与字母相乘,要写成假分数
3、代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4、系数一般写在字母的前面,且系数“1”往往会省略;F例2、 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。易错点:结果不进行化简,直接写点拨:结果中有 它们是同类项,应合并以保证最后的结果最简.正确的写法是例3 下列合并同类项的结果错误的有_______________.①、②、③、④、⑤注意:1,合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2,合并同类项后也要注意书写格式;
3,如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;0例4 合并同类项:小明的解法:(1)错在把所有项都当作同类项了;正确的解法:例5、 合并同类项:小明的解法:(2)错在把结合同类项时弄错了符号;正确的解法:总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。多重括号化简的易错题注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;“A+2B”类型的易错题:例1 若多项式 计算多项式A-2B;注意:列式时要先加上括号,再去括号;例2 一个多项式A加上 得 ,求这个多项式A?注意:我们在移项的时候是整体移项,不要漏了添上括号;化简下列式子:∴原式=-a-2[-(a+b)]-3(b-a)解:由题意知:a<0,b>0且|a|>|b|=-a+2[a+b]-3b+3a=-a+2a+2b-3b+3a=(-a+2a+3a)+(2b-3b)=4a-b例2.当x=1时, 则当x=-1时,解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7=-5-2例3、.如果关于x的多项式 的值与x
无关,则a的取值为_____.解:原式=由题意知,则:6a-6=0∴a=11补充两题:1、探索规律并填空:
(1) .....
。 思考:(2)计算: .2、小丽做一道数学题:“已知两个多项式A,B,B为4x2-5x-6,求A+B.”,小丽把A+B看成A-B计算结果是-7x2+10x+12.根据以上信息,你能求出A+B的结果吗?计算与求值:作业:实际问题(1)小明在实践课中做一个长方形模型,一边为3a+2b,另一边比它小a-b,则长方形的周长为多少?(2)大众超市出售一种商品其原价为a元,现三种调价方案: 1.先提价格上涨20%,再降价格20%
2. 先降价格上涨20%,再提价格20%
3. 先提价格上涨15%,再降价格15%
问用这三种方案调价结果是否一样?最后是不是都恢复了原价?
单独的______或________也是单项式。单项式中的__________________.数字因数所有字母的指数和一个数一个字母注意的问题:2.当式子分母中出现字母时不是单项式。3.圆周率π是常数,不要看成字母。4.当单项式的系数是带分数时,通常写成假分数。5.单项式的系数应包括它前面的性质符号。6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。定义:几个__________.常数项:多项式中_______________.多项式的次数:_________________________.
项: 组成多项式中的_____________.
有几项,就叫做_________.1.在确定多项式的项时,要连同它前面的符号,
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。多项式单项式的和每一个单项式几项式不含字母的项多项式中次数最高的项的次数。注意的问题:2.多项式升(降)幂的排列:把一个多项式各项的位置按照某一字母的指数大小顺序来排列。练习:多项式 是按x的 排列的,把它按y的升幂排列应为: 降幂注意:(1)重新排列多项式时,每一项一定要连同它的符号一起移动;
(2)含有两个或两个以上字母的多项式,常常按照其中某一字母升幂排列或降幂排列.同类项的定义:(两相同)合并同类项概念:_________________________.合并同类项法则:2._________________不变。2._________________相同。1.____相同,字母相同的字母的指数也1.______相加减;字母和字母的指数系数同类项注意:常数项与常数项也是______同类项。(两无关)2.与__________无关。1.与____无关系数 字母的位置把多项式中的同类项合并成一项2.若 与 是同类项,则m+n=___.4.若 ,则m+n-p=______543.若 与 的和是一个单项式,则 =___.-41.下列各式中,是同类项的是:___________① 与 ② 与 ③ 与 ④ 与 ⑤ 与 ⑥-125与③⑤⑥整式的加减混合运算步骤(有括号先去括号)1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.合并同类项。
4.按要求按“升”或“降”幂排列。 1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去(添)括号,看符号。是‘+’号,不变号,是‘-’号,全变号”一:去括号二:计算(按照先小括号,再中括号,最后大括号的顺序)判断下列各式是否正确:√××( )( )( )×( )去括号时,1,注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2,注意外面有系数的,各项都要乘以那个系数;一、概念中的易错题典型题二、运算中的易错题典型题易错点总结:1,单项式的定义例1,下列各式子中,是单项式的有______________(填序号)①、②、④、⑦注意:1,单个的字母或数字也是单项式;
2,用加减号把数字或字母连接在一起
的式子不是单项式;
3,只用乘号把数字或字母连接在一起
的式子仍是单项式;
4,当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)多项式的项数与次数例2 下列多项式次数为3的是( )C例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母14答案:二、运算过程中的易错题书写格式中的易错点例1、下列各个式子中,书写格式正确的是( )1、代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2、带分数与字母相乘,要写成假分数
3、代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4、系数一般写在字母的前面,且系数“1”往往会省略;F例2、 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。易错点:结果不进行化简,直接写点拨:结果中有 它们是同类项,应合并以保证最后的结果最简.正确的写法是例3 下列合并同类项的结果错误的有_______________.①、②、③、④、⑤注意:1,合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2,合并同类项后也要注意书写格式;
3,如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;0例4 合并同类项:小明的解法:(1)错在把所有项都当作同类项了;正确的解法:例5、 合并同类项:小明的解法:(2)错在把结合同类项时弄错了符号;正确的解法:总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。多重括号化简的易错题注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;“A+2B”类型的易错题:例1 若多项式 计算多项式A-2B;注意:列式时要先加上括号,再去括号;例2 一个多项式A加上 得 ,求这个多项式A?注意:我们在移项的时候是整体移项,不要漏了添上括号;化简下列式子:∴原式=-a-2[-(a+b)]-3(b-a)解:由题意知:a<0,b>0且|a|>|b|=-a+2[a+b]-3b+3a=-a+2a+2b-3b+3a=(-a+2a+3a)+(2b-3b)=4a-b例2.当x=1时, 则当x=-1时,解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7=-5-2例3、.如果关于x的多项式 的值与x
无关,则a的取值为_____.解:原式=由题意知,则:6a-6=0∴a=11补充两题:1、探索规律并填空:
(1) .....
。 思考:(2)计算: .2、小丽做一道数学题:“已知两个多项式A,B,B为4x2-5x-6,求A+B.”,小丽把A+B看成A-B计算结果是-7x2+10x+12.根据以上信息,你能求出A+B的结果吗?计算与求值:作业:实际问题(1)小明在实践课中做一个长方形模型,一边为3a+2b,另一边比它小a-b,则长方形的周长为多少?(2)大众超市出售一种商品其原价为a元,现三种调价方案: 1.先提价格上涨20%,再降价格20%
2. 先降价格上涨20%,再提价格20%
3. 先提价格上涨15%,再降价格15%
问用这三种方案调价结果是否一样?最后是不是都恢复了原价?
