5.1.1相交线课件
图片预览





文档简介
课件18张PPT。5.1 相交线(5.1.1 相交线)学习目标:
(1)理解邻补角和对顶角的概念.
(2)掌握“对顶角相等”的性质.
重点:
对顶角相等的性质.
难点:
邻补角、对顶角性质的应用。一、问题引入(1分钟)棋盘上的横线和竖线大桥上的钢梁和钢索 学校操场上的双杠,教室中课桌面、黑板面相邻的两边与相对的两条边……都给我们以相交线平行线的形象 预习课本第2页至第3页练习,思考以下问题:
1、两条直线相交可以出现___种形式的角,它们分别是_______、________。
2、邻补角有两个特点,分别是_____、____;对顶角有两个特点,分别是____、____。
3、邻补角、对顶角分别具有什么样的性质?
4、在例1的学习过程中,你体会到什么?二、问题引领(10分钟)
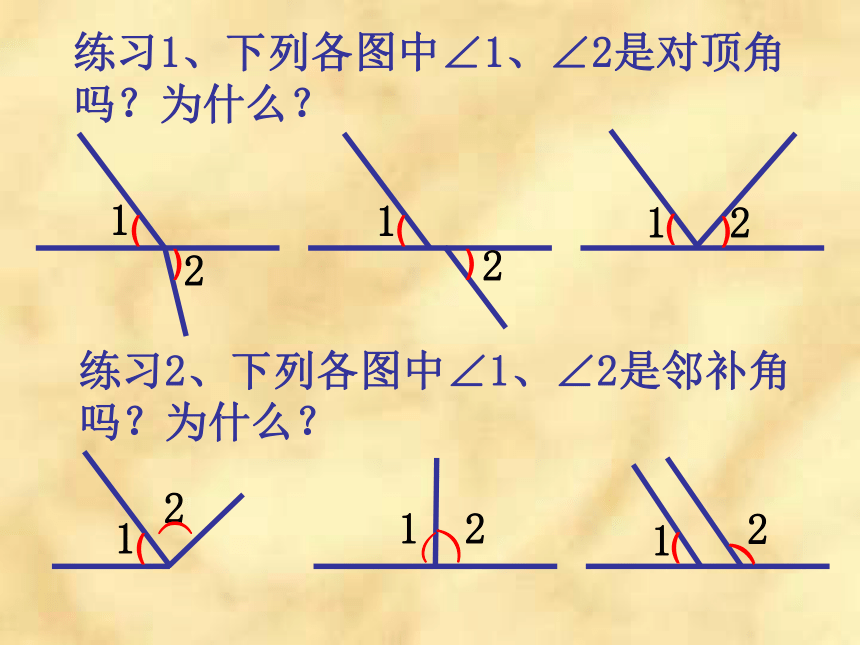
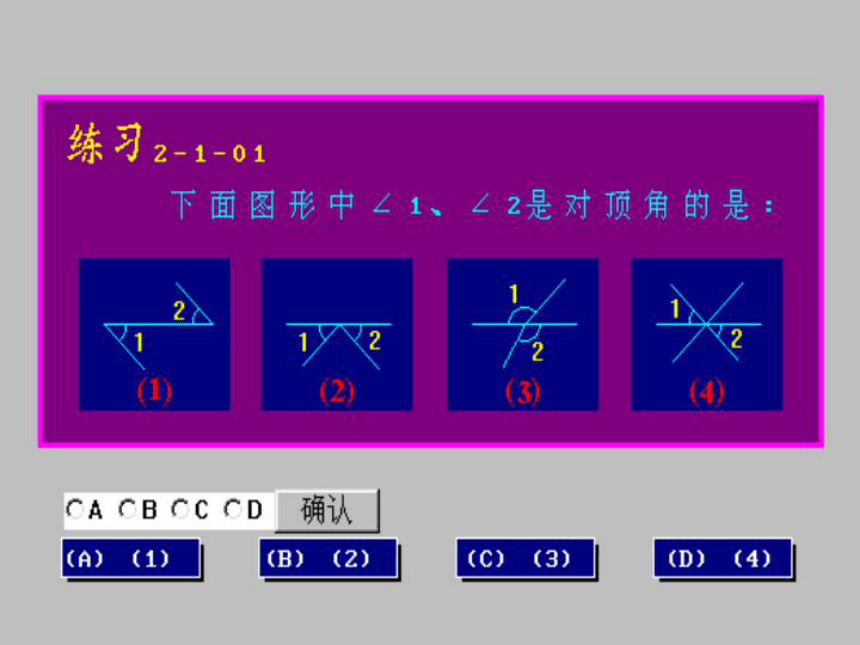
三、合作探究(15分钟)1练习1、下列各图中∠1、∠2是对顶角吗?为什么?21212)((())1练习2、下列各图中∠1、∠2是邻补角吗?为什么?21212)((()( 3、如图,三条直线AB ,CD ,EF相交于
点O,∠AOE的对顶角是 ,
∠EOD的邻补角是 .
O细心观察,归纳定义∠FOB∠FOD、∠COEab)(1342)(例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠ 4的度数。(对顶角相等)∵∠3=∠1∠1=40°( )已知∴∠3=40°解:(等量代换)∴∠2=180°—∠1=140°∴∠4=∠2=140°(对顶角相等)(邻补角的定义)变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠ = - = °2、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。3、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.ACBDE1一两无数AOC∠AOCDOB180°30°50对顶角相等已知二、 填空801、右图中∠AOC的对顶角是 ,
邻补角是 .∠DOB∠AOD和∠COB2))O 对顶角相等. 对顶角的性质:OABCD)(1342)( 为什么?已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3 (或∠2=∠4)。 解:∵直线AB与CD相交于O点,∴∠1+∠2=180°
∠2+∠3=180(邻补角定义)∴∠1=∠3(等角的补角相等)2、求证: 对顶角相等.达标测试(5分钟)一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A。∠AOC和∠BOE是对顶角;
B。∠COE和∠AOD是对顶角;
C。∠BOC和∠AOD是对顶角;
D。∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,
那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。ABCDOE×√√CC三、填空(每空3分)
如图1,直线AB、CD交EF于点
G、H,∠2=∠3,∠1=70度。求
∠4的度数。
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°—∠ = ( 的定义)ACDBEFGH1234图11对顶角相等已知70°∠2=∠370 °等量代换3110 °邻补角解:∵∠AOC=50°(已知)
∴∠AOD=180°—∠AOC=180°—50°
=130°(邻补角的定义)
∵OE平分∠AOD(已知)
∴∠DOE=1/2∠AOD=130°÷2=65°(角
平分线的定义)四、解答题(5分钟)
直线AB、CD交于点O,OE是∠AOD的平分线,已知∠AOC=50°。求∠DOE的度数。ABCDOE图2例2 如图,直线a,b相交于点O,∠1 = ,
求∠2 ,∠3 ,∠4 的度数.5.动脑思考,变式训练O变式2 若∠2是∠1的 3.5倍,
求各个角的度数.变式1 若∠1+∠3= 80o ,
求各个角的度数.变式3 若 ?1: ?2 = 2: 7 ,
求各个角的度数.(5分钟)归纳小结 (4分钟) 对顶
角相
等
邻补
角互
补 ②有公共顶点;③没有公共边①两条直线相交形成的角; ①两条直线相交而成;②有公共顶点;③有一条公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,
对顶角只有两对
邻补角有四对 ①有无公共边作业: 课本
第8页 2(必做)
第35页 2(选做)教学反思:
进一步提高学生综合识图能力。
(1)理解邻补角和对顶角的概念.
(2)掌握“对顶角相等”的性质.
重点:
对顶角相等的性质.
难点:
邻补角、对顶角性质的应用。一、问题引入(1分钟)棋盘上的横线和竖线大桥上的钢梁和钢索 学校操场上的双杠,教室中课桌面、黑板面相邻的两边与相对的两条边……都给我们以相交线平行线的形象 预习课本第2页至第3页练习,思考以下问题:
1、两条直线相交可以出现___种形式的角,它们分别是_______、________。
2、邻补角有两个特点,分别是_____、____;对顶角有两个特点,分别是____、____。
3、邻补角、对顶角分别具有什么样的性质?
4、在例1的学习过程中,你体会到什么?二、问题引领(10分钟)
三、合作探究(15分钟)1练习1、下列各图中∠1、∠2是对顶角吗?为什么?21212)((())1练习2、下列各图中∠1、∠2是邻补角吗?为什么?21212)((()( 3、如图,三条直线AB ,CD ,EF相交于
点O,∠AOE的对顶角是 ,
∠EOD的邻补角是 .
O细心观察,归纳定义∠FOB∠FOD、∠COEab)(1342)(例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠ 4的度数。(对顶角相等)∵∠3=∠1∠1=40°( )已知∴∠3=40°解:(等量代换)∴∠2=180°—∠1=140°∴∠4=∠2=140°(对顶角相等)(邻补角的定义)变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠ = - = °2、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。3、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.ACBDE1一两无数AOC∠AOCDOB180°30°50对顶角相等已知二、 填空801、右图中∠AOC的对顶角是 ,
邻补角是 .∠DOB∠AOD和∠COB2))O 对顶角相等. 对顶角的性质:OABCD)(1342)( 为什么?已知:直线AB与CD相交于O点(如图),
求证:∠1=∠3 (或∠2=∠4)。 解:∵直线AB与CD相交于O点,∴∠1+∠2=180°
∠2+∠3=180(邻补角定义)∴∠1=∠3(等角的补角相等)2、求证: 对顶角相等.达标测试(5分钟)一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A。∠AOC和∠BOE是对顶角;
B。∠COE和∠AOD是对顶角;
C。∠BOC和∠AOD是对顶角;
D。∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,
那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。ABCDOE×√√CC三、填空(每空3分)
如图1,直线AB、CD交EF于点
G、H,∠2=∠3,∠1=70度。求
∠4的度数。
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°—∠ = ( 的定义)ACDBEFGH1234图11对顶角相等已知70°∠2=∠370 °等量代换3110 °邻补角解:∵∠AOC=50°(已知)
∴∠AOD=180°—∠AOC=180°—50°
=130°(邻补角的定义)
∵OE平分∠AOD(已知)
∴∠DOE=1/2∠AOD=130°÷2=65°(角
平分线的定义)四、解答题(5分钟)
直线AB、CD交于点O,OE是∠AOD的平分线,已知∠AOC=50°。求∠DOE的度数。ABCDOE图2例2 如图,直线a,b相交于点O,∠1 = ,
求∠2 ,∠3 ,∠4 的度数.5.动脑思考,变式训练O变式2 若∠2是∠1的 3.5倍,
求各个角的度数.变式1 若∠1+∠3= 80o ,
求各个角的度数.变式3 若 ?1: ?2 = 2: 7 ,
求各个角的度数.(5分钟)归纳小结 (4分钟) 对顶
角相
等
邻补
角互
补 ②有公共顶点;③没有公共边①两条直线相交形成的角; ①两条直线相交而成;②有公共顶点;③有一条公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,
对顶角只有两对
邻补角有四对 ①有无公共边作业: 课本
第8页 2(必做)
第35页 2(选做)教学反思:
进一步提高学生综合识图能力。
