1.2.1 代入消元法课件
图片预览





文档简介
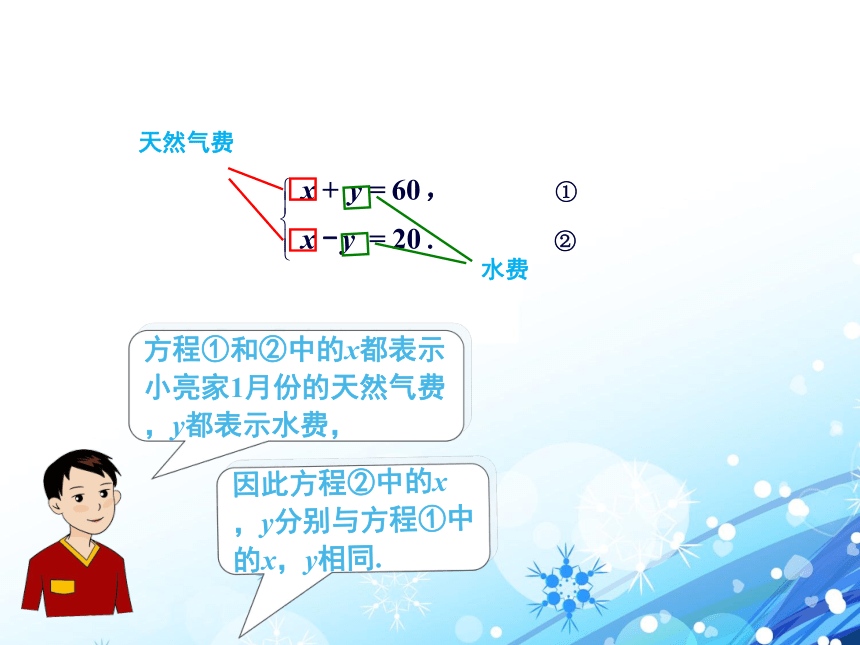
课件18张PPT。二元一次方程组的解法1.2——1.2.1 代入消元法桂阳县樟市镇团结墟中心校执教老师:刘上忠 现在我们来解决1月份的天然气费和水费各是多少元的问题. 首先,想一想如何解二元一次方程组 我会解一元一次方程,可是现在方程①和②都有两个未知数……方程①和②中的x都表示小亮家1月份的天然气费,y都表示水费,因此方程②中的x,y分别与方程①中的x,y相同.天然气费水费啊!这个一元一次方程我会解.解方程④,得y= .
把y的值代入③,得x= . 2040因此原方程组的解是由②式可得
x=y+20, ③
于是可以把③代入①式得
(y+20)+y=60. ④ 同桌同学讨论,解二元一次方程组的基本
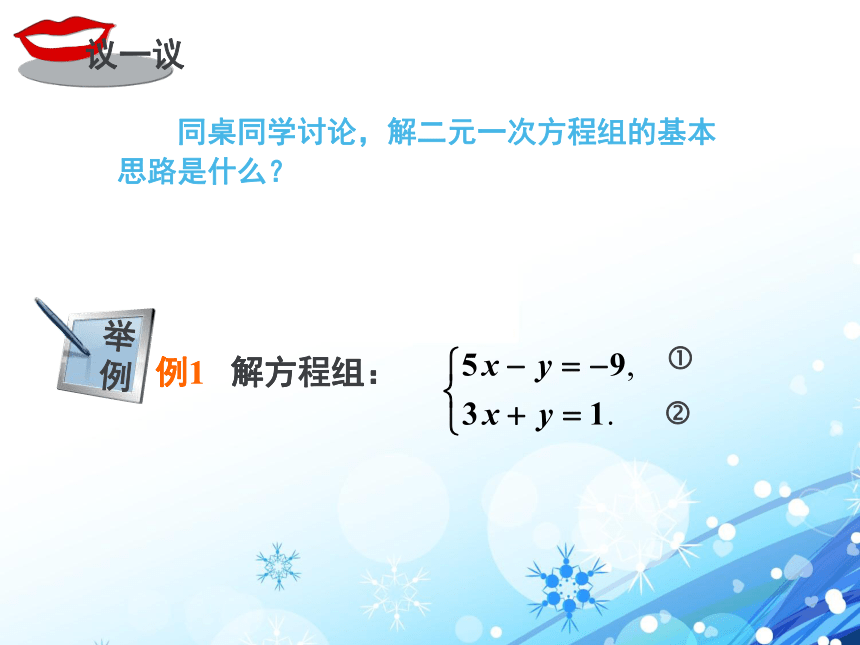
思路是什么?举
例例1 解方程组:例1 解方程组:??解得 x = -1.把x=-1代入③ ,得
y = 4.每位同学把x=-1,y=4代入例1的方程①和②中,检验上面算得对不对.解
答??因此原方程组的解是例2 解方程组:举
例把y=2代入③式 ,得 x = 3因此原方程组的解是把③代入 ② 式,得解
答 解二元一次方程组的基本思路是:消去一个未知数(简称为消元),得到一个一元一次方程,然后解这个一元一次方程. 在上面的几个例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程. 这种解方程组的方法叫做代入消元法,简称为代入法.用代入消元法解下列方程组:解:把②式代入 ①式,得3x+2(2x-1)= 5. ③解得 x = 1.把x=1代入②式 ,得
y = 1.因此原方程组的解是解
答解: 由①式得, y=3x+1. ③把③式代入②式 ,得2x+3(3x+1)-3=0, x =0.把x=0代入③式 ,得 y = 1.因此原方程组的解是解
答例1 方程组 的解是 . 方程组 的解是 .例2回顾本节课的学习过程,并回答以下问题:(1)代入法解二元一次方程组大致有哪些步骤?答:步骤包括变形、代入、解方程、回代、写成解的形式等等.(2)解二元一次方程组的核心思想是什么?答:核心思想是“消元思想”.(3)在探究解法的过程中用到了什么思想方法,你还有哪些收获?答:用到了转化、划归的思想,即把“二元”化归为“一元” .1解下列二元一次方程组:1、教科书第13页习题1.2A组第3题:
当 x=2,-2时,代数式 kx+b的值分别是-2,-4. 求 k、b的值.2、教科书第13页习题1.2B组第2题:
有一个两位数,个位上的数比十位上的数大 5, 如果把这两个数的位置进行对换,那么所得的新数与原数的和是143. 求这个两位数.
把y的值代入③,得x= . 2040因此原方程组的解是由②式可得
x=y+20, ③
于是可以把③代入①式得
(y+20)+y=60. ④ 同桌同学讨论,解二元一次方程组的基本
思路是什么?举
例例1 解方程组:例1 解方程组:??解得 x = -1.把x=-1代入③ ,得
y = 4.每位同学把x=-1,y=4代入例1的方程①和②中,检验上面算得对不对.解
答??因此原方程组的解是例2 解方程组:举
例把y=2代入③式 ,得 x = 3因此原方程组的解是把③代入 ② 式,得解
答 解二元一次方程组的基本思路是:消去一个未知数(简称为消元),得到一个一元一次方程,然后解这个一元一次方程. 在上面的几个例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程. 这种解方程组的方法叫做代入消元法,简称为代入法.用代入消元法解下列方程组:解:把②式代入 ①式,得3x+2(2x-1)= 5. ③解得 x = 1.把x=1代入②式 ,得
y = 1.因此原方程组的解是解
答解: 由①式得, y=3x+1. ③把③式代入②式 ,得2x+3(3x+1)-3=0, x =0.把x=0代入③式 ,得 y = 1.因此原方程组的解是解
答例1 方程组 的解是 . 方程组 的解是 .例2回顾本节课的学习过程,并回答以下问题:(1)代入法解二元一次方程组大致有哪些步骤?答:步骤包括变形、代入、解方程、回代、写成解的形式等等.(2)解二元一次方程组的核心思想是什么?答:核心思想是“消元思想”.(3)在探究解法的过程中用到了什么思想方法,你还有哪些收获?答:用到了转化、划归的思想,即把“二元”化归为“一元” .1解下列二元一次方程组:1、教科书第13页习题1.2A组第3题:
当 x=2,-2时,代数式 kx+b的值分别是-2,-4. 求 k、b的值.2、教科书第13页习题1.2B组第2题:
有一个两位数,个位上的数比十位上的数大 5, 如果把这两个数的位置进行对换,那么所得的新数与原数的和是143. 求这个两位数.
