人教版数学8年级上册 13.3.1 等腰三角形 学案(无答案)
文档属性
| 名称 | 人教版数学8年级上册 13.3.1 等腰三角形 学案(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 86.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 20:13:33 | ||
图片预览


文档简介
等腰三角形
【学习安排】
2课时
【第一课时】
【学习目标】
1.理解掌握等腰三角形的性质。运用等腰三角形性质进行证明和计算。
2.通过实践、观察、证明等腰三角形的性质,发展推理能力,培养分析、归纳问题的能力。
3.培养对图形的观察、发现,激发好奇心和求知欲,并在运用数学知识解答问题的活动中取得成功的体验。
【学习重难点】
1.等腰三角形的性质及应用。
2.等腰三角形的证明。
【学习过程】
一、预习自测。
1.下列图形不一定是轴对称图形的是( )。
A.圆 B.长方形 C.线段 D.三角形
2.怎样的三角形是轴对称图形?
3.有两边相等的三角形叫_____,相等的两边叫_____,另一边叫_____两腰的夹角叫_____,腰和底边的夹角叫_____。
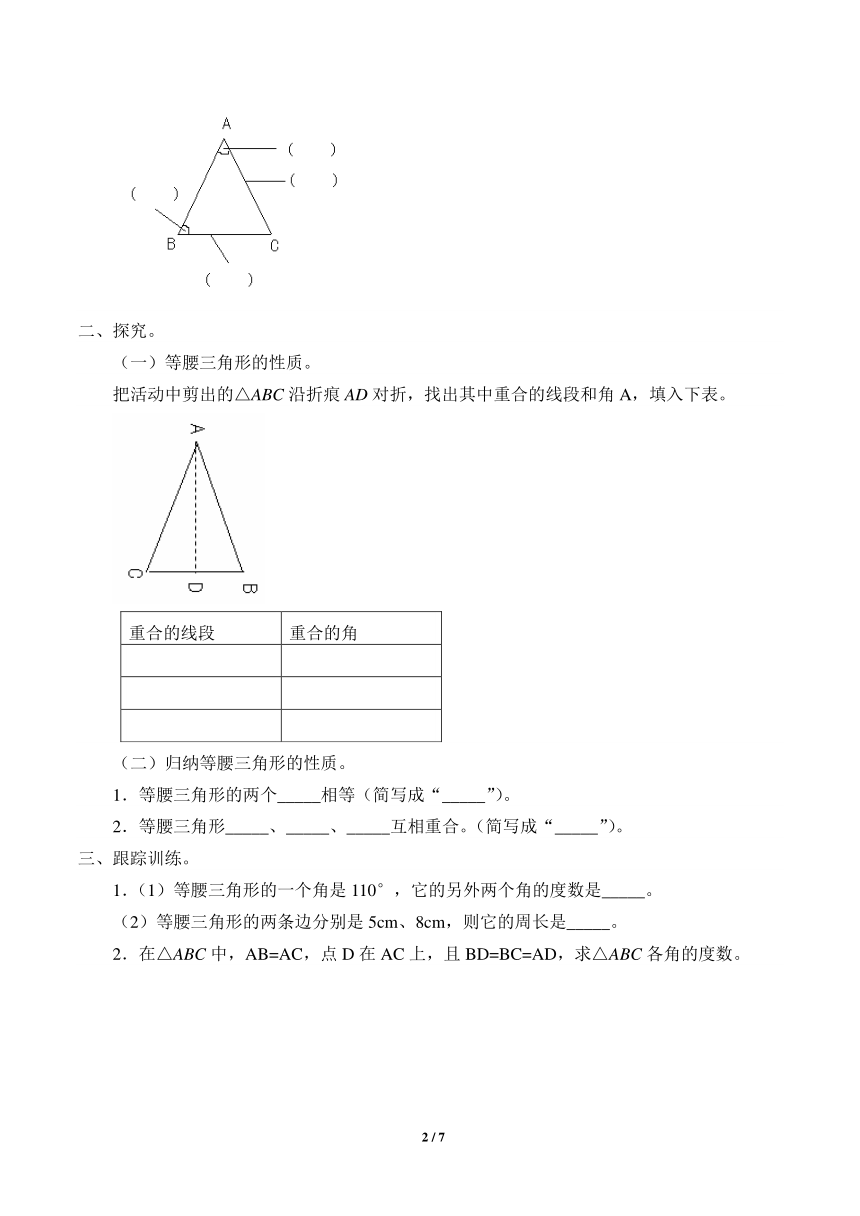
4.如图,在△ABC中,AB=AC,标出各部分名称。
二、探究。
(一)等腰三角形的性质。
把活动中剪出的△ABC沿折痕AD对折,找出其中重合的线段和角A,填入下表。
重合的线段 重合的角
(二)归纳等腰三角形的性质。
1.等腰三角形的两个_____相等(简写成“_____”)。
2.等腰三角形_____、_____、_____互相重合。(简写成“_____”)。
三、跟踪训练。
1.(1)等腰三角形的一个角是110°,它的另外两个角的度数是_____。
(2)等腰三角形的两条边分别是5cm、8cm,则它的周长是_____。
2.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
3.已知一个等腰三角形两个内角的度数之比为1:4,则这个等腰三角形顶角的度数为_____。
4.等腰三角形一腰上的高和另一腰的夹角为40o,则底角为_____。
5.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数。
6.如图,CA=CB,DF=DB,AE=AD,求∠A的度数。
7.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证BD=CE。
8.如图4,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为点M,求证:CM=DM。
【第二课时】
【学习目标】
1.理解掌握等腰三角形的判定运用等腰三角形判定进行证明和计算。
2.通过推理证明等腰三角形的判定定理,发展推理能力,培养分析、归纳问题的能力。
3.观察发现等腰三角形的判定方法,获得成功的感受,并在这个过程中体验学习的乐趣。
【学习重难点】
1.等腰三角形的判定定理。
2.等腰三角形判定定理的证明。
【学习过程】
一、预习自测。
1.等腰三角形的两边长分别为4,8,则周长为_____。
2.等腰三角形的周长为14,其中一边长为6,则另两边分别为_____。
3.等腰三角形的一个角为70°,则另外两个角的度数是_____。
4.等腰三角形的一个角为120°则另外两个角的度数是_____。
5.如图,在△ABC中,AB=AC,
(1)若AD平分∠BAC,那么_____、_____。
(2)若BD=CD,那么_____、_____。
(3)若AD⊥BC,那么_____、_____。
二、探究。
(一)等腰三角形的判定。
思考:(1)如图,位于在海上A.B两处的两艘救生船接到O处遇险船只的报警,当
测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点
(不考虑风浪因素)?
(2)我们把这个问题一般化,在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABO中,∠A=∠B求证:AO=AO
(二)等腰三角形的判定方法。
如果一个三角形有两个角相等,那么这两个角所对的_____也相等(简写成_____)。
三、跟踪训练。
1.如图,AD∥BC,BD平分∠ABC.求证:AB=AD。
2.如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。
3.如图,在△ABC中,AB=AC,∠B=36O,D、E是BC上的两点,且∠ADE=∠AED=2∠BAD,则图中的等腰三角形共有( )个。
A.3个 B.4个 C.5个 D.6个
4.如图,∠A=∠B,CE∥DA,CE交AB于E,求证△CEB是等腰三角形。
5.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
6.如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F求证:EF=EB+FC。
7.如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点。证明△OAE≌△OBE。
7 / 7
【学习安排】
2课时
【第一课时】
【学习目标】
1.理解掌握等腰三角形的性质。运用等腰三角形性质进行证明和计算。
2.通过实践、观察、证明等腰三角形的性质,发展推理能力,培养分析、归纳问题的能力。
3.培养对图形的观察、发现,激发好奇心和求知欲,并在运用数学知识解答问题的活动中取得成功的体验。
【学习重难点】
1.等腰三角形的性质及应用。
2.等腰三角形的证明。
【学习过程】
一、预习自测。
1.下列图形不一定是轴对称图形的是( )。
A.圆 B.长方形 C.线段 D.三角形
2.怎样的三角形是轴对称图形?
3.有两边相等的三角形叫_____,相等的两边叫_____,另一边叫_____两腰的夹角叫_____,腰和底边的夹角叫_____。
4.如图,在△ABC中,AB=AC,标出各部分名称。
二、探究。
(一)等腰三角形的性质。
把活动中剪出的△ABC沿折痕AD对折,找出其中重合的线段和角A,填入下表。
重合的线段 重合的角
(二)归纳等腰三角形的性质。
1.等腰三角形的两个_____相等(简写成“_____”)。
2.等腰三角形_____、_____、_____互相重合。(简写成“_____”)。
三、跟踪训练。
1.(1)等腰三角形的一个角是110°,它的另外两个角的度数是_____。
(2)等腰三角形的两条边分别是5cm、8cm,则它的周长是_____。
2.在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
3.已知一个等腰三角形两个内角的度数之比为1:4,则这个等腰三角形顶角的度数为_____。
4.等腰三角形一腰上的高和另一腰的夹角为40o,则底角为_____。
5.如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数。
6.如图,CA=CB,DF=DB,AE=AD,求∠A的度数。
7.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证BD=CE。
8.如图4,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为点M,求证:CM=DM。
【第二课时】
【学习目标】
1.理解掌握等腰三角形的判定运用等腰三角形判定进行证明和计算。
2.通过推理证明等腰三角形的判定定理,发展推理能力,培养分析、归纳问题的能力。
3.观察发现等腰三角形的判定方法,获得成功的感受,并在这个过程中体验学习的乐趣。
【学习重难点】
1.等腰三角形的判定定理。
2.等腰三角形判定定理的证明。
【学习过程】
一、预习自测。
1.等腰三角形的两边长分别为4,8,则周长为_____。
2.等腰三角形的周长为14,其中一边长为6,则另两边分别为_____。
3.等腰三角形的一个角为70°,则另外两个角的度数是_____。
4.等腰三角形的一个角为120°则另外两个角的度数是_____。
5.如图,在△ABC中,AB=AC,
(1)若AD平分∠BAC,那么_____、_____。
(2)若BD=CD,那么_____、_____。
(3)若AD⊥BC,那么_____、_____。
二、探究。
(一)等腰三角形的判定。
思考:(1)如图,位于在海上A.B两处的两艘救生船接到O处遇险船只的报警,当
测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点
(不考虑风浪因素)?
(2)我们把这个问题一般化,在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABO中,∠A=∠B求证:AO=AO
(二)等腰三角形的判定方法。
如果一个三角形有两个角相等,那么这两个角所对的_____也相等(简写成_____)。
三、跟踪训练。
1.如图,AD∥BC,BD平分∠ABC.求证:AB=AD。
2.如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。
3.如图,在△ABC中,AB=AC,∠B=36O,D、E是BC上的两点,且∠ADE=∠AED=2∠BAD,则图中的等腰三角形共有( )个。
A.3个 B.4个 C.5个 D.6个
4.如图,∠A=∠B,CE∥DA,CE交AB于E,求证△CEB是等腰三角形。
5.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
6.如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F求证:EF=EB+FC。
7.如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点。证明△OAE≌△OBE。
7 / 7
