人教版数学8年级上册 13.3.1 等腰三角形 学案(含答案)
文档属性
| 名称 | 人教版数学8年级上册 13.3.1 等腰三角形 学案(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 322.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 20:26:22 | ||
图片预览


文档简介
等腰三角形(3)
班级: 组号: 姓名::
一、旧知回顾
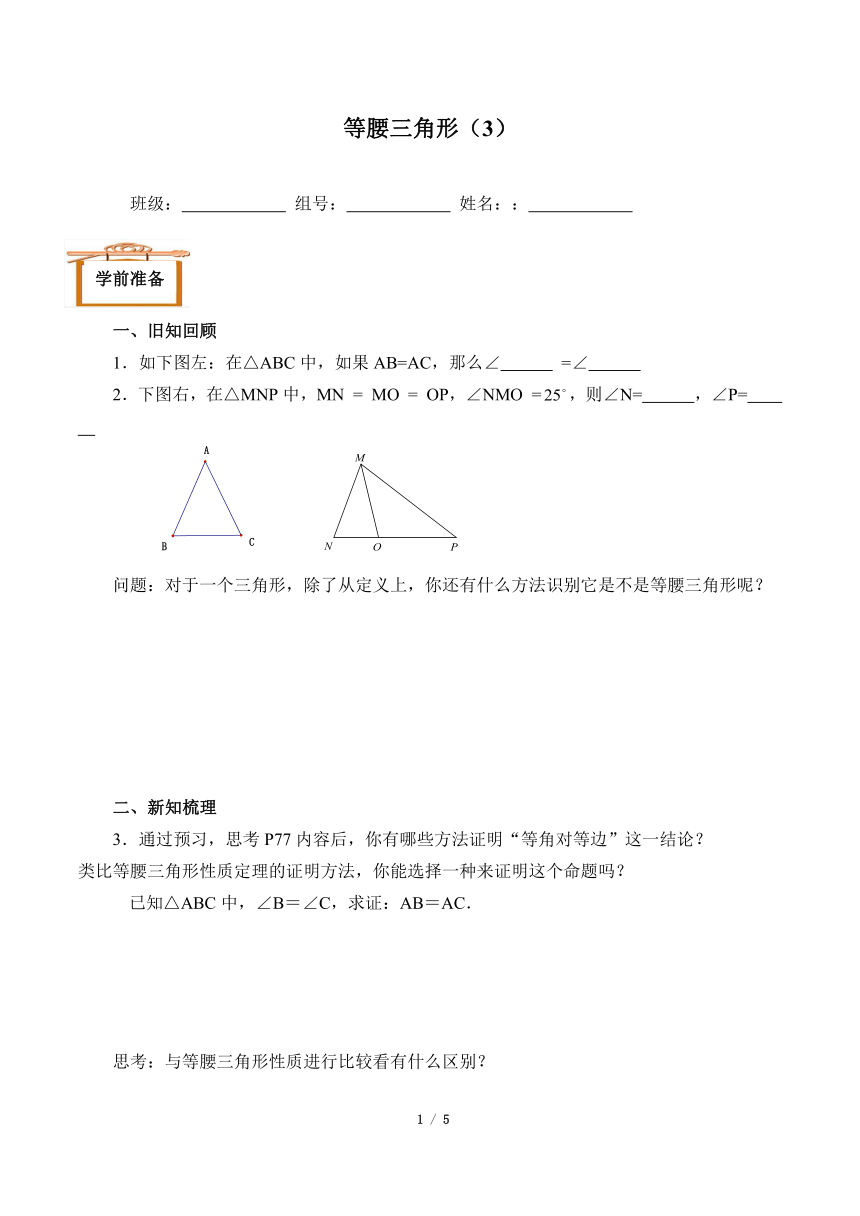
1.如下图左:在△ABC中,如果AB=AC,那么∠ =∠
2.下图右,在△MNP中,MN = MO = OP,∠NMO =,则∠N= ,∠P=
问题:对于一个三角形,除了从定义上,你还有什么方法识别它是不是等腰三角形呢?
二、新知梳理
3.通过预习,思考P77内容后,你有哪些方法证明“等角对等边”这一结论?
类比等腰三角形性质定理的证明方法,你能选择一种来证明这个命题吗?
已知△ABC中,∠B=∠C,求证:AB=AC.
思考:与等腰三角形性质进行比较看有什么区别?
4.学习例3的内容,边看边操作,体会已知底边和底边上的高,用尺规作等腰三角形的方法。
如:已知△ABC的底边BC和底边上的高AD,BC=4cm,AD=3cm,求作等腰三角形ABC。(尺规作图,不用写作图过程,但要保留作图痕迹)
三、试一试
5.如图,AC和BD相交于点O,且AB∥DC,。求证:。
由此也可得出把一张矩形的纸沿对角线折叠,重合部分是一个 三角形。
★通过预习你还有什么困惑?
一、课堂活动、记录
1.用什么方法来证明“等角对等边”的这一判定。
2.等角对等边的应用。
3.尺规作图(已知等腰三角形底边和底边上的高,用尺规作等腰三角形的方法)。
二、精练反馈
A组:
1.如图,∠A=36 ,,。则= ,
= ,图中的等腰三角形有 。
B组:
2.如图,已知在五边形ABCDE中,,BC=ED,。求证:AB=AE。
三、课堂小结
1.等腰三角形的判定方法有哪几种?
2.结合本节课的学习,谈谈等腰三角形性质和判定的区别和联系。
四、拓展延伸(选做题)
1.如图,在△ABC中,AB=AC,直线DF交AB于D、AC的延长线于点F、BC于点E,若BD=CF,你能证明E是DF的中点吗?
【答案】
【学前准备】
1.B C
2.77.5° 38.75° 答:通过等角对等边识别等腰三角形
3.略
4.略
5.解:∵AB∥DC ∴∠C=∠A,∠B=∠D
又∵OA=OB ∴∠A=∠B
∴∠C=∠D ∴OC=OD
等腰
【课堂探究】
课堂活动、记录
略
精练反馈
1.72° 36° △ABD,△BCD,△ABC
2.证明:∵
∴AC=AD
又∵
在Rt△ABC和Rt△AED中
∴Rt△ABC≌Rt△AED ∴AB=AE
课堂小结
略
拓展延伸
证明:如图,过点D作DG∥AC交BC于G
∴∠ACB=∠BGD,∠F=∠EDG
∵AB=AC,∴∠B=∠ACB
∴∠B=∠BGD
∴BD=GD
又∵BD=CF
∴GD=CF
∵在△CEF和△GED中,
∴△CEF≌△GED(AAS)
∴DE=EF
1 / 6
班级: 组号: 姓名::
一、旧知回顾
1.如下图左:在△ABC中,如果AB=AC,那么∠ =∠
2.下图右,在△MNP中,MN = MO = OP,∠NMO =,则∠N= ,∠P=
问题:对于一个三角形,除了从定义上,你还有什么方法识别它是不是等腰三角形呢?
二、新知梳理
3.通过预习,思考P77内容后,你有哪些方法证明“等角对等边”这一结论?
类比等腰三角形性质定理的证明方法,你能选择一种来证明这个命题吗?
已知△ABC中,∠B=∠C,求证:AB=AC.
思考:与等腰三角形性质进行比较看有什么区别?
4.学习例3的内容,边看边操作,体会已知底边和底边上的高,用尺规作等腰三角形的方法。
如:已知△ABC的底边BC和底边上的高AD,BC=4cm,AD=3cm,求作等腰三角形ABC。(尺规作图,不用写作图过程,但要保留作图痕迹)
三、试一试
5.如图,AC和BD相交于点O,且AB∥DC,。求证:。
由此也可得出把一张矩形的纸沿对角线折叠,重合部分是一个 三角形。
★通过预习你还有什么困惑?
一、课堂活动、记录
1.用什么方法来证明“等角对等边”的这一判定。
2.等角对等边的应用。
3.尺规作图(已知等腰三角形底边和底边上的高,用尺规作等腰三角形的方法)。
二、精练反馈
A组:
1.如图,∠A=36 ,,。则= ,
= ,图中的等腰三角形有 。
B组:
2.如图,已知在五边形ABCDE中,,BC=ED,。求证:AB=AE。
三、课堂小结
1.等腰三角形的判定方法有哪几种?
2.结合本节课的学习,谈谈等腰三角形性质和判定的区别和联系。
四、拓展延伸(选做题)
1.如图,在△ABC中,AB=AC,直线DF交AB于D、AC的延长线于点F、BC于点E,若BD=CF,你能证明E是DF的中点吗?
【答案】
【学前准备】
1.B C
2.77.5° 38.75° 答:通过等角对等边识别等腰三角形
3.略
4.略
5.解:∵AB∥DC ∴∠C=∠A,∠B=∠D
又∵OA=OB ∴∠A=∠B
∴∠C=∠D ∴OC=OD
等腰
【课堂探究】
课堂活动、记录
略
精练反馈
1.72° 36° △ABD,△BCD,△ABC
2.证明:∵
∴AC=AD
又∵
在Rt△ABC和Rt△AED中
∴Rt△ABC≌Rt△AED ∴AB=AE
课堂小结
略
拓展延伸
证明:如图,过点D作DG∥AC交BC于G
∴∠ACB=∠BGD,∠F=∠EDG
∵AB=AC,∴∠B=∠ACB
∴∠B=∠BGD
∴BD=GD
又∵BD=CF
∴GD=CF
∵在△CEF和△GED中,
∴△CEF≌△GED(AAS)
∴DE=EF
1 / 6
