反比例函数 导学案(共九课时)
图片预览




文档简介
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1.1反比例函数的意义 第 1 周 第 1 课时 课型 新授课
学习目标与重难点 学习目标:1、理解并掌握反比例函数的概念。2、能判断一个给定的函数是否为反比例函数,并会用待定系数法求函数解析式。学习重点:理解反比例函数的概念,能根据已知条件写出函数解析式学习难点:理解反比例函数的概念。
课前准备回忆一下什么是正比例函数、一次函数?它们的一般形式是怎样的?探究新知问题提出:电流I、电阻R、电压U之间满足关系式U=IR,当U=220V时,(1)你能用含有R的代数式表示I吗?(2)利用写出的关系式完成下表:R/Ω20406080100I/A当R越来越大时,I怎样变化?当R越来越小呢?(3)变量I是R的函数吗?为什么?学生小组合作讨论。概念:如果两个变量x,y之间的关系可以表示成 的形式,那么y是x的 函数,反比例函数的自变量x有什么条件?新知应用1.下列问题中,变量间的对应关系可用怎样的函数关系式表示?这些函数有什么共同特点?(1)京沪线铁路全程为1463km,乘坐某次列车所用时间t(单位:h)随该列车平均速度v(单位:km/h)的变化而变化;_________________(2)某住宅小区要种植一个面积为1000m2的矩形草坪,草坪的长为y随宽x的变化;_________________(3)已知北京市的总面积为1.68×104平方千米,人均占有的土地面积S(平方千米/人)随全市总人口数n(单位:人)的变化而变化。_________________上面的函数关系式,都具有_____________的形式,其中_________是常数。 学生回忆旧知小组合作,探究反比例函数变量的相依关系,领会其概念。
2.一个矩形的面积为20,相邻的两条边长分别为xcm和ycm。那么变量y是变量x的函数吗?为什么?3.y是x的反比例函数,下表给出了x与y的一些值:x-2-113…y2-1……(1)写出这个反比例函数的表达式;(2)根据函数表达式完成上表。三、当堂检测:1.下列等式中,哪些是反比例函数(1) (2) (3)xy=21 (4) (5)(6) (7)y=x-42.当m取什么值时,函数是反比例函数?3.苹果每千克x元,花10元钱可买y千克的苹果,则y与x之间的函数关系式为 4.若函数是反比例函数,则m的取值是 5.矩形的面积为4,一条边的长为x,另一条边的长为y,则y与x的函数解析式为 6.已知y与x成反比例,且当x=-2时,y=3,则y与x之间的函数关系式是 ,当x=-3时,y= 7.函数中自变量x的取值范围是 四、小结 小组交流,展示当堂测试归纳总结
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
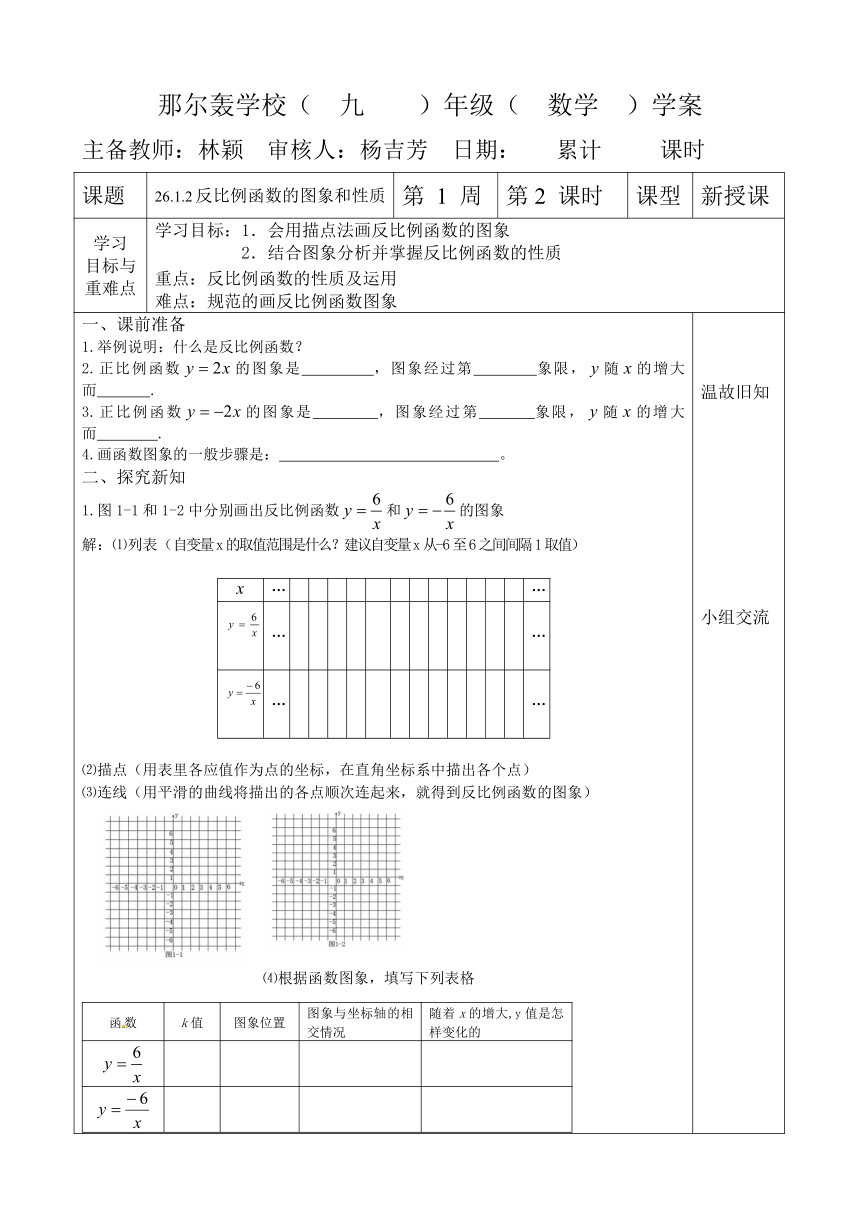
课题 26.1.2反比例函数的图象和性质 第 1 周 第2 课时 课型 新授课
学习目标与重难点 学习目标:1.会用描点法画反比例函数的图象2.结合图象分析并掌握反比例函数的性质重点:反比例函数的性质及运用难点:规范的画反比例函数图象
一、课前准备1.举例说明:什么是反比例函数?2.正比例函数的图象是 ,图象经过第 象限,随的增大而 .3.正比例函数的图象是 ,图象经过第 象限,随的增大而 .4.画函数图象的一般步骤是: 。二、探究新知………………1.图1-1和1-2中分别画出反比例函数和的图象解:⑴列表(自变量x的取值范围是什么?建议自变量x从-6至6之间间隔1取值)⑵描点(用表里各应值作为点的坐标,在直角坐标系中描出各个点)⑶连线(用平滑的曲线将描出的各点顺次连起来,就得到反比例函数的图象)函数k值图象位置图象与坐标轴的相交情况随着x的增大,y值是怎样变化的⑷根据函数图象,填写下列表格 温故旧知小组交流
归纳函数图象的性质:1.反比例函数的图象是 .2.反比例函数的性质:(可类比正比例函数的性质)(1)k>0 .(2)k<0 . 三、巩固提高(一)选择题1.已知反比例函数y= ,下列结论中,不正确的是( )A 图象经过点(1,2) B y随x的增大而减小C 图象在第一、三象限内 D y随x的减小而减小2.若反比例函数 的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )A.-1 B.3 C.0 D.-33.已知点A()、B()是反比例函数图象上的两点,则有()A. B.C. D.(二)填空题1.函数的图象是 .2.已知在一个反比例函数图象中,函数值随自变量值的增大而减小,请写出一个符合条件的函数解析式 .3.如图2,所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是 . (三)解答题(能力提高)已知:双曲线y=的图象经过A(1,2)、B(2,b)两点.(1)求双曲线的解析式;(2)试比较b与2的大小. 总结归纳练习巩固
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1.2反比例函数图象和性质2 第 1 周 第 3时 课型 新授课
学习目标与重难点 学习目标:1.认识反比例函数的图象与性质,并能简单运用. 2.利用反比例函数的图象性质,渗透数形结合的思想方法.学习重、难点:分析并掌握反比例函数的性质
一、课前准备反比例函数y =(k为常数,k≠0)的图象是 .当k>0时, ;当k<0时, .二、自主学习1.已知反比例函数y=的图象经过点A(2,—4).(1)求k的值; (2)这个函数的图象在哪几个象限?y随x的增大怎样变化?(3)画出函数的图象; (4)点B(,—16)、C(—3,5)在这个函数的图象上吗?2.已知反比例函数 y =的图象上有两点P(1,a), Q(b,2.5).(1) 求a、b的值;(2) 过点P作y轴的垂线交y轴于点M,求△PMO的面积;(3) 过点Q作x轴的垂线交x轴于点N,求△QNO的面积;(4)过双曲线上任意一点A(m,n)作x轴(或y轴)的垂线,垂足为B,求△ABO的面积;(5)你发现了什么规律? 温故旧知小组合作
三、巩固提高1、反比例函数①y=;②y=;③7y= —;④y=的图象中:(1)在第一、三象限的是 ,在第二、四象限的是 (2)在其所在的每一个象限内,y随x的增大而增大的是 2.已知反比例函数的图象经过点A(—6,—3).(1)写出函数关系式;(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?(3)点B(4,),C(2,—5)在这个函数的图象上吗?3.若反比例函数y=的图象经过第二、四象限,求函数的解析式。4.函数y=与y=ax的图象的一个交点A的坐标是(-1,-3),(1)求这两个函数的解析式;(2)在同一直角坐标系内,画出它们的图象;(3)你能求出这两个图象的另一个交点B的坐标吗?怎样求? 归纳总结
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1反比例函数 第 1 周 第4 课时 课型 练习课
学习目标与重难点 学习目标:1.认识反比例函数的图象与性质,并能简单运用. 2.利用反比例函数的图象性质,渗透数形结合的思想方法.学习重、难点:分析并掌握反比例函数的性质
习题检测1.已知反比例函数y=(k≠0)与一次函数y=x 的图象有交点, 则k 的范围是______ .2.已知反比例函数,当时,其图象的两个分支在第二、四象限内;当时,其图象在每个象限内随的增大而减小.3.若反比例函数的图象位于一、三象限内,正比例函数过二、四象限,则k的整数值是________.4.已知P(1,m+1)在双曲线上,则双曲线在第_________象限,在每个象限y随x的增大而________.5.若点(3,4)是反比例函数y= 图象上一点,则此函数图象必经过点( ) A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)6.一次函数y=kx-k 与反比例函数y=在同一直角坐标系内的图象大致( )7.下列函数中,当x>0时,y随x的增大而增大的是 ( )A.y=2-3x B.y= C.y=-2x-1 D.y=-8.已知一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数 的图象在( )A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限
9.函数y=-ax+a与(a≠0)在同一坐标系中的图象可能是( ) 10.下列函数中,图象大致为如图的是( )A.y= (x<0) B.y= (x>0) C.y=- (x>0) D.y=- (x<0)11.已知圆柱体的侧面积为80cm2,若圆柱底面半径为r(cm),高线长为h(cm),则h关于r的函数的图象大致是( )12.如图所示,一个反比例函数的图象在第二象限内,点A 是图象上的任意一点,AM⊥x轴于M,O是原点,若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.13.已知反比例函数图象与直线和的图象过同一点.(1)求反比例函数;(2)当>0时,这个反比例函数值随的增大如何变化?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1反比例函数2 第 1 周 第 5 课时 课型 复习课
学习目标与重难点 学习目标:1.认识反比例函数的图象与性质,并能简单运用. 2.利用反比例函数的图象性质,渗透数形结合的思想方法.学习重、难点:分析并掌握反比例函数的性质
一、填空题:1、函数和函数的图象有 个交点;2、反比例函数的图象经过(-,5)点、()及()点,则= ,= ,= ;3、若反比例函数的图象经过二、四象限,则=_______4、已知y-2与x成反比例,当x=3时,y =1,则与间的函数关系式为 ;5、已知正比例函数与反比例函数的图象都过A(,1),则= ,正比例函数的解析式是 ;6、设有反比例函数,、为其图象上的两点,若时,,则的取值范围是___________二、选择题7、下列函数中,是反比例函数的是( ) A. B. C. D. 8、 函数与()的图象的交点个数是( )A. 0 B. 1 C. 2 D. 不确定9、向高为H的圆柱形水杯中注水,已知水杯底面半径为2,那么注水量y与水深x的函数图象是( )
三、解下列各题10、已知函数,其中成正比例,成反比例,且当x=1时,y=1; 当x=3时,y=5.求当x=4时,y的值。11、如图,Rt△AOB顶点A是一次函数的图象与反比例函数的 图象在第二象限内的交点,且S△AOB=1,求一次函数解析式. 12.如图,一次函数的图象与反比例函数的图象相交于A、B两点,(1)利用图中条件,求反比例函数和一次函数的解析式(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 17.2实际问题与反比例函数 第2 周 第 1 课时 课型 新授课
学习目标与重难点 学习目标:1、学会把实际问题转化为数学问题,进一步理解反比例函数关系式的构造,掌握用反比例函数的方法解决实际问题.2、经历“实际问题——建立模型——拓展应用”的过程发展学生分析问题,解决问题的能力。重点:用反比例函数解决实际问题难点:构建反比例函数的数学模型
课前准备1、反比例函数的定义: 2、反比例函数的一般式: 探究新知公元前3世纪,古希腊科学家阿基米德发现了著名的“杠杆定律”:若两物体与支点的距离反比于其重量,则杠杆平衡.也可这样描述:阻力×阻力臂=动力×动力臂. 为此,他留下一句名言:给我一个支点,我可以撬动地球!问题:小伟想用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别是1200N和0.5m.(1)动力F和动力臂L有怎样的函数关系?(2)当动力臂为1.5m时,撬动石头至少要多大的力? 新知应用:例题二:在某一电路中,电源电压U保持不变,电流I(A)与电阻R(Ω)之间的函数关系如图所示.(1)写出I与R之间的函数解析式;(2)结合图象回答:当电路中的电流不超过2A时,电路中电阻R的取值范围是什么?例题三、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气球体积V(m3)的反比例函数,其图象如图所示(千帕是一种压强单位). (1)写出这个函数的解析式; (2)当气球体积为0.8m3时,气球内的气压是多少千帕?(3)当气球内的气压大于144千帕时,气球将爆炸,为了完全起见,气球的体积应不小于多少?
巩固提高1.在一定的范围内,某种物品的需求量与供应量成反比例.现已知当需求量为500吨时,市场供应量为10 000吨,试求当市场供应量为16000吨时的需求量是 .2.某电厂有5 000吨电煤. (1)这些电煤能够使用的天数x(天)与该厂平均每天用煤吨数y(吨)之间的函数关系是 ; (2)若平均每天用煤200吨,这批电煤能用 天; (3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用煤300吨,这批电煤共可用 天.3.一种电器的使用寿命n(月)与平均每天使用时间t(小时)成反比例,其关系如图所示. (1)求使用寿命n(月)与平均每天使用时间t(小时)之间的函数关系式是 ;(2)当t=5小时,电器的使用寿命 . 4.某人用50N的恒定压力用气筒给车胎打气. (1)打气所产生的压强P(帕)与受力面积S(米2)之间的函数关系是: . (2)若受力面积是100cm2,则产生的压强是 ; (3)你能根据这一知识解释:为什么刀刃越锋利,刀具就越好用吗?为什么坦克的轮子上安装又宽又长的履带呢?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.2实际问题与反比例函数2 第2 周 第2 课时 课型 新授课
学习目标与重难点 学习目标:1、反比例函数知识解决一些实际问题。 2、体会数学与物理间的密切联系,增强应用意识,提高运用代数方法解决问题的能力。重点:掌握从物理力学、电学问题中建构反比列函数的模型。难点:从实际问题中寻找变量之间的关系,关键还是充分运用所学的知识分析物理问题,建立函数模型,教学时注意分析过程,渗透数形结合的思想。
一、课前准备用电器的输出功率P(瓦)、两端的电压U(伏)及用电器的电阻R(欧姆)有如下关系:PR=U2这个关系也可写为P=_______,或R=________。二、探究新知1.一个用电器的电阻是可调节的,其范围为110~220欧姆。已知电压为220伏,这个用电器的电路图如图1所示。输出功率P与电阻R有怎样的函数关系?这个用电器输出功率的范围多大?2.为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范为 ;药物燃烧后,y关于x的函数关系式为 .(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过______分钟后,员工才能回到办公室;(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效 为什么
三、巩固提高1.某厂现有800吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )(A)(x>0) (B)(x≥0)(C)y=300x(x≥0) (D)y=300x(x>0)2.已知甲、乙两地相s(千米),汽车从甲地匀速行驶到达乙地,如果汽车每小时耗油量为a(升),那么从甲地到乙地汽车的总耗油量y(升)与汽车的行驶速度v(千米/时)的函数图象大致是( ) 3.在一个可改变容积的密闭容器内,装有一定质量的某种气体,当改变容积时,气体的密度ρ也随之改变。ρ与在一定范围内满足ρ,它的图象如图所示,则该气体质量为( )。 A. B. C. D. 7.4.你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识,一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示:(1)写出y与S的函数关系式;(2)求当面条粗1.6mm2时,面条的总长度是多少米?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26反比例函数的应用1 第 2 周 第 3 课时 课型 新授课
学习目标与重难点 学习目标:1.能灵活运用反比例函数的知识解决实际问题.2.经历“实际问题-建立模型-拓展应用”的过程,培养分析和解决问题的能力.重、难点:把实际问题转化为反比例函数这一数学模型,渗透转化的数学思想.
课前准备1、反比例函数是刻画现实问题中数量关系的一种数学模型,它与一次函数、正比例函数一样,在生活、生产实际中也有着广泛的应用。2、在一个实际问题中,两个变量x、y满足关系式 (k为常数,k≠0),则y就是x的反比例函数.这时,若给出x的某一数值,则可求出对应的y值,反之亦然。二、探究新知例1.小明将一篇24000字的社会调查报告录入电脑,打印成文.⑴如果小明以每分钟120字的速度录入,他需要多长时间才能完成录入任务?⑵完成录入的时间t(min)与录入文字的速度V(字/min)有怎样的函数关系?⑶小明希望能在3h内完成录入任务,那么他每分钟至少应录入多少个字?例2.某自来水公司计划新建一个容积为4×104m3的长方体蓄水池.⑴蓄水池的底面积S(m2)与其深度h(m)有怎样的函数关系?⑵如果蓄水池的深度设计为5m,那么蓄水池的底面积应为多少平方米?⑶由于绿化以及辅助用地的需要,经过实地测量,蓄水池的长和宽最多能分别设计为100m和60m,那么蓄水池的深度至少达到多少才能满足要求?(保留两位小数)小结:1.例1中当录入文字总量一定时,则录入时间是录入速度的反比例函数;例2中当____________一定时,则________是________的反比例函数。生活中还有许多反比例函数模型的实际问题,你能举出例子吗? 2.在实际问题中,反比例函数 (k为常数,k≠0)的自变量x、因变量y的取值一般为____数或______整数。当其中一个变量取最大值(最多、不超过)时,相应的另一变量必然是取_______ ( ___________ )。
三、巩固练习1.某蓄水池的排水管每小时排水8m3 ,6h可将满池水全部排空. (1)蓄水池的容积是多少? (2)如果增加排水管,使每小时排水量达到Q(m3),那么将满池水排空所需时间t(h)将如何变化?写出t与Q之间关系式(3)如果准备在5小时内将满池水排空,那么每小时的排水量至少是多少? (4)已知排水管每小时最多排水12 m3,则至少需几小时可将满池水全部排空?2.如图,矩形ABCD中,AB=6,AD=8,点P在BC边上移动(不与点B、C重合),设PA=x,点D到PA的距离DE=y.求y与x之间的函数关系式及自变量x的取值范围.3.为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:⑴药物燃烧时y关于x的函数关系式为 ,自变量的取值范围是 ;⑵药物燃烧后y与x的函数关系式为 ,自变量的取值范围是 ;⑶研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室;⑷研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26章反比例函数的应用2 第 2周 第 4课时 课型 新授课
学习目标与重难点 学习目标:1.待定系数法求反比例函数的关系式;2.根据所给反比例函数与一次函数的图象解决综合问题。重、难点:根据所给反比例函数与一次函数的图象解决综合问题,感受数形结合的思想方法
一、知识回顾1.什么是反比例函数?____________________(写出一般式) (变式)2.其图像是_____线3.它有什么性质?(画出草图回答) ⑴ 增减性:当k>0时, ⑵当k<0时, ⑶中心对称性:若(a,b)是分支上一点,则它关于原点的对称点(_____)必在另一分支上.二、课前预热1.已知反比例函数的图象经过点(1,2),则k的值是___________________.2.已知反比例函数,其图象在第一、三象限内,则k的取值范围是__________.3.若双曲线经过点A(m,-2m),则m的值为____________.4.双曲线和一次函数的图象的两个交点分别是A(-1,-4),B(2,m),则a+2b=_________________.5.在电压一定的情况下,电流I(单位:安培)与电阻R(单位:欧姆)之间满足如图所示的反比例函数关系,则I关于R的函数表达式为______________________.三、合作探究1.已知反比例函数经过点A(2,-m)和点B(n,2n),求:(1)m和n的值; (2)画出它的草图;(3)若图象上有两点P1(x1,y1)和P2(x2,y2),且x1<0<x2,试比较y1和y2的大小.
2.若反比例函数的图像在所在象限内,y随x的增大而增大,求n的值.3.如图,已知一次函数的图象与x轴,y轴分别交于A、B两点,且与反比例函数的图象在第一象限内交于点C,CD⊥x轴,垂足为D,若OA=OB=OD=1.(1)求点A、B的坐标;(2)求一次函数和反比例函数的解析式. (3)写出在第一象限内,一次函数的值小于反比例函数的值x的取值范围.4.如图,一次函数的图象与x轴,y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、第三象限,且OA=OB=AC=BD.求一次函数和反比例函数的解析式.
课后反思
图2
输入x
取倒数
×(-5)
输出y
1
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1.1反比例函数的意义 第 1 周 第 1 课时 课型 新授课
学习目标与重难点 学习目标:1、理解并掌握反比例函数的概念。2、能判断一个给定的函数是否为反比例函数,并会用待定系数法求函数解析式。学习重点:理解反比例函数的概念,能根据已知条件写出函数解析式学习难点:理解反比例函数的概念。
课前准备回忆一下什么是正比例函数、一次函数?它们的一般形式是怎样的?探究新知问题提出:电流I、电阻R、电压U之间满足关系式U=IR,当U=220V时,(1)你能用含有R的代数式表示I吗?(2)利用写出的关系式完成下表:R/Ω20406080100I/A当R越来越大时,I怎样变化?当R越来越小呢?(3)变量I是R的函数吗?为什么?学生小组合作讨论。概念:如果两个变量x,y之间的关系可以表示成 的形式,那么y是x的 函数,反比例函数的自变量x有什么条件?新知应用1.下列问题中,变量间的对应关系可用怎样的函数关系式表示?这些函数有什么共同特点?(1)京沪线铁路全程为1463km,乘坐某次列车所用时间t(单位:h)随该列车平均速度v(单位:km/h)的变化而变化;_________________(2)某住宅小区要种植一个面积为1000m2的矩形草坪,草坪的长为y随宽x的变化;_________________(3)已知北京市的总面积为1.68×104平方千米,人均占有的土地面积S(平方千米/人)随全市总人口数n(单位:人)的变化而变化。_________________上面的函数关系式,都具有_____________的形式,其中_________是常数。 学生回忆旧知小组合作,探究反比例函数变量的相依关系,领会其概念。
2.一个矩形的面积为20,相邻的两条边长分别为xcm和ycm。那么变量y是变量x的函数吗?为什么?3.y是x的反比例函数,下表给出了x与y的一些值:x-2-113…y2-1……(1)写出这个反比例函数的表达式;(2)根据函数表达式完成上表。三、当堂检测:1.下列等式中,哪些是反比例函数(1) (2) (3)xy=21 (4) (5)(6) (7)y=x-42.当m取什么值时,函数是反比例函数?3.苹果每千克x元,花10元钱可买y千克的苹果,则y与x之间的函数关系式为 4.若函数是反比例函数,则m的取值是 5.矩形的面积为4,一条边的长为x,另一条边的长为y,则y与x的函数解析式为 6.已知y与x成反比例,且当x=-2时,y=3,则y与x之间的函数关系式是 ,当x=-3时,y= 7.函数中自变量x的取值范围是 四、小结 小组交流,展示当堂测试归纳总结
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1.2反比例函数的图象和性质 第 1 周 第2 课时 课型 新授课
学习目标与重难点 学习目标:1.会用描点法画反比例函数的图象2.结合图象分析并掌握反比例函数的性质重点:反比例函数的性质及运用难点:规范的画反比例函数图象
一、课前准备1.举例说明:什么是反比例函数?2.正比例函数的图象是 ,图象经过第 象限,随的增大而 .3.正比例函数的图象是 ,图象经过第 象限,随的增大而 .4.画函数图象的一般步骤是: 。二、探究新知………………1.图1-1和1-2中分别画出反比例函数和的图象解:⑴列表(自变量x的取值范围是什么?建议自变量x从-6至6之间间隔1取值)⑵描点(用表里各应值作为点的坐标,在直角坐标系中描出各个点)⑶连线(用平滑的曲线将描出的各点顺次连起来,就得到反比例函数的图象)函数k值图象位置图象与坐标轴的相交情况随着x的增大,y值是怎样变化的⑷根据函数图象,填写下列表格 温故旧知小组交流
归纳函数图象的性质:1.反比例函数的图象是 .2.反比例函数的性质:(可类比正比例函数的性质)(1)k>0 .(2)k<0 . 三、巩固提高(一)选择题1.已知反比例函数y= ,下列结论中,不正确的是( )A 图象经过点(1,2) B y随x的增大而减小C 图象在第一、三象限内 D y随x的减小而减小2.若反比例函数 的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )A.-1 B.3 C.0 D.-33.已知点A()、B()是反比例函数图象上的两点,则有()A. B.C. D.(二)填空题1.函数的图象是 .2.已知在一个反比例函数图象中,函数值随自变量值的增大而减小,请写出一个符合条件的函数解析式 .3.如图2,所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是 . (三)解答题(能力提高)已知:双曲线y=的图象经过A(1,2)、B(2,b)两点.(1)求双曲线的解析式;(2)试比较b与2的大小. 总结归纳练习巩固
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1.2反比例函数图象和性质2 第 1 周 第 3时 课型 新授课
学习目标与重难点 学习目标:1.认识反比例函数的图象与性质,并能简单运用. 2.利用反比例函数的图象性质,渗透数形结合的思想方法.学习重、难点:分析并掌握反比例函数的性质
一、课前准备反比例函数y =(k为常数,k≠0)的图象是 .当k>0时, ;当k<0时, .二、自主学习1.已知反比例函数y=的图象经过点A(2,—4).(1)求k的值; (2)这个函数的图象在哪几个象限?y随x的增大怎样变化?(3)画出函数的图象; (4)点B(,—16)、C(—3,5)在这个函数的图象上吗?2.已知反比例函数 y =的图象上有两点P(1,a), Q(b,2.5).(1) 求a、b的值;(2) 过点P作y轴的垂线交y轴于点M,求△PMO的面积;(3) 过点Q作x轴的垂线交x轴于点N,求△QNO的面积;(4)过双曲线上任意一点A(m,n)作x轴(或y轴)的垂线,垂足为B,求△ABO的面积;(5)你发现了什么规律? 温故旧知小组合作
三、巩固提高1、反比例函数①y=;②y=;③7y= —;④y=的图象中:(1)在第一、三象限的是 ,在第二、四象限的是 (2)在其所在的每一个象限内,y随x的增大而增大的是 2.已知反比例函数的图象经过点A(—6,—3).(1)写出函数关系式;(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?(3)点B(4,),C(2,—5)在这个函数的图象上吗?3.若反比例函数y=的图象经过第二、四象限,求函数的解析式。4.函数y=与y=ax的图象的一个交点A的坐标是(-1,-3),(1)求这两个函数的解析式;(2)在同一直角坐标系内,画出它们的图象;(3)你能求出这两个图象的另一个交点B的坐标吗?怎样求? 归纳总结
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1反比例函数 第 1 周 第4 课时 课型 练习课
学习目标与重难点 学习目标:1.认识反比例函数的图象与性质,并能简单运用. 2.利用反比例函数的图象性质,渗透数形结合的思想方法.学习重、难点:分析并掌握反比例函数的性质
习题检测1.已知反比例函数y=(k≠0)与一次函数y=x 的图象有交点, 则k 的范围是______ .2.已知反比例函数,当时,其图象的两个分支在第二、四象限内;当时,其图象在每个象限内随的增大而减小.3.若反比例函数的图象位于一、三象限内,正比例函数过二、四象限,则k的整数值是________.4.已知P(1,m+1)在双曲线上,则双曲线在第_________象限,在每个象限y随x的增大而________.5.若点(3,4)是反比例函数y= 图象上一点,则此函数图象必经过点( ) A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)6.一次函数y=kx-k 与反比例函数y=在同一直角坐标系内的图象大致( )7.下列函数中,当x>0时,y随x的增大而增大的是 ( )A.y=2-3x B.y= C.y=-2x-1 D.y=-8.已知一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数 的图象在( )A.第一、二象限 B.第三、四象限 C.第一、三象限 D.第二、四象限
9.函数y=-ax+a与(a≠0)在同一坐标系中的图象可能是( ) 10.下列函数中,图象大致为如图的是( )A.y= (x<0) B.y= (x>0) C.y=- (x>0) D.y=- (x<0)11.已知圆柱体的侧面积为80cm2,若圆柱底面半径为r(cm),高线长为h(cm),则h关于r的函数的图象大致是( )12.如图所示,一个反比例函数的图象在第二象限内,点A 是图象上的任意一点,AM⊥x轴于M,O是原点,若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.13.已知反比例函数图象与直线和的图象过同一点.(1)求反比例函数;(2)当>0时,这个反比例函数值随的增大如何变化?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.1反比例函数2 第 1 周 第 5 课时 课型 复习课
学习目标与重难点 学习目标:1.认识反比例函数的图象与性质,并能简单运用. 2.利用反比例函数的图象性质,渗透数形结合的思想方法.学习重、难点:分析并掌握反比例函数的性质
一、填空题:1、函数和函数的图象有 个交点;2、反比例函数的图象经过(-,5)点、()及()点,则= ,= ,= ;3、若反比例函数的图象经过二、四象限,则=_______4、已知y-2与x成反比例,当x=3时,y =1,则与间的函数关系式为 ;5、已知正比例函数与反比例函数的图象都过A(,1),则= ,正比例函数的解析式是 ;6、设有反比例函数,、为其图象上的两点,若时,,则的取值范围是___________二、选择题7、下列函数中,是反比例函数的是( ) A. B. C. D. 8、 函数与()的图象的交点个数是( )A. 0 B. 1 C. 2 D. 不确定9、向高为H的圆柱形水杯中注水,已知水杯底面半径为2,那么注水量y与水深x的函数图象是( )
三、解下列各题10、已知函数,其中成正比例,成反比例,且当x=1时,y=1; 当x=3时,y=5.求当x=4时,y的值。11、如图,Rt△AOB顶点A是一次函数的图象与反比例函数的 图象在第二象限内的交点,且S△AOB=1,求一次函数解析式. 12.如图,一次函数的图象与反比例函数的图象相交于A、B两点,(1)利用图中条件,求反比例函数和一次函数的解析式(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 17.2实际问题与反比例函数 第2 周 第 1 课时 课型 新授课
学习目标与重难点 学习目标:1、学会把实际问题转化为数学问题,进一步理解反比例函数关系式的构造,掌握用反比例函数的方法解决实际问题.2、经历“实际问题——建立模型——拓展应用”的过程发展学生分析问题,解决问题的能力。重点:用反比例函数解决实际问题难点:构建反比例函数的数学模型
课前准备1、反比例函数的定义: 2、反比例函数的一般式: 探究新知公元前3世纪,古希腊科学家阿基米德发现了著名的“杠杆定律”:若两物体与支点的距离反比于其重量,则杠杆平衡.也可这样描述:阻力×阻力臂=动力×动力臂. 为此,他留下一句名言:给我一个支点,我可以撬动地球!问题:小伟想用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别是1200N和0.5m.(1)动力F和动力臂L有怎样的函数关系?(2)当动力臂为1.5m时,撬动石头至少要多大的力? 新知应用:例题二:在某一电路中,电源电压U保持不变,电流I(A)与电阻R(Ω)之间的函数关系如图所示.(1)写出I与R之间的函数解析式;(2)结合图象回答:当电路中的电流不超过2A时,电路中电阻R的取值范围是什么?例题三、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(千帕)是气球体积V(m3)的反比例函数,其图象如图所示(千帕是一种压强单位). (1)写出这个函数的解析式; (2)当气球体积为0.8m3时,气球内的气压是多少千帕?(3)当气球内的气压大于144千帕时,气球将爆炸,为了完全起见,气球的体积应不小于多少?
巩固提高1.在一定的范围内,某种物品的需求量与供应量成反比例.现已知当需求量为500吨时,市场供应量为10 000吨,试求当市场供应量为16000吨时的需求量是 .2.某电厂有5 000吨电煤. (1)这些电煤能够使用的天数x(天)与该厂平均每天用煤吨数y(吨)之间的函数关系是 ; (2)若平均每天用煤200吨,这批电煤能用 天; (3)若该电厂前10天每天用200吨,后因各地用电紧张,每天用煤300吨,这批电煤共可用 天.3.一种电器的使用寿命n(月)与平均每天使用时间t(小时)成反比例,其关系如图所示. (1)求使用寿命n(月)与平均每天使用时间t(小时)之间的函数关系式是 ;(2)当t=5小时,电器的使用寿命 . 4.某人用50N的恒定压力用气筒给车胎打气. (1)打气所产生的压强P(帕)与受力面积S(米2)之间的函数关系是: . (2)若受力面积是100cm2,则产生的压强是 ; (3)你能根据这一知识解释:为什么刀刃越锋利,刀具就越好用吗?为什么坦克的轮子上安装又宽又长的履带呢?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26.2实际问题与反比例函数2 第2 周 第2 课时 课型 新授课
学习目标与重难点 学习目标:1、反比例函数知识解决一些实际问题。 2、体会数学与物理间的密切联系,增强应用意识,提高运用代数方法解决问题的能力。重点:掌握从物理力学、电学问题中建构反比列函数的模型。难点:从实际问题中寻找变量之间的关系,关键还是充分运用所学的知识分析物理问题,建立函数模型,教学时注意分析过程,渗透数形结合的思想。
一、课前准备用电器的输出功率P(瓦)、两端的电压U(伏)及用电器的电阻R(欧姆)有如下关系:PR=U2这个关系也可写为P=_______,或R=________。二、探究新知1.一个用电器的电阻是可调节的,其范围为110~220欧姆。已知电压为220伏,这个用电器的电路图如图1所示。输出功率P与电阻R有怎样的函数关系?这个用电器输出功率的范围多大?2.为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范为 ;药物燃烧后,y关于x的函数关系式为 .(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过______分钟后,员工才能回到办公室;(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效 为什么
三、巩固提高1.某厂现有800吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )(A)(x>0) (B)(x≥0)(C)y=300x(x≥0) (D)y=300x(x>0)2.已知甲、乙两地相s(千米),汽车从甲地匀速行驶到达乙地,如果汽车每小时耗油量为a(升),那么从甲地到乙地汽车的总耗油量y(升)与汽车的行驶速度v(千米/时)的函数图象大致是( ) 3.在一个可改变容积的密闭容器内,装有一定质量的某种气体,当改变容积时,气体的密度ρ也随之改变。ρ与在一定范围内满足ρ,它的图象如图所示,则该气体质量为( )。 A. B. C. D. 7.4.你吃过拉面吗?实际上在做拉面的过程中就渗透着数学知识,一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示:(1)写出y与S的函数关系式;(2)求当面条粗1.6mm2时,面条的总长度是多少米?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26反比例函数的应用1 第 2 周 第 3 课时 课型 新授课
学习目标与重难点 学习目标:1.能灵活运用反比例函数的知识解决实际问题.2.经历“实际问题-建立模型-拓展应用”的过程,培养分析和解决问题的能力.重、难点:把实际问题转化为反比例函数这一数学模型,渗透转化的数学思想.
课前准备1、反比例函数是刻画现实问题中数量关系的一种数学模型,它与一次函数、正比例函数一样,在生活、生产实际中也有着广泛的应用。2、在一个实际问题中,两个变量x、y满足关系式 (k为常数,k≠0),则y就是x的反比例函数.这时,若给出x的某一数值,则可求出对应的y值,反之亦然。二、探究新知例1.小明将一篇24000字的社会调查报告录入电脑,打印成文.⑴如果小明以每分钟120字的速度录入,他需要多长时间才能完成录入任务?⑵完成录入的时间t(min)与录入文字的速度V(字/min)有怎样的函数关系?⑶小明希望能在3h内完成录入任务,那么他每分钟至少应录入多少个字?例2.某自来水公司计划新建一个容积为4×104m3的长方体蓄水池.⑴蓄水池的底面积S(m2)与其深度h(m)有怎样的函数关系?⑵如果蓄水池的深度设计为5m,那么蓄水池的底面积应为多少平方米?⑶由于绿化以及辅助用地的需要,经过实地测量,蓄水池的长和宽最多能分别设计为100m和60m,那么蓄水池的深度至少达到多少才能满足要求?(保留两位小数)小结:1.例1中当录入文字总量一定时,则录入时间是录入速度的反比例函数;例2中当____________一定时,则________是________的反比例函数。生活中还有许多反比例函数模型的实际问题,你能举出例子吗? 2.在实际问题中,反比例函数 (k为常数,k≠0)的自变量x、因变量y的取值一般为____数或______整数。当其中一个变量取最大值(最多、不超过)时,相应的另一变量必然是取_______ ( ___________ )。
三、巩固练习1.某蓄水池的排水管每小时排水8m3 ,6h可将满池水全部排空. (1)蓄水池的容积是多少? (2)如果增加排水管,使每小时排水量达到Q(m3),那么将满池水排空所需时间t(h)将如何变化?写出t与Q之间关系式(3)如果准备在5小时内将满池水排空,那么每小时的排水量至少是多少? (4)已知排水管每小时最多排水12 m3,则至少需几小时可将满池水全部排空?2.如图,矩形ABCD中,AB=6,AD=8,点P在BC边上移动(不与点B、C重合),设PA=x,点D到PA的距离DE=y.求y与x之间的函数关系式及自变量x的取值范围.3.为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:⑴药物燃烧时y关于x的函数关系式为 ,自变量的取值范围是 ;⑵药物燃烧后y与x的函数关系式为 ,自变量的取值范围是 ;⑶研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室;⑷研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
课后反思
那尔轰学校( 九 )年级( 数学 )学案
主备教师:林颖 审核人:杨吉芳 日期: 累计 课时
课题 26章反比例函数的应用2 第 2周 第 4课时 课型 新授课
学习目标与重难点 学习目标:1.待定系数法求反比例函数的关系式;2.根据所给反比例函数与一次函数的图象解决综合问题。重、难点:根据所给反比例函数与一次函数的图象解决综合问题,感受数形结合的思想方法
一、知识回顾1.什么是反比例函数?____________________(写出一般式) (变式)2.其图像是_____线3.它有什么性质?(画出草图回答) ⑴ 增减性:当k>0时, ⑵当k<0时, ⑶中心对称性:若(a,b)是分支上一点,则它关于原点的对称点(_____)必在另一分支上.二、课前预热1.已知反比例函数的图象经过点(1,2),则k的值是___________________.2.已知反比例函数,其图象在第一、三象限内,则k的取值范围是__________.3.若双曲线经过点A(m,-2m),则m的值为____________.4.双曲线和一次函数的图象的两个交点分别是A(-1,-4),B(2,m),则a+2b=_________________.5.在电压一定的情况下,电流I(单位:安培)与电阻R(单位:欧姆)之间满足如图所示的反比例函数关系,则I关于R的函数表达式为______________________.三、合作探究1.已知反比例函数经过点A(2,-m)和点B(n,2n),求:(1)m和n的值; (2)画出它的草图;(3)若图象上有两点P1(x1,y1)和P2(x2,y2),且x1<0<x2,试比较y1和y2的大小.
2.若反比例函数的图像在所在象限内,y随x的增大而增大,求n的值.3.如图,已知一次函数的图象与x轴,y轴分别交于A、B两点,且与反比例函数的图象在第一象限内交于点C,CD⊥x轴,垂足为D,若OA=OB=OD=1.(1)求点A、B的坐标;(2)求一次函数和反比例函数的解析式. (3)写出在第一象限内,一次函数的值小于反比例函数的值x的取值范围.4.如图,一次函数的图象与x轴,y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,如果A点的坐标为(2,0),点C、D分别在第一、第三象限,且OA=OB=AC=BD.求一次函数和反比例函数的解析式.
课后反思
图2
输入x
取倒数
×(-5)
输出y
1
