18.2.3.正方形课件
图片预览




文档简介
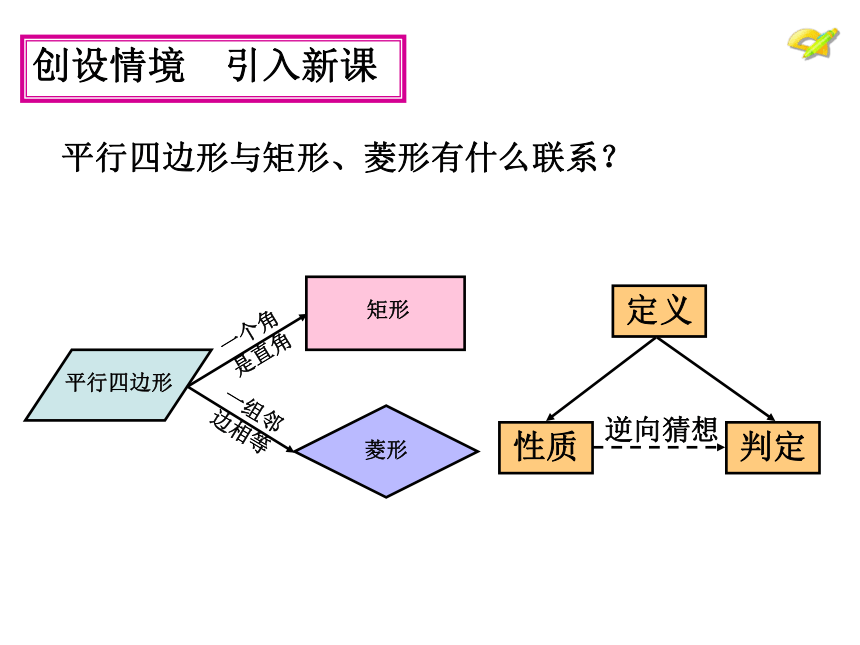
课件27张PPT。创设情境 引入新课 平行四边形与矩形、菱形有什么联系?一个角
是直角 一组邻
边相等 创设情境 引入新知 除了矩形和菱形外,还有什么特殊的平行四边形吗? 怎样研究这类图形?
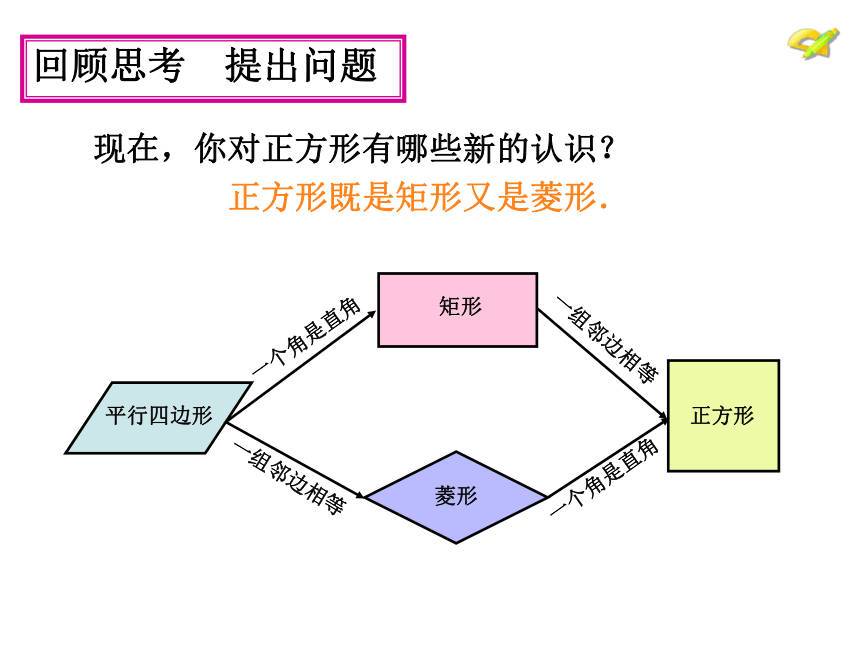
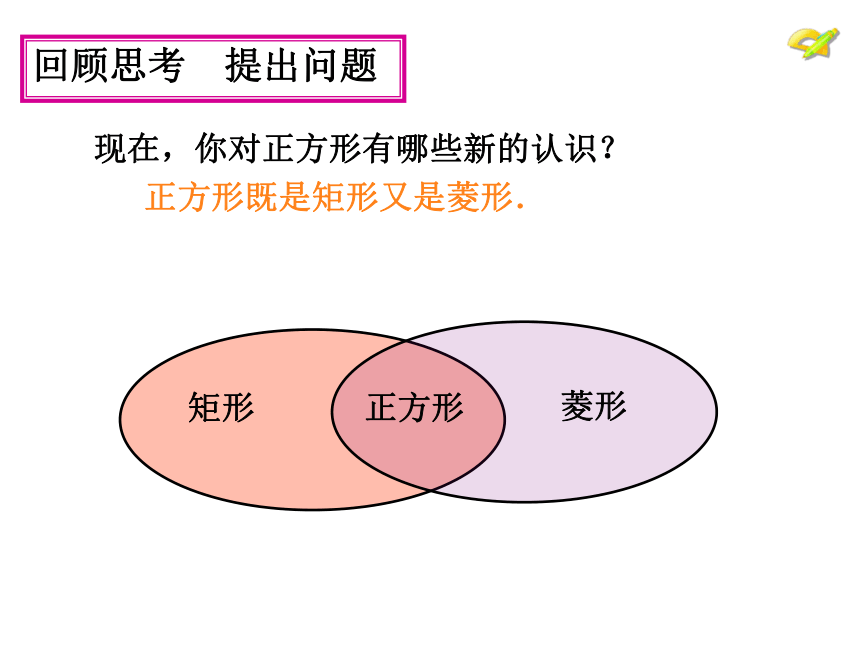
先看看我们是怎样研究矩形和菱形的.回顾思考 提出问题 现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形. 一个角是直角 一组邻边相等 一组邻边相等 一个角是直角 回顾思考 提出问题 现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形. 二、探究新知1.正方形的概念:做一做:
用一张长方形的纸片折出一个正方形. 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.三个条件一组邻边相等一个角是直角平行四边形2.正方形的性质: 正方形是特殊的平行四边形,也是特殊的矩形、菱形.所以它具有这些图形的所有性质.四条边相等四个角是直角对角线相等并且互相垂直平分,每一条对角线平分一组对角.正方形是轴对称图形,有四条对称轴.三、应用新知 例1 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.证明:∵四边形ABCD是正方形, ∴AC=BD, AC⊥BD, AO=CO=BO=DO, ∴△ABO、△BCO、△CDO、△DAO
都是等腰直角三角形, 并且 △ABO ≌△BCO≌△CDO≌△DAO.
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图). 求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形. 复习:正方形的性质边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角正方形性质正方形具有平行四边形、矩形、菱 形的一切性质。1.如图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE,CE,
则∠DEC=( ) 30o2.如图,已知正方形ABCD内有一个△BEF,AB=6,
AF︰FD=1︰2,
E为DC的中点,
求△BEF的面积。D3、如图,点E是正方形ABCD边BC上延长线上一点,且CE=AC,若AE交CD于点F,求∠E和∠AFC的度数。4、在正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于点E,PF⊥BD于点F,求PE+PF的值。三、应用新知 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE. xk 证明:在正方形ABDE中, AE=AB,∠EAB=90°, 又在正方形ACFG中, AG=AC,∠GAC=90°, ∴∠EAB=∠GAC=90°. ∴∠EAC=∠GAB, ∴△EAC≌△GAB,
∴EC=GB. ∵∠EAC=∠EAB+∠BAC, ∠GAB=∠GAC+∠BAC, 例2 如图,顺次连接正方形ABCD各边的中点,得
到四边形EFGH.求证:四边形EFGH也是正方形. 变式 如图,E,F,G,H分别是各边上的点,且
AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?变式训练有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角正方形、矩形、菱形及平行四边形四者之间的关系判断四边形是正方形有哪些方法?2、先说明它是矩形,再说明这个矩形有一组邻边相等.3、先说明它是菱形,再说明这个菱形有一个角是直角.1、先说明它是平行四边形,再说明有一组邻边相等,有一个角是直角。(定义法) 你觉得什么样的四边形是正方形呢?( 判断一个四边形是正方形有哪些方法?)正方形的判定方法:(可从平行四边形、矩形、菱形为基础)定义法①四条边相等,四个角都是直角②对角线互相垂直、平分且相等以四边形为基础:既是菱形又是矩形的四边形是正方形。5种识
别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等平行四边形、矩形、菱形、正方形的判定小结一展身手1、在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BCC ①、对角线相等的菱形是正方形 ②、对角线互相垂直的矩形是正方形③、对角线互相垂直且相等的四边
形是正方形④ 四条边都相等的四边形是正方形⑤、四个角都相等的四边形是正方形⑥、四边相等,有一个角是直角的四
边形是正方形. ( )( )( )( )( )( )判断下列命题哪些是真命题、哪些是假命题? 真真假假假真例3、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB。求证:四边形CEDF是正方形。∴四边形ABCD是正方形( )∴ DE=DF( )DE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形( )而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥BC有三个角是直角的四边形是矩形角平分线的定理有一组邻边相等的矩形是正方形7.如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D。DE⊥AC,DF⊥AB。求证:四边形CEDF为正方形ABCDEFG证明:过点D作DG⊥AB,垂足为G
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB
∴ DE=DG
同理:DG=DF
∴ED=DF
∵ DE⊥AC,DF⊥AB
∴∠DEC= ∠DFC=90 °
又∵ ∠C=90 °
∴四边形ADFC是矩形
∴四边形ADFC是正方形谢谢合作!
是直角 一组邻
边相等 创设情境 引入新知 除了矩形和菱形外,还有什么特殊的平行四边形吗? 怎样研究这类图形?
先看看我们是怎样研究矩形和菱形的.回顾思考 提出问题 现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形. 一个角是直角 一组邻边相等 一组邻边相等 一个角是直角 回顾思考 提出问题 现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形. 二、探究新知1.正方形的概念:做一做:
用一张长方形的纸片折出一个正方形. 有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.三个条件一组邻边相等一个角是直角平行四边形2.正方形的性质: 正方形是特殊的平行四边形,也是特殊的矩形、菱形.所以它具有这些图形的所有性质.四条边相等四个角是直角对角线相等并且互相垂直平分,每一条对角线平分一组对角.正方形是轴对称图形,有四条对称轴.三、应用新知 例1 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.证明:∵四边形ABCD是正方形, ∴AC=BD, AC⊥BD, AO=CO=BO=DO, ∴△ABO、△BCO、△CDO、△DAO
都是等腰直角三角形, 并且 △ABO ≌△BCO≌△CDO≌△DAO.
已知:四边形ABCD是正方形,对角线AC、BD相交于点O(如图). 求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形. 复习:正方形的性质边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角正方形性质正方形具有平行四边形、矩形、菱 形的一切性质。1.如图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE,CE,
则∠DEC=( ) 30o2.如图,已知正方形ABCD内有一个△BEF,AB=6,
AF︰FD=1︰2,
E为DC的中点,
求△BEF的面积。D3、如图,点E是正方形ABCD边BC上延长线上一点,且CE=AC,若AE交CD于点F,求∠E和∠AFC的度数。4、在正方形ABCD中,AC=10,P是AB上任意一点,PE⊥AC于点E,PF⊥BD于点F,求PE+PF的值。三、应用新知 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE. xk 证明:在正方形ABDE中, AE=AB,∠EAB=90°, 又在正方形ACFG中, AG=AC,∠GAC=90°, ∴∠EAB=∠GAC=90°. ∴∠EAC=∠GAB, ∴△EAC≌△GAB,
∴EC=GB. ∵∠EAC=∠EAB+∠BAC, ∠GAB=∠GAC+∠BAC, 例2 如图,顺次连接正方形ABCD各边的中点,得
到四边形EFGH.求证:四边形EFGH也是正方形. 变式 如图,E,F,G,H分别是各边上的点,且
AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?变式训练有一个角是直角有一组邻边相等有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角正方形、矩形、菱形及平行四边形四者之间的关系判断四边形是正方形有哪些方法?2、先说明它是矩形,再说明这个矩形有一组邻边相等.3、先说明它是菱形,再说明这个菱形有一个角是直角.1、先说明它是平行四边形,再说明有一组邻边相等,有一个角是直角。(定义法) 你觉得什么样的四边形是正方形呢?( 判断一个四边形是正方形有哪些方法?)正方形的判定方法:(可从平行四边形、矩形、菱形为基础)定义法①四条边相等,四个角都是直角②对角线互相垂直、平分且相等以四边形为基础:既是菱形又是矩形的四边形是正方形。5种识
别方法三个角是直角四条边相等一个角是直角或对角线相等一组邻边相等或对角线垂直一组邻边相等或对角线垂直一个角是直角或对角线相等一个角是直角且一组邻边相等平行四边形、矩形、菱形、正方形的判定小结一展身手1、在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BCC ①、对角线相等的菱形是正方形 ②、对角线互相垂直的矩形是正方形③、对角线互相垂直且相等的四边
形是正方形④ 四条边都相等的四边形是正方形⑤、四个角都相等的四边形是正方形⑥、四边相等,有一个角是直角的四
边形是正方形. ( )( )( )( )( )( )判断下列命题哪些是真命题、哪些是假命题? 真真假假假真例3、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB。求证:四边形CEDF是正方形。∴四边形ABCD是正方形( )∴ DE=DF( )DE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形( )而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥BC有三个角是直角的四边形是矩形角平分线的定理有一组邻边相等的矩形是正方形7.如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D。DE⊥AC,DF⊥AB。求证:四边形CEDF为正方形ABCDEFG证明:过点D作DG⊥AB,垂足为G
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB
∴ DE=DG
同理:DG=DF
∴ED=DF
∵ DE⊥AC,DF⊥AB
∴∠DEC= ∠DFC=90 °
又∵ ∠C=90 °
∴四边形ADFC是矩形
∴四边形ADFC是正方形谢谢合作!
