18.2.1矩形课件(35张)
文档属性
| 名称 | 18.2.1矩形课件(35张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1018.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-27 00:00:00 | ||
图片预览



文档简介
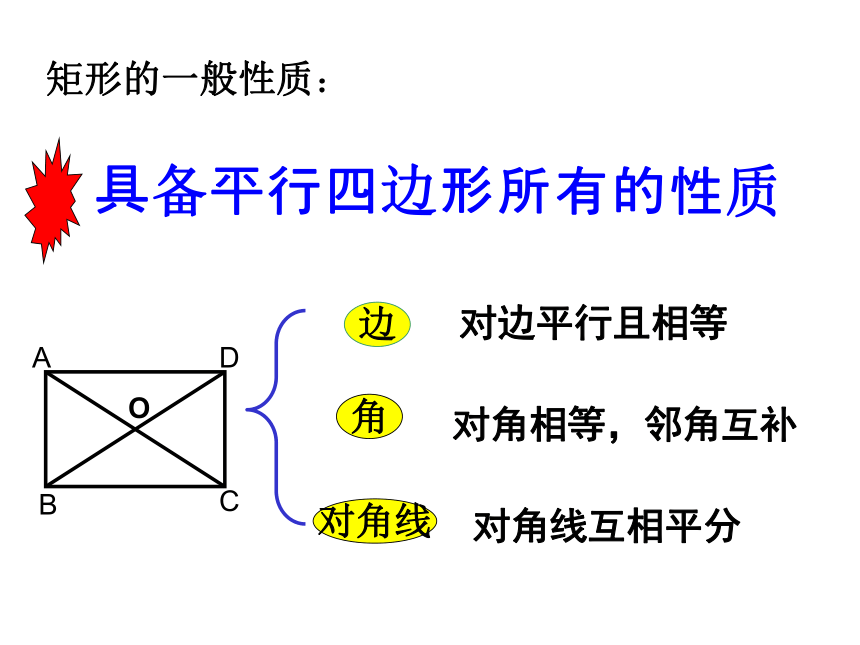
课件35张PPT。18.2 特殊的平行四边形18.2.1 矩形有一个角是直角的平行四边形是矩形矩形的定义:对边平行且相等对角相等,邻角互补对角线互相平分矩形的一般性质:探索新知:
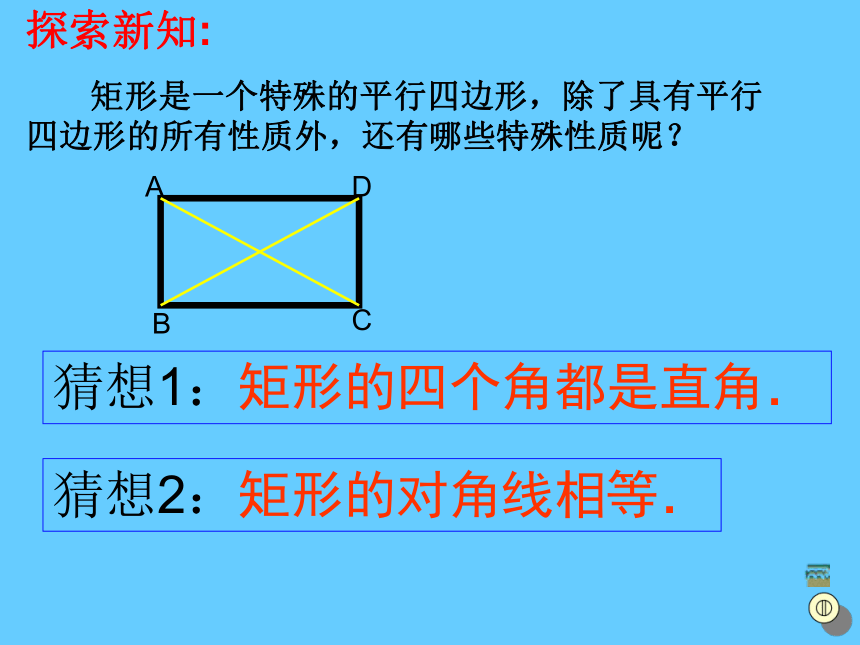
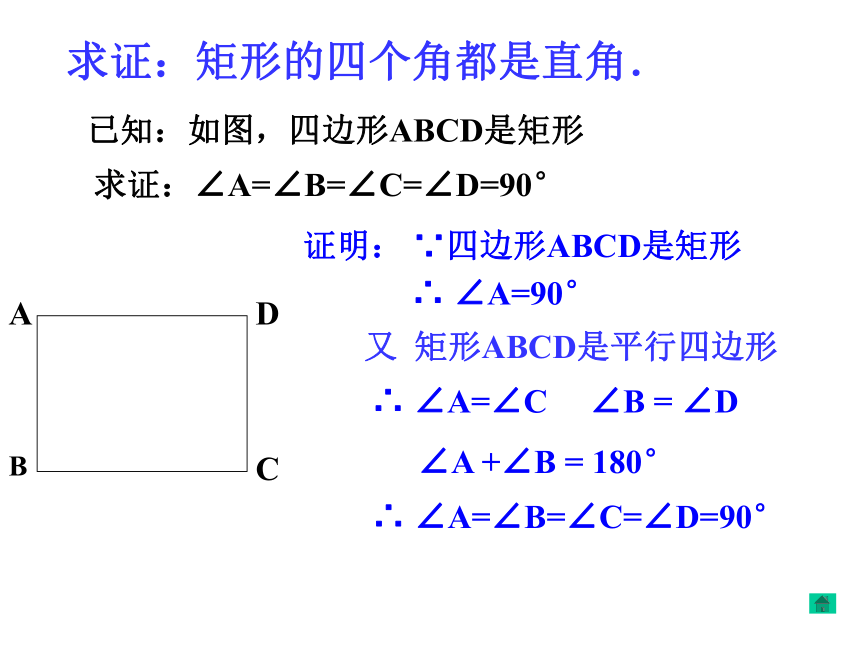
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
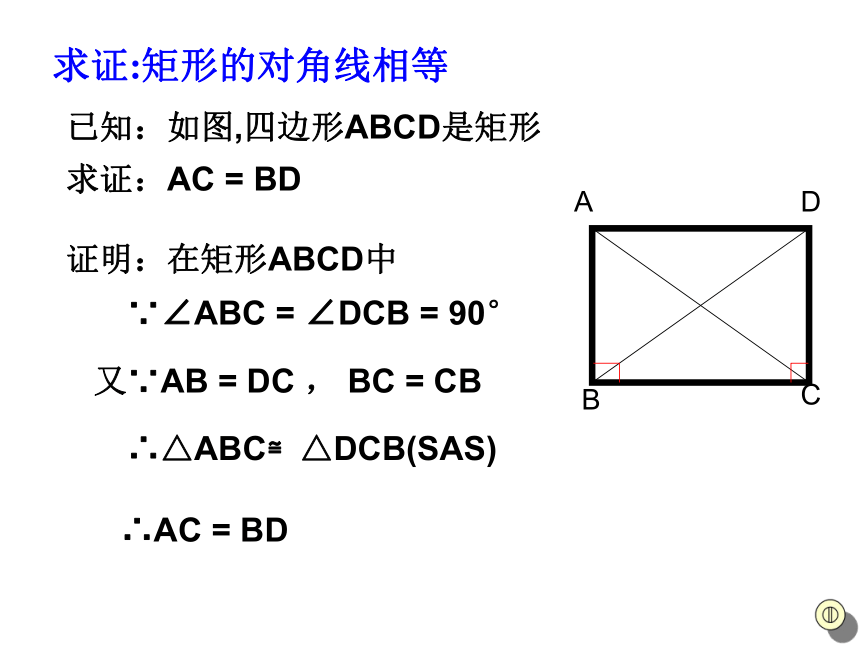
已知:如图,四边形ABCD是矩形
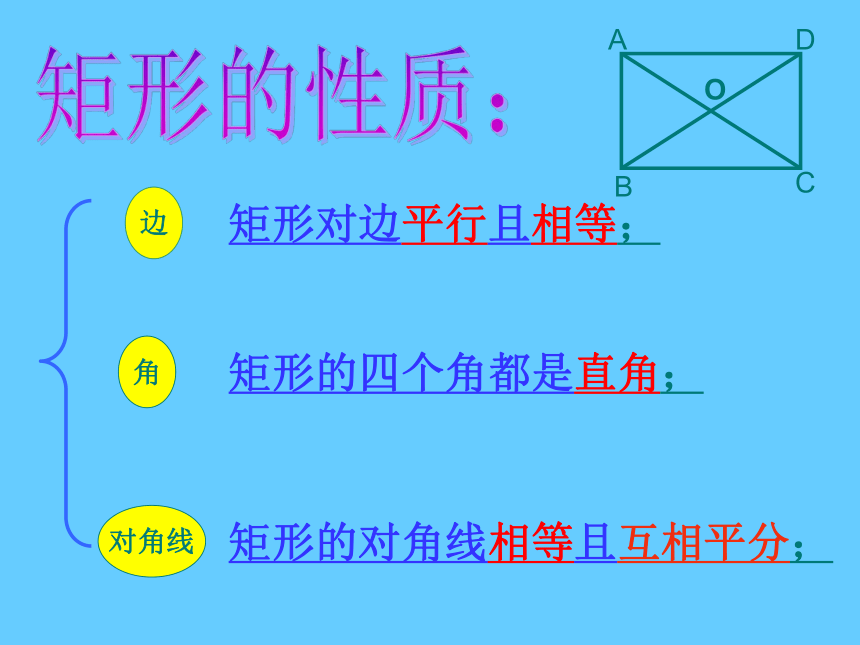
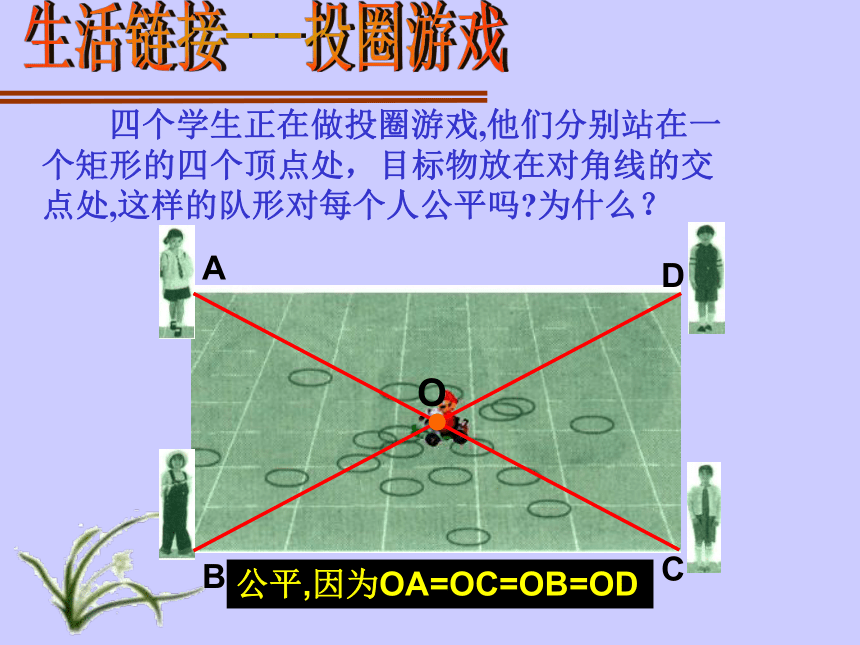
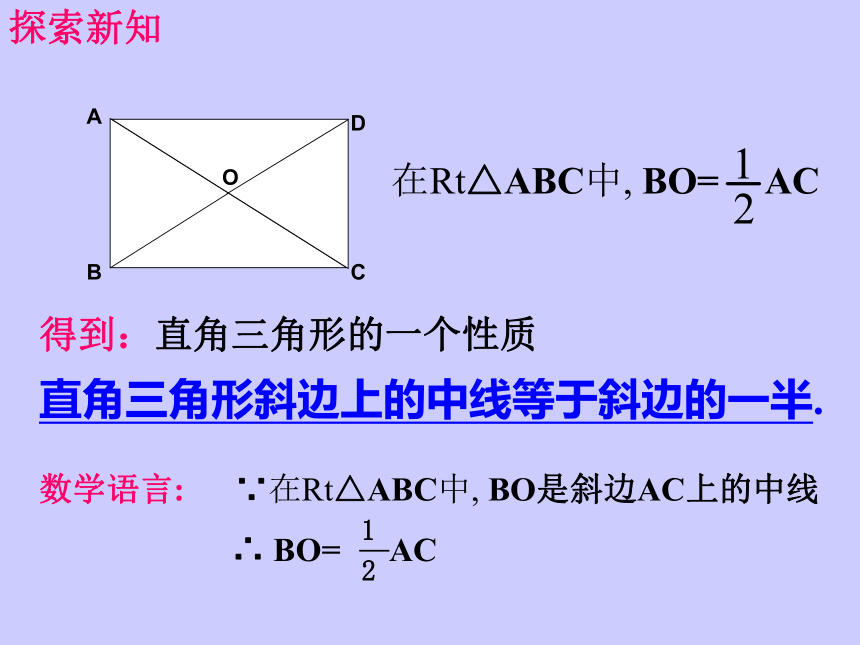
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB(SAS)∴AC = BD 求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的特殊性质矩形的四个角都是直角数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且互相平分;OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏ABCO得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.在Rt△ABC中, BO= AC探索新知例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. ∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ ,OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm,AB= _____cm5104营中寻宝4.已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线(1)若BD=3㎝,则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510营中寻宝复习回顾四边形定义:有一个角是直角的平行四边形叫做矩形。2018年12月15日星期六1你知道如何判定一个平行四边形是矩形吗?矩形的定义:有一个角是直角的平行四边形是矩形。你还有其它的判定方法吗?∠A=900四边形ABCD是矩形如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?AC=BDAC=BD都不是矩形想一想O如果一个平行四边形的对角线变成相等呢?将AC同时向两边拉长,使AC=BD想一想猜猜看:情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。命题:对角线相等的平行四边形是矩形。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形∴ ∠ABC=∠DCB∵ 四边形ABCD是平行四边形∴AB=CD对角线相等的平行四边形是矩形 。矩形的判定方法:几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)有一个角是直角
有两个角是直角 的 四边形是矩形吗?
有三个角是直角
探究情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。证明:∵ ∠A=∠B=90°∴ ∠A+∠B=180°∴AD∥BC同理可证:AB∥CD∴四边形ABCD是平行四边形又∵ ∠A=90°∴四边形ABCD是矩形矩形的判定方法:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形几何语言:小结:矩形的判定方法有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:下列各句判定矩形的说法是否正确? (1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX例2、如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD, ∠OAD=50°,
求∠OAB的度数解:∵四边形ABCD是平行四边形又∵OA=OD∴AC=BD∴四边形ABCD是矩形∴∠DAB=90°
又∠OAD=50°∴∠OAB=40°
1:如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形。 要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。2:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形. 1、已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是______;
(2)试用理由说明你的猜想.相等且互相平分3: 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.有一角为直角对角线相等有三个角是直角的四边形五种判定方法四边形小结:矩形的判定方法:矩形对角线互相平分且相等
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形∴ ∠A=90°又 矩形ABCD是平行四边形∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB(SAS)∴AC = BD 求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:矩形的特殊性质矩形的四个角都是直角数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900矩形的特殊性质矩形的对角线相等数学语言∵四边形ABCD是矩形 ∴AC = BD边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且互相平分;OABCD公平,因为OA=OC=OB=OD生活链接---投圈游戏ABCO得到:直角三角形的一个性质
直角三角形斜边上的中线等于斜边的一半.在Rt△ABC中, BO= AC探索新知例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形. ∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形 矩形具有而一般平行四边形不
具有的性质是 ( ) B.对边相等C营中热身已知:四边形ABCD是矩形
1.若已知AB=8㎝,AD=6㎝,
则AC=_______ ㎝ ,OB=_______ ㎝
2.若已知 ∠DOC=120°,AC=8㎝,则AD= _____cm,AB= _____cm5104营中寻宝4.已知△ABC是Rt△,∠ABC=900,BD是斜边AC上的中线(1)若BD=3㎝,则AC= ㎝
(2) 若∠C=30°,AB=5㎝,则AC= ㎝,
BD= ㎝.6510营中寻宝复习回顾四边形定义:有一个角是直角的平行四边形叫做矩形。2018年12月15日星期六1你知道如何判定一个平行四边形是矩形吗?矩形的定义:有一个角是直角的平行四边形是矩形。你还有其它的判定方法吗?∠A=900四边形ABCD是矩形如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?AC=BDAC=BD都不是矩形想一想O如果一个平行四边形的对角线变成相等呢?将AC同时向两边拉长,使AC=BD想一想猜猜看:情境一:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?猜想:对角线相等的平行四边形是矩形 。命题:对角线相等的平行四边形是矩形。已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB(SSS)∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形∴ ∠ABC=∠DCB∵ 四边形ABCD是平行四边形∴AB=CD对角线相等的平行四边形是矩形 。矩形的判定方法:几何语言:∵四边形ABCD是平行四边形
AC=BD∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)有一个角是直角
有两个角是直角 的 四边形是矩形吗?
有三个角是直角
探究情境一:李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。证明:∵ ∠A=∠B=90°∴ ∠A+∠B=180°∴AD∥BC同理可证:AB∥CD∴四边形ABCD是平行四边形又∵ ∠A=90°∴四边形ABCD是矩形矩形的判定方法:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形几何语言:小结:矩形的判定方法有一个角是直角的平行四边形是矩形。对角线相等的平行四边形是矩形 。(对角线相等且互相平分的四边形是矩形。)有三个角是直角的四边形是矩形 。方法1:方法2:方法3:下列各句判定矩形的说法是否正确? (1)对角线相等的四边形是矩形;(2)对角线互相平分且相等的四边形是矩形;(3)有一个角是直角的四边形是矩形;(5)有三个角是直角的四边形是矩形;(6)四个角都相等的四边形是矩形;(7)对角线相等,且有一个角是直角的四边形是矩形;(10)一组邻边垂直,一组对边平行且相等的四边形是矩形;(9)对角线相等且互相垂直的四边形是矩形;(8)一组对角互补的平行四边形是矩形;(4)有三个角都相等的四边形是矩形;XXXX例2、如图,在 ABCD中,对角线AC,BD相交于点O,且OA=OD, ∠OAD=50°,
求∠OAB的度数解:∵四边形ABCD是平行四边形又∵OA=OD∴AC=BD∴四边形ABCD是矩形∴∠DAB=90°
又∠OAD=50°∴∠OAB=40°
1:如图,M为平行四边形ABCD边AD的中点,且MB=MC,
求证:四边形ABCD是矩形。 要判定一个四边形是矩形,通常先判定它是平行四边形,再根据平行四边形构成矩形的条件,判定有一个角是直角或者对角线相等。2:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形. 1、已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
(1)猜想AC和BD间的关系是______;
(2)试用理由说明你的猜想.相等且互相平分3: 如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.有一角为直角对角线相等有三个角是直角的四边形五种判定方法四边形小结:矩形的判定方法:矩形对角线互相平分且相等
