3.4实际问题与一元一次方程 强化训练 (含简单答案) 2023-2024学年人教版七年级数学上册
文档属性
| 名称 | 3.4实际问题与一元一次方程 强化训练 (含简单答案) 2023-2024学年人教版七年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 248.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 08:35:36 | ||
图片预览



文档简介
3.4实际问题与一元一次方程
一、单选题
1.用一根绳子环绕一棵大树,若环绕大树3周绳子还多4米,若环绕4周又少了3米,则环绕大树一周需要绳子长( )
A.5米 B.6米 C.7米 D.8米
2.某校在举办“读书月”的活动中,将一些图书分给了七年一班的学生阅读.如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设该校七年一班有学生人,则下列方程正确的( )
A. B.
C. D.
3.星期天,小明一家从家里出发去爷爷家,妈妈骑自行车先走,速度为10千米/时,40分钟后爸爸开车和小明一起出发,速度为60千米/时,结果3人同时到达爷爷家,则小明家距爷爷家的路程为( )
A.8千米 B.10千米 C.12千米 D.15千米
4.七年级(1)班有30人会下象棋或围棋,已知会下象棋的人数比会下围棋的人数多5人,两种棋都会下的有17人,问只会下围棋的有多少人 设只会下围棋的有人,可得方程
A. B.
C. D.
5.设有x个人共种a棵树苗,如果每人种6棵,则剩下4棵树苗未种;如果每人种8棵,则缺2棵树苗.根据题意,列方程正确的是( )
A.﹣4=+2 B.+4=﹣2 C.= D.=
6.如图是年月份的月历,在月历上任意圈出一个正方形,则下列等式中错误的是( )
A. B. C. D.
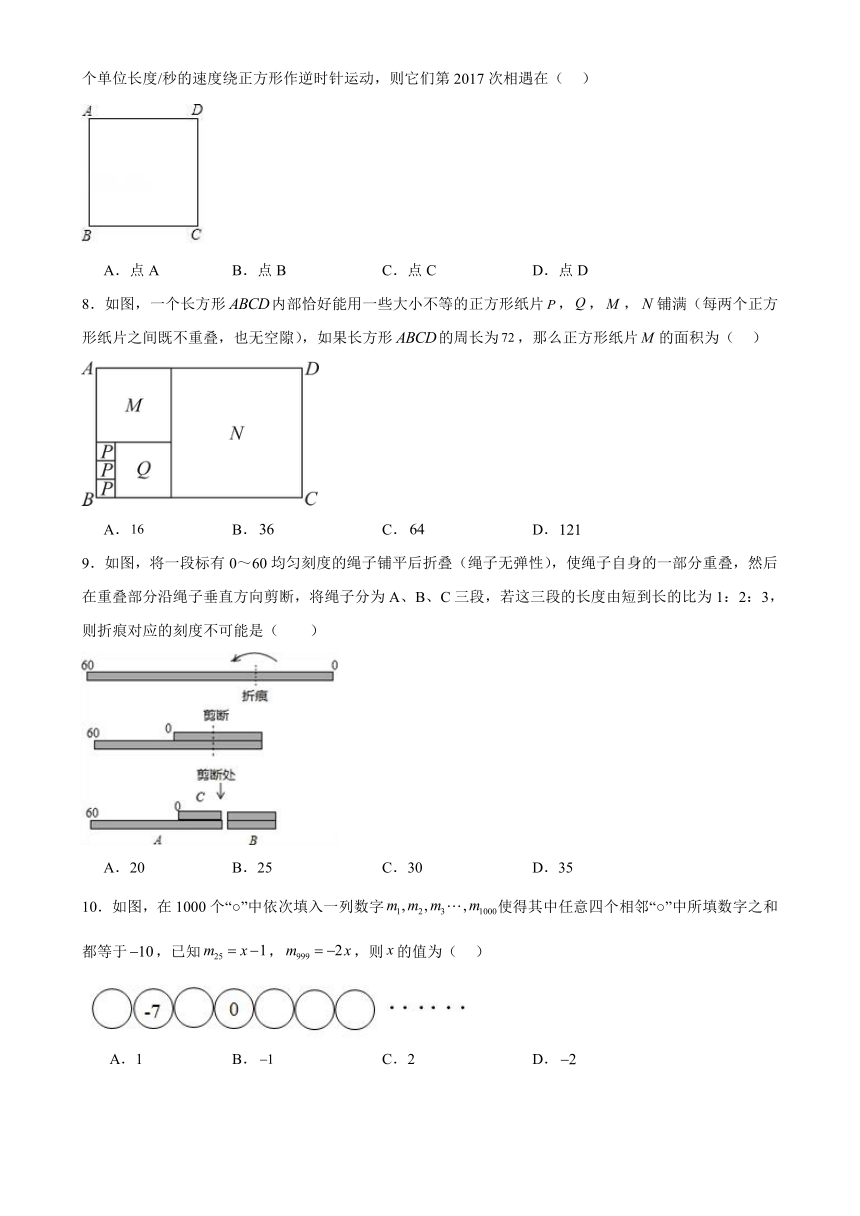
7.如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以
个单位长度/秒的速度绕正方形作逆时针运动,则它们第2017次相遇在( )
A.点A B.点B C.点C D.点D
8.如图,一个长方形内部恰好能用一些大小不等的正方形纸片,,,铺满(每两个正方形纸片之间既不重叠,也无空隙),如果长方形的周长为,那么正方形纸片的面积为( )
A. B. C. D.
9.如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
A.20 B.25 C.30 D.35
10.如图,在1000个“○”中依次填入一列数字使得其中任意四个相邻“○”中所填数字之和都等于,已知,,则的值为( )
A.1 B. C.2 D.
二、填空题
11.2013年11月9日是一年一度的中国消防宣传日,某中学七年级(1)、(2)、(3)班的学生去人民广场当消防宣传志愿者,七年级(1)班去了a个人,七年级(2)班去的人数比(1)班的2倍还多8人,七年级(3)班去的人数比(2)班的一半少6人,当七年级(1)班去了20人时,三个班总共有 人去当消防宣传志愿者.
12.《孙子算经》中有一个问题:“今有三人共车,二车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人乘车,如果每3人共乘一辆车,则空2辆车;如果每2人共乘一辆车,则有9个人无车可乘.如果设一共有人,根据条件,可列方程为 .
13.如图,正方形的边长是4cm,剪去四个角后成为一个正八边形,这个正八边形的面积是
14.某电视台组织知识竞赛,共设有20道单项选择题,各题分值相同,每题必答.下表记录了3个参赛者的得分情况.
参赛者 答对题数 得分
A 18 88
B 20 100
C 10 40
如果参赛者D得70分,则他答对的题数为 .
15.如图,圆柱形容器的底面半径为,高为.其里面盛有深的水,将底面半径为,高为的圆柱形铁块沉入水中,此时容器内的水面高度上升了 .
16.我们见过的足球大多是由许多小黑白块的牛皮缝合而成的.初一年级的李强和王开两位同学,在踢足球的休息之余研究足球的黑白块的块数.结果发现黑块均呈五边形,白块呈六边形.由于球体上黑白相间,李强好不容易数清了黑块共12块,王开数白块时不是重复,就是遗漏,无法数清白块的块数,请你利用数学知识帮助他们求出白块的块数为 块.
三、解答题
17.一个晒盐场用海水可以晒出盐.照这样计算,如果一块盐田一次放入585000吨海水,可以晒出几吨盐?多少吨海水可以晒出9吨盐?
18.某文具店今年1月份购进一批笔记本,共2290本.每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量为2200本,则2月份售价多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比2月份在(1)的条件下的售价减少了,结果3月份的销量比2月份在(1)的条件下的销售量增加了50%,3月份的销售利润达到6600元,求的值.
19.如图,长方形ABCD被分成六个小的正方形,已知中间一个小正方形的边长为2,其它正方形的边长分别为.观察图形并探索:
(1)填空: , ;(用含的代数式表示)
(2)求的值.
20.如图,已知数轴上原点为0,点表示的数为,A在的右边,且A与的距离是5,动点从点出发,以每秒3个单位长度的速度沿数轴向右匀速运动,动点从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点,同时出发,设运动时间为秒.
(1)写出数轴上点A表示的数 ,点表示的数 (用含的代数式表示),点表示的数 (用含的代数式表示);
(2)问点与点何时到点的距离相等?
(3)若点是数轴上一点,点表示的数是,是否存在,使得?如果存在,直接写出的值;如果不存在,请说明理由;
(4)若点到达点后,立即折返去追,能追上吗?此时距离原点有多远?(直接写出距离即可)
参考答案:
1.C
2.B
3.A
4.D
5.D
6.D
7.B
8.C
9.C
10.C
11.86.
12.
13.
14.15
15.0.18
16.20
17.可以晒出17550吨盐,300吨海水可以晒出9吨盐
18.(1)14元;(2)50.
19.(1),;(2)8
20.(1)3;;
(2)秒或1秒
(3)存在,或
(4)能追上,此时距离原点有13个单位
一、单选题
1.用一根绳子环绕一棵大树,若环绕大树3周绳子还多4米,若环绕4周又少了3米,则环绕大树一周需要绳子长( )
A.5米 B.6米 C.7米 D.8米
2.某校在举办“读书月”的活动中,将一些图书分给了七年一班的学生阅读.如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设该校七年一班有学生人,则下列方程正确的( )
A. B.
C. D.
3.星期天,小明一家从家里出发去爷爷家,妈妈骑自行车先走,速度为10千米/时,40分钟后爸爸开车和小明一起出发,速度为60千米/时,结果3人同时到达爷爷家,则小明家距爷爷家的路程为( )
A.8千米 B.10千米 C.12千米 D.15千米
4.七年级(1)班有30人会下象棋或围棋,已知会下象棋的人数比会下围棋的人数多5人,两种棋都会下的有17人,问只会下围棋的有多少人 设只会下围棋的有人,可得方程
A. B.
C. D.
5.设有x个人共种a棵树苗,如果每人种6棵,则剩下4棵树苗未种;如果每人种8棵,则缺2棵树苗.根据题意,列方程正确的是( )
A.﹣4=+2 B.+4=﹣2 C.= D.=
6.如图是年月份的月历,在月历上任意圈出一个正方形,则下列等式中错误的是( )
A. B. C. D.
7.如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以
个单位长度/秒的速度绕正方形作逆时针运动,则它们第2017次相遇在( )
A.点A B.点B C.点C D.点D
8.如图,一个长方形内部恰好能用一些大小不等的正方形纸片,,,铺满(每两个正方形纸片之间既不重叠,也无空隙),如果长方形的周长为,那么正方形纸片的面积为( )
A. B. C. D.
9.如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
A.20 B.25 C.30 D.35
10.如图,在1000个“○”中依次填入一列数字使得其中任意四个相邻“○”中所填数字之和都等于,已知,,则的值为( )
A.1 B. C.2 D.
二、填空题
11.2013年11月9日是一年一度的中国消防宣传日,某中学七年级(1)、(2)、(3)班的学生去人民广场当消防宣传志愿者,七年级(1)班去了a个人,七年级(2)班去的人数比(1)班的2倍还多8人,七年级(3)班去的人数比(2)班的一半少6人,当七年级(1)班去了20人时,三个班总共有 人去当消防宣传志愿者.
12.《孙子算经》中有一个问题:“今有三人共车,二车空;二人共车,九人步,问人与车各几何?”意思是:现有若干人乘车,如果每3人共乘一辆车,则空2辆车;如果每2人共乘一辆车,则有9个人无车可乘.如果设一共有人,根据条件,可列方程为 .
13.如图,正方形的边长是4cm,剪去四个角后成为一个正八边形,这个正八边形的面积是
14.某电视台组织知识竞赛,共设有20道单项选择题,各题分值相同,每题必答.下表记录了3个参赛者的得分情况.
参赛者 答对题数 得分
A 18 88
B 20 100
C 10 40
如果参赛者D得70分,则他答对的题数为 .
15.如图,圆柱形容器的底面半径为,高为.其里面盛有深的水,将底面半径为,高为的圆柱形铁块沉入水中,此时容器内的水面高度上升了 .
16.我们见过的足球大多是由许多小黑白块的牛皮缝合而成的.初一年级的李强和王开两位同学,在踢足球的休息之余研究足球的黑白块的块数.结果发现黑块均呈五边形,白块呈六边形.由于球体上黑白相间,李强好不容易数清了黑块共12块,王开数白块时不是重复,就是遗漏,无法数清白块的块数,请你利用数学知识帮助他们求出白块的块数为 块.
三、解答题
17.一个晒盐场用海水可以晒出盐.照这样计算,如果一块盐田一次放入585000吨海水,可以晒出几吨盐?多少吨海水可以晒出9吨盐?
18.某文具店今年1月份购进一批笔记本,共2290本.每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量为2200本,则2月份售价多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比2月份在(1)的条件下的售价减少了,结果3月份的销量比2月份在(1)的条件下的销售量增加了50%,3月份的销售利润达到6600元,求的值.
19.如图,长方形ABCD被分成六个小的正方形,已知中间一个小正方形的边长为2,其它正方形的边长分别为.观察图形并探索:
(1)填空: , ;(用含的代数式表示)
(2)求的值.
20.如图,已知数轴上原点为0,点表示的数为,A在的右边,且A与的距离是5,动点从点出发,以每秒3个单位长度的速度沿数轴向右匀速运动,动点从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点,同时出发,设运动时间为秒.
(1)写出数轴上点A表示的数 ,点表示的数 (用含的代数式表示),点表示的数 (用含的代数式表示);
(2)问点与点何时到点的距离相等?
(3)若点是数轴上一点,点表示的数是,是否存在,使得?如果存在,直接写出的值;如果不存在,请说明理由;
(4)若点到达点后,立即折返去追,能追上吗?此时距离原点有多远?(直接写出距离即可)
参考答案:
1.C
2.B
3.A
4.D
5.D
6.D
7.B
8.C
9.C
10.C
11.86.
12.
13.
14.15
15.0.18
16.20
17.可以晒出17550吨盐,300吨海水可以晒出9吨盐
18.(1)14元;(2)50.
19.(1),;(2)8
20.(1)3;;
(2)秒或1秒
(3)存在,或
(4)能追上,此时距离原点有13个单位
