2023—2024学年人教版九年级数学上册 第二十四章圆单元达标分层练习题 (含解析)
文档属性
| 名称 | 2023—2024学年人教版九年级数学上册 第二十四章圆单元达标分层练习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 801.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 08:37:33 | ||
图片预览


文档简介
人教版九年级数学上册第二十四章圆单元达标分层练习题
一、选择题
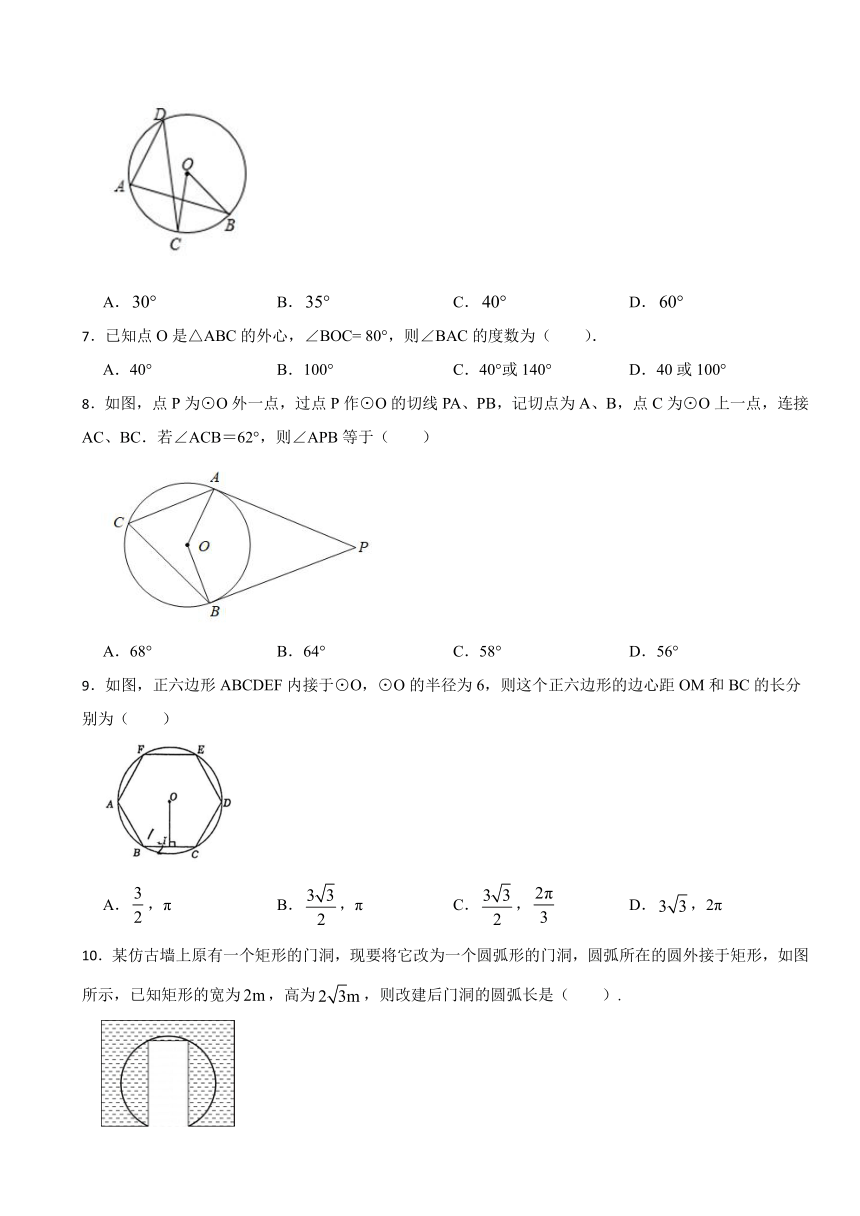
1.如图,圆周角∠ACB =48°,则圆心角∠AOB的度数为( ).
A.48° B.24° C.96° D.90°
2.如图,AB是⊙O的直径,弦CD⊥AB于点E.若OC=5 cm,CD=6 cm,则AE=( ).
A.4cm B.3cm C.9cm D.8cm
3.下列命题为真命题的是( ).
A.三点确定一个圆
B.度数相等的弧相等
C.90°的圆周角所对的弦是直径
D.相等的圆心角所对的弧相等,所对的弦也相等
4.已知⊙O的半径是6,点A到圆心O的距离是5,则点A与⊙O的位置关系是( ).
A.点A在⊙O上 B.点A在⊙O内
C.点A在⊙O外 D.点A与圆心O重合
5.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( ).
A.45° B.50° C.60° D.75°
6. 如图,是的弦,半径,为圆周上一点,若所对应圆心角的度数为,则的度数为( )
A. B. C. D.
7.已知点O是△ABC的外心,∠BOC= 80°,则∠BAC的度数为( ).
A.40° B.100° C.40°或140° D.40或100°
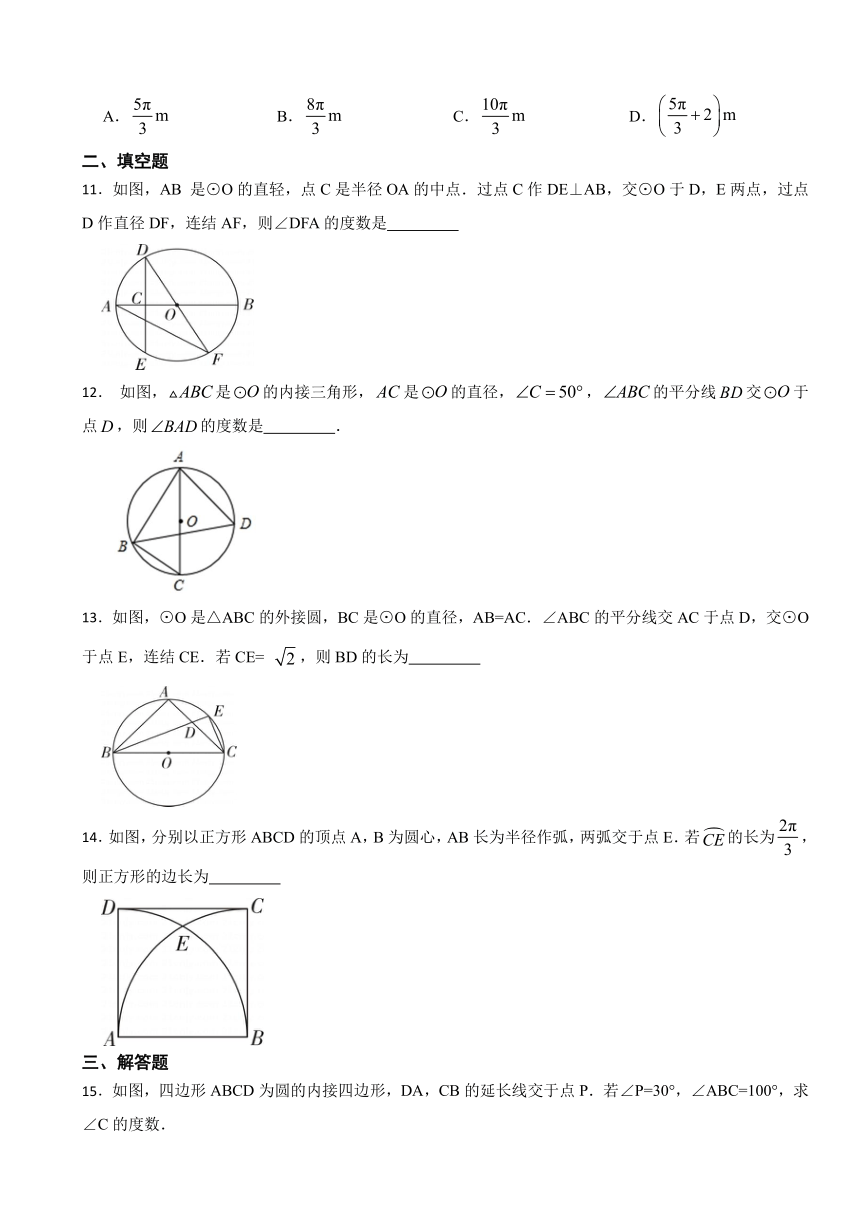
8.如图,点P为⊙O外一点,过点P作⊙O的切线PA、PB,记切点为A、B,点C为⊙O上一点,连接AC、BC.若∠ACB=62°,则∠APB等于( )
A.68° B.64° C.58° D.56°
9.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM和BC的长分别为( )
A.,π B.,π C., D.,2π
10.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图所示,已知矩形的宽为,高为,则改建后门洞的圆弧长是( ).
A. B. C. D.
二、填空题
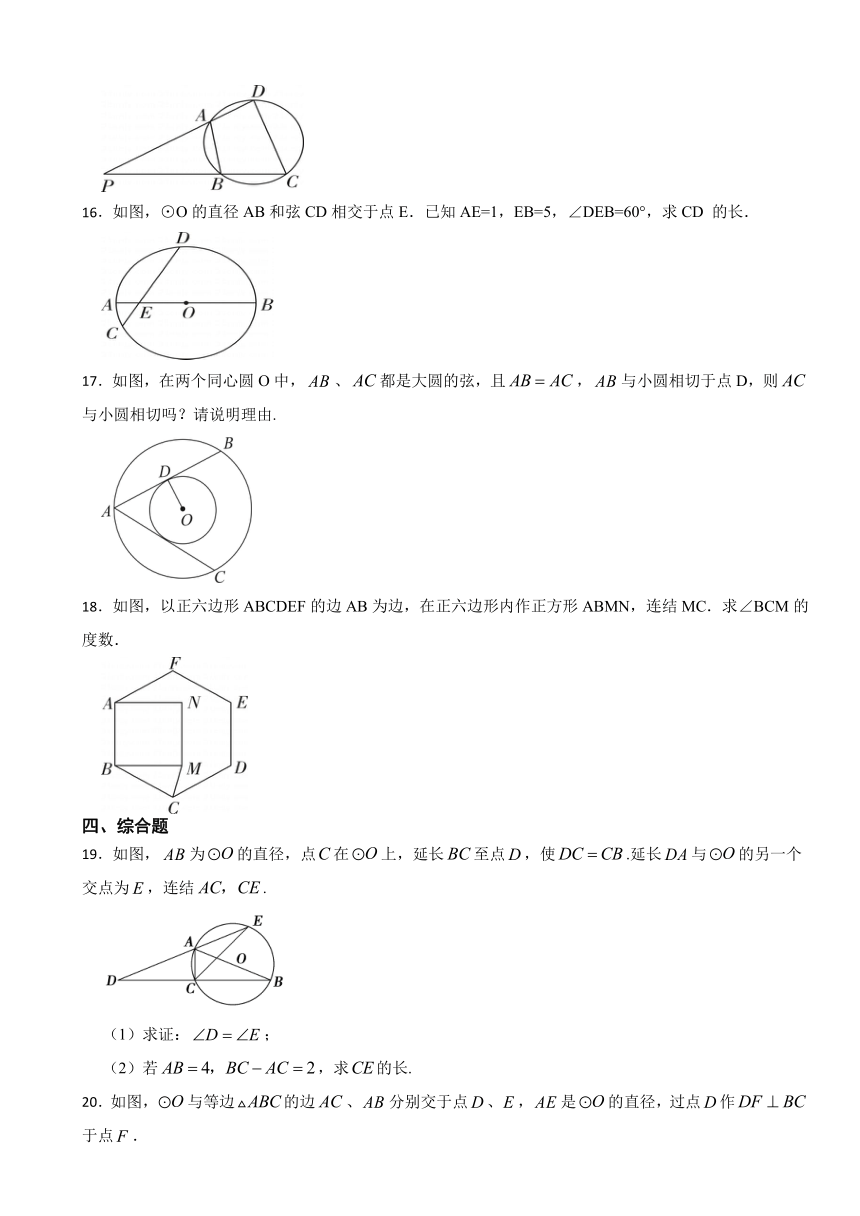
11.如图,AB 是⊙O的直轻,点C是半径OA的中点.过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA的度数是
12. 如图,是的内接三角形,是的直径,,的平分线交于点,则的度数是 .
13.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= ,则BD的长为
14.如图,分别以正方形ABCD的顶点A,B为圆心,AB长为半径作弧,两弧交于点E.若的长为,则正方形的边长为
三、解答题
15.如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P.若∠P=30°,∠ABC=100°,求∠C的度数.
16.如图,⊙O的直径AB和弦CD相交于点E.已知AE=1,EB=5,∠DEB=60°,求CD 的长.
17.如图,在两个同心圆O中,、都是大圆的弦,且,与小圆相切于点D,则与小圆相切吗?请说明理由.
18.如图,以正六边形ABCDEF的边AB为边,在正六边形内作正方形ABMN,连结MC.求∠BCM的度数.
四、综合题
19.如图,为的直径,点在上,延长至点,使.延长与的另一个交点为,连结.
(1)求证:;
(2)若,求的长.
20.如图,与等边的边、分别交于点、,是的直径,过点作于点.
(1)求证:是的切线:
(2)已知的半径为3,连接,当等边的边长为多少时,与相切?
21.如图,圆中延长弦,交于点,连接,,,.
(1)若,,求的度数;
(2)若,,,判断,,满足什么数量关系时,?请说明理由.
22.如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,点E是BC的中点,连结并延长OE交圆于点D.
(1)求证:ODAC.
(2)若DE=2,BE=2,求阴影部分的面积.
答案解析部分
1.【答案】C
【解析】【解答】解:如图可知,∠ACB和∠AOB在同一圆中,且所对的弧均为弧AB. 根据圆周角定理可知,∠AOB=2∠ACB=2×48°=96°.
故答案为:C.
【分析】根据圆周角定理可知,在同一圆中,同弧所对的圆周角等于圆心角的一半.
2.【答案】C
【解析】【解答】解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴
在中,
∴.
故答案为:C.
【分析】根据垂径定理求出CE的长,结合勾股定理即可得到OE的长,最后根据线段间的数量关系即可求解.
3.【答案】C
【解析】【解答】解: A、不在一条直线上的三点确定一个圆 ,故不符合题意;
B、 能够互相重合的弧叫做等弧,故不符合题意;
C、 90°的圆周角所对的弦是直径 ,故符合题意;
D、 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,故不符合题意.
故答案为:C.
【分析】根据确定圆的条件,圆周角定理、弧弦圆心角的关系、等弧的定义逐项判断即可.
4.【答案】B
【解析】【解答】解:∵ ⊙O的半径是6,点A到圆心O的距离是5 ,
∴A到圆心O的距离小于⊙O的半径,
∴点A在⊙O内 ,
故答案为:B.
【分析】设⊙O的半径为r,点到圆心O的距离为d,当d<r时,点在圆内;当d=r时,点在圆上,当d>r时,点在圆外,据此判断即可.
5.【答案】C
【解析】【解答】解:∵四边形ABCO是平行四边形,
∴∠AOC=∠ABC,
∵四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
而∠ADC=∠AOC,
∴2∠ADC+∠ADC=180°,解得:∠ADC=60°.
故答案为:C.
【分析】由平行四边形的对角相等可得∠AOC=∠ABC,由圆圆内接四边形的对角互补可得∠ADC+∠ABC=180°然后根据圆周角定理可得关于∠ADC的方程,解方程可求解.
6.【答案】B
【解析】【解答】∵半径,所对应圆心角的度数为,
∴,
∴∠AOC=∠BOC=70°,
∵,
∴∠ADC=∠AOC=35°,
故答案为:B.
【分析】先利用垂径定理可得,再利用圆周角的性质可得∠ADC=∠AOC=35°.
7.【答案】C
【解析】【解答】解:分两种情况,
①△ABC为锐角三角形时,
∵
∴
②△ABC为钝角三角形,
在优弧BC上任取一点P,连接BP,CP,
∵
∴
∴
综上所述,∠BAC的度数为:40°,140°,
故答案为:C.
【分析】根据题意可知需分两种情况讨论:①△ABC为锐角三角形,②△ABC为钝角三角形,分别根据圆周角定理和圆内接四边形的性质,即可求解.
8.【答案】D
【解析】【解答】解:∵ 圆周角∠ACB=62°
∴(圆周角的度数等于它所对弧上的圆心角度数的一半)
∴
∵PA、PB是⊙O的切线 ,
∴
∴P、A、B、O四点共圆(四边形对角互补,那么四点共圆)
∴(圆的内接四边形对角和是180度)
∴
故答案为:D
【分析】圆周角的度数等于它所对弧上的圆心角度数的一半,这是圆周角定理;圆的内接四边形对角和是180度,反过来四边形对角和是180°那么四点共圆,这两个定理都是有关圆的角度证明时经常用到的。
9.【答案】D
10.【答案】C
【解析】【解答】解:如图,矩形内接于,连接、,
四边形是矩形,
,
为的直径,
,,
,,
,
,
.
故答案为:.
【分析】先利用矩形的性质和圆周角定理证得AC是直径,再通过直角三角形的性质得到的度数,从而求得的度数,接着利用弧长的计算公式求得改建后门洞的圆弧长.
11.【答案】30°
【解析】【解答】解:∵ 点C是半径OA的中点.DE⊥AB ,
∴OD=2OC,∠DCO=90°,
∴∠D=30°,
∴∠AOD=90°-30°=60°,
∴ ∠DFA =∠AOD=30°,
故答案为:30°,
【分析】由题意得OD=2OC,利用直角三角形的性质可得∠D=30°,从而求出∠AOD=60°,再根据圆周角定理求解即可.
12.【答案】
【解析】【解答】解:
∵AC是直径,∴∠ABC=90°,
∵BD平分∠ABC,∴∠ABD=45°,
又∵∠D=∠C=50°
∴∠BAD=180°-∠ABD-∠D=180°-45°-50°=85°。
故答案为:85°
【分析】直径所对的圆周角是90°,同弧所对的圆周角相等,由此可得出∠ABC和∠D的度数,再根据内角和定理求出∠BAD。
13.【答案】
【解析】【解答】解:如图,延长BA,CE,交于点M.
∵BC是⊙O的直径,
∴∠BAD=∠CAM=90°,∠BEC=∠BEM=90°,
又AB=AC,∠ABD=∠ACM,
∴△ABD≌△ACM,
∴BD=CM.
由∠EBM=∠EBC,BE= BE,∠BEC=∠BEM,得△BEC≌△BEM,
∴EC=EM,
∴BD=CM=2CE=.
【分析】延长BA,CE,交于点M,证明△ABD≌△ACM(ASA),可得BD=CM.再证△BEC≌△BEM(ASA),可得EC=EM,根据BD=CM=2CE即可求解.
14.【答案】4
15.【答案】解:∵四边形ABCD为圆的内接四边形,
∴∠D+∠ABC=180°,
∵∠ABC=100°,∴∠D=180°-100°=80°,
∵∠P=30°,
∴∠C=180°-30°-80°=70°.
【解析】【分析】根据圆内接四边形的性质可求出∠D的度数,然后在三角形PCD中,用三角形内角和定理可求解.
16.【答案】解:作OF⊥CD于点F ,连结OD,
AB=AE+ BE =6,即⊙O的半径为3.
在Rt△OEF中,OE=OA-AE=3-1=2,∠DEB=60° ,则∠EOF=30° ,OF= ,
在Rt△ODF中,DF= ,
∴CD=2DF= .
【解析】【分析】作OF⊥CD于点F , 连结OD, 先求出 ⊙O 的半径,再根据勾股定理求出OF和DF的长,最后利用垂径定理求出CD的长.
17.【答案】解:过点O作于E,设小圆与的切点为D,连接,如图,
由切线性质可知,
由垂径定理可知,
∵,
∴,
在和中,,
∴,
∴,
∴与小圆相切.
【解析】【分析】 过点O作OE⊥AC于E,设小圆与AB的切点为D,连接OD、OA,由切线性质可知OD⊥AB, 由垂径定理可知AD=DB,AE=EC,结合AB=AC可得AD=AE,利用HL证明Rt△ AEO≌Rt△ADO,得到OE=OD,据此证明.
18.【答案】解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90° ,AB= BM.
∴∠MBC=120°-90°=30,BM=BC.
∴∠BCM=∠BMC=×(180°-30°)=75°.
【解析】【分析】利用正六边形的性质,可证得∠ABC=120°,AB=BC,利用正方形的性质可推出∠ABM=90° ,AB= BM;再求出∠MBC的度数,同时可证得BM=BC,然后利用等腰三角形的性质和三角形的内角和定理求出∠BCM的度数.
19.【答案】(1)证明:为的直径,
,
,
,
在和中,
,
,
,
,
;
(2)解:设,
,
,
在中,由勾股定理可得,
即,
解得:,(舍去),
,
由(1)得:,
,
,
,
的长为.
【解析】【分析】(1)由圆周角定理可得∠ACB=90°,则∠ACD=180°-∠ACB=90°,由已知条件可知DC=BC,AC=AC,利用SAS证明△ACD≌△ACB,得到∠D=∠B,由圆周角定理可得∠B=∠E,据此证明;
(2)设BC=x,则AC=x-2,在Rt△ABC中,根据勾股定理可得x的值,由(1)得∠D=∠E,则CD=CE,结合DC=CB可得CE=CB,据此解答.
20.【答案】(1)证明:∵ 是等边三角形,
∴ ,
∵ ,
∴ 是等边三角形,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
又∵ 为 的半径,
∴ 是 的切线
(2)解:∵ 都是 的切线,
∴ ,
∵ 是等边三角形,
∴ ,
∴ ,
∴ ,
∴ ,
由(1)得 是等边三角形,
∴ ,
在 中, ,则 ,
∴ ,
∴ ,
∴当等边 的边长为9时, 与 相切.
【解析】【分析】(1)先证明,再结合OD是的半径,可得DF是的切线;
(2)根据切线的性质可得,再利用“AAS”证出,可得,再结合,证出 是等边三角形,最后求出即可。
21.【答案】(1)解:∵,,
∴∠ACB=∠ADB=60°,∠BCD=∠BAD=10°,
∴∠ACD=∠ACB+∠BCD=60°+10°=70°
(2)解:当γ=2(α+β)时,AD=CD,
∵,,
∴∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,
∴∠ACD=∠ACB+∠BCD=α°+β°,
∵AD=CD,
∴∠ACD=∠DAC,
∵,
∴∠CAD=∠CBD=∠ACD,
∵∠DBA+∠ACD=180°,∠EBD+∠DBA=180°,
∴∠ACD=∠EBD,
∴∠EBC=∠EBD+∠DBC=2∠ACD=γ°,
∴γ=2(α+β)
【解析】【分析】(1)利用同弧所对的圆周角相等,可求出∠ACB,∠BCD的度数,再根据∠ACD=∠ACB+∠BCD,代入计算求出∠ACD的度数.
(2)利用同弧所对的圆周角相等,可证得∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,可得到∠ACD=α°+β°,利用等边对等角可证得∠ACD=∠DAC,再利用圆周角定理可得到∠CAD=∠CBD=∠ACD,利用圆内接四边形的性质可得到∠ACD=∠EBD,由此可推出∠EBC=2∠ACD,即可证得结论.
22.【答案】(1)证明:如图连接OC,
∵OC=OB,点E为BC的中点,
∴OE⊥BC,
∴∠BEO=90°,
∵AB为圆的直径,
∴∠ACB=∠BEO=90°,
∴OD∥AC;
(2)解:连接OC,设圆的半径为r,则OE=r-2,
∵,
∴,
解得,
∴,
∴∠ABC=30°,
∴∠COA=60°,
由(1)可得,
∴,
∴,
∵△BOC与△AOC等底同高,
∴,
∴.
【解析】【分析】(1)连接OC,由等腰三角形的性质可得OE⊥BC,由AB为圆的直径,可得∠ACB=∠BEO=90°,根据平行线的判定即证;(2)连接OC,设圆的半径为r,则OE=r-2,由勾股定理知,据此建立关于r方程,求出r=4,由线段的中点可得OE=2,从而得出∠ABC=30°,继而得出∠COA=60°, 由(1)可得, 利用垂径定理可得,求出, 根据三角形等底同高可得, 根据,利用扇形的面积公式即可求解.
一、选择题
1.如图,圆周角∠ACB =48°,则圆心角∠AOB的度数为( ).
A.48° B.24° C.96° D.90°
2.如图,AB是⊙O的直径,弦CD⊥AB于点E.若OC=5 cm,CD=6 cm,则AE=( ).
A.4cm B.3cm C.9cm D.8cm
3.下列命题为真命题的是( ).
A.三点确定一个圆
B.度数相等的弧相等
C.90°的圆周角所对的弦是直径
D.相等的圆心角所对的弧相等,所对的弦也相等
4.已知⊙O的半径是6,点A到圆心O的距离是5,则点A与⊙O的位置关系是( ).
A.点A在⊙O上 B.点A在⊙O内
C.点A在⊙O外 D.点A与圆心O重合
5.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( ).
A.45° B.50° C.60° D.75°
6. 如图,是的弦,半径,为圆周上一点,若所对应圆心角的度数为,则的度数为( )
A. B. C. D.
7.已知点O是△ABC的外心,∠BOC= 80°,则∠BAC的度数为( ).
A.40° B.100° C.40°或140° D.40或100°
8.如图,点P为⊙O外一点,过点P作⊙O的切线PA、PB,记切点为A、B,点C为⊙O上一点,连接AC、BC.若∠ACB=62°,则∠APB等于( )
A.68° B.64° C.58° D.56°
9.如图,正六边形ABCDEF内接于⊙O,⊙O的半径为6,则这个正六边形的边心距OM和BC的长分别为( )
A.,π B.,π C., D.,2π
10.某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图所示,已知矩形的宽为,高为,则改建后门洞的圆弧长是( ).
A. B. C. D.
二、填空题
11.如图,AB 是⊙O的直轻,点C是半径OA的中点.过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA的度数是
12. 如图,是的内接三角形,是的直径,,的平分线交于点,则的度数是 .
13.如图,⊙O是△ABC的外接圆,BC是⊙O的直径,AB=AC.∠ABC的平分线交AC于点D,交⊙O于点E,连结CE.若CE= ,则BD的长为
14.如图,分别以正方形ABCD的顶点A,B为圆心,AB长为半径作弧,两弧交于点E.若的长为,则正方形的边长为
三、解答题
15.如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P.若∠P=30°,∠ABC=100°,求∠C的度数.
16.如图,⊙O的直径AB和弦CD相交于点E.已知AE=1,EB=5,∠DEB=60°,求CD 的长.
17.如图,在两个同心圆O中,、都是大圆的弦,且,与小圆相切于点D,则与小圆相切吗?请说明理由.
18.如图,以正六边形ABCDEF的边AB为边,在正六边形内作正方形ABMN,连结MC.求∠BCM的度数.
四、综合题
19.如图,为的直径,点在上,延长至点,使.延长与的另一个交点为,连结.
(1)求证:;
(2)若,求的长.
20.如图,与等边的边、分别交于点、,是的直径,过点作于点.
(1)求证:是的切线:
(2)已知的半径为3,连接,当等边的边长为多少时,与相切?
21.如图,圆中延长弦,交于点,连接,,,.
(1)若,,求的度数;
(2)若,,,判断,,满足什么数量关系时,?请说明理由.
22.如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,点E是BC的中点,连结并延长OE交圆于点D.
(1)求证:ODAC.
(2)若DE=2,BE=2,求阴影部分的面积.
答案解析部分
1.【答案】C
【解析】【解答】解:如图可知,∠ACB和∠AOB在同一圆中,且所对的弧均为弧AB. 根据圆周角定理可知,∠AOB=2∠ACB=2×48°=96°.
故答案为:C.
【分析】根据圆周角定理可知,在同一圆中,同弧所对的圆周角等于圆心角的一半.
2.【答案】C
【解析】【解答】解:∵AB是⊙O的直径,弦CD⊥AB于点E,
∴
在中,
∴.
故答案为:C.
【分析】根据垂径定理求出CE的长,结合勾股定理即可得到OE的长,最后根据线段间的数量关系即可求解.
3.【答案】C
【解析】【解答】解: A、不在一条直线上的三点确定一个圆 ,故不符合题意;
B、 能够互相重合的弧叫做等弧,故不符合题意;
C、 90°的圆周角所对的弦是直径 ,故符合题意;
D、 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,故不符合题意.
故答案为:C.
【分析】根据确定圆的条件,圆周角定理、弧弦圆心角的关系、等弧的定义逐项判断即可.
4.【答案】B
【解析】【解答】解:∵ ⊙O的半径是6,点A到圆心O的距离是5 ,
∴A到圆心O的距离小于⊙O的半径,
∴点A在⊙O内 ,
故答案为:B.
【分析】设⊙O的半径为r,点到圆心O的距离为d,当d<r时,点在圆内;当d=r时,点在圆上,当d>r时,点在圆外,据此判断即可.
5.【答案】C
【解析】【解答】解:∵四边形ABCO是平行四边形,
∴∠AOC=∠ABC,
∵四边形ABCD是圆的内接四边形,
∴∠ADC+∠ABC=180°,
而∠ADC=∠AOC,
∴2∠ADC+∠ADC=180°,解得:∠ADC=60°.
故答案为:C.
【分析】由平行四边形的对角相等可得∠AOC=∠ABC,由圆圆内接四边形的对角互补可得∠ADC+∠ABC=180°然后根据圆周角定理可得关于∠ADC的方程,解方程可求解.
6.【答案】B
【解析】【解答】∵半径,所对应圆心角的度数为,
∴,
∴∠AOC=∠BOC=70°,
∵,
∴∠ADC=∠AOC=35°,
故答案为:B.
【分析】先利用垂径定理可得,再利用圆周角的性质可得∠ADC=∠AOC=35°.
7.【答案】C
【解析】【解答】解:分两种情况,
①△ABC为锐角三角形时,
∵
∴
②△ABC为钝角三角形,
在优弧BC上任取一点P,连接BP,CP,
∵
∴
∴
综上所述,∠BAC的度数为:40°,140°,
故答案为:C.
【分析】根据题意可知需分两种情况讨论:①△ABC为锐角三角形,②△ABC为钝角三角形,分别根据圆周角定理和圆内接四边形的性质,即可求解.
8.【答案】D
【解析】【解答】解:∵ 圆周角∠ACB=62°
∴(圆周角的度数等于它所对弧上的圆心角度数的一半)
∴
∵PA、PB是⊙O的切线 ,
∴
∴P、A、B、O四点共圆(四边形对角互补,那么四点共圆)
∴(圆的内接四边形对角和是180度)
∴
故答案为:D
【分析】圆周角的度数等于它所对弧上的圆心角度数的一半,这是圆周角定理;圆的内接四边形对角和是180度,反过来四边形对角和是180°那么四点共圆,这两个定理都是有关圆的角度证明时经常用到的。
9.【答案】D
10.【答案】C
【解析】【解答】解:如图,矩形内接于,连接、,
四边形是矩形,
,
为的直径,
,,
,,
,
,
.
故答案为:.
【分析】先利用矩形的性质和圆周角定理证得AC是直径,再通过直角三角形的性质得到的度数,从而求得的度数,接着利用弧长的计算公式求得改建后门洞的圆弧长.
11.【答案】30°
【解析】【解答】解:∵ 点C是半径OA的中点.DE⊥AB ,
∴OD=2OC,∠DCO=90°,
∴∠D=30°,
∴∠AOD=90°-30°=60°,
∴ ∠DFA =∠AOD=30°,
故答案为:30°,
【分析】由题意得OD=2OC,利用直角三角形的性质可得∠D=30°,从而求出∠AOD=60°,再根据圆周角定理求解即可.
12.【答案】
【解析】【解答】解:
∵AC是直径,∴∠ABC=90°,
∵BD平分∠ABC,∴∠ABD=45°,
又∵∠D=∠C=50°
∴∠BAD=180°-∠ABD-∠D=180°-45°-50°=85°。
故答案为:85°
【分析】直径所对的圆周角是90°,同弧所对的圆周角相等,由此可得出∠ABC和∠D的度数,再根据内角和定理求出∠BAD。
13.【答案】
【解析】【解答】解:如图,延长BA,CE,交于点M.
∵BC是⊙O的直径,
∴∠BAD=∠CAM=90°,∠BEC=∠BEM=90°,
又AB=AC,∠ABD=∠ACM,
∴△ABD≌△ACM,
∴BD=CM.
由∠EBM=∠EBC,BE= BE,∠BEC=∠BEM,得△BEC≌△BEM,
∴EC=EM,
∴BD=CM=2CE=.
【分析】延长BA,CE,交于点M,证明△ABD≌△ACM(ASA),可得BD=CM.再证△BEC≌△BEM(ASA),可得EC=EM,根据BD=CM=2CE即可求解.
14.【答案】4
15.【答案】解:∵四边形ABCD为圆的内接四边形,
∴∠D+∠ABC=180°,
∵∠ABC=100°,∴∠D=180°-100°=80°,
∵∠P=30°,
∴∠C=180°-30°-80°=70°.
【解析】【分析】根据圆内接四边形的性质可求出∠D的度数,然后在三角形PCD中,用三角形内角和定理可求解.
16.【答案】解:作OF⊥CD于点F ,连结OD,
AB=AE+ BE =6,即⊙O的半径为3.
在Rt△OEF中,OE=OA-AE=3-1=2,∠DEB=60° ,则∠EOF=30° ,OF= ,
在Rt△ODF中,DF= ,
∴CD=2DF= .
【解析】【分析】作OF⊥CD于点F , 连结OD, 先求出 ⊙O 的半径,再根据勾股定理求出OF和DF的长,最后利用垂径定理求出CD的长.
17.【答案】解:过点O作于E,设小圆与的切点为D,连接,如图,
由切线性质可知,
由垂径定理可知,
∵,
∴,
在和中,,
∴,
∴,
∴与小圆相切.
【解析】【分析】 过点O作OE⊥AC于E,设小圆与AB的切点为D,连接OD、OA,由切线性质可知OD⊥AB, 由垂径定理可知AD=DB,AE=EC,结合AB=AC可得AD=AE,利用HL证明Rt△ AEO≌Rt△ADO,得到OE=OD,据此证明.
18.【答案】解:∵六边形ABCDEF为正六边形,
∴∠ABC=120°,AB=BC.
∵四边形ABMN为正方形,
∴∠ABM=90° ,AB= BM.
∴∠MBC=120°-90°=30,BM=BC.
∴∠BCM=∠BMC=×(180°-30°)=75°.
【解析】【分析】利用正六边形的性质,可证得∠ABC=120°,AB=BC,利用正方形的性质可推出∠ABM=90° ,AB= BM;再求出∠MBC的度数,同时可证得BM=BC,然后利用等腰三角形的性质和三角形的内角和定理求出∠BCM的度数.
19.【答案】(1)证明:为的直径,
,
,
,
在和中,
,
,
,
,
;
(2)解:设,
,
,
在中,由勾股定理可得,
即,
解得:,(舍去),
,
由(1)得:,
,
,
,
的长为.
【解析】【分析】(1)由圆周角定理可得∠ACB=90°,则∠ACD=180°-∠ACB=90°,由已知条件可知DC=BC,AC=AC,利用SAS证明△ACD≌△ACB,得到∠D=∠B,由圆周角定理可得∠B=∠E,据此证明;
(2)设BC=x,则AC=x-2,在Rt△ABC中,根据勾股定理可得x的值,由(1)得∠D=∠E,则CD=CE,结合DC=CB可得CE=CB,据此解答.
20.【答案】(1)证明:∵ 是等边三角形,
∴ ,
∵ ,
∴ 是等边三角形,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
又∵ 为 的半径,
∴ 是 的切线
(2)解:∵ 都是 的切线,
∴ ,
∵ 是等边三角形,
∴ ,
∴ ,
∴ ,
∴ ,
由(1)得 是等边三角形,
∴ ,
在 中, ,则 ,
∴ ,
∴ ,
∴当等边 的边长为9时, 与 相切.
【解析】【分析】(1)先证明,再结合OD是的半径,可得DF是的切线;
(2)根据切线的性质可得,再利用“AAS”证出,可得,再结合,证出 是等边三角形,最后求出即可。
21.【答案】(1)解:∵,,
∴∠ACB=∠ADB=60°,∠BCD=∠BAD=10°,
∴∠ACD=∠ACB+∠BCD=60°+10°=70°
(2)解:当γ=2(α+β)时,AD=CD,
∵,,
∴∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,
∴∠ACD=∠ACB+∠BCD=α°+β°,
∵AD=CD,
∴∠ACD=∠DAC,
∵,
∴∠CAD=∠CBD=∠ACD,
∵∠DBA+∠ACD=180°,∠EBD+∠DBA=180°,
∴∠ACD=∠EBD,
∴∠EBC=∠EBD+∠DBC=2∠ACD=γ°,
∴γ=2(α+β)
【解析】【分析】(1)利用同弧所对的圆周角相等,可求出∠ACB,∠BCD的度数,再根据∠ACD=∠ACB+∠BCD,代入计算求出∠ACD的度数.
(2)利用同弧所对的圆周角相等,可证得∠ACB=∠ADB=α°,∠BAD=∠BCD=β°,可得到∠ACD=α°+β°,利用等边对等角可证得∠ACD=∠DAC,再利用圆周角定理可得到∠CAD=∠CBD=∠ACD,利用圆内接四边形的性质可得到∠ACD=∠EBD,由此可推出∠EBC=2∠ACD,即可证得结论.
22.【答案】(1)证明:如图连接OC,
∵OC=OB,点E为BC的中点,
∴OE⊥BC,
∴∠BEO=90°,
∵AB为圆的直径,
∴∠ACB=∠BEO=90°,
∴OD∥AC;
(2)解:连接OC,设圆的半径为r,则OE=r-2,
∵,
∴,
解得,
∴,
∴∠ABC=30°,
∴∠COA=60°,
由(1)可得,
∴,
∴,
∵△BOC与△AOC等底同高,
∴,
∴.
【解析】【分析】(1)连接OC,由等腰三角形的性质可得OE⊥BC,由AB为圆的直径,可得∠ACB=∠BEO=90°,根据平行线的判定即证;(2)连接OC,设圆的半径为r,则OE=r-2,由勾股定理知,据此建立关于r方程,求出r=4,由线段的中点可得OE=2,从而得出∠ABC=30°,继而得出∠COA=60°, 由(1)可得, 利用垂径定理可得,求出, 根据三角形等底同高可得, 根据,利用扇形的面积公式即可求解.
同课章节目录
