解决问题易错真题汇编:多边形的面积(拔高卷)数学五年级上册人教版(含解析)
文档属性
| 名称 | 解决问题易错真题汇编:多边形的面积(拔高卷)数学五年级上册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 12:01:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
解决问题易错真题汇编:多边形的面积(拔高卷)数学五年级上册人教版
1.(2022秋·广西玉林·五年级统考期末)用48米的长的篱笆,在靠墙的地方围一块菜地,(如图)这块菜地的面积是多少平方米?如果照每平方米地一年能收入5.8元计算,这块菜地一年能收入多少元?
2.(2022秋·广东江门·五年级统考期末)一块平行四边形的菜地,它的底是12.5米,高是12米,这块菜地的面积是多少平方米?
3.(2022秋·五年级课时练习)学校里有一个梯形花坛,它的面积是30平方米。它的下底是8.5米,高是4米,上底是多少米?
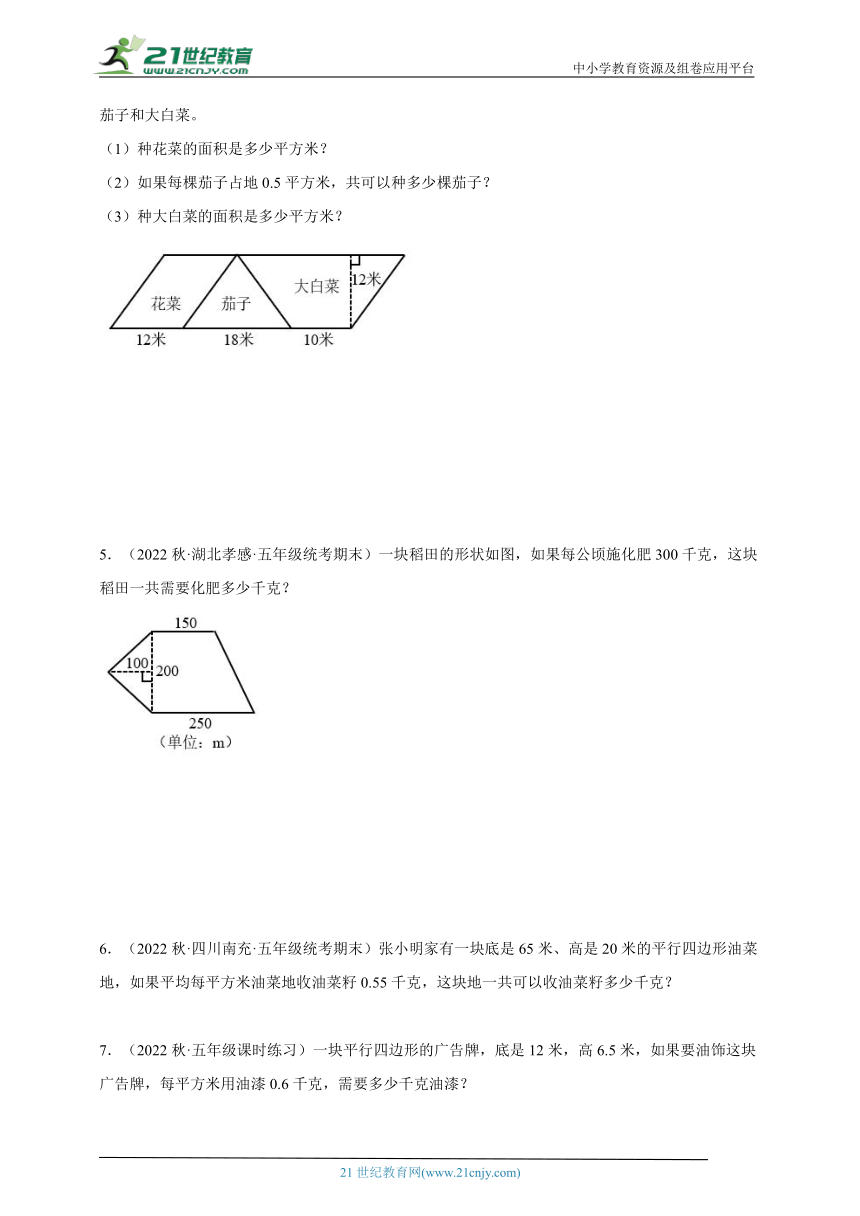
4.(2022秋·长沙·五年级专题练习)有一块平行四边形地,分成3块种蔬菜(如图),分别种花菜、茄子和大白菜。
(1)种花菜的面积是多少平方米?
(2)如果每棵茄子占地0.5平方米,共可以种多少棵茄子?
(3)种大白菜的面积是多少平方米?
5.(2022秋·湖北孝感·五年级统考期末)一块稻田的形状如图,如果每公顷施化肥300千克,这块稻田一共需要化肥多少千克?
6.(2022秋·四川南充·五年级统考期末)张小明家有一块底是65米、高是20米的平行四边形油菜地,如果平均每平方米油菜地收油菜籽0.55千克,这块地一共可以收油菜籽多少千克?
7.(2022秋·五年级课时练习)一块平行四边形的广告牌,底是12米,高6.5米,如果要油饰这块广告牌,每平方米用油漆0.6千克,需要多少千克油漆?
8.(2022秋·五年级课时练习)一个梯形,上底24厘米,下底36厘米,高15厘米。这个梯形的面积是多少平方厘米?
9.(2022秋·五年级课时练习)如图,有一块平行四边形稻田,一条宽2米的小路从中穿过,实际种水稻的面积是多少?
10.(2022秋·五年级课时练习)王师傅给一块长36米、高4米的平行四边形广场地面铺设地砖,升级改造。他平均每天铺设了40平方米的地砖,用了几天完成任务?
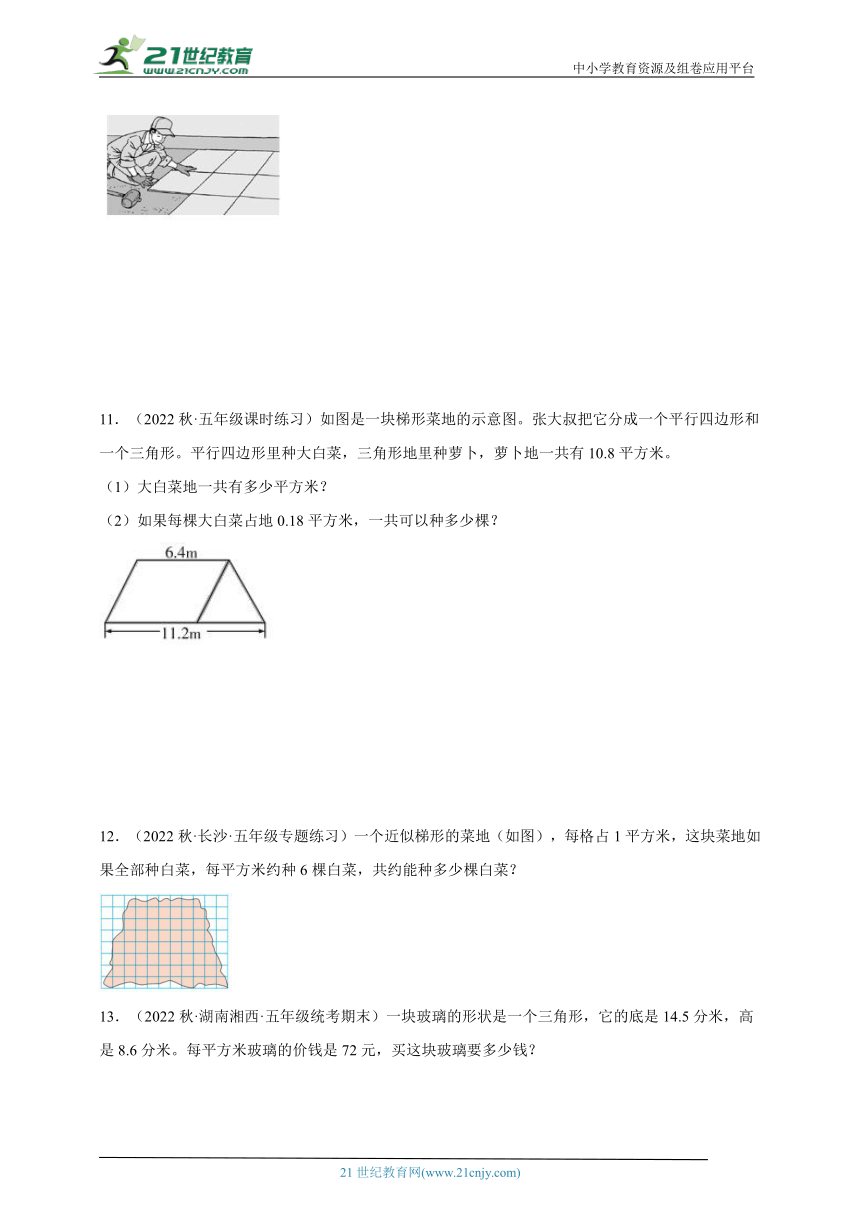
11.(2022秋·五年级课时练习)如图是一块梯形菜地的示意图。张大叔把它分成一个平行四边形和一个三角形。平行四边形里种大白菜,三角形地里种萝卜,萝卜地一共有10.8平方米。
(1)大白菜地一共有多少平方米?
(2)如果每棵大白菜占地0.18平方米,一共可以种多少棵?
12.(2022秋·长沙·五年级专题练习)一个近似梯形的菜地(如图),每格占1平方米,这块菜地如果全部种白菜,每平方米约种6棵白菜,共约能种多少棵白菜?
13.(2022秋·湖南湘西·五年级统考期末)一块玻璃的形状是一个三角形,它的底是14.5分米,高是8.6分米。每平方米玻璃的价钱是72元,买这块玻璃要多少钱?
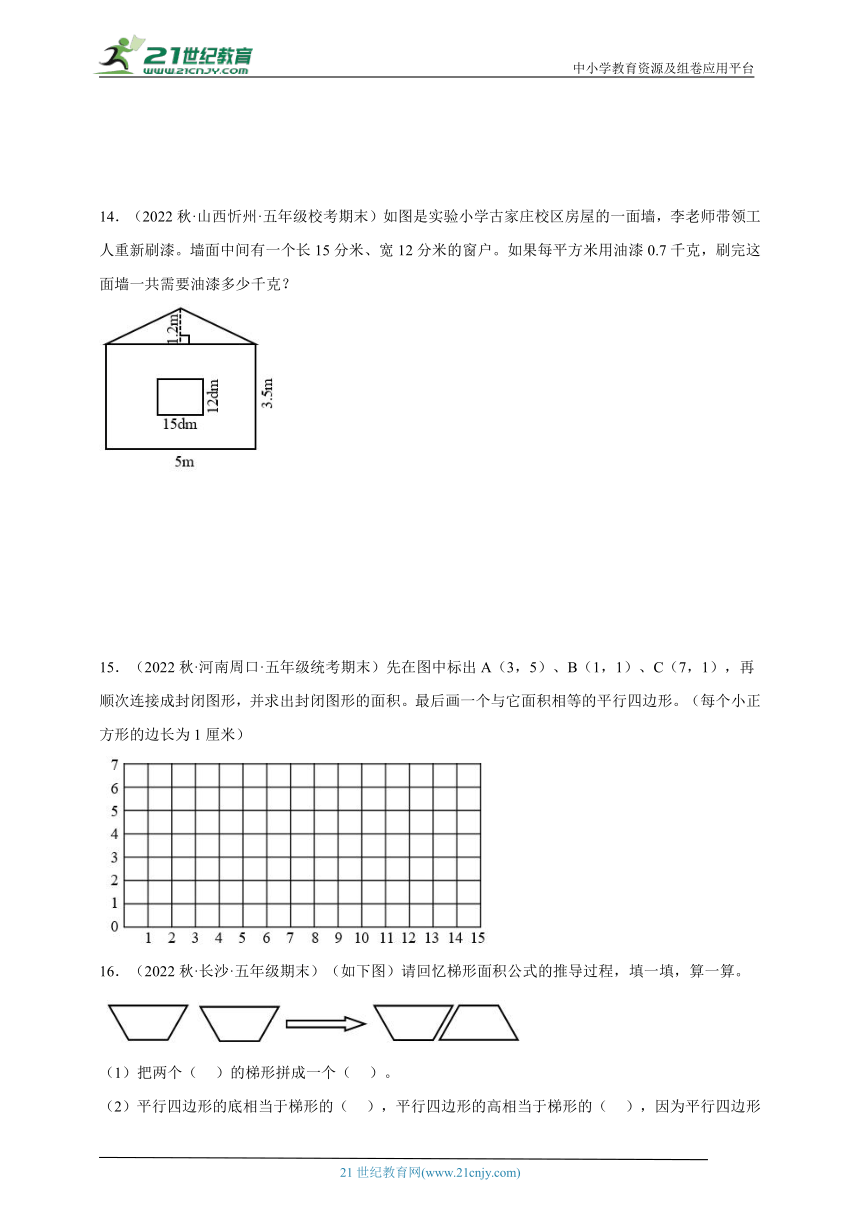
14.(2022秋·山西忻州·五年级校考期末)如图是实验小学古家庄校区房屋的一面墙,李老师带领工人重新刷漆。墙面中间有一个长15分米、宽12分米的窗户。如果每平方米用油漆0.7千克,刷完这面墙一共需要油漆多少千克?
15.(2022秋·河南周口·五年级统考期末)先在图中标出A(3,5)、B(1,1)、C(7,1),再顺次连接成封闭图形,并求出封闭图形的面积。最后画一个与它面积相等的平行四边形。(每个小正方形的边长为1厘米)
16.(2022秋·长沙·五年级期末)(如下图)请回忆梯形面积公式的推导过程,填一填,算一算。
(1)把两个( )的梯形拼成一个( )。
(2)平行四边形的底相当于梯形的( ),平行四边形的高相当于梯形的( ),因为平行四边形的面积=( ),所以梯形的面积=( )。
(3)计算上面其中一个梯形的面积。(先动手在图中量出计算时需要的数据,再算出它的面积)
17.(2022秋·浙江宁波·五年级统考期末)王伯伯有一个甲鱼池(如图),每平方米放养甲鱼苗20只,这个甲鱼池可以放养甲鱼苗多少只?
18.(2022秋·甘肃陇南·五年级校考期末)有一块梯形田地,上底长75米,下底和高都是120米。如果每株玉米平均占地0.16平方米,那么这块田地可以种多少株玉米?
19.(2022秋·新疆阿克苏·五年级校考期末)一个梯形果园,上底长18米,比下底短5米,高16米。现在在这个果园里栽上梨树,每棵梨树占地4平方米。
(1)这个果园的面积多少平方米?
(2)这个果园可以栽多少棵梨树?
20.(2022秋·山西阳泉·五年级统考期末)探索梯形奥秘。
(1)如图,这个梯形的面积是多少?
(2)如果把这个梯形的上底增加1厘米、下底减少1厘米,得到的新梯形的面积是多少?与原梯形的面积之间有什么关系?
(3)请你判断:如果梯形的上底增加2厘米、下底减少2厘米呢?得到的新梯形面积与原梯形的面积之间有什么关系?
(4)你发现了什么?尝试说明理由。
21.(2022秋·浙江金华·五年级统考期末)小区有一块直角三角形的绿地,这块绿地里有一条小路(如图中虚线所示)。请你用学过的知识,帮忙算出这条小路有多长?
22.(2021秋·海南省直辖县级单位·五年级统考期末)一个三角形的底是2.5分米,高是底的2倍,求这个三角形的面积。
23.(2021秋·河南洛阳·五年级统考期末)一个梯形,如果上底增加6.4厘米,就变成一个平行四边形,如果上底减少5.8厘米,就变成一个三角形,此时面积就减少了21.46平方厘米,原来的梯形的面积是多少平方厘米?
24.(2021秋·河南洛阳·五年级统考期末)一个等边三角形的周长是27厘米,高是3.6厘米,它的面积是多少平方厘米?
25.(2022秋·河南洛阳·五年级统考期中)为了便于给花草浇水、施肥,苗圃管理员在苗圃地里留下两条小路,一条是长方形,一条是平行四边形的,这样,可种植花草部分的面积是多少?(如图,单位:米)
26.(2022秋·福建宁德·五年级统考期中)有一个三角形的底是6米,如果底延长2米,面积就增加4平方米。原来三角形的面积是多少平方米?
27.(2022春·贵州六盘水·五年级统考期末)据中国载人航天工程办公室消息,北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆。玲玲为庆祝神舟十三号载人飞行任务取得圆满成功,画了一幅正六边形的神舟十三号飞船标识图(如图所示),这幅图的面积是多少?
28.(2022秋·重庆綦江·五年级统考期末)沙漏是古代计量时间的工具之一。一种沙漏的截面是一个轴对称图形(如图),你能计算出这个沙漏截面的面积吗?(单位:厘米)
29.(2021秋·重庆黔江·五年级统考期末)公路旁有一块三角形的空地(如图),要在这空地上种上草坪,8万元钱够不够?
30.(2022秋·广东江门·五年级统考期末)李大爷家有一块平行四边形的小花园,他想用篱笆围起来。
(1)李大爷家的小花园需要( )米篱笆。
(2)如果两个公司所售的篱笆质量相同,请你帮张大爷算一算,选用哪家公司的比较合算?
(3)这个花园的面积是多少平方米?
参考答案:
1.288平方米;1670.4元
【分析】观察图形,用篱笆围成的菜地是一个直角梯形,且有一面靠墙,梯形的高是24米;因为梯形的上底+下底+高=篱笆的长度,所以用篱笆的长度减去24,即是梯形上底与下底的和;
根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可求出这块菜地的面积;
最后用这块菜地的面积乘每平方米地一年的收入,即是这块菜地一年的总收入。
【详解】(48-24)×24÷2
=24×24÷2
=576÷2
=288(平方米)
288×5.8=1670.4(元)
答:这块菜地的面积是288平方米,这块菜地一年能收入1670.4元。
【点睛】本题考查梯形面积公式的灵活运用,求出梯形的上底与下底之和是解题的关键。
2.150平方米
【分析】平行四边形的面积=底×高,把题中数据代入公式计算即可。
【详解】12.5×12=150(平方米)
答:这块菜地的面积是150平方米。
【点睛】本题主要考查平行四边形面积公式的应用,熟记公式是解答题目的关键。
3.6.5米
【分析】根据梯形的面积公式:S=(a+b)h÷2,用30乘2除以4,再减去8.5即可求出上底是多少。
【详解】30×2÷4-8.5
=60÷4-8.5
=15-8.5
=6.5(米)
答:上底是6.5米。
【点睛】本题考查梯形的面积,灵活运用梯形的面积公式是解题的关键。
4.(1)144平方米
(2)216棵
(3)228平方米
【分析】(1)种花菜的土地是平行四边形,根据平行四边形面积=底×高,进行解答。
(2)种茄子的土地是三角形,根据三角形面积=底×高÷2,求出三角形面积,用总面积÷每棵茄子面积=茄子数量。
(3)种大白菜的土地可以看作是一个梯形,梯形上底为(18+10)米,下底为10米,高为12米,根据梯形面积=(上底+下底)×高÷2,进行解答。
【详解】(1)12×12=144(平方米)
答:种花菜的面积是144平方米。
(2)18×12÷2÷0.5=216(棵)
答:共可以种216棵茄子
(3)(10+18+10)×12÷2
=38×12÷2
=228(平方米)
答:种大白菜的面积是228平方米。
【点睛】掌握不同图形的面积公式是解答此题的关键。
5.1500千克
【分析】观察图形可知,稻田由一个底为200米、高为100米的三角形和一个上底为150米、下底为250米、高为200米的梯形组成,根据三角形的面积公式和梯形的面积公式求解即可,然后根据1公顷=10000平方米,将单位换算成公顷,然后再乘300即可求出这块稻田一共需要化肥多少千克。
【详解】200×100÷2+(150+250)×200÷2
=10000+400×100
=10000+40000
=50000(平方米)
50000平方米=5公顷
5×300=1500(千克)
答:这块稻田一共需要化肥1500千克。
【点睛】本题主要考查了三角形面积公式和梯形面积公式的灵活应用。
6.715千克
【分析】先根据平行四边形的面积=底×高,求出这块油菜地的面积,再乘每平方米油菜地收收油菜籽的质量,即是这块地一共可以收油菜籽的总质量。
【详解】65×20=1300(平方米)
0.55×1300=715(千克)
答:这块地一共可以收油菜籽715千克。
【点睛】本题考查平行四边形面积公式、小数乘法的意义及应用。
7.46.8千克
【分析】根据平行四边形的面积公式:S=ab,据此求出广告牌的面积,再用广告牌的面积乘每平方米用油漆的重量即可求解。
【详解】12×6.5×0.6
=78×0.6
=46.8(千克)
答:需要46.8千克油漆。
【点睛】本题考查小数乘法,结合平行四边形的面积公式是解题的关键。
8.450平方厘米
【分析】梯形面积=(上底+下底)×高÷2,把数据代入公式求解即可。
【详解】(24+36)×15÷2
=60×15÷2
=900÷2
=450(平方厘米)
答:这个梯形的面积是450平方厘米。
【点睛】掌握梯形面积公式是解决此题的关键。
9.380平方米
【分析】如图:把这个组合经过平移后,实际种水稻的面积相当于一个底为(22-2)米,高为19米的平行四边形,利用平行四边形的面积=底×高,代入数据,即可求出实际种水稻的面积是多少。
【详解】(22-2)×19
=20×19
=380(平方米)
答:实际种水稻的面积是380平方米。
【点睛】此题的解题关键是巧妙的通过平移图形,利用平行四边形的面积公式,求出组合图形的面积。
10.3.6天
【分析】先根据平行四边形的面积=底×高,求出广场地面的面积,然后除以每天铺设地砖的面积,即可求出完成任务需要的天数。
【详解】36×4=144(平方米)
144÷40=3.6(天)
答:用了3.6天完成任务。
【点睛】本题考查平行四边形的面积公式的运用、小数除法的计算是解题的关键。
11.(1)28.8平方米
(2)160棵
【分析】(1)由题意可知,平行四边形的高就是三角形的高,根据三角形的面积公式:S=ab÷2,据此求出三角形的高,再根据平行四边形的面积公式:S=ab,据此代入数值进行计算即可求出白菜地的面积;
(2)用平行四边形的面积除以0.18即可求出共可以种多少棵。
【详解】(1)10.8×2÷(11.2-6.4)
=21.6÷4.8
=4.5(米)
6.4×4.5=28.8(平方米)
答:大白菜地一共有28.8平方米。
(2)28.8÷0.18=160(棵)
答:一共可以种160棵。
【点睛】本题考查平行四边形和三角形的面积,熟记公式是解题的关键。
12.432棵
【分析】每格占1平方米,则小方格的边长为1米,把这块菜地看作一个梯形,梯形的上底是7米,下底是11米,高是8米,利用“梯形的面积=(上底+下底)×高÷2”求出这块菜地的面积,一共种白菜的数量=这块地的面积×每平方米种白菜的数量,据此解答。
【详解】
(7+11)×8÷2×6
=18×8÷2×6
=144÷2×6
=72×6
=432(棵)
答:共约能种432棵白菜。
【点睛】掌握梯形的面积计算公式是解答题目的关键。
13.44.89元
【分析】先根据“三角形的面积=底×高÷2”求出这块三角形玻璃的面积;再根据“单价×数量=总价”求出买这块玻璃的钱数。
【详解】14.5分米=1.45米
8.6分米=0.86米
1.45×0.86÷2×72
=1.247÷2×72
=0.6235×72
=44.892(元)
≈44.89(元)
答:买这块玻璃约要44.89元。
【点睛】明确三角形的面积计算公式是解决此题的关键。
14.13.09千克
【分析】从图中可知,墙面需刷漆的面积=三角形的面积+大长方形的面积-小长方形的面积(即窗户的面积),根据三角形的面积=底×高÷2,长方形的面积=长×宽,分别代入数据计算求出墙面需刷漆的面积,再乘每平方米用油漆的质量即可;注意单位的换算:1米=10分米。
【详解】15分米=1.5米
12分米=1.2米
三角形的面积:
5×1.2÷2
=6÷2
=3(平方米)
大长方形的面积:
5×3.5=17.5(平方米)
小长方形的面积(窗户的面积):
1.5×1.2=1.8(平方米)
墙面需刷漆的面积:
3+17.5-1.8
=20.5-1.8
=18.7(平方米)
一共需要油漆:
0.7×18.7=13.09(千克)
答:刷完这面墙一共需要油漆13.09千克。
【点睛】本题考查三角形、长方形面积公式的运用,关键是弄清组合图形的面积是由哪些学过的规则图形的面积相加或相减得到,再运用相关的图形面积公式列式计算。
15.见详解;6平方厘米;见详解
【分析】根据数对表示位置的方法,数对的第一个数字表示列,第二个数字表示行;据此在图中找到A、B、C三个点的位置,再顺次连接成封闭图形,得到一个三角形;根据三角形的面积=底×高÷2,求出这个封闭图形的面积;
要画一个与封闭图形面积相等的平行四边形,根据平行四边形的面积=底×高,确定平行四边形的底和高,即可画出这个平行四边形。
【详解】封闭图形的面积:
6×4÷2
=24÷2
=12(平方厘米)
因为12=6×2,所以可以画一个底是6厘米、高是2厘米的平行四边形。
如图:
(平行四边形的画法不唯一)
【点睛】本题考查根据数对找位置以及三角形、平行四边形面积公式的运用,画平行四边形时,只需保证平行四边形的面积是12平方厘米,形状不唯一。
16.(1)形状相同;平行四边形;
(2)上底与下底的和;高;底×高;(上底+下底)×高÷2;
(3)测量数据见详解;1.125平方厘米
【分析】两个形状相同的梯形可以拼成一个平行四边形,平行四边形的面积等于梯形面积的2倍,由图可知,梯形的上底与下底的和相当于平行四边形的底,梯形的高相当于平行四边形的高,平行四边形的面积=底×高=(上底+下底)×高=梯形的面积×2,所以梯形的面积=平行四边形的面积÷2=(上底+下底)×高÷2,最后测量其中一个梯形的上底、下底、高,再把数据代入公式求出这个梯形的面积,据此解答。
【详解】(1)把两个形状相同的梯形拼成一个平行四边形。
(2)平行四边形的底相当于梯形的上底与下底的和,平行四边形的高相当于梯形的高,因为平行四边形的面积=底×高,所以梯形的面积=(上底+下底)×高÷2。
(3)
(1+2)×0.75÷2
=3×0.75÷2
=2.25÷2
=1.125(平方厘米)
答:这个梯形的面积是1.125平方厘米。
【点睛】掌握梯形面积计算公式的推导过程是解答题目的关键。
17.119000只
【分析】观察图形可知,甲鱼池由一个上底为30米、下底为80米、高为(90-40)米的直角梯形和一个长为80米、宽为40米的长方形组成,根据梯形的面积公式和长方形的面积公式求解即可得到甲鱼池的面积,已知每平方米放养甲鱼苗20只,则用甲鱼池的面积乘20即可求出放养甲鱼苗的总只数。
【详解】90-40=50(米)
(30+80)×50÷2
=110×50÷2
=5500÷2
=2750(平方米)
80×40=3200(平方米)
2750+3200=5950(平方米)
5950×20=119000(只)
答:这个甲鱼池可以放养甲鱼苗119000只。
【点睛】本题主要考查了梯形面积和长方形面积的灵活应用。
18.73125株
【分析】根据“梯形的面积=(上底+下底)×高÷2”求出这块地的面积,这块地可以种玉米的株数=这块地的面积÷每株玉米的占地面积,据此解答。
【详解】(75+120)×120÷2÷0.16
=195×120÷2÷0.16
=23400÷2÷0.16
=11700÷0.16
=73125(株)
答:这块田地可以种73125株玉米。
【点睛】本题主要考查梯形面积公式的应用,熟记公式是解答题目的关键。
19.(1)328平方米;
(2)82棵
【分析】(1)下底=上底+5米,求出下底,再根据梯形的面积=(上底+下底)×高÷2,代入数据,即可求出果园的面积。
(2)用果园的面积除以每棵梨树占地的面积,即可求出这个果园可以栽多少棵梨树。
【详解】(1)18+5=23(米)
(18+23)×16÷2
=41×16÷2
=328(平方米)
答:这个果园的面积是328平方米。
(2)328÷4=82(棵)
答:这个果园可以栽82棵梨树。
【点睛】此题的解题关键是灵活运用梯形的面积公式求解。
20.(1)32.5平方厘米
(2)32.5平方厘米;与原梯形的面积相等
(3)32.5平方厘米;与原梯形的面积相等
(4)如果把梯形的上底增加a厘米、下底减少a厘米,得到的新梯形的面积不变。因为梯形的上、下底之和不变,高不变,梯形的面积就不变
【分析】(1)梯形面积=(上底+下底)×高÷2,将数据代入公式,求出这个梯形的面积;
(2)将上底加1厘米,下底减去1厘米,求出变化后的上底和下底,再根据梯形的面积公式求出新梯形的面积,从而判断它和原来梯形的面积关系;
(3)将上底加2厘米,下底减去2厘米,求出变化后的上底和下底,再根据梯形的面积公式求出新梯形的面积,从而判断它和原来梯形的面积关系;
(4)根据(2)和(3),发现上、下底之和不变,高不变,梯形的面积就不变。
【详解】(1)(4+9)×5÷2
=13×5÷2
=65÷2
=32.5(平方厘米)
答:这个梯形的面积是32.5平方厘米。
(2)4+1=5(厘米)
9-1=8(厘米)
(5+8)×5÷2
=13×5÷2
=65÷2
=32.5(平方厘米)
答:新梯形的面积是32.5平方厘米,与原梯形的面积相等。
(3)4+2=6(厘米)
9-2=7(厘米)
(6+7)×5÷2
=13×5÷2
=65÷2
=32.5(平方厘米)
答:新梯形的面积是32.5平方厘米,与原梯形的面积相等。
(4)答:我发现如果把梯形的上底增加a厘米、下底减少a厘米,得到的新梯形的面积不变。因为梯形的上、下底之和不变,高不变,梯形的面积就不变。
【点睛】本题考查了梯形的面积,解题关键是熟记梯形的面积公式。
21.24米
【分析】观察图形可知,这条小路的长度就是三角形的高,根据三角形的面积公式:S=ab÷2,用30乘40再除以2,即可求出三角形的面积;然后用三角形的面积乘2,再除以50即可求出三角形的高,也就是小路的长度。
【详解】30×40÷2×2÷50
=1200÷2×2÷50
=600×2÷50
=1200÷50
=24(米)
答:这条小路长为24米。
【点睛】本题考查三角形的面积,灵活运用三角形的面积公式是解题的关键。
22.6.25平方分米
【分析】已知底是2.5分米,高是底的2倍,则高为(2.5×2)分米,然后根据三角形的面积公式求解即可。
【详解】2.5×2=5(分米)
2.5×5÷2
=12.5÷2
=6.25(平方分米)
答:这个三角形的面积6.25平方分米。
【点睛】本题考查了三角形面积公式的灵活应用。
23.66.6平方厘米
【分析】由题意可知,如果上底增加6.4厘米,就变成一个平行四边形,如果上底减少5.8厘米,就变成一个三角形,则梯形的下底是(6.4+5.8)厘米,上底是5.8厘米;如果上底减少5.8厘米,就变成一个三角形,此时面积就减少了21.46平方厘米,根据三角形的面积公式:S=ab÷2,据此可求出三角形的高是(21.46×2÷5.8),三角形的高也就是梯形的高,再根据梯形的面积公式:S=(a+b)h÷2,据此进行计算即可。
【详解】21.46×2÷5.8
=42.92÷5.8
=7.4(厘米)
(6.4+5.8+5.8)×7.4÷2
=18×7.4÷2
=133.2÷2
=66.6(平方厘米)
答:原来的梯形的面积是66.6平方厘米。
【点睛】本题考查三角形和梯形的面积,熟记公式是解题的关键。
24.16.2平方厘米
【分析】等边三角形的三条边都相等,用27除以3即可求三角形的一条边长,再根据三角形的面积公式:S=ab÷2,据此代入数值进行计算即可。
【详解】27÷3×3.6÷2
=9×3.6÷2
=32.4÷2
=16.2(平方厘米)
答:它的面积是16.2平方厘米。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
25.456平方米
【分析】观察图形可知,经过平移后,种植花草的部分可拼成一个长为25-1=24米,宽为20-1=19米的长方形,再根据长方形的面积公式:S=ab,据此解答即可。
【详解】(25-1)×(20-1)
=24×19
=456(平方米)
答:可种植花草部分的面积是456平方米。
【点睛】本题考查长方形的面积,结合平移的知识是解题的关键。
26.12平方米
【分析】由“有一个三角形的底是6米,如果底延长2米,面积就增加4平方米”可知,增加部分是一个底2米、高与原来三角形高相等的三角形,根据“三角形面积=底×高÷2”可知,三角形的底=面积×2÷高,求出原三角形的高,再根据三角形面积计算公式求出原来三角形的面积即可。
【详解】4×2÷2
=8÷2
=4(米)
6×4÷2
=24÷2
=12(平方米)
答:原来三角形的面积是12平方米。
【点睛】本题主要考查了三角形面积的计算,注意:增加部分是一个三角形,它的高与等于原来三角形高。
27.259.5cm2
【分析】如图所示,把正六边形分成两个完全一样的梯形,根据“梯形的面积=(上底+下底)×高÷2”求出一个梯形的面积,最后乘2求出正六边形的面积,据此解答。
【详解】
(10+20)×(17.3÷2)÷2×2
=30×8.65÷2×2
=259.5÷2×2
=129.75×2
=259.5(cm2)
答:这幅图的面积是259.5cm2。
【点睛】本题主要考查组合图形面积的计算方法,把组合图形转化为基本图形是解答题目的关键。
28.13.44平方厘米
【分析】观察图形可知,这个沙漏截面的面积=上下两个梯形的面积+中间长方形的面积,因为该沙漏的截面是一个轴对称图形,所以上下两个梯形的高相等,即(6.6-0.6)÷2=3厘米,再根据梯形的面积公式:S=(a+b)h÷2,长方形的面积公式:S=ab,据此计算即可。
【详解】(6.6-0.6)÷2
=6÷2
=3(厘米)
(4+0.4)×3÷2×2
=4.4×3÷2×2
=13.2÷2×2
=13.2(平方厘米)
0.4×0.6=0.24(平方厘米)
13.2+0.24=13.44(平方厘米)
答:这个沙漏截面的面积是13.44平方厘米。
【点睛】本题考查梯形和长方形的面积,熟记公式是解题的关键。
29.够
【分析】根据三角形的面积=底×高÷2,代入数据计算求出这块三角形空地的面积,再乘每平方米草坪的费用,即是要在这块空地上种草坪需要的钱数,最后与8万元作比较,得出结论。
【详解】8万元=80000元
40×26÷2
=1040÷2
=520(平方米)
141×520=73320(元)
73320<80000
答:8万元钱够。
【点睛】掌握三角形的面积公式,以及单价、数量、总价之间的关系是解题的关键。
30.(1)93米;(2)甲公司;(3)405平方米
【分析】(1)根据平行四边形的周长公式:C=(a+b)×2,把数据代入公式求出这个平行四边形的周长,然后减去门的宽就是需要篱笆的长度;
(2)根据单价×数量=总价,求出在甲公司购买需要多少元,然后与乙公司的报价进行比较即可;
(3)根据平行四边形的面积公式:S=ah,把数据代入公式解答。
【详解】(1)(27+20)×2-1
=47×2-1
=94-1
=93(米)
李大爷家的小花园需要93米篱笆。
(2)1.3×93=120.9(元)
120.9元<128.8元
答:选甲公司比较合算。
(3)27×15=405(平方米)
答:这个花园的面积是405平方米。
【点睛】此题主要考查平行四边形的周长公式、面积公式的灵活运用,以及单价、数量、总价三者之间的关系及应用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
解决问题易错真题汇编:多边形的面积(拔高卷)数学五年级上册人教版
1.(2022秋·广西玉林·五年级统考期末)用48米的长的篱笆,在靠墙的地方围一块菜地,(如图)这块菜地的面积是多少平方米?如果照每平方米地一年能收入5.8元计算,这块菜地一年能收入多少元?
2.(2022秋·广东江门·五年级统考期末)一块平行四边形的菜地,它的底是12.5米,高是12米,这块菜地的面积是多少平方米?
3.(2022秋·五年级课时练习)学校里有一个梯形花坛,它的面积是30平方米。它的下底是8.5米,高是4米,上底是多少米?
4.(2022秋·长沙·五年级专题练习)有一块平行四边形地,分成3块种蔬菜(如图),分别种花菜、茄子和大白菜。
(1)种花菜的面积是多少平方米?
(2)如果每棵茄子占地0.5平方米,共可以种多少棵茄子?
(3)种大白菜的面积是多少平方米?
5.(2022秋·湖北孝感·五年级统考期末)一块稻田的形状如图,如果每公顷施化肥300千克,这块稻田一共需要化肥多少千克?
6.(2022秋·四川南充·五年级统考期末)张小明家有一块底是65米、高是20米的平行四边形油菜地,如果平均每平方米油菜地收油菜籽0.55千克,这块地一共可以收油菜籽多少千克?
7.(2022秋·五年级课时练习)一块平行四边形的广告牌,底是12米,高6.5米,如果要油饰这块广告牌,每平方米用油漆0.6千克,需要多少千克油漆?
8.(2022秋·五年级课时练习)一个梯形,上底24厘米,下底36厘米,高15厘米。这个梯形的面积是多少平方厘米?
9.(2022秋·五年级课时练习)如图,有一块平行四边形稻田,一条宽2米的小路从中穿过,实际种水稻的面积是多少?
10.(2022秋·五年级课时练习)王师傅给一块长36米、高4米的平行四边形广场地面铺设地砖,升级改造。他平均每天铺设了40平方米的地砖,用了几天完成任务?
11.(2022秋·五年级课时练习)如图是一块梯形菜地的示意图。张大叔把它分成一个平行四边形和一个三角形。平行四边形里种大白菜,三角形地里种萝卜,萝卜地一共有10.8平方米。
(1)大白菜地一共有多少平方米?
(2)如果每棵大白菜占地0.18平方米,一共可以种多少棵?
12.(2022秋·长沙·五年级专题练习)一个近似梯形的菜地(如图),每格占1平方米,这块菜地如果全部种白菜,每平方米约种6棵白菜,共约能种多少棵白菜?
13.(2022秋·湖南湘西·五年级统考期末)一块玻璃的形状是一个三角形,它的底是14.5分米,高是8.6分米。每平方米玻璃的价钱是72元,买这块玻璃要多少钱?
14.(2022秋·山西忻州·五年级校考期末)如图是实验小学古家庄校区房屋的一面墙,李老师带领工人重新刷漆。墙面中间有一个长15分米、宽12分米的窗户。如果每平方米用油漆0.7千克,刷完这面墙一共需要油漆多少千克?
15.(2022秋·河南周口·五年级统考期末)先在图中标出A(3,5)、B(1,1)、C(7,1),再顺次连接成封闭图形,并求出封闭图形的面积。最后画一个与它面积相等的平行四边形。(每个小正方形的边长为1厘米)
16.(2022秋·长沙·五年级期末)(如下图)请回忆梯形面积公式的推导过程,填一填,算一算。
(1)把两个( )的梯形拼成一个( )。
(2)平行四边形的底相当于梯形的( ),平行四边形的高相当于梯形的( ),因为平行四边形的面积=( ),所以梯形的面积=( )。
(3)计算上面其中一个梯形的面积。(先动手在图中量出计算时需要的数据,再算出它的面积)
17.(2022秋·浙江宁波·五年级统考期末)王伯伯有一个甲鱼池(如图),每平方米放养甲鱼苗20只,这个甲鱼池可以放养甲鱼苗多少只?
18.(2022秋·甘肃陇南·五年级校考期末)有一块梯形田地,上底长75米,下底和高都是120米。如果每株玉米平均占地0.16平方米,那么这块田地可以种多少株玉米?
19.(2022秋·新疆阿克苏·五年级校考期末)一个梯形果园,上底长18米,比下底短5米,高16米。现在在这个果园里栽上梨树,每棵梨树占地4平方米。
(1)这个果园的面积多少平方米?
(2)这个果园可以栽多少棵梨树?
20.(2022秋·山西阳泉·五年级统考期末)探索梯形奥秘。
(1)如图,这个梯形的面积是多少?
(2)如果把这个梯形的上底增加1厘米、下底减少1厘米,得到的新梯形的面积是多少?与原梯形的面积之间有什么关系?
(3)请你判断:如果梯形的上底增加2厘米、下底减少2厘米呢?得到的新梯形面积与原梯形的面积之间有什么关系?
(4)你发现了什么?尝试说明理由。
21.(2022秋·浙江金华·五年级统考期末)小区有一块直角三角形的绿地,这块绿地里有一条小路(如图中虚线所示)。请你用学过的知识,帮忙算出这条小路有多长?
22.(2021秋·海南省直辖县级单位·五年级统考期末)一个三角形的底是2.5分米,高是底的2倍,求这个三角形的面积。
23.(2021秋·河南洛阳·五年级统考期末)一个梯形,如果上底增加6.4厘米,就变成一个平行四边形,如果上底减少5.8厘米,就变成一个三角形,此时面积就减少了21.46平方厘米,原来的梯形的面积是多少平方厘米?
24.(2021秋·河南洛阳·五年级统考期末)一个等边三角形的周长是27厘米,高是3.6厘米,它的面积是多少平方厘米?
25.(2022秋·河南洛阳·五年级统考期中)为了便于给花草浇水、施肥,苗圃管理员在苗圃地里留下两条小路,一条是长方形,一条是平行四边形的,这样,可种植花草部分的面积是多少?(如图,单位:米)
26.(2022秋·福建宁德·五年级统考期中)有一个三角形的底是6米,如果底延长2米,面积就增加4平方米。原来三角形的面积是多少平方米?
27.(2022春·贵州六盘水·五年级统考期末)据中国载人航天工程办公室消息,北京时间2022年4月16日9时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆。玲玲为庆祝神舟十三号载人飞行任务取得圆满成功,画了一幅正六边形的神舟十三号飞船标识图(如图所示),这幅图的面积是多少?
28.(2022秋·重庆綦江·五年级统考期末)沙漏是古代计量时间的工具之一。一种沙漏的截面是一个轴对称图形(如图),你能计算出这个沙漏截面的面积吗?(单位:厘米)
29.(2021秋·重庆黔江·五年级统考期末)公路旁有一块三角形的空地(如图),要在这空地上种上草坪,8万元钱够不够?
30.(2022秋·广东江门·五年级统考期末)李大爷家有一块平行四边形的小花园,他想用篱笆围起来。
(1)李大爷家的小花园需要( )米篱笆。
(2)如果两个公司所售的篱笆质量相同,请你帮张大爷算一算,选用哪家公司的比较合算?
(3)这个花园的面积是多少平方米?
参考答案:
1.288平方米;1670.4元
【分析】观察图形,用篱笆围成的菜地是一个直角梯形,且有一面靠墙,梯形的高是24米;因为梯形的上底+下底+高=篱笆的长度,所以用篱笆的长度减去24,即是梯形上底与下底的和;
根据梯形的面积=(上底+下底)×高÷2,代入数据计算即可求出这块菜地的面积;
最后用这块菜地的面积乘每平方米地一年的收入,即是这块菜地一年的总收入。
【详解】(48-24)×24÷2
=24×24÷2
=576÷2
=288(平方米)
288×5.8=1670.4(元)
答:这块菜地的面积是288平方米,这块菜地一年能收入1670.4元。
【点睛】本题考查梯形面积公式的灵活运用,求出梯形的上底与下底之和是解题的关键。
2.150平方米
【分析】平行四边形的面积=底×高,把题中数据代入公式计算即可。
【详解】12.5×12=150(平方米)
答:这块菜地的面积是150平方米。
【点睛】本题主要考查平行四边形面积公式的应用,熟记公式是解答题目的关键。
3.6.5米
【分析】根据梯形的面积公式:S=(a+b)h÷2,用30乘2除以4,再减去8.5即可求出上底是多少。
【详解】30×2÷4-8.5
=60÷4-8.5
=15-8.5
=6.5(米)
答:上底是6.5米。
【点睛】本题考查梯形的面积,灵活运用梯形的面积公式是解题的关键。
4.(1)144平方米
(2)216棵
(3)228平方米
【分析】(1)种花菜的土地是平行四边形,根据平行四边形面积=底×高,进行解答。
(2)种茄子的土地是三角形,根据三角形面积=底×高÷2,求出三角形面积,用总面积÷每棵茄子面积=茄子数量。
(3)种大白菜的土地可以看作是一个梯形,梯形上底为(18+10)米,下底为10米,高为12米,根据梯形面积=(上底+下底)×高÷2,进行解答。
【详解】(1)12×12=144(平方米)
答:种花菜的面积是144平方米。
(2)18×12÷2÷0.5=216(棵)
答:共可以种216棵茄子
(3)(10+18+10)×12÷2
=38×12÷2
=228(平方米)
答:种大白菜的面积是228平方米。
【点睛】掌握不同图形的面积公式是解答此题的关键。
5.1500千克
【分析】观察图形可知,稻田由一个底为200米、高为100米的三角形和一个上底为150米、下底为250米、高为200米的梯形组成,根据三角形的面积公式和梯形的面积公式求解即可,然后根据1公顷=10000平方米,将单位换算成公顷,然后再乘300即可求出这块稻田一共需要化肥多少千克。
【详解】200×100÷2+(150+250)×200÷2
=10000+400×100
=10000+40000
=50000(平方米)
50000平方米=5公顷
5×300=1500(千克)
答:这块稻田一共需要化肥1500千克。
【点睛】本题主要考查了三角形面积公式和梯形面积公式的灵活应用。
6.715千克
【分析】先根据平行四边形的面积=底×高,求出这块油菜地的面积,再乘每平方米油菜地收收油菜籽的质量,即是这块地一共可以收油菜籽的总质量。
【详解】65×20=1300(平方米)
0.55×1300=715(千克)
答:这块地一共可以收油菜籽715千克。
【点睛】本题考查平行四边形面积公式、小数乘法的意义及应用。
7.46.8千克
【分析】根据平行四边形的面积公式:S=ab,据此求出广告牌的面积,再用广告牌的面积乘每平方米用油漆的重量即可求解。
【详解】12×6.5×0.6
=78×0.6
=46.8(千克)
答:需要46.8千克油漆。
【点睛】本题考查小数乘法,结合平行四边形的面积公式是解题的关键。
8.450平方厘米
【分析】梯形面积=(上底+下底)×高÷2,把数据代入公式求解即可。
【详解】(24+36)×15÷2
=60×15÷2
=900÷2
=450(平方厘米)
答:这个梯形的面积是450平方厘米。
【点睛】掌握梯形面积公式是解决此题的关键。
9.380平方米
【分析】如图:把这个组合经过平移后,实际种水稻的面积相当于一个底为(22-2)米,高为19米的平行四边形,利用平行四边形的面积=底×高,代入数据,即可求出实际种水稻的面积是多少。
【详解】(22-2)×19
=20×19
=380(平方米)
答:实际种水稻的面积是380平方米。
【点睛】此题的解题关键是巧妙的通过平移图形,利用平行四边形的面积公式,求出组合图形的面积。
10.3.6天
【分析】先根据平行四边形的面积=底×高,求出广场地面的面积,然后除以每天铺设地砖的面积,即可求出完成任务需要的天数。
【详解】36×4=144(平方米)
144÷40=3.6(天)
答:用了3.6天完成任务。
【点睛】本题考查平行四边形的面积公式的运用、小数除法的计算是解题的关键。
11.(1)28.8平方米
(2)160棵
【分析】(1)由题意可知,平行四边形的高就是三角形的高,根据三角形的面积公式:S=ab÷2,据此求出三角形的高,再根据平行四边形的面积公式:S=ab,据此代入数值进行计算即可求出白菜地的面积;
(2)用平行四边形的面积除以0.18即可求出共可以种多少棵。
【详解】(1)10.8×2÷(11.2-6.4)
=21.6÷4.8
=4.5(米)
6.4×4.5=28.8(平方米)
答:大白菜地一共有28.8平方米。
(2)28.8÷0.18=160(棵)
答:一共可以种160棵。
【点睛】本题考查平行四边形和三角形的面积,熟记公式是解题的关键。
12.432棵
【分析】每格占1平方米,则小方格的边长为1米,把这块菜地看作一个梯形,梯形的上底是7米,下底是11米,高是8米,利用“梯形的面积=(上底+下底)×高÷2”求出这块菜地的面积,一共种白菜的数量=这块地的面积×每平方米种白菜的数量,据此解答。
【详解】
(7+11)×8÷2×6
=18×8÷2×6
=144÷2×6
=72×6
=432(棵)
答:共约能种432棵白菜。
【点睛】掌握梯形的面积计算公式是解答题目的关键。
13.44.89元
【分析】先根据“三角形的面积=底×高÷2”求出这块三角形玻璃的面积;再根据“单价×数量=总价”求出买这块玻璃的钱数。
【详解】14.5分米=1.45米
8.6分米=0.86米
1.45×0.86÷2×72
=1.247÷2×72
=0.6235×72
=44.892(元)
≈44.89(元)
答:买这块玻璃约要44.89元。
【点睛】明确三角形的面积计算公式是解决此题的关键。
14.13.09千克
【分析】从图中可知,墙面需刷漆的面积=三角形的面积+大长方形的面积-小长方形的面积(即窗户的面积),根据三角形的面积=底×高÷2,长方形的面积=长×宽,分别代入数据计算求出墙面需刷漆的面积,再乘每平方米用油漆的质量即可;注意单位的换算:1米=10分米。
【详解】15分米=1.5米
12分米=1.2米
三角形的面积:
5×1.2÷2
=6÷2
=3(平方米)
大长方形的面积:
5×3.5=17.5(平方米)
小长方形的面积(窗户的面积):
1.5×1.2=1.8(平方米)
墙面需刷漆的面积:
3+17.5-1.8
=20.5-1.8
=18.7(平方米)
一共需要油漆:
0.7×18.7=13.09(千克)
答:刷完这面墙一共需要油漆13.09千克。
【点睛】本题考查三角形、长方形面积公式的运用,关键是弄清组合图形的面积是由哪些学过的规则图形的面积相加或相减得到,再运用相关的图形面积公式列式计算。
15.见详解;6平方厘米;见详解
【分析】根据数对表示位置的方法,数对的第一个数字表示列,第二个数字表示行;据此在图中找到A、B、C三个点的位置,再顺次连接成封闭图形,得到一个三角形;根据三角形的面积=底×高÷2,求出这个封闭图形的面积;
要画一个与封闭图形面积相等的平行四边形,根据平行四边形的面积=底×高,确定平行四边形的底和高,即可画出这个平行四边形。
【详解】封闭图形的面积:
6×4÷2
=24÷2
=12(平方厘米)
因为12=6×2,所以可以画一个底是6厘米、高是2厘米的平行四边形。
如图:
(平行四边形的画法不唯一)
【点睛】本题考查根据数对找位置以及三角形、平行四边形面积公式的运用,画平行四边形时,只需保证平行四边形的面积是12平方厘米,形状不唯一。
16.(1)形状相同;平行四边形;
(2)上底与下底的和;高;底×高;(上底+下底)×高÷2;
(3)测量数据见详解;1.125平方厘米
【分析】两个形状相同的梯形可以拼成一个平行四边形,平行四边形的面积等于梯形面积的2倍,由图可知,梯形的上底与下底的和相当于平行四边形的底,梯形的高相当于平行四边形的高,平行四边形的面积=底×高=(上底+下底)×高=梯形的面积×2,所以梯形的面积=平行四边形的面积÷2=(上底+下底)×高÷2,最后测量其中一个梯形的上底、下底、高,再把数据代入公式求出这个梯形的面积,据此解答。
【详解】(1)把两个形状相同的梯形拼成一个平行四边形。
(2)平行四边形的底相当于梯形的上底与下底的和,平行四边形的高相当于梯形的高,因为平行四边形的面积=底×高,所以梯形的面积=(上底+下底)×高÷2。
(3)
(1+2)×0.75÷2
=3×0.75÷2
=2.25÷2
=1.125(平方厘米)
答:这个梯形的面积是1.125平方厘米。
【点睛】掌握梯形面积计算公式的推导过程是解答题目的关键。
17.119000只
【分析】观察图形可知,甲鱼池由一个上底为30米、下底为80米、高为(90-40)米的直角梯形和一个长为80米、宽为40米的长方形组成,根据梯形的面积公式和长方形的面积公式求解即可得到甲鱼池的面积,已知每平方米放养甲鱼苗20只,则用甲鱼池的面积乘20即可求出放养甲鱼苗的总只数。
【详解】90-40=50(米)
(30+80)×50÷2
=110×50÷2
=5500÷2
=2750(平方米)
80×40=3200(平方米)
2750+3200=5950(平方米)
5950×20=119000(只)
答:这个甲鱼池可以放养甲鱼苗119000只。
【点睛】本题主要考查了梯形面积和长方形面积的灵活应用。
18.73125株
【分析】根据“梯形的面积=(上底+下底)×高÷2”求出这块地的面积,这块地可以种玉米的株数=这块地的面积÷每株玉米的占地面积,据此解答。
【详解】(75+120)×120÷2÷0.16
=195×120÷2÷0.16
=23400÷2÷0.16
=11700÷0.16
=73125(株)
答:这块田地可以种73125株玉米。
【点睛】本题主要考查梯形面积公式的应用,熟记公式是解答题目的关键。
19.(1)328平方米;
(2)82棵
【分析】(1)下底=上底+5米,求出下底,再根据梯形的面积=(上底+下底)×高÷2,代入数据,即可求出果园的面积。
(2)用果园的面积除以每棵梨树占地的面积,即可求出这个果园可以栽多少棵梨树。
【详解】(1)18+5=23(米)
(18+23)×16÷2
=41×16÷2
=328(平方米)
答:这个果园的面积是328平方米。
(2)328÷4=82(棵)
答:这个果园可以栽82棵梨树。
【点睛】此题的解题关键是灵活运用梯形的面积公式求解。
20.(1)32.5平方厘米
(2)32.5平方厘米;与原梯形的面积相等
(3)32.5平方厘米;与原梯形的面积相等
(4)如果把梯形的上底增加a厘米、下底减少a厘米,得到的新梯形的面积不变。因为梯形的上、下底之和不变,高不变,梯形的面积就不变
【分析】(1)梯形面积=(上底+下底)×高÷2,将数据代入公式,求出这个梯形的面积;
(2)将上底加1厘米,下底减去1厘米,求出变化后的上底和下底,再根据梯形的面积公式求出新梯形的面积,从而判断它和原来梯形的面积关系;
(3)将上底加2厘米,下底减去2厘米,求出变化后的上底和下底,再根据梯形的面积公式求出新梯形的面积,从而判断它和原来梯形的面积关系;
(4)根据(2)和(3),发现上、下底之和不变,高不变,梯形的面积就不变。
【详解】(1)(4+9)×5÷2
=13×5÷2
=65÷2
=32.5(平方厘米)
答:这个梯形的面积是32.5平方厘米。
(2)4+1=5(厘米)
9-1=8(厘米)
(5+8)×5÷2
=13×5÷2
=65÷2
=32.5(平方厘米)
答:新梯形的面积是32.5平方厘米,与原梯形的面积相等。
(3)4+2=6(厘米)
9-2=7(厘米)
(6+7)×5÷2
=13×5÷2
=65÷2
=32.5(平方厘米)
答:新梯形的面积是32.5平方厘米,与原梯形的面积相等。
(4)答:我发现如果把梯形的上底增加a厘米、下底减少a厘米,得到的新梯形的面积不变。因为梯形的上、下底之和不变,高不变,梯形的面积就不变。
【点睛】本题考查了梯形的面积,解题关键是熟记梯形的面积公式。
21.24米
【分析】观察图形可知,这条小路的长度就是三角形的高,根据三角形的面积公式:S=ab÷2,用30乘40再除以2,即可求出三角形的面积;然后用三角形的面积乘2,再除以50即可求出三角形的高,也就是小路的长度。
【详解】30×40÷2×2÷50
=1200÷2×2÷50
=600×2÷50
=1200÷50
=24(米)
答:这条小路长为24米。
【点睛】本题考查三角形的面积,灵活运用三角形的面积公式是解题的关键。
22.6.25平方分米
【分析】已知底是2.5分米,高是底的2倍,则高为(2.5×2)分米,然后根据三角形的面积公式求解即可。
【详解】2.5×2=5(分米)
2.5×5÷2
=12.5÷2
=6.25(平方分米)
答:这个三角形的面积6.25平方分米。
【点睛】本题考查了三角形面积公式的灵活应用。
23.66.6平方厘米
【分析】由题意可知,如果上底增加6.4厘米,就变成一个平行四边形,如果上底减少5.8厘米,就变成一个三角形,则梯形的下底是(6.4+5.8)厘米,上底是5.8厘米;如果上底减少5.8厘米,就变成一个三角形,此时面积就减少了21.46平方厘米,根据三角形的面积公式:S=ab÷2,据此可求出三角形的高是(21.46×2÷5.8),三角形的高也就是梯形的高,再根据梯形的面积公式:S=(a+b)h÷2,据此进行计算即可。
【详解】21.46×2÷5.8
=42.92÷5.8
=7.4(厘米)
(6.4+5.8+5.8)×7.4÷2
=18×7.4÷2
=133.2÷2
=66.6(平方厘米)
答:原来的梯形的面积是66.6平方厘米。
【点睛】本题考查三角形和梯形的面积,熟记公式是解题的关键。
24.16.2平方厘米
【分析】等边三角形的三条边都相等,用27除以3即可求三角形的一条边长,再根据三角形的面积公式:S=ab÷2,据此代入数值进行计算即可。
【详解】27÷3×3.6÷2
=9×3.6÷2
=32.4÷2
=16.2(平方厘米)
答:它的面积是16.2平方厘米。
【点睛】本题考查三角形的面积,熟记公式是解题的关键。
25.456平方米
【分析】观察图形可知,经过平移后,种植花草的部分可拼成一个长为25-1=24米,宽为20-1=19米的长方形,再根据长方形的面积公式:S=ab,据此解答即可。
【详解】(25-1)×(20-1)
=24×19
=456(平方米)
答:可种植花草部分的面积是456平方米。
【点睛】本题考查长方形的面积,结合平移的知识是解题的关键。
26.12平方米
【分析】由“有一个三角形的底是6米,如果底延长2米,面积就增加4平方米”可知,增加部分是一个底2米、高与原来三角形高相等的三角形,根据“三角形面积=底×高÷2”可知,三角形的底=面积×2÷高,求出原三角形的高,再根据三角形面积计算公式求出原来三角形的面积即可。
【详解】4×2÷2
=8÷2
=4(米)
6×4÷2
=24÷2
=12(平方米)
答:原来三角形的面积是12平方米。
【点睛】本题主要考查了三角形面积的计算,注意:增加部分是一个三角形,它的高与等于原来三角形高。
27.259.5cm2
【分析】如图所示,把正六边形分成两个完全一样的梯形,根据“梯形的面积=(上底+下底)×高÷2”求出一个梯形的面积,最后乘2求出正六边形的面积,据此解答。
【详解】
(10+20)×(17.3÷2)÷2×2
=30×8.65÷2×2
=259.5÷2×2
=129.75×2
=259.5(cm2)
答:这幅图的面积是259.5cm2。
【点睛】本题主要考查组合图形面积的计算方法,把组合图形转化为基本图形是解答题目的关键。
28.13.44平方厘米
【分析】观察图形可知,这个沙漏截面的面积=上下两个梯形的面积+中间长方形的面积,因为该沙漏的截面是一个轴对称图形,所以上下两个梯形的高相等,即(6.6-0.6)÷2=3厘米,再根据梯形的面积公式:S=(a+b)h÷2,长方形的面积公式:S=ab,据此计算即可。
【详解】(6.6-0.6)÷2
=6÷2
=3(厘米)
(4+0.4)×3÷2×2
=4.4×3÷2×2
=13.2÷2×2
=13.2(平方厘米)
0.4×0.6=0.24(平方厘米)
13.2+0.24=13.44(平方厘米)
答:这个沙漏截面的面积是13.44平方厘米。
【点睛】本题考查梯形和长方形的面积,熟记公式是解题的关键。
29.够
【分析】根据三角形的面积=底×高÷2,代入数据计算求出这块三角形空地的面积,再乘每平方米草坪的费用,即是要在这块空地上种草坪需要的钱数,最后与8万元作比较,得出结论。
【详解】8万元=80000元
40×26÷2
=1040÷2
=520(平方米)
141×520=73320(元)
73320<80000
答:8万元钱够。
【点睛】掌握三角形的面积公式,以及单价、数量、总价之间的关系是解题的关键。
30.(1)93米;(2)甲公司;(3)405平方米
【分析】(1)根据平行四边形的周长公式:C=(a+b)×2,把数据代入公式求出这个平行四边形的周长,然后减去门的宽就是需要篱笆的长度;
(2)根据单价×数量=总价,求出在甲公司购买需要多少元,然后与乙公司的报价进行比较即可;
(3)根据平行四边形的面积公式:S=ah,把数据代入公式解答。
【详解】(1)(27+20)×2-1
=47×2-1
=94-1
=93(米)
李大爷家的小花园需要93米篱笆。
(2)1.3×93=120.9(元)
120.9元<128.8元
答:选甲公司比较合算。
(3)27×15=405(平方米)
答:这个花园的面积是405平方米。
【点睛】此题主要考查平行四边形的周长公式、面积公式的灵活运用,以及单价、数量、总价三者之间的关系及应用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
