奥数拓展按比分配(含答案)数学六年级上册人教版
文档属性
| 名称 | 奥数拓展按比分配(含答案)数学六年级上册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 12:01:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
奥数拓展:按比分配-数学六年级上册人教版
1.修一条路,第一天修了总长的,第二天修24米,第三天修的与前两天修的比是3∶2,还剩没修,这条路全长是多少米?
2.小红、小英和小明三位小朋友储蓄钱数的比是,他们储蓄的平均钱数是320元。小英储蓄了多少钱?
3.学校购买篮球、足球和排球共80个,排球个数占总数的,篮球个数和足球个数的比是7∶3,学校购买的篮球比足球多多少个?
4.甲、乙两袋糖果的质量之比是3∶2,如果从甲袋糖果中拿出5千克放入乙袋,这时甲、乙两袋糖果的质量之比是1∶1。两袋糖果一共重多少千克?
5.小红读一本故事书,第一天读了全书的,第二天读了36页。这时已读页数与剩下页数的比是5∶7,小红再读多少页就能读完这本书?
6.学校买来一批书,分给高年级后,剩下的按4∶3的比分给中年级和低年级。已知中年级分得240本,这批书一共有多少本?
7.在直角三角形ABC中,这个三角形的面积是90平方厘米,D是BC的中点,E是AD中一点,AE与ED的比是2∶1,求阴影部分的面积?
8.甲、乙两小学原有图书本数之比是7:5,如果甲校赠给乙校750本,乙校又回赠给甲校100本,那么,甲、乙两校的图书本数之比变为3:4.问甲、乙两校原有图书各多少本?
9.某工会男女会员的人数之比是3∶2,分为甲、乙、丙三组,已知甲、乙、丙三组的人数比是10∶8∶7,甲组中男女会员的人数之比是3∶1,乙组中男女会员的人数之比是5∶3,求丙组中男女会员的人数之比。
10.王叔叔12月份接到加工一批零件的任务,他第一周加工后,已加工零件个数和剩下零件个数的比是1∶3,第二周加工了总任务的,已知两周一共加工了140个零件。王叔叔接到的任务是一共要加工多少个零件?
11.一个长方体的长、宽、高的比是5∶2∶3,这个长方形的棱长之和是80厘米。这个长方体的体积是多少立方厘米?
12.两个水池内有金鱼若干条,数目相同。亮亮和红红进行捞鱼比赛,第一个水池内的金鱼被捞完时,亮亮和红红所捞到的金鱼数目比是3∶4;捞完第二个水池内的金鱼时,亮亮比第一次多捞33条,与红红捞到的金鱼数目比是5∶3。那么每个水池内有金鱼多少条?
13.小明看一本故事书,第一天看的页数与这本书总页数的比是3∶10,如果再看30页,正好看完这本书的一半,这本书共有多少页?
14.甲、乙两人从山脚下同一点沿一条道路同时出发,进行爬山比赛,他们下山速度都是各自上山速度的2倍,当甲爬到山顶时,乙离山顶还有72米。当甲回到山脚下,乙已返回到半山腰,山下到山顶的路程是多少米?
15.甲、乙、丙三个班共植树85棵,甲班比乙班多植1棵,丙班与乙班植树棵数的比是,甲班植树多少棵?
16.某高速公路收费站对过往车辆的收费标准:大型车30元/辆,中型车15元/辆,小型车10元/辆。一天,通过该收费站的大型车和中型车的辆数之比是5∶6,中型车与小型车的辆数之比是4∶11,小型车的通行费总数比大型车多270元,求这天通过收费站的大型车、中型车及小型车各有多少辆和收费总数是多少元?
17.甲、乙、丙三村合修一条公路,修完后甲村受益是丙村的3倍,乙村受益的等于甲村受益的。三个村原来协商按各个村受益的多少来派出劳力修公路,后来因丙村抽不出劳力,经再次协商,丙村抽不出的劳力由甲、乙两村分担,丙村共付给甲、乙两村工钱1200元,结果甲村共派45人,乙村共派35人完成修路任务。问:甲、乙两村各应分得工钱多少元?
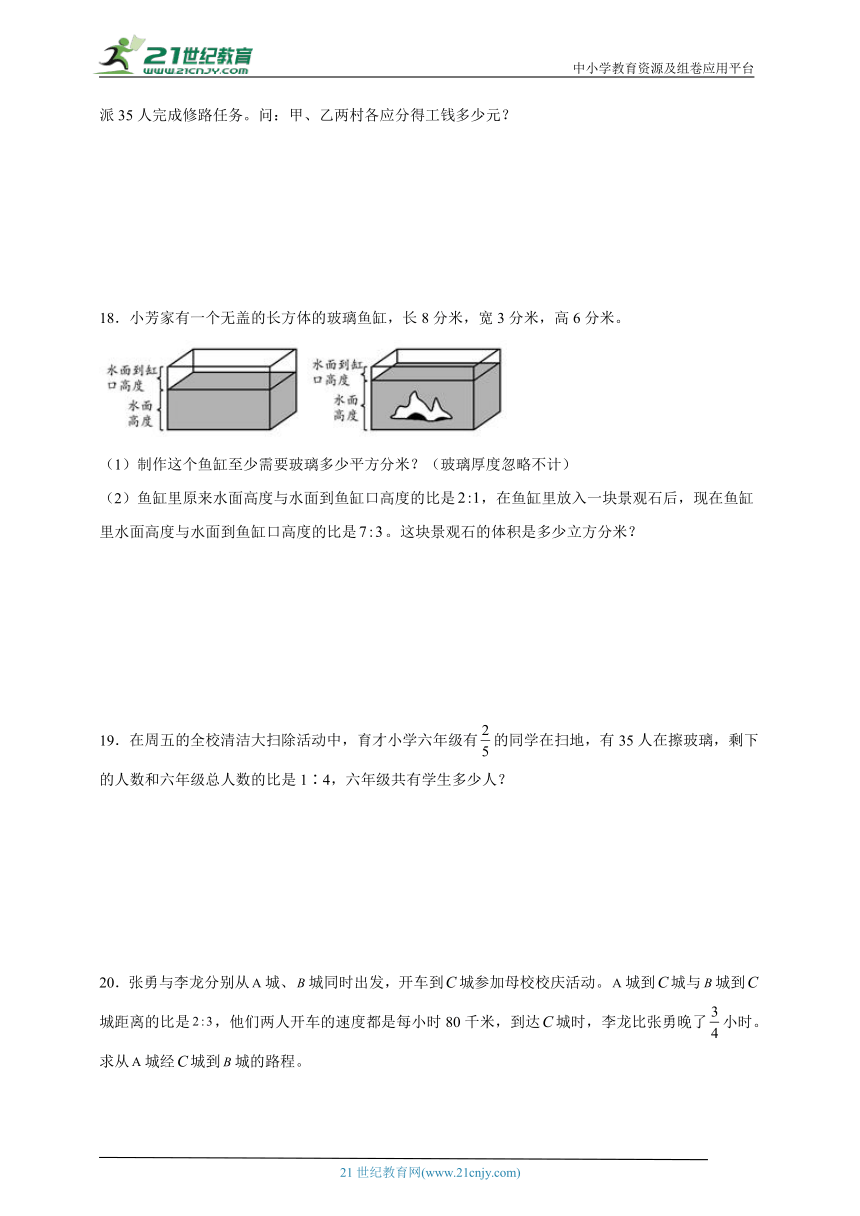
18.小芳家有一个无盖的长方体的玻璃鱼缸,长8分米,宽3分米,高6分米。
(1)制作这个鱼缸至少需要玻璃多少平方分米?(玻璃厚度忽略不计)
(2)鱼缸里原来水面高度与水面到鱼缸口高度的比是,在鱼缸里放入一块景观石后,现在鱼缸里水面高度与水面到鱼缸口高度的比是。这块景观石的体积是多少立方分米?
19.在周五的全校清洁大扫除活动中,育才小学六年级有的同学在扫地,有35人在擦玻璃,剩下的人数和六年级总人数的比是1∶4,六年级共有学生多少人?
20.张勇与李龙分别从城、城同时出发,开车到城参加母校校庆活动。城到城与城到城距离的比是,他们两人开车的速度都是每小时80千米,到达城时,李龙比张勇晚了小时。求从城经城到城的路程。
21.猴王召集猴子们开会,点名时发现缺席只数是出席只数的,他很生气,刚要发火,又跑来了2只猴子,这时缺席只数是出席只数的,这群猴子共有多少只?
参考答案:
1.180米
【分析】根据题意先将第三天修的占全长的几分之几求出来,再利用减法求出第二天修的占全长的几分之几,最后利用除法求出这条路全长是多少米。
【详解】24÷[1---(1-)×]
=24÷[1---×]
=24÷[1---]
=24÷
=180(米)
答:这条路全长是180米。
【点睛】本题考查了分数除法的应用,能够依据题意求出第二天修的占全长的几分之几是解题的关键。
2.360元
【分析】他们储蓄的平均钱数是320元,那么总共是960元,小红、小英和小明的钱数分别是1份、3份和4份,8份是960元,1份是120元。
【详解】
(元)
(元)
答:小英储蓄了360元钱。
【点睛】本题考查的是按比分配问题,按比分配问题与和倍问题类似,先求出一份量,再计算多份量。
3.20个
【分析】先求出篮球和足球总共多少个,再按照篮球和足球占它们总数的分率进行求解。
【详解】
答:篮球比足球多20个。
【点睛】本题也可以分别求出篮球和足球的数量,再计算二者的差。
4.50千克
【分析】甲、乙两袋糖果的质量之比是3∶2,甲袋比乙袋多3-2份,甲袋拿出多出份数的一半放入乙袋,两袋质量相等,据此求出一份数,用一份数×总份数即可。
【详解】5÷[(3-2)÷2]
=5÷(1÷2)
=5÷0.5
=10(千克)
10×(3+2)
=10×5
=50(千克)
答:两袋糖果一共重50千克。
【点睛】关键是确定甲袋放入乙袋的质量的对应的份数,求出一份数。
5.84页
【分析】设这本书有x页,通过已读页数与剩下页数的比可知,已读页数占总页数的,未读页数占总页数的,根据总页数×第一天读的对应分率+第二天读的页数=总页数×已读页数的对应分率,列出方程求出全书总页数,用全书总页数×未读页数的对应分率即可。
【详解】解:设这本书有x页。
(页)
答:小红再读84页就能读完这本书。
【点睛】关键是找到等量关系,理解分数乘法和比的意义。
6.700本
【分析】用 算出的是分给高年级后剩下的书的本数,420本对应的分率是 ,所以用可求出这批书一共有多少本。
【详解】240÷=420(本)
420÷
=420÷
=700(本)
答:这批书一共有700本。
【点睛】本题考查按比例分配、分数除法,解答本题的关键是掌握按比例分配解题的方法。
7.15平方厘米
【分析】因为D是BC的中点,所以S△ACD=S△ABC;
因为AE与ED的比是2∶1,所以AD∶ED=3∶1,即S△CED=S△ACD;
因此S△CED=S△ABC××=90××=15(平方厘米)
【详解】90××=15(平方厘米)
【点睛】由题目里的中点及线段的比,再结合三角形的面积的特点,能够确定所求三角形面积与已知三角形面积的倍分关系,再依据倍分关系可计算求得阴影部分面积。
8.甲校原有图书2450本,乙校原有图书1750本。
【分析】根据题意可知:甲校原有的图书本数占总数的,现有的图书本数占总数的,由于是在两个学校之间的赠与,所以两校的图书总本数不变,可以把总本数看作“1”;由甲赠给乙750本,乙又回赠甲100本,相当于甲赠给了乙650本;那么650本就占总数的(),用除法计算求得单位“1”的量;再用按比例分配的方法分别求出甲、乙两校原有图书的本数;列式计算即可解决。
【详解】甲校原有图书本数占总数的:7÷(7+5)=,
甲校现有图书本数占总数的:3÷(3+4)=,
图书总本数:(750﹣100)÷(),
=650÷,
=4200(本);
甲原有:4200×=2450(本),
乙原有:4200×=1750(本);
答:甲校原有图书2450本,乙校原有图书1750本。
【点睛】解决此题关键是理解甲赠给乙750本,乙又回赠甲100本,相当于甲赠给了乙650本,进而求出650本对应的分率,求得图书总本数,再用按比例分配的方法分别求出甲、乙两校原有图书的本数。
9.5∶9
【分析】根据甲、乙、丙三组人数的比为10∶8∶7,可设甲组人数为10x,乙组人数为8x,丙组人数为7x,那么三组共有人数为25x;再根据男女会员的人数之比是3:2,可求得男会员是15x人,女会员是10x人;由甲组中男女会员的人数之比是3∶1,求得甲组男会员是7.5x人,女会员是2.5x人;乙组中男女会员的人数比是5∶3,求得乙组男会员是5x人,女会员是3x人,那么丙组的男会员就是15x-7.5x-5x=2.5x人,丙组的女会员就是10x-2.5x-3x=4.5x人,那么丙组男女会员人数之比是2.5x∶4.5x=5∶9。
【详解】解:设甲组为10x人,乙组为8x人,丙组为7x人,
则三组共有会员:10x+8x+7x=25x(人),
俱乐部有男会员:25x×=15x(人),俱乐部有女会员:25x×=10x(人),
甲组有男会员:10x×=7.5x(人),甲组有女会员:10x-7.5x=2.5x(人),
乙组有男会员:8x×=5x(人),乙组有女会员:8x-5x=3x(人),
丙组有男会员:15x-7.5x-5x=2.5x(人),丙组有女会员:10x-2.5x-3x=4.5x(人),
则丙组中男女会员人数之比:2.5x∶4.5x=5∶9。
答:丙组中男女会员人数之比是5∶9。
【点睛】此题考查比的应用,解决此题关键是根据题意先求得总人数和俱乐部有男女会员的人数,然后分别求得甲乙两组中男女会员的人数,进而分别求得丙组中男女会员人数,再写出比并化简比即可。
10.240个
【分析】根据条件“他第一周加工后,已加工零件个数和剩下零件个数的比是1∶3”可知,第一周完成的占全部任务的=,然后用两周一共加工的零件总个数÷两周一共加工的占总个数的分率=要加工的零件总个数,据此列式解答。
【详解】第一周完成了=
140÷(+)
=140÷
=140×
=240(个)
答:王叔叔接到的任务是一共要加工240个零件。
【点睛】题目中不易理解的一句话是“他第一周加工后,已加工零件个数和剩下零件个数的比是1∶3”,我们需要依据比与分数的关系,把它转化成一个表示第一周完成的零件个数占零件总数的分率。
11.240立方厘米
【分析】长方体的的12条棱长由4条长、4条宽、4条高组成,那么长、宽、高的长度之和为80÷4=20厘米;根据长方体长、宽、高的比是5∶2∶3,把长看作5份,宽看作2份,高看作3份,长、宽、高的长度之和为10份,据此解答即可。
【详解】80÷4÷(5+2+3)
=20÷10
=2(厘米)
(2×5)×(2×2)×(2×3)
=10×4×6
=240(立方厘米)
答:这个长方体的体积是240立方厘米。
【点睛】本题考查长方体的体积、按比例分配,解答本题的关键是掌握按比例分配的方法。
12.168条
【分析】捞完第二个水池内的金鱼时,亮亮与红红捞到的金鱼数目比是5∶3,亮亮捞到的金鱼数目占两人的,第一个水池内的金鱼被捞完时,亮亮和红红所捞到的金鱼数目比是3∶4,亮亮捞到的金鱼数目占两人的,多了-,多了33条,用多出来的条数÷对应分率即可。
【详解】33÷(-)
=33÷
=168(条)
答:每个水池内有金鱼168条。
【点睛】将每个水池内的金鱼条数看作单位“1”,关键是找到33条金鱼的对应分率。
13.150页
【分析】第一天看的页数与这本书总页数的比是3∶10,则第一天看的页数是这本书总页数的,如果再看30页,正好看完这本书的一半,则30页占这本书总页数的-,最后求出这本书的总页数即可。
【详解】30÷(-)
=30÷
=150(页)
答:这本书共有150页。
【点睛】本题考查比与分数的关系、分数除法,解答本题的关键是掌握比与分数之间的关系。
14.432米
【分析】根据题意,我们可以先把山顶到山下的距离看作是单位“1”,同时假设甲乙两人到达山顶后继续上行;由题意可知,他们下山速度都是各自上山的2倍,所以甲下山的路程相当于上山路程的,同理可知,乙下山至半山腰相当于上山路程的;由甲乙两人行走的时间相同,我们可以得出甲乙两人的路程比,继而得到乙行的路程是甲的,结合“甲爬到山顶沿原路返回与乙相遇时,乙离山顶还有72米”可得算式72÷(1-),计算可得到答案。
【详解】1÷2=
÷2=
甲乙的路程比为(1+)∶(1+)=6∶5
即乙行的路程是甲的
72÷(1-)
=72÷
=432(米)
答:山下到山顶的路程是432米。
【点睛】关键点:①利用甲乙二人下山的速度都是各自上山的2倍,求出甲乙二人的路程比;②把山顶到山下的距离看作是单位“1”,用分数除法计算求得答案。
15.25棵
【分析】①如果用85-1,把甲班多于乙班的1棵减掉,则同时丙班与乙班植树棵数的比就不是3∶2了;②因为丙班与乙班植树棵数的比是3∶2,若想凭已知条件求出甲、乙、丙3个班级植树的比,又求不出来;③我们可以顺向思维,列方程解答。设乙班植树x棵,则甲班植树(x+1)棵,再根据丙班与乙班植树棵数的比,用含有x的式子来表示丙班植树棵数,最后将三者相加等于85棵,解这个方程即可。
【详解】解:设乙班植树x棵,则甲班植树(x+1)棵,丙班植树x棵,由题意得,
(x+1)+x+x=85
3.5x+1=85
3.5x=84
x=24
24+1=25(棵)
答:甲班植树25棵。
【点睛】题意有些复杂,用方程解答比较顺利,这也体现了方程顺向思维的优势。
16.90辆、108辆、297辆;7290元
【分析】首先将大型车、中型车、小型车通过的辆数写成连比形式,即得出三种车的份数比,设出未知数,再根据“小型车的通行费总数比大型车多270元”,求解即可。
【详解】解:大型车和中型车的辆数之比是5∶6,中型车与小型车的辆数之比是4∶11,
所以大型车、中型车、小型车通过的辆数之比为:10∶12∶33;
假设大型车有10x辆,则中型车有12x辆,小型车有33x辆
33x×10-10x×30=270
330x-300x=270
30x=270
x=9
大型车:10×9=90(辆)
中型车:12×9=108(辆)
小型车:33×9=297(辆)
总钱数是:10×9×30+12×9×15+33×9×10
=2700+1620+2970
=7290(元)
答:这天通过收费站的大型车、中型车及小型车分别有90辆、108辆、297辆;收费总数是7290元。
【点睛】把通过的三种车辆数写成连比形式并转化为份数比是解题关键。
17.甲村得工钱:900元
乙村得工钱:300元
【分析】把丙村收益看作单位“1”,则甲村收益是“3”,由题意可得:乙村受益×=甲村受益×,则乙村受益为:3×÷=,则甲、乙、丙三村受益比为:3∶∶1=9∶8∶3,由题意可得:三村所派人数的比即为9∶8∶3,总人数是:45+35=80(人);80人按9∶8∶3比例分配为:36人、32人、12人;即甲村需36人,乙村需32人,丙村需12人;所以甲村有45-36=9(人)在为丙村修路;而乙村有35-32=3(人)在为丙村修路;然后根据人数的比进行解答即可。
【详解】把丙村收益看作单位“1”,则甲村收益是“3”,由题意可得:乙村受益×=甲村受益×,则乙村受益为:3×÷=,则甲、乙、丙三村受益比为:3∶∶1=9∶8∶3
9+8+3=20(份)
甲分配人数:
(45+35)÷20×9
=80×20×9
=36(人)
乙分配人数:
(45+35)÷20×8
=80×20×8
=32(人)
丙分配人数:
(45+35)÷20×3
=80×20×3
=12(人)
45-36=9(人),35-32=3(人)
甲村应得工钱:1200×=1200×=900(元)
乙村应得工钱:1200×=1200×=300(元)
答:甲村应该分得900元,乙村应分得300元。
【点睛】解答此题应结合题意,明确先要求出三个村的分配人数,然后根据按比例分配知识进行解答即可。
18.(1)156平方分米
(2)4.8立方分米
【分析】(1)由题意可知,长方体的玻璃鱼缸是无盖的,所以只要计算5个面的面积即可。
(2)长方体的体积=长×宽×高,没放景观石前水面高度:=4 (分米),放景观石后水面高度:=4.2 (分米),景观石体积:(4.2- 4) ×8×3= 4.8 (立方分米)。
【详解】(1)8×3+8×6×2+6×3×2
=24+96+36
=156 (平方分米)
答:制作这个鱼缸至少需要玻璃156平方分米。
(2)没放景观石前水面高度:=4 (分米)
放景观石后水面高度:=4.2 (分米)
景观石体积:(4.2- 4) ×8×3
=0.2×8×3
= 4.8 (立方分米)
答:这块景观石的体积是4.8立方分米。
【点睛】本题考查长方体的表面积和体积公式的实际应用、按比例分配,解答本题的关键是理解没放景观石前水面高度:=4 (分米),放景观石后水面高度:=4.2 (分米)。
19.100人
【分析】把六年级总人数看作单位“1”,育才小学六年级有的同学在扫地,有35人在擦玻璃,剩下的人数和六年级总人数的比是1∶4,则剩下的人数的分率为,则35人对应的分率为1--,运用除法即可求出六年级总人数。
【详解】35÷(1--)
=35÷
=100(人)
答:六年级共有学生100人。
【点睛】本题考查分数除法、比、分数减法,解答本题的关键是找准单位“1”,根据已知一个数的几分之几是多少,求这个数用除法计算即可。
20.300千米
【分析】根据题意得出:李龙比张勇晚了小时,则李龙比张勇多走了80×=60千米,又因为A城到C城与B城到C城的距离比是2∶3,则李龙比张勇多走的路程60千米占AB全程的,用除法解答即可。
【详解】80×÷
=60÷
=300(千米)
答:从城经城到城的路程是300千米。
【点睛】本题考查比的应用,解决本题关键是根据题意找出李龙多走的路程是全程的几分之几,用除法解答即可。
21.144只
【分析】开始缺席只数是出席只数的,缺席数量∶出席的数量,那么缺席的猴子数就是猴子总数的;同理后来缺席只数是出席只数的,缺席的猴子是猴子总数的,那么减少的分数对应的数量就2只,求总数用除法。
【详解】当缺席只数是出席只数的,缺席的猴子数就是猴子总数的;当缺席只数是出席只数的,缺席的猴子是猴子总数的;
,
(只)
答:这群猴子有144只。
【点评】本题考查分数除法的实际应用,解答本题的关键是理解不变的数量是猴子的总数,所以把猴子的总数看成单位“1”,分别找出两次缺席猴子数占总数的几分之几,再根据它们的差对应的数量是2,来求猴子总数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
奥数拓展:按比分配-数学六年级上册人教版
1.修一条路,第一天修了总长的,第二天修24米,第三天修的与前两天修的比是3∶2,还剩没修,这条路全长是多少米?
2.小红、小英和小明三位小朋友储蓄钱数的比是,他们储蓄的平均钱数是320元。小英储蓄了多少钱?
3.学校购买篮球、足球和排球共80个,排球个数占总数的,篮球个数和足球个数的比是7∶3,学校购买的篮球比足球多多少个?
4.甲、乙两袋糖果的质量之比是3∶2,如果从甲袋糖果中拿出5千克放入乙袋,这时甲、乙两袋糖果的质量之比是1∶1。两袋糖果一共重多少千克?
5.小红读一本故事书,第一天读了全书的,第二天读了36页。这时已读页数与剩下页数的比是5∶7,小红再读多少页就能读完这本书?
6.学校买来一批书,分给高年级后,剩下的按4∶3的比分给中年级和低年级。已知中年级分得240本,这批书一共有多少本?
7.在直角三角形ABC中,这个三角形的面积是90平方厘米,D是BC的中点,E是AD中一点,AE与ED的比是2∶1,求阴影部分的面积?
8.甲、乙两小学原有图书本数之比是7:5,如果甲校赠给乙校750本,乙校又回赠给甲校100本,那么,甲、乙两校的图书本数之比变为3:4.问甲、乙两校原有图书各多少本?
9.某工会男女会员的人数之比是3∶2,分为甲、乙、丙三组,已知甲、乙、丙三组的人数比是10∶8∶7,甲组中男女会员的人数之比是3∶1,乙组中男女会员的人数之比是5∶3,求丙组中男女会员的人数之比。
10.王叔叔12月份接到加工一批零件的任务,他第一周加工后,已加工零件个数和剩下零件个数的比是1∶3,第二周加工了总任务的,已知两周一共加工了140个零件。王叔叔接到的任务是一共要加工多少个零件?
11.一个长方体的长、宽、高的比是5∶2∶3,这个长方形的棱长之和是80厘米。这个长方体的体积是多少立方厘米?
12.两个水池内有金鱼若干条,数目相同。亮亮和红红进行捞鱼比赛,第一个水池内的金鱼被捞完时,亮亮和红红所捞到的金鱼数目比是3∶4;捞完第二个水池内的金鱼时,亮亮比第一次多捞33条,与红红捞到的金鱼数目比是5∶3。那么每个水池内有金鱼多少条?
13.小明看一本故事书,第一天看的页数与这本书总页数的比是3∶10,如果再看30页,正好看完这本书的一半,这本书共有多少页?
14.甲、乙两人从山脚下同一点沿一条道路同时出发,进行爬山比赛,他们下山速度都是各自上山速度的2倍,当甲爬到山顶时,乙离山顶还有72米。当甲回到山脚下,乙已返回到半山腰,山下到山顶的路程是多少米?
15.甲、乙、丙三个班共植树85棵,甲班比乙班多植1棵,丙班与乙班植树棵数的比是,甲班植树多少棵?
16.某高速公路收费站对过往车辆的收费标准:大型车30元/辆,中型车15元/辆,小型车10元/辆。一天,通过该收费站的大型车和中型车的辆数之比是5∶6,中型车与小型车的辆数之比是4∶11,小型车的通行费总数比大型车多270元,求这天通过收费站的大型车、中型车及小型车各有多少辆和收费总数是多少元?
17.甲、乙、丙三村合修一条公路,修完后甲村受益是丙村的3倍,乙村受益的等于甲村受益的。三个村原来协商按各个村受益的多少来派出劳力修公路,后来因丙村抽不出劳力,经再次协商,丙村抽不出的劳力由甲、乙两村分担,丙村共付给甲、乙两村工钱1200元,结果甲村共派45人,乙村共派35人完成修路任务。问:甲、乙两村各应分得工钱多少元?
18.小芳家有一个无盖的长方体的玻璃鱼缸,长8分米,宽3分米,高6分米。
(1)制作这个鱼缸至少需要玻璃多少平方分米?(玻璃厚度忽略不计)
(2)鱼缸里原来水面高度与水面到鱼缸口高度的比是,在鱼缸里放入一块景观石后,现在鱼缸里水面高度与水面到鱼缸口高度的比是。这块景观石的体积是多少立方分米?
19.在周五的全校清洁大扫除活动中,育才小学六年级有的同学在扫地,有35人在擦玻璃,剩下的人数和六年级总人数的比是1∶4,六年级共有学生多少人?
20.张勇与李龙分别从城、城同时出发,开车到城参加母校校庆活动。城到城与城到城距离的比是,他们两人开车的速度都是每小时80千米,到达城时,李龙比张勇晚了小时。求从城经城到城的路程。
21.猴王召集猴子们开会,点名时发现缺席只数是出席只数的,他很生气,刚要发火,又跑来了2只猴子,这时缺席只数是出席只数的,这群猴子共有多少只?
参考答案:
1.180米
【分析】根据题意先将第三天修的占全长的几分之几求出来,再利用减法求出第二天修的占全长的几分之几,最后利用除法求出这条路全长是多少米。
【详解】24÷[1---(1-)×]
=24÷[1---×]
=24÷[1---]
=24÷
=180(米)
答:这条路全长是180米。
【点睛】本题考查了分数除法的应用,能够依据题意求出第二天修的占全长的几分之几是解题的关键。
2.360元
【分析】他们储蓄的平均钱数是320元,那么总共是960元,小红、小英和小明的钱数分别是1份、3份和4份,8份是960元,1份是120元。
【详解】
(元)
(元)
答:小英储蓄了360元钱。
【点睛】本题考查的是按比分配问题,按比分配问题与和倍问题类似,先求出一份量,再计算多份量。
3.20个
【分析】先求出篮球和足球总共多少个,再按照篮球和足球占它们总数的分率进行求解。
【详解】
答:篮球比足球多20个。
【点睛】本题也可以分别求出篮球和足球的数量,再计算二者的差。
4.50千克
【分析】甲、乙两袋糖果的质量之比是3∶2,甲袋比乙袋多3-2份,甲袋拿出多出份数的一半放入乙袋,两袋质量相等,据此求出一份数,用一份数×总份数即可。
【详解】5÷[(3-2)÷2]
=5÷(1÷2)
=5÷0.5
=10(千克)
10×(3+2)
=10×5
=50(千克)
答:两袋糖果一共重50千克。
【点睛】关键是确定甲袋放入乙袋的质量的对应的份数,求出一份数。
5.84页
【分析】设这本书有x页,通过已读页数与剩下页数的比可知,已读页数占总页数的,未读页数占总页数的,根据总页数×第一天读的对应分率+第二天读的页数=总页数×已读页数的对应分率,列出方程求出全书总页数,用全书总页数×未读页数的对应分率即可。
【详解】解:设这本书有x页。
(页)
答:小红再读84页就能读完这本书。
【点睛】关键是找到等量关系,理解分数乘法和比的意义。
6.700本
【分析】用 算出的是分给高年级后剩下的书的本数,420本对应的分率是 ,所以用可求出这批书一共有多少本。
【详解】240÷=420(本)
420÷
=420÷
=700(本)
答:这批书一共有700本。
【点睛】本题考查按比例分配、分数除法,解答本题的关键是掌握按比例分配解题的方法。
7.15平方厘米
【分析】因为D是BC的中点,所以S△ACD=S△ABC;
因为AE与ED的比是2∶1,所以AD∶ED=3∶1,即S△CED=S△ACD;
因此S△CED=S△ABC××=90××=15(平方厘米)
【详解】90××=15(平方厘米)
【点睛】由题目里的中点及线段的比,再结合三角形的面积的特点,能够确定所求三角形面积与已知三角形面积的倍分关系,再依据倍分关系可计算求得阴影部分面积。
8.甲校原有图书2450本,乙校原有图书1750本。
【分析】根据题意可知:甲校原有的图书本数占总数的,现有的图书本数占总数的,由于是在两个学校之间的赠与,所以两校的图书总本数不变,可以把总本数看作“1”;由甲赠给乙750本,乙又回赠甲100本,相当于甲赠给了乙650本;那么650本就占总数的(),用除法计算求得单位“1”的量;再用按比例分配的方法分别求出甲、乙两校原有图书的本数;列式计算即可解决。
【详解】甲校原有图书本数占总数的:7÷(7+5)=,
甲校现有图书本数占总数的:3÷(3+4)=,
图书总本数:(750﹣100)÷(),
=650÷,
=4200(本);
甲原有:4200×=2450(本),
乙原有:4200×=1750(本);
答:甲校原有图书2450本,乙校原有图书1750本。
【点睛】解决此题关键是理解甲赠给乙750本,乙又回赠甲100本,相当于甲赠给了乙650本,进而求出650本对应的分率,求得图书总本数,再用按比例分配的方法分别求出甲、乙两校原有图书的本数。
9.5∶9
【分析】根据甲、乙、丙三组人数的比为10∶8∶7,可设甲组人数为10x,乙组人数为8x,丙组人数为7x,那么三组共有人数为25x;再根据男女会员的人数之比是3:2,可求得男会员是15x人,女会员是10x人;由甲组中男女会员的人数之比是3∶1,求得甲组男会员是7.5x人,女会员是2.5x人;乙组中男女会员的人数比是5∶3,求得乙组男会员是5x人,女会员是3x人,那么丙组的男会员就是15x-7.5x-5x=2.5x人,丙组的女会员就是10x-2.5x-3x=4.5x人,那么丙组男女会员人数之比是2.5x∶4.5x=5∶9。
【详解】解:设甲组为10x人,乙组为8x人,丙组为7x人,
则三组共有会员:10x+8x+7x=25x(人),
俱乐部有男会员:25x×=15x(人),俱乐部有女会员:25x×=10x(人),
甲组有男会员:10x×=7.5x(人),甲组有女会员:10x-7.5x=2.5x(人),
乙组有男会员:8x×=5x(人),乙组有女会员:8x-5x=3x(人),
丙组有男会员:15x-7.5x-5x=2.5x(人),丙组有女会员:10x-2.5x-3x=4.5x(人),
则丙组中男女会员人数之比:2.5x∶4.5x=5∶9。
答:丙组中男女会员人数之比是5∶9。
【点睛】此题考查比的应用,解决此题关键是根据题意先求得总人数和俱乐部有男女会员的人数,然后分别求得甲乙两组中男女会员的人数,进而分别求得丙组中男女会员人数,再写出比并化简比即可。
10.240个
【分析】根据条件“他第一周加工后,已加工零件个数和剩下零件个数的比是1∶3”可知,第一周完成的占全部任务的=,然后用两周一共加工的零件总个数÷两周一共加工的占总个数的分率=要加工的零件总个数,据此列式解答。
【详解】第一周完成了=
140÷(+)
=140÷
=140×
=240(个)
答:王叔叔接到的任务是一共要加工240个零件。
【点睛】题目中不易理解的一句话是“他第一周加工后,已加工零件个数和剩下零件个数的比是1∶3”,我们需要依据比与分数的关系,把它转化成一个表示第一周完成的零件个数占零件总数的分率。
11.240立方厘米
【分析】长方体的的12条棱长由4条长、4条宽、4条高组成,那么长、宽、高的长度之和为80÷4=20厘米;根据长方体长、宽、高的比是5∶2∶3,把长看作5份,宽看作2份,高看作3份,长、宽、高的长度之和为10份,据此解答即可。
【详解】80÷4÷(5+2+3)
=20÷10
=2(厘米)
(2×5)×(2×2)×(2×3)
=10×4×6
=240(立方厘米)
答:这个长方体的体积是240立方厘米。
【点睛】本题考查长方体的体积、按比例分配,解答本题的关键是掌握按比例分配的方法。
12.168条
【分析】捞完第二个水池内的金鱼时,亮亮与红红捞到的金鱼数目比是5∶3,亮亮捞到的金鱼数目占两人的,第一个水池内的金鱼被捞完时,亮亮和红红所捞到的金鱼数目比是3∶4,亮亮捞到的金鱼数目占两人的,多了-,多了33条,用多出来的条数÷对应分率即可。
【详解】33÷(-)
=33÷
=168(条)
答:每个水池内有金鱼168条。
【点睛】将每个水池内的金鱼条数看作单位“1”,关键是找到33条金鱼的对应分率。
13.150页
【分析】第一天看的页数与这本书总页数的比是3∶10,则第一天看的页数是这本书总页数的,如果再看30页,正好看完这本书的一半,则30页占这本书总页数的-,最后求出这本书的总页数即可。
【详解】30÷(-)
=30÷
=150(页)
答:这本书共有150页。
【点睛】本题考查比与分数的关系、分数除法,解答本题的关键是掌握比与分数之间的关系。
14.432米
【分析】根据题意,我们可以先把山顶到山下的距离看作是单位“1”,同时假设甲乙两人到达山顶后继续上行;由题意可知,他们下山速度都是各自上山的2倍,所以甲下山的路程相当于上山路程的,同理可知,乙下山至半山腰相当于上山路程的;由甲乙两人行走的时间相同,我们可以得出甲乙两人的路程比,继而得到乙行的路程是甲的,结合“甲爬到山顶沿原路返回与乙相遇时,乙离山顶还有72米”可得算式72÷(1-),计算可得到答案。
【详解】1÷2=
÷2=
甲乙的路程比为(1+)∶(1+)=6∶5
即乙行的路程是甲的
72÷(1-)
=72÷
=432(米)
答:山下到山顶的路程是432米。
【点睛】关键点:①利用甲乙二人下山的速度都是各自上山的2倍,求出甲乙二人的路程比;②把山顶到山下的距离看作是单位“1”,用分数除法计算求得答案。
15.25棵
【分析】①如果用85-1,把甲班多于乙班的1棵减掉,则同时丙班与乙班植树棵数的比就不是3∶2了;②因为丙班与乙班植树棵数的比是3∶2,若想凭已知条件求出甲、乙、丙3个班级植树的比,又求不出来;③我们可以顺向思维,列方程解答。设乙班植树x棵,则甲班植树(x+1)棵,再根据丙班与乙班植树棵数的比,用含有x的式子来表示丙班植树棵数,最后将三者相加等于85棵,解这个方程即可。
【详解】解:设乙班植树x棵,则甲班植树(x+1)棵,丙班植树x棵,由题意得,
(x+1)+x+x=85
3.5x+1=85
3.5x=84
x=24
24+1=25(棵)
答:甲班植树25棵。
【点睛】题意有些复杂,用方程解答比较顺利,这也体现了方程顺向思维的优势。
16.90辆、108辆、297辆;7290元
【分析】首先将大型车、中型车、小型车通过的辆数写成连比形式,即得出三种车的份数比,设出未知数,再根据“小型车的通行费总数比大型车多270元”,求解即可。
【详解】解:大型车和中型车的辆数之比是5∶6,中型车与小型车的辆数之比是4∶11,
所以大型车、中型车、小型车通过的辆数之比为:10∶12∶33;
假设大型车有10x辆,则中型车有12x辆,小型车有33x辆
33x×10-10x×30=270
330x-300x=270
30x=270
x=9
大型车:10×9=90(辆)
中型车:12×9=108(辆)
小型车:33×9=297(辆)
总钱数是:10×9×30+12×9×15+33×9×10
=2700+1620+2970
=7290(元)
答:这天通过收费站的大型车、中型车及小型车分别有90辆、108辆、297辆;收费总数是7290元。
【点睛】把通过的三种车辆数写成连比形式并转化为份数比是解题关键。
17.甲村得工钱:900元
乙村得工钱:300元
【分析】把丙村收益看作单位“1”,则甲村收益是“3”,由题意可得:乙村受益×=甲村受益×,则乙村受益为:3×÷=,则甲、乙、丙三村受益比为:3∶∶1=9∶8∶3,由题意可得:三村所派人数的比即为9∶8∶3,总人数是:45+35=80(人);80人按9∶8∶3比例分配为:36人、32人、12人;即甲村需36人,乙村需32人,丙村需12人;所以甲村有45-36=9(人)在为丙村修路;而乙村有35-32=3(人)在为丙村修路;然后根据人数的比进行解答即可。
【详解】把丙村收益看作单位“1”,则甲村收益是“3”,由题意可得:乙村受益×=甲村受益×,则乙村受益为:3×÷=,则甲、乙、丙三村受益比为:3∶∶1=9∶8∶3
9+8+3=20(份)
甲分配人数:
(45+35)÷20×9
=80×20×9
=36(人)
乙分配人数:
(45+35)÷20×8
=80×20×8
=32(人)
丙分配人数:
(45+35)÷20×3
=80×20×3
=12(人)
45-36=9(人),35-32=3(人)
甲村应得工钱:1200×=1200×=900(元)
乙村应得工钱:1200×=1200×=300(元)
答:甲村应该分得900元,乙村应分得300元。
【点睛】解答此题应结合题意,明确先要求出三个村的分配人数,然后根据按比例分配知识进行解答即可。
18.(1)156平方分米
(2)4.8立方分米
【分析】(1)由题意可知,长方体的玻璃鱼缸是无盖的,所以只要计算5个面的面积即可。
(2)长方体的体积=长×宽×高,没放景观石前水面高度:=4 (分米),放景观石后水面高度:=4.2 (分米),景观石体积:(4.2- 4) ×8×3= 4.8 (立方分米)。
【详解】(1)8×3+8×6×2+6×3×2
=24+96+36
=156 (平方分米)
答:制作这个鱼缸至少需要玻璃156平方分米。
(2)没放景观石前水面高度:=4 (分米)
放景观石后水面高度:=4.2 (分米)
景观石体积:(4.2- 4) ×8×3
=0.2×8×3
= 4.8 (立方分米)
答:这块景观石的体积是4.8立方分米。
【点睛】本题考查长方体的表面积和体积公式的实际应用、按比例分配,解答本题的关键是理解没放景观石前水面高度:=4 (分米),放景观石后水面高度:=4.2 (分米)。
19.100人
【分析】把六年级总人数看作单位“1”,育才小学六年级有的同学在扫地,有35人在擦玻璃,剩下的人数和六年级总人数的比是1∶4,则剩下的人数的分率为,则35人对应的分率为1--,运用除法即可求出六年级总人数。
【详解】35÷(1--)
=35÷
=100(人)
答:六年级共有学生100人。
【点睛】本题考查分数除法、比、分数减法,解答本题的关键是找准单位“1”,根据已知一个数的几分之几是多少,求这个数用除法计算即可。
20.300千米
【分析】根据题意得出:李龙比张勇晚了小时,则李龙比张勇多走了80×=60千米,又因为A城到C城与B城到C城的距离比是2∶3,则李龙比张勇多走的路程60千米占AB全程的,用除法解答即可。
【详解】80×÷
=60÷
=300(千米)
答:从城经城到城的路程是300千米。
【点睛】本题考查比的应用,解决本题关键是根据题意找出李龙多走的路程是全程的几分之几,用除法解答即可。
21.144只
【分析】开始缺席只数是出席只数的,缺席数量∶出席的数量,那么缺席的猴子数就是猴子总数的;同理后来缺席只数是出席只数的,缺席的猴子是猴子总数的,那么减少的分数对应的数量就2只,求总数用除法。
【详解】当缺席只数是出席只数的,缺席的猴子数就是猴子总数的;当缺席只数是出席只数的,缺席的猴子是猴子总数的;
,
(只)
答:这群猴子有144只。
【点评】本题考查分数除法的实际应用,解答本题的关键是理解不变的数量是猴子的总数,所以把猴子的总数看成单位“1”,分别找出两次缺席猴子数占总数的几分之几,再根据它们的差对应的数量是2,来求猴子总数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
