2015年浙江高考数学参考卷（理科）

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
2015年浙江省高考样卷数学(理科)
本试题卷分选择题和非选择题两部分。考试时间120分钟。
参考公式：
球的表面积公式S=4πR2球的体积公式V=πR3其中R表示球的半径锥体的体积公式V=Sh其中S表示锥体的底面积, h表示锥体的高 柱体的体积公式V=Sh其中S表示柱体的底面积, h表示柱体的高台体的体积公式其中S1, S2分别表示台体的上、下底面积, h表示台体的高
选择题部分
一、选择题
1．已知a，b是实数，则“| a＋b |＝| a |＋| b |”是“ab＞0”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
2．若函数f (x) (x∈R)是奇函数，则 （ ）
A．函数f (x2)是奇函数 B．函数 [f (x) ]2是奇函数
C．函数f (x) x2是奇函数 D．函数f (x)＋x2是奇函数3．若某几何体的三视图 (单位：cm) 如图所示，则此几何体的体积是 （ ）A． cm3 B． cm3 C． cm3 D． cm34．如图，在四边形ABCD中，AB⊥BC，AD⊥DC．若||＝a，||＝b，则＝ （ ）A．b2－a2 B．a2－b2 C．a2＋b2 D．ab5．现有90 kg货物需要装成5箱，要求每一箱所装货物的重量不超过其它任一箱所装货物重量的2倍．若某箱所装货物的重量为x kg，则x的取值范围是 （ ）A．10≤x≤18 B．10≤x≤30 C．18≤x≤30 D．15≤x≤30 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
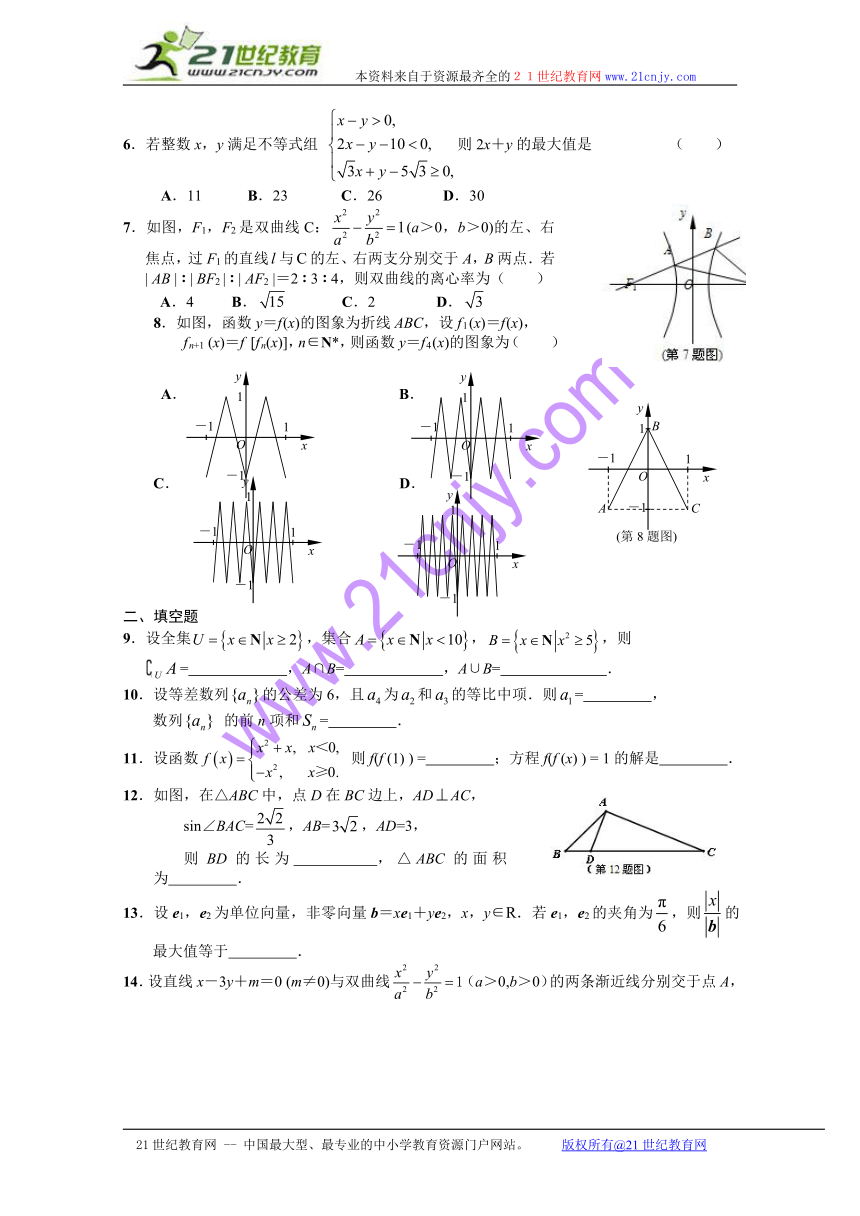
6．若整数x，y满足不等式组 则2x＋y的最大值是 （ ）
A．11 B．23 C．26 D．30
7．如图，F1，F2是双曲线C：(a＞0，b＞0)的左、右焦点，过F1的直线与的左、右两支分别交于A，B两点．若 | AB | : | BF2 | : | AF2 |＝2 : 3 : 4，则双曲线的离心率为（ ）A．4 B． C．2 D．8．如图，函数y＝f (x)的图象为折线ABC，设f 1 (x)＝f (x)，f n+1 (x)＝f [f n(x)]，n∈N*，则函数y＝f 4 (x)的图象为（ ） ( http: / / www.21cnjy.com )
A． B．
C． D．
二、填空题
9．设全集，集合，，则
= ，A∩B= ，A∪B= ．
10．设等差数列的公差为6，且为和的等比中项．则= ，
数列 的前n项和= ．
11．设函数 则f(f (1) ) = ；方程f(f (x) ) = 1的解是 ．
12．如图，在△ABC中，点D在BC边上，ADAC，sin∠BAC=，AB=，AD=3，则BD的长为 ，△ABC的面积为 ． ( http: / / www.21cnjy.com )
13．设e1，e2为单位向量，非零向量b＝xe1＋ye2，x，y∈R．若e1，e2的夹角为，则的最大值等于 ．21世纪教育网版权所有
14．设直线x－3y＋m＝0 (m≠0)与双曲线（a＞0,b＞0）的两条渐近线分别交于点A，B.若点P(m，0)满足，则该双曲线的离心率是 ．
15．如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小.若AB＝15m，AC＝25m，∠BCM＝30°，则tanθ的最大值是 ．(仰角θ为直线AP与平面ABC所成角) ( http: / / www.21cnjy.com )（第15题图）
三、解答题
16．已知函数f (x)＝3 sin2 ax＋sin ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
(Ⅰ) 求a的值；(Ⅱ) 求f (x)的值域．
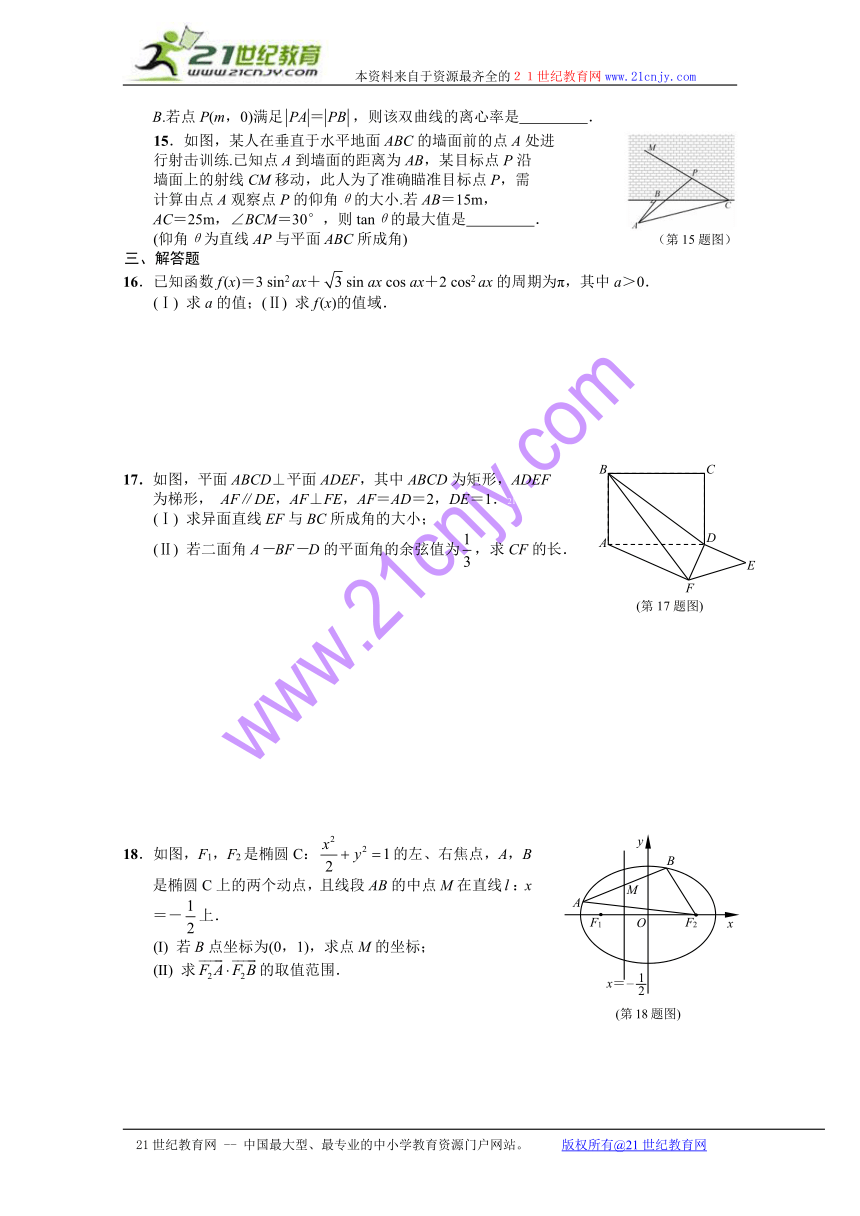
17．如图，平面ABCD⊥平面ADEF，其中ABCD为矩形，ADEF为梯形， AF∥DE，AF⊥FE，AF＝AD＝2，DE＝1．21教育网
(Ⅰ) 求异面直线EF与BC所成角的大小；
(Ⅱ) 若二面角A－BF－D的平面角的余弦值为，求CF的长．
18．如图，F1，F2是椭圆C：的左、右焦点，A，B是椭圆C上的两个动点，且线段AB的中点M在直线：x＝－上．21cnjy.com
(Ⅰ) 若B点坐标为(0，1)，求点M的坐标；
(Ⅱ) 求的取值范围．
19．设数列a1,a2,…,a2015满足性质P：
，．
(Ⅰ) (ⅰ) 若a1,a2,…,a2015是等差数列，求an；
(ⅱ) 是否存在具有性质P的等比数列a1,a2,…,a2015？
(Ⅱ) 求证：．
20．已知二次函数f (x) = ax2+bx+c (a>0)，方程f(x)－x=0的两个根x1，x2满足0（Ⅰ）当x(0, x1)时，证明x < f (x) < x1；
（Ⅱ）设函数f (x) 的图象关于直线x = x0对称，证明x0<．
数学参考试卷(理科)答案
一、选择题
1．B 2．C 3．D 4．A 5．B 6．B 7．A 8．D
二、填空题
9．，，
10．-14，3n2-17n 11．0， 12．，
13．2 14． 15．
三、解答题
16．(Ⅰ) 由题意得
f (x)＝(1－cos 2ax)＋sin 2ax＋(1＋cos 2ax)
＝sin 2ax－cos 2ax＋
＝sin (2ax－)＋．
因为f (x)的周期为π，a＞0，所以
a＝1．
(Ⅱ) 由(Ⅰ)得
f (x)＝sin (2x－)＋，
所以f (x)的值域为[，]．
17．(Ⅰ) 延长AD，FE交于Q．
因为ABCD是矩形，所以
BC∥AD，
所以∠AQF是异面直线EF与BC所成的角．
在梯形ADEF中，因为DE∥AF，AF⊥FE，AF＝2，DE＝1得
∠AQF＝30°．
(Ⅱ) 方法一：
设AB＝x．取AF的中点G．由题意得
DG⊥AF．
因为平面ABCD⊥平面ADEF，AB⊥AD，所以
AB⊥平面ADEF，
所以
AB⊥DG．
所以
DG⊥平面ABF．
过G作GH⊥BF，垂足为H，连结DH，则DH⊥BF，
所以∠DHG为二面角A－BF－D的平面角．
在直角△AGD中，AD＝2，AG＝1，得
DG＝．
在直角△BAF中，由＝sin∠AFB＝，得
＝，
所以
GH＝．
在直角△DGH中，DG＝，GH＝，得
DH＝．
因为cos∠DHG＝＝，x＝，
所以
AB＝．
又在梯形AFED中可得DF=2，
所以CF=．
方法二：设CD＝x．
以F为原点，AF，FQ所在的直线分别为x轴，y轴建立空间直角坐标系Fxyz．则
F(0，0，0)，A(－2，0，0)，E(，0，0)，D(－1，，0)，B(－2，0，x)，
所以
＝(1，－，0)，＝(2，0，－x)．
因为EF⊥平面ABF，所以平面ABF的法向量可取＝(0，1，0)．
设＝(x1，y1，z1)为平面BFD的法向量，则
所以，可取＝(，1，)．
因为cos<，>＝＝，得
x＝，
即
CD＝．
又在梯形AFED中可得DF=2，所以CF=.
18．(Ⅰ) 因为点M 是AB的中点，所以可设点A.
代入椭圆方程，得或，
则A点坐标为或，所以M点坐标为
或．
(Ⅱ) 当直线AB垂直于x轴时，直线AB方程为x＝－，此时
＝．
当直线AB不垂直于x轴时，设直线AB的斜率为k，M(－，m) (m≠0)，A(x1，y1)，B(x2，y2)．21·cn·jy·com
由 得
(x1＋x2)＋2(y1＋y2)＝0，
则
－1＋4mk＝0，
故
k＝．
此时，直线AB的方程为
y－m＝(x＋)，
即
y＝x＋．
联立 消去y，整理得
x2＋x＋ ＝0，
故Δ＝1－＞0，即
0＜m2＜，
所以
x1＋x2＝－1， x1x2＝．
于是
＝(x1－1)(x2－1)＋y1y2
＝x1x2＋y1y2－(x1＋x2)＋1
＝x1x2＋y1y2＋2
＝x1x2＋(x1＋)(x2＋)＋2
＝ ．
令t＝1＋8m2，则1＜t＜8，于是
＝
＝(3t＋)．
所以，的取值范围为[，）．
19．(Ⅰ) （ⅰ）设等差数列a1,a2,…,a2015的公差为d，则
．
由题意得
，
所以，即．
当d = 0时，a1=a2=…=a2015=0，所以与性质P矛盾；
当d > 0时，由，，得，．
所以
．
当时，由，，得，．
所以
．
综上所述，或．
（ⅱ）设a1,a2,…,a2015是公比为的等比数列，则
当时，，则
，
与性质P矛盾.
当时
.
与性质P矛盾.
因此不存在满足性质P的等比数列a1,a2,…,a2015．
(Ⅱ) 由条件知，必有ai > 0，也必有aj < 0 (i，j∈{1，2，…，2015}，且i≠j ) ．
设为所有ai中大于0的数，为所有ai中小于0的数．
由条件得a+a+…+a=，a+a+…+a= - ．所以
．
20． (Ⅰ)因为x1，x2是方程f (x) x =0的根，所以
f (x) x=a(x x1)(x x2) ．
当x∈(0，x1)时，由于x1< x2，a 0，所以 a(x x1)(x x2) 0，故
x < f (x) ．
因为x1 f (x)= x1 a(x x1)(x x2) x=(x1 x)[ 1+a(x x2)]，www.21-cn-jy.com
又 x1 x > 0，1+a(x x2) = 1+ax a x2 > 1 a x2> 0．于是
x1 f (x) > 0．
从而
f (x)< x1．
综上，x(Ⅱ)由题意知．
因为x1, x2是方程f (x) x = 0的根，即x1, x2是方程ax2+(b 1)x+c = 0的根，
所以
，
．
因为a x2<1，所以
．
O
x
y
1
1
－1
－1
O
x
y
1
1
－1
－1
A
B
C
O
x
y
1
1
－1
－1
(第8题图)
O
x
y
1
1
－1
－1
O
x
y
1
1
－1
－1
A
E
F
D
B
C
(第17题图)
O
B
A
x
y
x＝－
2
1
(第18题图)
M
F1
F2
A
E
F
D
B
C
(第17题图)
H
G
Q
A
E
F
D
B
C
(第17题图)
x
z
y
O
B
A
x
y
x＝－
2
1
(第18题图)
M
F1
F2
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网