4.4.1对数函数的概念 课件(共21张PPT) 人教A版(2019)必修第一册
文档属性
| 名称 | 4.4.1对数函数的概念 课件(共21张PPT) 人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 29.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 09:29:18 | ||
图片预览







文档简介
(共21张PPT)
对数函数
对数函数的概念
对数函数的图象和性质
对数函数及其性质的应用
2026届
高一
数学
路径:
概念
背景
图象及其性质
应用
4.4 对数
4.4.1对数函数的概念
2026届
高一
数学
学习目标
知 识 目 标 学 科 素 养
1.理解对数函数的概念, 2.会求对数函数的定义域.(重点、难点) 1、数学抽象
2、逻辑推理
2026届
高一
数学
对中科院古脊椎动物与古人类研究所的专家向外界确认,河南汝阳村李锤发现的“龙骨”实际上是一头距今已有1亿至8 000万年历史的黄河巨龙的肋骨.经过发掘、整理、还原模型,专家推断这条黄河巨龙活着的时候,体重应该在60吨左右,是迄今为止亚洲最高大、最肥胖的“亚洲龙王”.
探究
?
【想一想】
同学们知道专家是怎样依据“龙骨”化石估算出黄河巨龙的生活年代的吗?
2026届
高一
数学
在4.2.1的问题2中,我们已经研究了死亡生物体内碳14的含量 y 随死亡时间x的变化而衰减的规律. 反过来,已知死亡生物体内碳14的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间 x 是碳14的含量y的函数吗?
思考1
?
2026届
高一
数学
设生物死亡年数为 x,死亡生物体内碳14含量为 y .
指数函数模型研究了呈指数增长或衰减变化规律的问题.
2026届
高一
数学
设生物死亡年数为 x,死亡生物体内碳14含量为 y .
问题1 由死亡生物体内碳14含量,如何求出它的死亡年数呢?
指数函数
对数函数
2026届
高一
数学
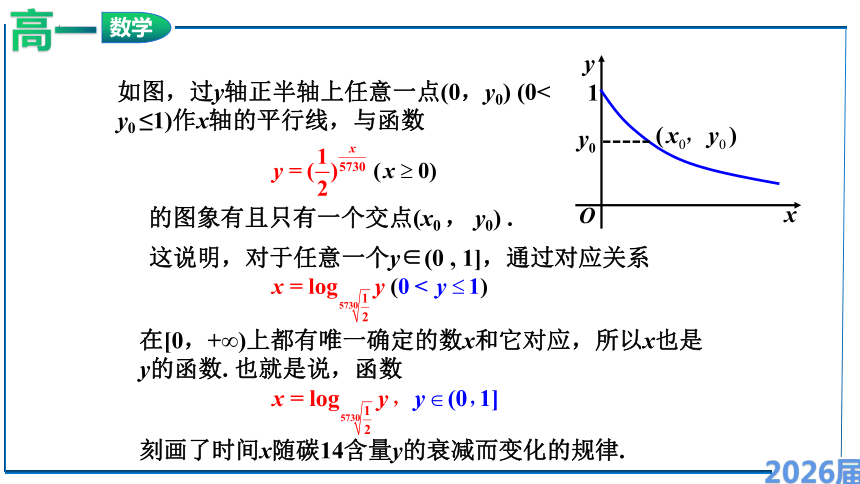
如图,过y轴正半轴上任意一点(0,y0) (0< y0 ≤1)作x轴的平行线,与函数
的图象有且只有一个交点(x0 , y0) .
这说明,对于任意一个y∈(0 , 1],通过对应关系
在[0,+∞)上都有唯一确定的数x和它对应,所以x也是y的函数. 也就是说,函数
刻画了时间x随碳14含量y的衰减而变化的规律.
2026届
高一
数学
同样地,根据指数与对数的关系,由
y=ax(a>0且a≠1)
可以得到
x=loga y(a>0且a≠1),
x也是y的函数. 通常,我们用x表示自变量,y表示函数.
为此,将x=loga y(a>0且a≠1)中的字母x和y对调,写成
y=loga x (a>0且a≠1).
2026届
高一
数学
对数函数的概念
定义:一般地,函数y=logax(a>0,且a≠1)叫做
对数函数,其中x是自变量,定义域是(0,+∞).
对数函数的特征:
1.底数:a>0,且a≠1
2.真数:自变量 x
3.系数:1
2026届
高一
数学
概念理解
判断下列函数是不是对数函数
不是
不是
不是
是
是
2026届
高一
数学
变式 给出下列函数:
①y=log2(3x-2); ②y=2log0.3x; ③y=log(x-1)x;
④y=lgx; ⑤y=log3x; ⑥y=lnx.
其中所有对数函数的序号是( )
A.①②⑤ B.④⑤⑥ C.①②④⑤⑥ D.③④
B
2026届
高一
数学
判断一个函数是对数的依据:
(1)形式:形如;
(2)系数:对数符号前面的系数为1;
(3)底数:底数为大于0且不等于1的常数;
(4)对数的真数仅有自变量
2026届
高一
数学
变式2 函数是对数函数,则函数
答案:
(2)∵,解得或-3.
而∴.即
∴
2026届
高一
数学
对数函数的定义域
例2 求下列函数的定义域:
(1) y=log3x2 (2) y=loga(4-x) (a>0,且a≠1)
解:(1)因为x2>0,即x≠0,
所以函数 y=log3x2 的定义域是{x|x≠0}
(2)因为4-x>0,即x<4,
所以函数 y=loga(4-x) 的定义域是{x|x<4}.
2026届
高一
数学
求对数型函数定义域的原则:
(1)分母不能为0;
(2)根指数为偶数时,被开方数非负;
(3)对数的真数大于0,底数大于0且不为1;
(4)若需对函数进行变形,则需先求出定义域,再对函数进行恒等变形.
2026届
高一
数学
当堂练习
1.求下列函数的定义域:
(1)y=ln(1-x); (2);
(3); (4)y=loga|x|(a>0,且a≠1)
2026届
高一
数学
当堂练习
1.求下列函数的定义域:
(1)y=ln(1-x); (2);
(3); (4)y=loga|x|(a>0,且a≠1)
2026届
高一
数学
变式2 求下列函数的定义域.
(1)(2)(3)
答案:(1)由 得
∴定义域为
(2)由得.由指数函数的单调性知,
∴定义域为
(3)据题意得:且,得且
∴定义域为
2026届
高一
数学
(4) (5) (6)
答案:(4)由 得且
∴定义域为
(5)由得.即
∴定义域为
(6)据题意得:且,得且
而即
∴定义域为
2026届
高一
数学
课堂小结
对数函数:一般地,函数y=logax(a>0,且a≠1)叫做
对数函数,其中x是自变量,定义域是(0,+∞).
对数函数的特征:
1.底数:a>0,且a≠1
2.真数:自变量 x
3.系数:1
2026届
高一
数学
对数函数
对数函数的概念
对数函数的图象和性质
对数函数及其性质的应用
2026届
高一
数学
路径:
概念
背景
图象及其性质
应用
4.4 对数
4.4.1对数函数的概念
2026届
高一
数学
学习目标
知 识 目 标 学 科 素 养
1.理解对数函数的概念, 2.会求对数函数的定义域.(重点、难点) 1、数学抽象
2、逻辑推理
2026届
高一
数学
对中科院古脊椎动物与古人类研究所的专家向外界确认,河南汝阳村李锤发现的“龙骨”实际上是一头距今已有1亿至8 000万年历史的黄河巨龙的肋骨.经过发掘、整理、还原模型,专家推断这条黄河巨龙活着的时候,体重应该在60吨左右,是迄今为止亚洲最高大、最肥胖的“亚洲龙王”.
探究
?
【想一想】
同学们知道专家是怎样依据“龙骨”化石估算出黄河巨龙的生活年代的吗?
2026届
高一
数学
在4.2.1的问题2中,我们已经研究了死亡生物体内碳14的含量 y 随死亡时间x的变化而衰减的规律. 反过来,已知死亡生物体内碳14的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间 x 是碳14的含量y的函数吗?
思考1
?
2026届
高一
数学
设生物死亡年数为 x,死亡生物体内碳14含量为 y .
指数函数模型研究了呈指数增长或衰减变化规律的问题.
2026届
高一
数学
设生物死亡年数为 x,死亡生物体内碳14含量为 y .
问题1 由死亡生物体内碳14含量,如何求出它的死亡年数呢?
指数函数
对数函数
2026届
高一
数学
如图,过y轴正半轴上任意一点(0,y0) (0< y0 ≤1)作x轴的平行线,与函数
的图象有且只有一个交点(x0 , y0) .
这说明,对于任意一个y∈(0 , 1],通过对应关系
在[0,+∞)上都有唯一确定的数x和它对应,所以x也是y的函数. 也就是说,函数
刻画了时间x随碳14含量y的衰减而变化的规律.
2026届
高一
数学
同样地,根据指数与对数的关系,由
y=ax(a>0且a≠1)
可以得到
x=loga y(a>0且a≠1),
x也是y的函数. 通常,我们用x表示自变量,y表示函数.
为此,将x=loga y(a>0且a≠1)中的字母x和y对调,写成
y=loga x (a>0且a≠1).
2026届
高一
数学
对数函数的概念
定义:一般地,函数y=logax(a>0,且a≠1)叫做
对数函数,其中x是自变量,定义域是(0,+∞).
对数函数的特征:
1.底数:a>0,且a≠1
2.真数:自变量 x
3.系数:1
2026届
高一
数学
概念理解
判断下列函数是不是对数函数
不是
不是
不是
是
是
2026届
高一
数学
变式 给出下列函数:
①y=log2(3x-2); ②y=2log0.3x; ③y=log(x-1)x;
④y=lgx; ⑤y=log3x; ⑥y=lnx.
其中所有对数函数的序号是( )
A.①②⑤ B.④⑤⑥ C.①②④⑤⑥ D.③④
B
2026届
高一
数学
判断一个函数是对数的依据:
(1)形式:形如;
(2)系数:对数符号前面的系数为1;
(3)底数:底数为大于0且不等于1的常数;
(4)对数的真数仅有自变量
2026届
高一
数学
变式2 函数是对数函数,则函数
答案:
(2)∵,解得或-3.
而∴.即
∴
2026届
高一
数学
对数函数的定义域
例2 求下列函数的定义域:
(1) y=log3x2 (2) y=loga(4-x) (a>0,且a≠1)
解:(1)因为x2>0,即x≠0,
所以函数 y=log3x2 的定义域是{x|x≠0}
(2)因为4-x>0,即x<4,
所以函数 y=loga(4-x) 的定义域是{x|x<4}.
2026届
高一
数学
求对数型函数定义域的原则:
(1)分母不能为0;
(2)根指数为偶数时,被开方数非负;
(3)对数的真数大于0,底数大于0且不为1;
(4)若需对函数进行变形,则需先求出定义域,再对函数进行恒等变形.
2026届
高一
数学
当堂练习
1.求下列函数的定义域:
(1)y=ln(1-x); (2);
(3); (4)y=loga|x|(a>0,且a≠1)
2026届
高一
数学
当堂练习
1.求下列函数的定义域:
(1)y=ln(1-x); (2);
(3); (4)y=loga|x|(a>0,且a≠1)
2026届
高一
数学
变式2 求下列函数的定义域.
(1)(2)(3)
答案:(1)由 得
∴定义域为
(2)由得.由指数函数的单调性知,
∴定义域为
(3)据题意得:且,得且
∴定义域为
2026届
高一
数学
(4) (5) (6)
答案:(4)由 得且
∴定义域为
(5)由得.即
∴定义域为
(6)据题意得:且,得且
而即
∴定义域为
2026届
高一
数学
课堂小结
对数函数:一般地,函数y=logax(a>0,且a≠1)叫做
对数函数,其中x是自变量,定义域是(0,+∞).
对数函数的特征:
1.底数:a>0,且a≠1
2.真数:自变量 x
3.系数:1
2026届
高一
数学
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
