24.1.2垂直于弦的直径 同步练习(含答案) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1.2垂直于弦的直径 同步练习(含答案) 2023-2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 462.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 09:28:11 | ||
图片预览


文档简介
24.1.2垂直于弦的直径
一、单选题
1.P为⊙O内一点,,⊙O半径为5,则经过P点的最短弦长为( )
A.5 B.6 C.8 D.10
2.已知的直径为10cm, ,是的两条弦,,,,则与之间的距离为( ).
A.1 B.7 C.1或7 D.3或4
3.如图,BC为⊙O直径,交弦AD于点E,若B点为中点,则说法错误的是( )
A.AD⊥BC B. C.AE=DE D.OE=BE
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是( )
A.2.5 B.3 C.3.5 D.4
5.如图⊙O的直径垂直于弦,垂足是,,,的长为( )
A. B.4 C. D.8
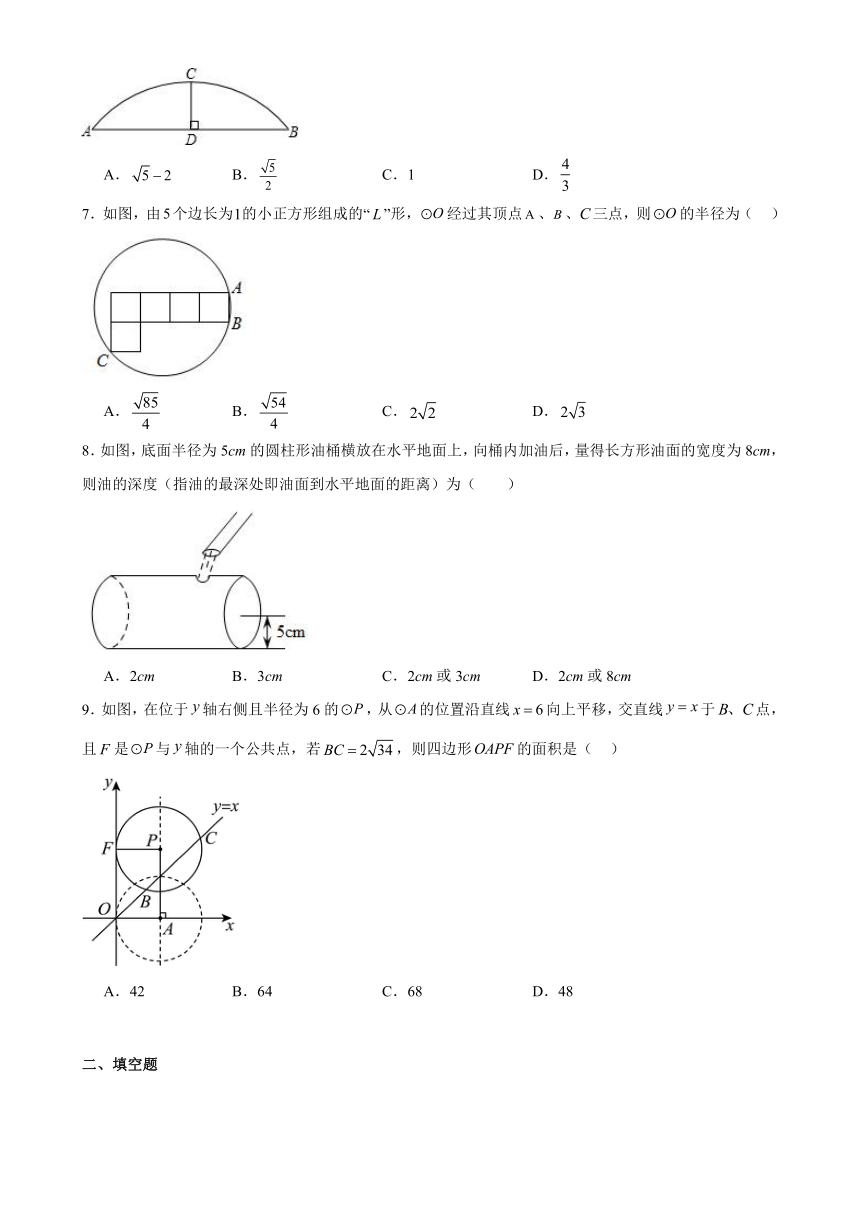
6.一种花边由如图的弓形组成,弧ACB的半径为,弦AB=2,则弓形的高CD为( )
A. B. C.1 D.
7.如图,由个边长为的小正方形组成的“”形,经过其顶点、、三点,则的半径为( )
A. B. C. D.
8.如图,底面半径为5cm的圆柱形油桶横放在水平地面上,向桶内加油后,量得长方形油面的宽度为8cm,则油的深度(指油的最深处即油面到水平地面的距离)为( )
A.2cm B.3cm C.2cm或3cm D.2cm或8cm
9.如图,在位于轴右侧且半径为6的,从的位置沿直线向上平移,交直线于点,且是与轴的一个公共点,若,则四边形的面积是( )
A.42 B.64 C.68 D.48
二、填空题
10.已知圆心到圆的两条平行弦的距离分别是2和3,则两条平行弦之间的距离为 .
11.如图,的半径垂直于弦于点,连结并延长交于点,连结.若,则的长为 .
12.已知:如图,⊙C与坐标轴交于A(1,0)、B(5,0)两点,⊙C的半径为3,则圆心C的坐标为 .
13.如图,是一个油罐的截面图.已知的直径为10m,油的最大深度,则油面宽度为 m.
14.《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深1寸,锯道尺(1尺=10寸),则该圆材的直径为 寸.
15.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章关于计算弧田面积所用的公式如下:弧田面积=(弦×矢+矢×矢).弧田(图中的阴影部分)由圆弧和其所对的弦围成.公式中的“弦”是指圆弧所对的弦长.“矢”等于半径长与圆心到弦的距离之差.现已知弦AB=24米.半径OA=15米的弧田,按照上述公式计算出弧田的面积为 平方米.
三、解答题
16.如图,AB为⊙O的直径,点D在⊙O上,∠BAD=36°,点C为弧AD的中点,连接OC,AC.
(1)补全图形,并写出作图的方法或依据;
(2)求∠ACO的度数.
17.如图,AB是⊙O的直径,点C、D是圆上两点,且OD∥AC,OD与BC交于点E.
(1)求证:E为BC的中点;
(2)若BC=8,DE=3,求AB的长度.
18.如图,AB是的直径,于点E,连接CO并延长交AD于点F,且.
(1)求证:E是OB的中点;
(2)若,求CD的长.
19.如图1是博物馆展出的古代车轮实物,《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸……”据此,我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A,B两点,设所在圆的圆心为O,半径为.
作弦AB的垂线OC,D为垂足,则___________.
经测量,,则___________;用含r的代数式表示___________.
在中,由勾股定理可列出关于r的方程:___________.解得.
通过换算,车轮直径约为六尺六寸,可验证此车轮为___________之轮.(填“兵车”或“田车”)
参考答案:
1.C
2.C
3.D
4.B
5.C
6.A
7.A
8.D
9.D
10.1或5.
11.
12.
13.8
14.26
15.90
16.63°.
17..
18.
19.,,,,兵车
一、单选题
1.P为⊙O内一点,,⊙O半径为5,则经过P点的最短弦长为( )
A.5 B.6 C.8 D.10
2.已知的直径为10cm, ,是的两条弦,,,,则与之间的距离为( ).
A.1 B.7 C.1或7 D.3或4
3.如图,BC为⊙O直径,交弦AD于点E,若B点为中点,则说法错误的是( )
A.AD⊥BC B. C.AE=DE D.OE=BE
4.如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),则OP的最小值是( )
A.2.5 B.3 C.3.5 D.4
5.如图⊙O的直径垂直于弦,垂足是,,,的长为( )
A. B.4 C. D.8
6.一种花边由如图的弓形组成,弧ACB的半径为,弦AB=2,则弓形的高CD为( )
A. B. C.1 D.
7.如图,由个边长为的小正方形组成的“”形,经过其顶点、、三点,则的半径为( )
A. B. C. D.
8.如图,底面半径为5cm的圆柱形油桶横放在水平地面上,向桶内加油后,量得长方形油面的宽度为8cm,则油的深度(指油的最深处即油面到水平地面的距离)为( )
A.2cm B.3cm C.2cm或3cm D.2cm或8cm
9.如图,在位于轴右侧且半径为6的,从的位置沿直线向上平移,交直线于点,且是与轴的一个公共点,若,则四边形的面积是( )
A.42 B.64 C.68 D.48
二、填空题
10.已知圆心到圆的两条平行弦的距离分别是2和3,则两条平行弦之间的距离为 .
11.如图,的半径垂直于弦于点,连结并延长交于点,连结.若,则的长为 .
12.已知:如图,⊙C与坐标轴交于A(1,0)、B(5,0)两点,⊙C的半径为3,则圆心C的坐标为 .
13.如图,是一个油罐的截面图.已知的直径为10m,油的最大深度,则油面宽度为 m.
14.《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深1寸,锯道尺(1尺=10寸),则该圆材的直径为 寸.
15.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章关于计算弧田面积所用的公式如下:弧田面积=(弦×矢+矢×矢).弧田(图中的阴影部分)由圆弧和其所对的弦围成.公式中的“弦”是指圆弧所对的弦长.“矢”等于半径长与圆心到弦的距离之差.现已知弦AB=24米.半径OA=15米的弧田,按照上述公式计算出弧田的面积为 平方米.
三、解答题
16.如图,AB为⊙O的直径,点D在⊙O上,∠BAD=36°,点C为弧AD的中点,连接OC,AC.
(1)补全图形,并写出作图的方法或依据;
(2)求∠ACO的度数.
17.如图,AB是⊙O的直径,点C、D是圆上两点,且OD∥AC,OD与BC交于点E.
(1)求证:E为BC的中点;
(2)若BC=8,DE=3,求AB的长度.
18.如图,AB是的直径,于点E,连接CO并延长交AD于点F,且.
(1)求证:E是OB的中点;
(2)若,求CD的长.
19.如图1是博物馆展出的古代车轮实物,《周礼·考工记》记载:“……故兵车之轮六尺有六寸,田车之轮六尺有三寸……”据此,我们可以通过计算车轮的半径来验证车轮类型,请将以下推理过程补充完整.
如图2所示,在车轮上取A,B两点,设所在圆的圆心为O,半径为.
作弦AB的垂线OC,D为垂足,则___________.
经测量,,则___________;用含r的代数式表示___________.
在中,由勾股定理可列出关于r的方程:___________.解得.
通过换算,车轮直径约为六尺六寸,可验证此车轮为___________之轮.(填“兵车”或“田车”)
参考答案:
1.C
2.C
3.D
4.B
5.C
6.A
7.A
8.D
9.D
10.1或5.
11.
12.
13.8
14.26
15.90
16.63°.
17..
18.
19.,,,,兵车
同课章节目录
