第11章三角形 期末综合复习训练题(含答案) 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 第11章三角形 期末综合复习训练题(含答案) 2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 136.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 09:35:12 | ||
图片预览




文档简介
2023-2024学年人教版八年级数学上册《第11章三角形》期末综合复习训练题(附答案)
一、选择题
1.三角形的三条高线的交点在三角形的一个顶点上,则此三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰三角形
2.如图,点D,E,F分别是AB,CA上的点,且AE,CD交于点O,它们将△ABC分成6个面积相等的三角形,BF,CD一定是△ABC的( )
A.高 B.中线
C.角平分线 D.三边的垂直平分线
3.三条线段a=5,b=3,c的值为奇数,b,c为边可组成三角形( )
A.1个 B.3个 C.5个 D.无数个
4.如图,AD是△ABC的中线,已知△ABD的周长为25cm,则△ACD的周长( )
A.18cm B.22cm C.19cm D.31cm
5.若一个正多边形的内角和为720°,则这个正多边形的每一个内角是( )
A.60° B.90° C.108° D.120°
6.满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=2:3:5
C.∠A=2∠B=3∠C D.一个外角等于和它相邻的一个内角
7.如图,m∥n,直线l分别交m,点B,AC⊥AB,若∠1=35°,则∠2等于( )
A.35° B.45° C.55° D.65°
8.如图所示,在△ABC中,D在AC上,且∠ABC=∠C=∠1,∠A=∠3( )
A.30° B.36° C.45° D.72°
9.将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
10.如图,已知四边形ABCD,∠α,∠BCD相邻的补角,且∠B+∠ADC=140°( )
A.140° B.170° C.260° D.120°
二、填空题
11.电工师傅在安好电线杆后,为了防止电线杆倾倒,常常按图所示引两条拉线 .
12.等腰三角形的两边的边长分别为20cm和9cm,则第三边的长是 .
13.在△ABC中,∠A:∠B:∠C=2:3:4,则∠A= ,∠C= .
14.如图,在△ABC中,AD⊥BC于D,∠B=80°,∠C=46° .
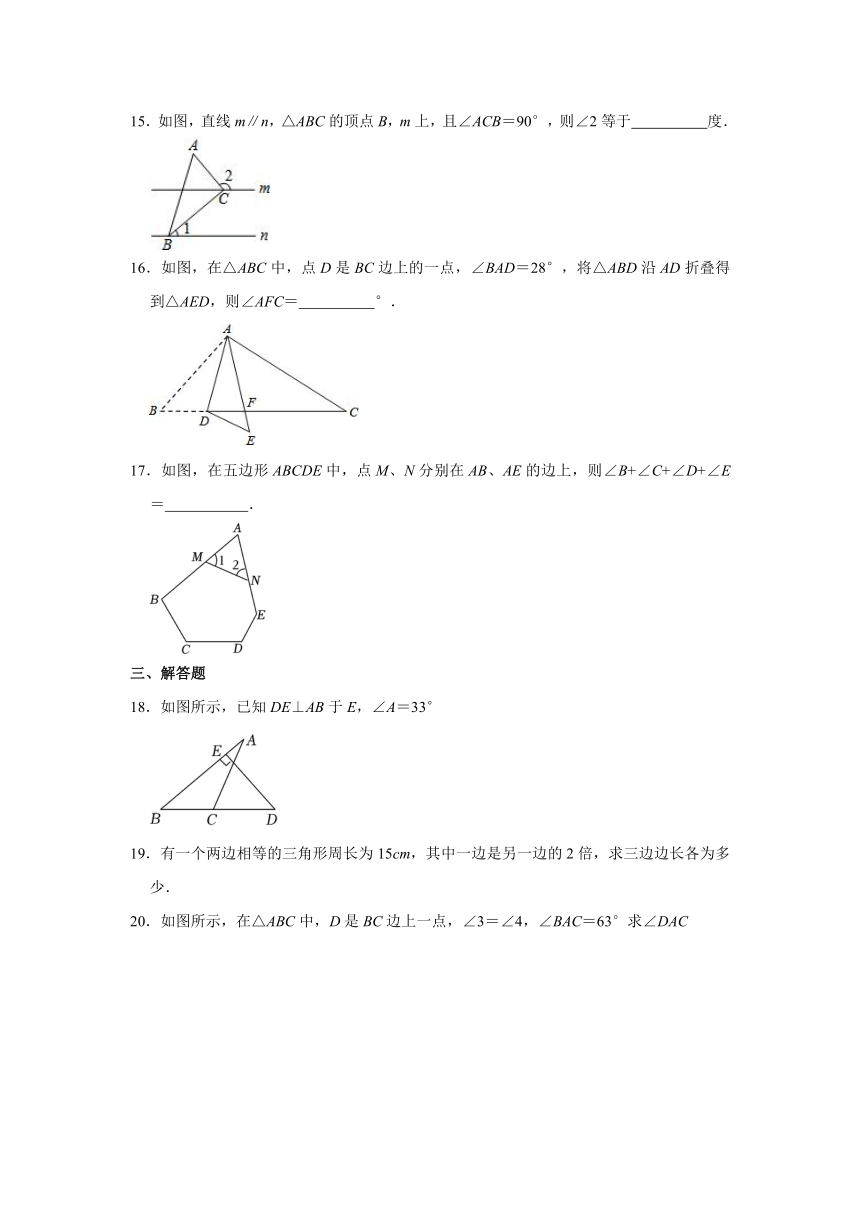
15.如图,直线m∥n,△ABC的顶点B,m上,且∠ACB=90°,则∠2等于 度.
16.如图,在△ABC中,点D是BC边上的一点,∠BAD=28°,将△ABD沿AD折叠得到△AED,则∠AFC= °.
17.如图,在五边形ABCDE中,点M、N分别在AB、AE的边上,则∠B+∠C+∠D+∠E= .
三、解答题
18.如图所示,已知DE⊥AB于E,∠A=33°
19.有一个两边相等的三角形周长为15cm,其中一边是另一边的2倍,求三边边长各为多少.
20.如图所示,在△ABC中,D是BC边上一点,∠3=∠4,∠BAC=63°求∠DAC
21.如图,七边形ABCDEFG中、AB,ED的延长线相交于点O.若图中∠1,∠3,∠4的外角的角度和为220°
22.如图,△ABC中,∠ABC=40°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
23.如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF.
(1)求∠ECF+DAC+∠ECA的度数;
(2)判断ED与FC的位置关系,并对你的结论加以证明.
24.如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,∠D=β.
(1)如图①,α+β>180°,试用α;
(2)如图②,α+β<180°,请在图中画出∠F,β表示∠F;
(3)一定存在∠F吗?如有,求出∠F的值,如不一定,β满足什么条件时,不存在∠
F.
参考答案
一、选择题
1.解:∵三角形的三条高线的交点在三角形的一个顶点上,
∴此三角形是直角三角形.
故选:A.
2.解:∵S△OAD=S△OBD,
∴AD=BD,
∴CD是△ABC的中线,
同理,BF,
故选:B.
3.解:根据三角形的三边关系知c的取值范围是:2<c<8,
又c的值为奇数,
因而c的值可以是:3、5、7共5个数,
因而由a、b、c为边可组成3个三角形.
故选:B.
4.解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC,
∵△ABD的周长为25cm,AB比AC长7cm,
∴△ACD周长为:25﹣7=18(cm).
故选:A.
5.解:(n﹣2)×180°=720°,
∴n﹣2=4,
∴n=6.
则这个正多边形的每一个内角为720°÷6=120°.
故选:D.
6.解:A.∵∠A+∠B=∠C,
∴三角形中最大角∠C=×180°=90°,
∴满足条件的三角形为直角三角形,选项A不符合题意;
B.∵∠A:∠B:∠C=3:3:5,
∴三角形中最大角∠C=×180°=90°,
∴满足条件的三角形为直角三角形,选项B不符合题意;
C.∵∠A=2∠B=3∠C,
∴∠A=,,∠C=,
∴选项C符合题意
D.∵一个外角等于和它相邻的一个内角,
∴该内角=×180°=90°,
∴满足条件的三角形为直角三角形,选项D不符合题意.
故选:C.
7.解:如图,
∵AC⊥AB,
∴∠3+∠1=90°,
∴∠8=90°﹣∠1=90°﹣35°=55°,
∵直线m∥n,
∴∠3=∠8=55°,
故选:C.
8.解:设∠A=∠3=x°,
则∠1=∠A+∠8=2x°,
∵∠ABC=∠C=∠1,
∴∠ABC=∠C=∠5=2x°,
∵∠A+∠ABC+∠C=180°,
∴x+2x+7x=180,
∴x=36,
∴∠A=36°,
故选:B.
9.解:∵图中是一副直角三角板,
∴∠A=30°,∠DCE=45°,
∴∠ACD=135°,
∴α=30°+135°=165°.
故选:A.
10.解:∵∠B+∠D+∠DAB+∠BCD=360°,∠B+∠ADC=140°,
∴∠DAB+∠BCD=360°﹣140°=220°,
∵∠α+∠β+∠DAB+∠BCD=360°,
∴∠α+∠β=360°﹣220°=140°,
故选:A.
二、填空题
11.解:结合图形,为了防止电线杆倾倒,两条拉线与地面就构成了三角形.
故答案为:三角形的稳定性.
12.解:①当20cm为底边时,第三边长为9cm,故不能构成三角形;
②当9cm为底边时,第三边长为20cm,故能构成三角形;
故答案为:20cm.
13.解:设∠A=2x°,则∠B=3x°,
∵∠A+∠B+∠C=180°,
即:2x°+3x°+4x°=180°,
解得:x=20
∴∠A=40°,则∠B=60°,
故答案为:40°、80°
14.解:∵在△ABC中,AD⊥BC于D,∠B=80°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣80°﹣46°=54°,
∴∠BAE=∠CAE==27°,
∵∠B=80°,AD⊥BC,
∴∠ADB=90°,
∴∠BAD=10°,
∴∠DAE=∠BAE﹣∠BAD=27°﹣10°=17°,
故答案为:17°.
15.解:∵m∥n,∠1=40°,
∴∠3=∠5=40°.
∵∠ACB=90°,
∴∠4=∠ACB﹣∠3=90°﹣40°=50°,
∴∠5=180°﹣∠4=180°﹣50°=130°.
故答案为:130.
16.解:∵∠BAD=28°,将△ABD沿AD折叠得到△AED,
∴∠BAD=∠FAD=28°,
∵∠B=48°,
∴∠ADF=∠B+∠BAD=48°+28°=76°,
∴∠AFC=∠FAD+∠ADF=28°+76°=104°,
故答案为:104.
17.解:∵∠1+∠2=120°,∠4+∠2+∠A=180°,
∴∠A=180°﹣(∠1+∠2)=60°,
∵五边形ABCDE的内角和为:(5﹣2)×180°=540°,
∴∠B+∠C+∠D+∠E=540°﹣∠A=540°﹣60°=480°,
故答案为:480°.
三、解答题
18.解:∠B=180°﹣∠BED﹣∠D
=180°﹣90°﹣50°
=40°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣33°﹣40°=107°.
19.解:设一边是2xcm,另一边为xcm,
根据题意,分情况讨论:
①以xcm为底边,
则2x+2x+x=15,
解得x=3,
∴2×4=6(cm),
∴三边长为6cm,5cm;
②以xcm为腰长,
根据三角形的三边关系,不能构成三角形,
综上所述,三边长为6cm,3cm.
20.解:设∠1=∠2=x,则∠4=∠4=2x.
因为∠BAC=63°,
所以∠5+∠4=117°,即x+2x=117°,
所以x=39°;
所以∠8=∠4=78°,
∠DAC=180°﹣∠3﹣∠7=24°.
21.解:五边形AOEFG的外角和为360°,
∵∠1,∠2,∠7的外角的角度和为220°,
∴∠AOE的外角为360°﹣220°=140°,
∵∠AOE=180°﹣140°=40°.
∴∠BOD=40°.
22.解:(1)∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∵∠ABC=40°,∠C=60°,
∴∠BAD=50°,∠CAD=30°,
∴∠BAC=50°+30°=80°,
∵AE是∠BAC的平分线,
∴∠BAE=40°,
∴∠DAE=50°﹣40°=10°.
(2)AD是△ABE、△ABD、△AED、△ADC的高.
23.解:(1)∵∠ECF=∠ECB+∠BCF,
∴∠ECF+∠DAC+∠ECA
=(∠ECB+∠BCF)+∠DAC+∠ECA (∠BCF=∠BAD)
=(∠ECB+∠ECA)+(∠DAC+∠BAD)
=∠BCA+∠BAC
=45°+45°
=90°
即∠ECF+DAC+∠ECA=90°;
(2)ED和FC平行,理由如下:
∵∠EAD=∠AED=45°,
∴∠EDA=90°,
∴在C,E,D,A四点组成的凹四边形里,
∠ECA+∠CED+∠CAD=∠EDA=90°
又∵(1)的结论是∠ECF+DAC+∠ECA=90°,
∴∠CED=∠ECF,
∴DE∥CF(内错角相等,两直线平行).
24.解:(1)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠FBC+(180°﹣2∠DCF)=180°﹣8(∠DCF﹣∠FBC)=180°﹣2∠F,
∴360°﹣(α+β)=180°﹣2∠F,
7∠F=α+β﹣180°,
∴∠F=(α+β)﹣90°;
(2)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=8∠GBC+(180°﹣2∠HCE)=180°+2(∠GBC﹣∠HCE)=180°+2∠F,
∴360°﹣(α+β)=180°+2∠F,
∠F=90°﹣(α+β);
(3)当α+β=180°时,不存在∠F,
∵α+β=180°,
∴AB∥CD,
∴∠ABC的角平分线及外角∠DCE的平分线平行,
∴∠F不存在,
∴当α+β=180°时,不存在∠F.
一、选择题
1.三角形的三条高线的交点在三角形的一个顶点上,则此三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等腰三角形
2.如图,点D,E,F分别是AB,CA上的点,且AE,CD交于点O,它们将△ABC分成6个面积相等的三角形,BF,CD一定是△ABC的( )
A.高 B.中线
C.角平分线 D.三边的垂直平分线
3.三条线段a=5,b=3,c的值为奇数,b,c为边可组成三角形( )
A.1个 B.3个 C.5个 D.无数个
4.如图,AD是△ABC的中线,已知△ABD的周长为25cm,则△ACD的周长( )
A.18cm B.22cm C.19cm D.31cm
5.若一个正多边形的内角和为720°,则这个正多边形的每一个内角是( )
A.60° B.90° C.108° D.120°
6.满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A:∠B:∠C=2:3:5
C.∠A=2∠B=3∠C D.一个外角等于和它相邻的一个内角
7.如图,m∥n,直线l分别交m,点B,AC⊥AB,若∠1=35°,则∠2等于( )
A.35° B.45° C.55° D.65°
8.如图所示,在△ABC中,D在AC上,且∠ABC=∠C=∠1,∠A=∠3( )
A.30° B.36° C.45° D.72°
9.将一副直角三角板按如图方式叠放在一起,则∠α的度数是( )
A.165° B.120° C.150° D.135°
10.如图,已知四边形ABCD,∠α,∠BCD相邻的补角,且∠B+∠ADC=140°( )
A.140° B.170° C.260° D.120°
二、填空题
11.电工师傅在安好电线杆后,为了防止电线杆倾倒,常常按图所示引两条拉线 .
12.等腰三角形的两边的边长分别为20cm和9cm,则第三边的长是 .
13.在△ABC中,∠A:∠B:∠C=2:3:4,则∠A= ,∠C= .
14.如图,在△ABC中,AD⊥BC于D,∠B=80°,∠C=46° .
15.如图,直线m∥n,△ABC的顶点B,m上,且∠ACB=90°,则∠2等于 度.
16.如图,在△ABC中,点D是BC边上的一点,∠BAD=28°,将△ABD沿AD折叠得到△AED,则∠AFC= °.
17.如图,在五边形ABCDE中,点M、N分别在AB、AE的边上,则∠B+∠C+∠D+∠E= .
三、解答题
18.如图所示,已知DE⊥AB于E,∠A=33°
19.有一个两边相等的三角形周长为15cm,其中一边是另一边的2倍,求三边边长各为多少.
20.如图所示,在△ABC中,D是BC边上一点,∠3=∠4,∠BAC=63°求∠DAC
21.如图,七边形ABCDEFG中、AB,ED的延长线相交于点O.若图中∠1,∠3,∠4的外角的角度和为220°
22.如图,△ABC中,∠ABC=40°,AD⊥BC于D,AE是∠BAC的平分线.
(1)求∠DAE的度数;
(2)指出AD是哪几个三角形的高.
23.如图,△ADE和△ABC中∠EAD=∠AED=∠BAC=∠BCA=45°,又有∠BAD=∠BCF.
(1)求∠ECF+DAC+∠ECA的度数;
(2)判断ED与FC的位置关系,并对你的结论加以证明.
24.如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,∠D=β.
(1)如图①,α+β>180°,试用α;
(2)如图②,α+β<180°,请在图中画出∠F,β表示∠F;
(3)一定存在∠F吗?如有,求出∠F的值,如不一定,β满足什么条件时,不存在∠
F.
参考答案
一、选择题
1.解:∵三角形的三条高线的交点在三角形的一个顶点上,
∴此三角形是直角三角形.
故选:A.
2.解:∵S△OAD=S△OBD,
∴AD=BD,
∴CD是△ABC的中线,
同理,BF,
故选:B.
3.解:根据三角形的三边关系知c的取值范围是:2<c<8,
又c的值为奇数,
因而c的值可以是:3、5、7共5个数,
因而由a、b、c为边可组成3个三角形.
故选:B.
4.解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC,
∵△ABD的周长为25cm,AB比AC长7cm,
∴△ACD周长为:25﹣7=18(cm).
故选:A.
5.解:(n﹣2)×180°=720°,
∴n﹣2=4,
∴n=6.
则这个正多边形的每一个内角为720°÷6=120°.
故选:D.
6.解:A.∵∠A+∠B=∠C,
∴三角形中最大角∠C=×180°=90°,
∴满足条件的三角形为直角三角形,选项A不符合题意;
B.∵∠A:∠B:∠C=3:3:5,
∴三角形中最大角∠C=×180°=90°,
∴满足条件的三角形为直角三角形,选项B不符合题意;
C.∵∠A=2∠B=3∠C,
∴∠A=,,∠C=,
∴选项C符合题意
D.∵一个外角等于和它相邻的一个内角,
∴该内角=×180°=90°,
∴满足条件的三角形为直角三角形,选项D不符合题意.
故选:C.
7.解:如图,
∵AC⊥AB,
∴∠3+∠1=90°,
∴∠8=90°﹣∠1=90°﹣35°=55°,
∵直线m∥n,
∴∠3=∠8=55°,
故选:C.
8.解:设∠A=∠3=x°,
则∠1=∠A+∠8=2x°,
∵∠ABC=∠C=∠1,
∴∠ABC=∠C=∠5=2x°,
∵∠A+∠ABC+∠C=180°,
∴x+2x+7x=180,
∴x=36,
∴∠A=36°,
故选:B.
9.解:∵图中是一副直角三角板,
∴∠A=30°,∠DCE=45°,
∴∠ACD=135°,
∴α=30°+135°=165°.
故选:A.
10.解:∵∠B+∠D+∠DAB+∠BCD=360°,∠B+∠ADC=140°,
∴∠DAB+∠BCD=360°﹣140°=220°,
∵∠α+∠β+∠DAB+∠BCD=360°,
∴∠α+∠β=360°﹣220°=140°,
故选:A.
二、填空题
11.解:结合图形,为了防止电线杆倾倒,两条拉线与地面就构成了三角形.
故答案为:三角形的稳定性.
12.解:①当20cm为底边时,第三边长为9cm,故不能构成三角形;
②当9cm为底边时,第三边长为20cm,故能构成三角形;
故答案为:20cm.
13.解:设∠A=2x°,则∠B=3x°,
∵∠A+∠B+∠C=180°,
即:2x°+3x°+4x°=180°,
解得:x=20
∴∠A=40°,则∠B=60°,
故答案为:40°、80°
14.解:∵在△ABC中,AD⊥BC于D,∠B=80°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣80°﹣46°=54°,
∴∠BAE=∠CAE==27°,
∵∠B=80°,AD⊥BC,
∴∠ADB=90°,
∴∠BAD=10°,
∴∠DAE=∠BAE﹣∠BAD=27°﹣10°=17°,
故答案为:17°.
15.解:∵m∥n,∠1=40°,
∴∠3=∠5=40°.
∵∠ACB=90°,
∴∠4=∠ACB﹣∠3=90°﹣40°=50°,
∴∠5=180°﹣∠4=180°﹣50°=130°.
故答案为:130.
16.解:∵∠BAD=28°,将△ABD沿AD折叠得到△AED,
∴∠BAD=∠FAD=28°,
∵∠B=48°,
∴∠ADF=∠B+∠BAD=48°+28°=76°,
∴∠AFC=∠FAD+∠ADF=28°+76°=104°,
故答案为:104.
17.解:∵∠1+∠2=120°,∠4+∠2+∠A=180°,
∴∠A=180°﹣(∠1+∠2)=60°,
∵五边形ABCDE的内角和为:(5﹣2)×180°=540°,
∴∠B+∠C+∠D+∠E=540°﹣∠A=540°﹣60°=480°,
故答案为:480°.
三、解答题
18.解:∠B=180°﹣∠BED﹣∠D
=180°﹣90°﹣50°
=40°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣33°﹣40°=107°.
19.解:设一边是2xcm,另一边为xcm,
根据题意,分情况讨论:
①以xcm为底边,
则2x+2x+x=15,
解得x=3,
∴2×4=6(cm),
∴三边长为6cm,5cm;
②以xcm为腰长,
根据三角形的三边关系,不能构成三角形,
综上所述,三边长为6cm,3cm.
20.解:设∠1=∠2=x,则∠4=∠4=2x.
因为∠BAC=63°,
所以∠5+∠4=117°,即x+2x=117°,
所以x=39°;
所以∠8=∠4=78°,
∠DAC=180°﹣∠3﹣∠7=24°.
21.解:五边形AOEFG的外角和为360°,
∵∠1,∠2,∠7的外角的角度和为220°,
∴∠AOE的外角为360°﹣220°=140°,
∵∠AOE=180°﹣140°=40°.
∴∠BOD=40°.
22.解:(1)∵AD⊥BC于D,
∴∠ADB=∠ADC=90°,
∵∠ABC=40°,∠C=60°,
∴∠BAD=50°,∠CAD=30°,
∴∠BAC=50°+30°=80°,
∵AE是∠BAC的平分线,
∴∠BAE=40°,
∴∠DAE=50°﹣40°=10°.
(2)AD是△ABE、△ABD、△AED、△ADC的高.
23.解:(1)∵∠ECF=∠ECB+∠BCF,
∴∠ECF+∠DAC+∠ECA
=(∠ECB+∠BCF)+∠DAC+∠ECA (∠BCF=∠BAD)
=(∠ECB+∠ECA)+(∠DAC+∠BAD)
=∠BCA+∠BAC
=45°+45°
=90°
即∠ECF+DAC+∠ECA=90°;
(2)ED和FC平行,理由如下:
∵∠EAD=∠AED=45°,
∴∠EDA=90°,
∴在C,E,D,A四点组成的凹四边形里,
∠ECA+∠CED+∠CAD=∠EDA=90°
又∵(1)的结论是∠ECF+DAC+∠ECA=90°,
∴∠CED=∠ECF,
∴DE∥CF(内错角相等,两直线平行).
24.解:(1)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠FBC+(180°﹣2∠DCF)=180°﹣8(∠DCF﹣∠FBC)=180°﹣2∠F,
∴360°﹣(α+β)=180°﹣2∠F,
7∠F=α+β﹣180°,
∴∠F=(α+β)﹣90°;
(2)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=8∠GBC+(180°﹣2∠HCE)=180°+2(∠GBC﹣∠HCE)=180°+2∠F,
∴360°﹣(α+β)=180°+2∠F,
∠F=90°﹣(α+β);
(3)当α+β=180°时,不存在∠F,
∵α+β=180°,
∴AB∥CD,
∴∠ABC的角平分线及外角∠DCE的平分线平行,
∴∠F不存在,
∴当α+β=180°时,不存在∠F.
