第12章 全等三角形 单元测试(含答案)2023-2024学年人教版八年级上册数学
文档属性
| 名称 | 第12章 全等三角形 单元测试(含答案)2023-2024学年人教版八年级上册数学 |
|
|
| 格式 | docx | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 00:00:00 | ||
图片预览



文档简介
《第12章 全等三角形》单元测试卷
班级 姓名
一.选择题(每小题3分,共36分)
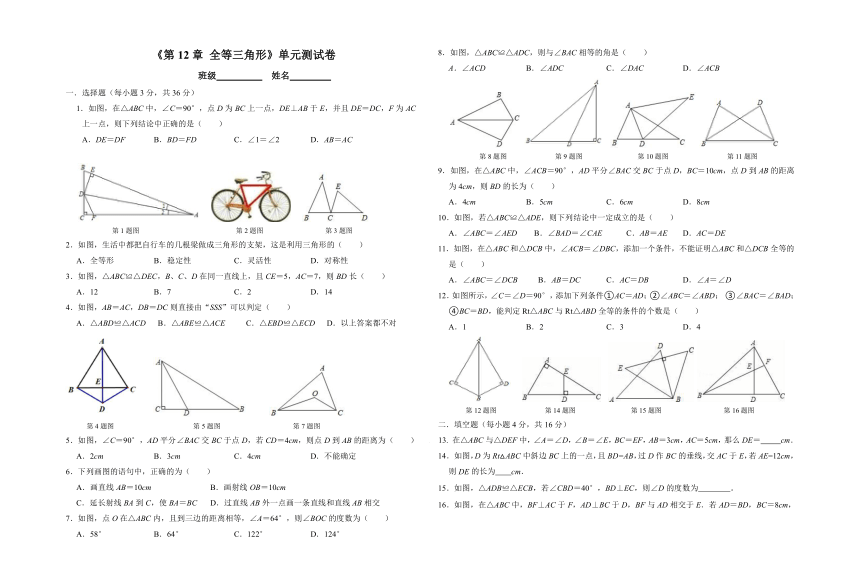
如图,在△ABC中,∠C=90°,点D为BC上一点,DE⊥AB于E,并且DE=DC,F为AC
上一点,则下列结论中正确的是( )
A.DE=DF B.BD=FD C.∠1=∠2 D.AB=AC
第1题图 第2题图 第3题图
2.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
3.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
4.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE C.△EBD≌△ECD D.以上答案都不对
第4题图 第5题图 第7题图
5.如图,∠C=90°,AD平分∠BAC交BC于点D,若CD=4cm,则点D到AB的距离为( )
A.2cm B.3cm C.4cm D.不能确定
6.下列画图的语句中,正确的为( )
A.画直线AB=10cm B.画射线OB=10cm
C.延长射线BA到C,使BA=BC D.过直线AB外一点画一条直线和直线AB相交
7.如图,点O在△ABC内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( )
A.58° B.64° C.122° D.124°
8.如图,△ABC≌△ADC,则与∠BAC相等的角是( )
∠ACD B.∠ADC C.∠DAC D.∠ACB
第8题图 第9题图 第10题图 第11题图
9.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=10cm,点D到AB的距离为4cm,则BD的长为( )
A.4cm B.5cm C.6cm D.8cm
10.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED B.∠BAD=∠CAE C.AB=AE D.AC=DE
11.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
12.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
第12题图 第14题图 第15题图 第16题图
填空题(每小题4分,共16分)
1 13. 在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE= cm.
如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 cm.
如图,△ADB≌△ECB,若∠CBD=40°,BD⊥EC,则∠D的度数为 .
如图,在△ABC中,BF⊥AC于F,AD⊥BC于D,BF与AD相交于E.若AD=BD,BC=8cm,
DC=3cm,则AE= cm.
解答题(共68分)
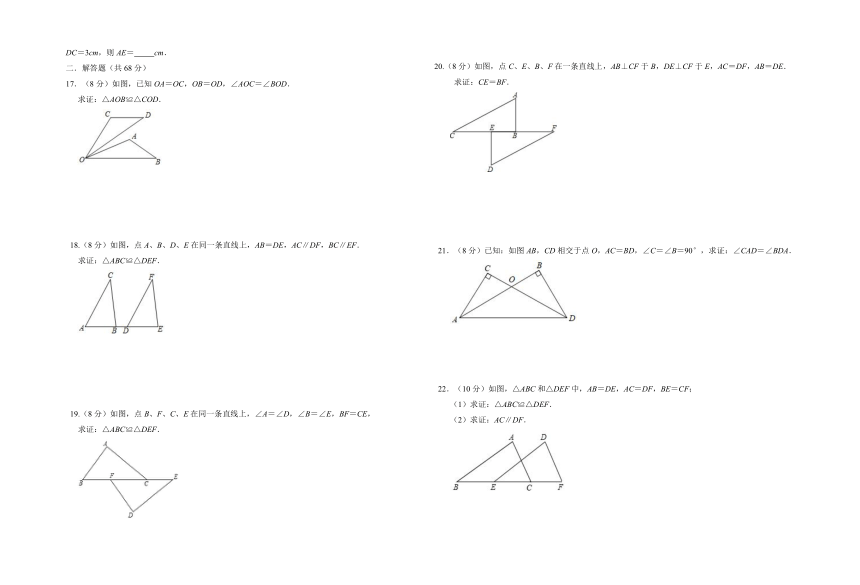
17.(8分)如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
18.(8分)如图,点A、B、D、E在同一条直线上,AB=DE,AC∥DF,BC∥EF.
求证:△ABC≌△DEF.
19.(8分)如图,点B、F、C、E在同一条直线上,∠A=∠D,∠B=∠E,BF=CE,
求证:△ABC≌△DEF.
20.(8分)如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.
求证:CE=BF.
21.(8分)已知:如图AB,CD相交于点O,AC=BD,∠C=∠B=90°,求证:∠CAD=∠BDA.
22.(10分)如图,△ABC和△DEF中,AB=DE,AC=DF,BE=CF;
(1)求证:△ABC≌△DEF.
(2)求证:AC∥DF.
23.(10分)公路上,A,B两站相距25千米,C、D为两所学校,DA⊥AB于点A,CB⊥AB于点B,如图,已知DA=15千米,现在要在公路AB上建一报亭H,使得C、D两所学校到H的距离相等,且∠DHC=90°,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?
如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.
若S△ABC=9,DE=2,AB=5,求AC的长.
25.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
26.(12分)已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
(1)若AM是△EAD中线,求证:AN⊥BC;
(2)若AN⊥BC,求证:EM=DM.
参考答案
1.解:(1)在直角三角形DCF中,利用斜边长度大于直角边长度,可以得到DF>DC,又DC=DE,所以DF>DE,
故A选项错误;
(2)△BDE与△DCF,只满足∠DEB=∠DCF=90°,DC=DE的条件,不能判定两个三角形全等,故不能得到BD=FD,
另一方面,假设BD=FD,
在Rt△DBE与△DFC中,
,
∴Rt△DBE≌Rt△DFC(HL),
∴∠B=∠DFC,
而图中∠B大小是固定的,∠DFC的大小随着F的变化而变化,故上述假设是不成立的,
故B选项错误;
(3)∵DC⊥AC,DE⊥AB,DC=DE,
利用角平分线的判定,
DC是∠BAC的平分线,
∴∠1=∠2,
故C选项正确;
(4)在直角三角形ABC中,利用斜边长度大于直角边长度,可以得到AB>AC,
故D选项错误,
故选:C.
2.解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故选:B.
3.解:∵△ABC≌△DEC,
∴AC=DC,CB=CE,
∵CE=5,AC=7,
∴CB=5,DC=7,
∴BD=DC+CB=7+5=12.
故选:A.
4.解:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS).
故选:A.
5.解:如图,过D点作DE⊥AB于点E,则DE的长即为所求,
∵∠C=90°,AD平分∠BAC交BC于点D,
∴CD=DE,
∵CD=4cm,
∴DE=4cm,即点D到AB的距离为4cm.
故选:C.
6.解:A、错误.直线没有长度;
B、错误.射线没有长度;
C、错误.射线有无限延伸性,不需要延长;
D、正确.
故选:D.
7.解:∵点O在△ABC内,且到三边的距离相等,
即O点到BA和BC的距离相等,O点到CA和CB的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠BOC=180°﹣∠OBC﹣∠OCB,
∴∠BOC=180°﹣(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣(180°﹣∠A)
=90°+∠A
=90°+×64°
=122°.
故选:C.
8.解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
故选:C.
9.解:过点D作DE⊥AB于E,
∵AD平分∠BAC,∠ACB=90°,DE⊥AB,
∴DC=DE=4cm,
∴BD=BC﹣DC=10﹣4=6(cm),
故选:C.
10.解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
11.解:在△ABC和△DCB中,
∵∠ACB=∠DBC,BC=BC,
A:当∠ABC=∠DCB时,△ABC≌△DCB(ASA),
故A能证明;
B:当AB=DC时,不能证明两三角形全等,
故B不能证明;
C:当AC=DB时,△ABC≌△DCB(SAS),
故C能证明;
D:当∠A=∠D时,△ABC≌△DCB(AAS),
故D能证明;
故选:B.
12.解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当∠ABC=∠ABD时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
③当∠BAC=∠BAD时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
④当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
故选:D.
13.解:如图:
在△ABC与△DEF中,
,
∴△ABC≌△DEF中(AAS),
∴AB=DE,
∵AB=3cm,
∴DE=3cm,
故答案为:3.
12
50°
2
17.证明:∵∠AOC=∠BOD,
∴∠AOC﹣∠AOD=∠BOD﹣∠AOD,
即∠COD=∠AOB,
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS).
18.证明:∵AC∥DF,
∴∠CAB=∠FDE(两直线平行,同位角相等),
又∵BC∥EF,
∴∠CBA=∠FED(两直线平行,同位角相等),
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
19.证明:∵BF=CE,
∴BF+FC=CE+FC即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
20.证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
∴BC=EF.
∴BC﹣BE=EF﹣BE.
即:CE=BF.
21.证明:∵∠C=∠B=90°
在△ACD与△DBA中,
.
∴△ACD≌△DBA(HL).
∴∠CAD=∠BDA.
22.解:(1)∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)由(1)知:△ABC≌△DEF,
∴∠DFE=∠ACB,
∴AC∥DF
23.解:∵∠DHC=90°,
∴∠AHD+∠CHB=90°,
∵DA⊥AB,
∴∠D+∠AHD=90°,
∴∠D=∠CHB,
在△ADH和△BHC中,,
∴△ADH≌△BHC(AAS),
∴AD=BH=15千米,AH=BC,
∵A,B两站相距25千米,
∴AB=25千米,
∴AH=AB﹣BH=25﹣15=10千米,
∴学校C到公路的距离是10千米.
答:H应建在距离A站10千米处,学校C到公路的距离是10千米.
24.解:∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=5,
∴9=×5×2+×AC×2,
∴AC=4.
25.证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在△DCF和△DEB中,,
∴△DCF≌△DEB,(SAS),
∴BD=DF.
26.证明:(1)如图,延长AM至F,使MF=AM,
∵AM是△EAD中线,
∴EM=DM,
在△EMF和△DMA中,
,
∴△EMF≌△DMA(SAS),
∴∠DAM=∠F,EF=AD,
∵AD=AC,
∴EF=AC,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(SAS),
∴∠EAF=∠B,
∵AE⊥AB,
∴∠EAF+∠BAN=90°,
∴∠B+∠BAN=90°,
在△ABN中,∠ANB=180°﹣(∠B+∠BAN)=180°﹣90°=90°,
∴AN⊥BC;
(2)如图,过点E作EF∥AD交AM的延长线于F,
则∠F=∠DAM,
∵DA⊥AC,
∴∠DAM+∠CAN=90°,
∵AN⊥BC,
∴∠CAN+∠C=90°,
∴∠F=∠DAM=∠C,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(AAS),
∴EF=AC,
∵AD=AC,
∴EF=AD,
在△EFM和△DAM中,
,
∴△EFM≌△DAM(AAS),
∴EM=DM.
班级 姓名
一.选择题(每小题3分,共36分)
如图,在△ABC中,∠C=90°,点D为BC上一点,DE⊥AB于E,并且DE=DC,F为AC
上一点,则下列结论中正确的是( )
A.DE=DF B.BD=FD C.∠1=∠2 D.AB=AC
第1题图 第2题图 第3题图
2.如图,生活中都把自行车的几根梁做成三角形的支架,这是利用三角形的( )
A.全等形 B.稳定性 C.灵活性 D.对称性
3.如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A.12 B.7 C.2 D.14
4.如图,AB=AC,DB=DC则直接由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE C.△EBD≌△ECD D.以上答案都不对
第4题图 第5题图 第7题图
5.如图,∠C=90°,AD平分∠BAC交BC于点D,若CD=4cm,则点D到AB的距离为( )
A.2cm B.3cm C.4cm D.不能确定
6.下列画图的语句中,正确的为( )
A.画直线AB=10cm B.画射线OB=10cm
C.延长射线BA到C,使BA=BC D.过直线AB外一点画一条直线和直线AB相交
7.如图,点O在△ABC内,且到三边的距离相等,∠A=64°,则∠BOC的度数为( )
A.58° B.64° C.122° D.124°
8.如图,△ABC≌△ADC,则与∠BAC相等的角是( )
∠ACD B.∠ADC C.∠DAC D.∠ACB
第8题图 第9题图 第10题图 第11题图
9.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=10cm,点D到AB的距离为4cm,则BD的长为( )
A.4cm B.5cm C.6cm D.8cm
10.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED B.∠BAD=∠CAE C.AB=AE D.AC=DE
11.如图,在△ABC和△DCB中,∠ACB=∠DBC,添加一个条件,不能证明△ABC和△DCB全等的是( )
A.∠ABC=∠DCB B.AB=DC C.AC=DB D.∠A=∠D
12.如图所示,∠C=∠D=90°,添加下列条件①AC=AD;②∠ABC=∠ABD; ③∠BAC=∠BAD; ④BC=BD,能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.1 B.2 C.3 D.4
第12题图 第14题图 第15题图 第16题图
填空题(每小题4分,共16分)
1 13. 在△ABC与△DEF中,∠A=∠D,∠B=∠E,BC=EF,AB=3cm,AC=5cm,那么DE= cm.
如图,D为Rt△ABC中斜边BC上的一点,且BD=AB,过D作BC的垂线,交AC于E,若AE=12cm,则DE的长为 cm.
如图,△ADB≌△ECB,若∠CBD=40°,BD⊥EC,则∠D的度数为 .
如图,在△ABC中,BF⊥AC于F,AD⊥BC于D,BF与AD相交于E.若AD=BD,BC=8cm,
DC=3cm,则AE= cm.
解答题(共68分)
17.(8分)如图,已知OA=OC,OB=OD,∠AOC=∠BOD.
求证:△AOB≌△COD.
18.(8分)如图,点A、B、D、E在同一条直线上,AB=DE,AC∥DF,BC∥EF.
求证:△ABC≌△DEF.
19.(8分)如图,点B、F、C、E在同一条直线上,∠A=∠D,∠B=∠E,BF=CE,
求证:△ABC≌△DEF.
20.(8分)如图,点C、E、B、F在一条直线上,AB⊥CF于B,DE⊥CF于E,AC=DF,AB=DE.
求证:CE=BF.
21.(8分)已知:如图AB,CD相交于点O,AC=BD,∠C=∠B=90°,求证:∠CAD=∠BDA.
22.(10分)如图,△ABC和△DEF中,AB=DE,AC=DF,BE=CF;
(1)求证:△ABC≌△DEF.
(2)求证:AC∥DF.
23.(10分)公路上,A,B两站相距25千米,C、D为两所学校,DA⊥AB于点A,CB⊥AB于点B,如图,已知DA=15千米,现在要在公路AB上建一报亭H,使得C、D两所学校到H的距离相等,且∠DHC=90°,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?
如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F.
若S△ABC=9,DE=2,AB=5,求AC的长.
25.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
26.(12分)已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
(1)若AM是△EAD中线,求证:AN⊥BC;
(2)若AN⊥BC,求证:EM=DM.
参考答案
1.解:(1)在直角三角形DCF中,利用斜边长度大于直角边长度,可以得到DF>DC,又DC=DE,所以DF>DE,
故A选项错误;
(2)△BDE与△DCF,只满足∠DEB=∠DCF=90°,DC=DE的条件,不能判定两个三角形全等,故不能得到BD=FD,
另一方面,假设BD=FD,
在Rt△DBE与△DFC中,
,
∴Rt△DBE≌Rt△DFC(HL),
∴∠B=∠DFC,
而图中∠B大小是固定的,∠DFC的大小随着F的变化而变化,故上述假设是不成立的,
故B选项错误;
(3)∵DC⊥AC,DE⊥AB,DC=DE,
利用角平分线的判定,
DC是∠BAC的平分线,
∴∠1=∠2,
故C选项正确;
(4)在直角三角形ABC中,利用斜边长度大于直角边长度,可以得到AB>AC,
故D选项错误,
故选:C.
2.解:生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
故选:B.
3.解:∵△ABC≌△DEC,
∴AC=DC,CB=CE,
∵CE=5,AC=7,
∴CB=5,DC=7,
∴BD=DC+CB=7+5=12.
故选:A.
4.解:在△ABD与△ACD中,
,
∴△ABD≌△ACD(SSS).
故选:A.
5.解:如图,过D点作DE⊥AB于点E,则DE的长即为所求,
∵∠C=90°,AD平分∠BAC交BC于点D,
∴CD=DE,
∵CD=4cm,
∴DE=4cm,即点D到AB的距离为4cm.
故选:C.
6.解:A、错误.直线没有长度;
B、错误.射线没有长度;
C、错误.射线有无限延伸性,不需要延长;
D、正确.
故选:D.
7.解:∵点O在△ABC内,且到三边的距离相等,
即O点到BA和BC的距离相等,O点到CA和CB的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠BOC=180°﹣∠OBC﹣∠OCB,
∴∠BOC=180°﹣(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣(180°﹣∠A)
=90°+∠A
=90°+×64°
=122°.
故选:C.
8.解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
故选:C.
9.解:过点D作DE⊥AB于E,
∵AD平分∠BAC,∠ACB=90°,DE⊥AB,
∴DC=DE=4cm,
∴BD=BC﹣DC=10﹣4=6(cm),
故选:C.
10.解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
11.解:在△ABC和△DCB中,
∵∠ACB=∠DBC,BC=BC,
A:当∠ABC=∠DCB时,△ABC≌△DCB(ASA),
故A能证明;
B:当AB=DC时,不能证明两三角形全等,
故B不能证明;
C:当AC=DB时,△ABC≌△DCB(SAS),
故C能证明;
D:当∠A=∠D时,△ABC≌△DCB(AAS),
故D能证明;
故选:B.
12.解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当∠ABC=∠ABD时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
③当∠BAC=∠BAD时,由∠C=∠D=90°,∠BAC=∠BAD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
④当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
故选:D.
13.解:如图:
在△ABC与△DEF中,
,
∴△ABC≌△DEF中(AAS),
∴AB=DE,
∵AB=3cm,
∴DE=3cm,
故答案为:3.
12
50°
2
17.证明:∵∠AOC=∠BOD,
∴∠AOC﹣∠AOD=∠BOD﹣∠AOD,
即∠COD=∠AOB,
在△AOB和△COD中,
,
∴△AOB≌△COD(SAS).
18.证明:∵AC∥DF,
∴∠CAB=∠FDE(两直线平行,同位角相等),
又∵BC∥EF,
∴∠CBA=∠FED(两直线平行,同位角相等),
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA).
19.证明:∵BF=CE,
∴BF+FC=CE+FC即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(AAS).
20.证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL).
∴BC=EF.
∴BC﹣BE=EF﹣BE.
即:CE=BF.
21.证明:∵∠C=∠B=90°
在△ACD与△DBA中,
.
∴△ACD≌△DBA(HL).
∴∠CAD=∠BDA.
22.解:(1)∵BE=CF,
∴BE+CE=CF+CE,即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)由(1)知:△ABC≌△DEF,
∴∠DFE=∠ACB,
∴AC∥DF
23.解:∵∠DHC=90°,
∴∠AHD+∠CHB=90°,
∵DA⊥AB,
∴∠D+∠AHD=90°,
∴∠D=∠CHB,
在△ADH和△BHC中,,
∴△ADH≌△BHC(AAS),
∴AD=BH=15千米,AH=BC,
∵A,B两站相距25千米,
∴AB=25千米,
∴AH=AB﹣BH=25﹣15=10千米,
∴学校C到公路的距离是10千米.
答:H应建在距离A站10千米处,学校C到公路的距离是10千米.
24.解:∵AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,
∴DF=DE=2.
又∵S△ABC=S△ABD+S△ACD,AB=5,
∴9=×5×2+×AC×2,
∴AC=4.
25.证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在△DCF和△DEB中,,
∴△DCF≌△DEB,(SAS),
∴BD=DF.
26.证明:(1)如图,延长AM至F,使MF=AM,
∵AM是△EAD中线,
∴EM=DM,
在△EMF和△DMA中,
,
∴△EMF≌△DMA(SAS),
∴∠DAM=∠F,EF=AD,
∵AD=AC,
∴EF=AC,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(SAS),
∴∠EAF=∠B,
∵AE⊥AB,
∴∠EAF+∠BAN=90°,
∴∠B+∠BAN=90°,
在△ABN中,∠ANB=180°﹣(∠B+∠BAN)=180°﹣90°=90°,
∴AN⊥BC;
(2)如图,过点E作EF∥AD交AM的延长线于F,
则∠F=∠DAM,
∵DA⊥AC,
∴∠DAM+∠CAN=90°,
∵AN⊥BC,
∴∠CAN+∠C=90°,
∴∠F=∠DAM=∠C,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(AAS),
∴EF=AC,
∵AD=AC,
∴EF=AD,
在△EFM和△DAM中,
,
∴△EFM≌△DAM(AAS),
∴EM=DM.
