第23章 旋转 单元综合训练(无答案)2022-2023学年人教版数学九年级上学期
文档属性
| 名称 | 第23章 旋转 单元综合训练(无答案)2022-2023学年人教版数学九年级上学期 |

|
|
| 格式 | docx | ||
| 文件大小 | 572.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 00:00:00 | ||
图片预览

文档简介
第23章 旋转 单元综合训练
一、单选题
1.下面四个图案中,是中心对称图形的是( )
A. B. C. D.
2.已知点与点关于原点对称,则的值为( )
A.2 B.1 C. D.
3.如图,,将绕点按逆时针方向旋转后得到,若,则的度数是( )
A. B. C. D.
4.如图,菱形的对角线相交于坐标原点,点A的坐标为,点B的坐标为,那么点C的坐标为( )
A. B. C. D.
5.利用图形的旋转可以设计出许多美丽的图案.图2中的图案是由图1中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为,则旋转角的值不可能为( )
A. B. C. D.
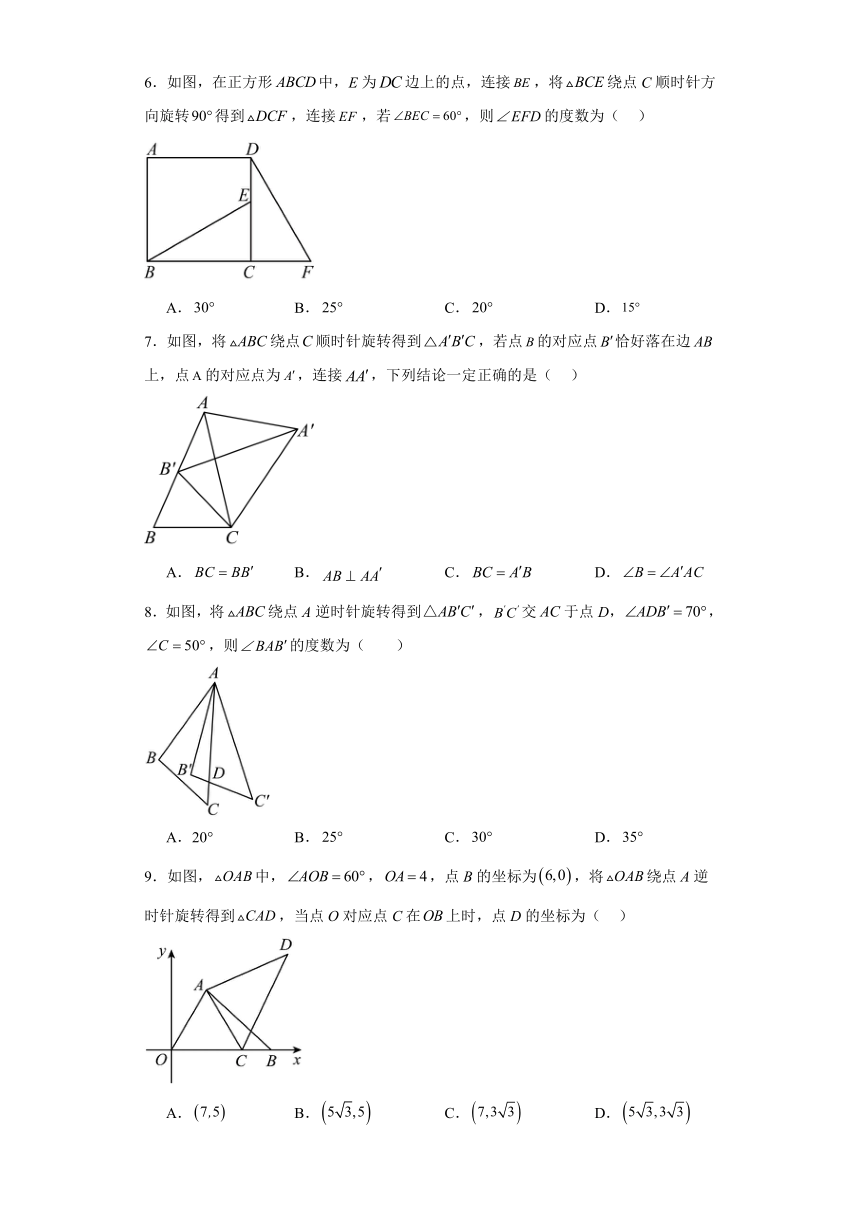
6.如图,在正方形中,E为边上的点,连接,将绕点C顺时针方向旋转得到,连接,若,则的度数为( )
A. B. C. D.
7.如图,将绕点顺时针旋转得到,若点的对应点恰好落在边上,点的对应点为,连接,下列结论一定正确的是( )
A. B. C. D.
8.如图,将绕点A逆时针旋转得到,交于点D,,,则的度数为( )
A.20° B. C. D.
9.如图,中,,,点B的坐标为,将绕点A逆时针旋转得到,当点O对应点C在上时,点D的坐标为( )
A. B. C. D.
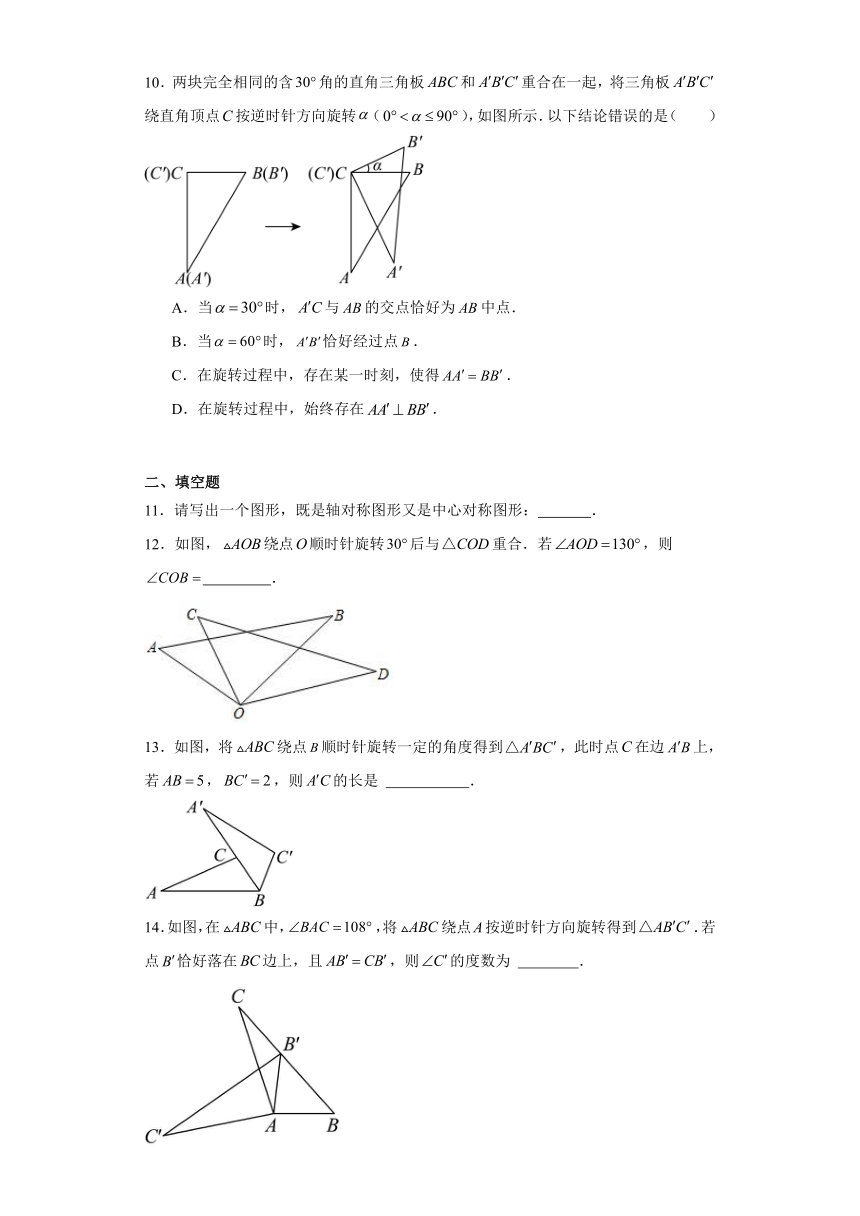
10.两块完全相同的含角的直角三角板和重合在一起,将三角板绕直角顶点按逆时针方向旋转(),如图所示.以下结论错误的是( )
A.当时,与的交点恰好为中点.
B.当时,恰好经过点.
C.在旋转过程中,存在某一时刻,使得.
D.在旋转过程中,始终存在.
二、填空题
11.请写出一个图形,既是轴对称图形又是中心对称图形: .
12.如图,绕点顺时针旋转后与重合.若,则 .
13.如图,将绕点顺时针旋转一定的角度得到,此时点在边上,若,,则的长是 .
14.如图,在中,,将绕点A按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为 .
15.如图,已知与关于点成中心对称,则的长是 .
16.如图,在中,,将绕点顺时针方向旋转得到,交于点F,连接,则当是等腰三角形时,旋转角 .
三、解答题
17.如图, 在边长为1的小正方形组成的方格纸上,分别将△ABC向左平移3个单位和绕着点A顺时针旋转90°
(1)画出平移后的△
(2)画出旋转之后的△
18.如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC以x轴为对称轴,画出对称后的△A1B1C1;
(2)将△ABC绕点C逆时针旋转90°,画出旋转后的△,并请你直接写出的长度 .
19.如图,为等边内一点,将线段绕点逆时针旋转,得到线段,连接,.
(1)求证:;
(2)连接,若,求的度数.
20.如图,点是正方形内部的一点,,将绕点A按逆时针方向旋转得到,,的延长线相交于点E.若正方形的边长为10,.
(1)求证:四边形是正方形;
(2)求的长.
21.如图,将绕直角顶点B逆时针旋转得到,的延长线恰好经过的中点,连接,.
(1)求证:.
(2)若,求的长.
22.已知:如图,在中,,以为边向形外作等边三角形, 把绕着点D按顺时针方向旋转后得到,若,
(1)求的度数;
(2)的长.
23.已知.
(1)如图1,CB平分,求证;;
(2)如图2,将(1)中的绕点C逆时针旋转(旋转角小于),BC,DE的延长线相交于点F,用等式表示与之间的数量关系,并证明;
(3)如图3,将(1)中的绕点C顺时针旋转(旋转角小于),若,求的度数.
24.如图,是正方形内一点,将绕点顺时针方向旋转得到.
(1)观察猜想:如图1,线段与的数量关系是 ,位置关系是 .
(2)探究实践:如图2,连接,若,,,求.
(3)拓展延伸:如图3,把绕点在平面内自由旋转,若,,当,,三点在一条直线上时,请直接写出 .
一、单选题
1.下面四个图案中,是中心对称图形的是( )
A. B. C. D.
2.已知点与点关于原点对称,则的值为( )
A.2 B.1 C. D.
3.如图,,将绕点按逆时针方向旋转后得到,若,则的度数是( )
A. B. C. D.
4.如图,菱形的对角线相交于坐标原点,点A的坐标为,点B的坐标为,那么点C的坐标为( )
A. B. C. D.
5.利用图形的旋转可以设计出许多美丽的图案.图2中的图案是由图1中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为,则旋转角的值不可能为( )
A. B. C. D.
6.如图,在正方形中,E为边上的点,连接,将绕点C顺时针方向旋转得到,连接,若,则的度数为( )
A. B. C. D.
7.如图,将绕点顺时针旋转得到,若点的对应点恰好落在边上,点的对应点为,连接,下列结论一定正确的是( )
A. B. C. D.
8.如图,将绕点A逆时针旋转得到,交于点D,,,则的度数为( )
A.20° B. C. D.
9.如图,中,,,点B的坐标为,将绕点A逆时针旋转得到,当点O对应点C在上时,点D的坐标为( )
A. B. C. D.
10.两块完全相同的含角的直角三角板和重合在一起,将三角板绕直角顶点按逆时针方向旋转(),如图所示.以下结论错误的是( )
A.当时,与的交点恰好为中点.
B.当时,恰好经过点.
C.在旋转过程中,存在某一时刻,使得.
D.在旋转过程中,始终存在.
二、填空题
11.请写出一个图形,既是轴对称图形又是中心对称图形: .
12.如图,绕点顺时针旋转后与重合.若,则 .
13.如图,将绕点顺时针旋转一定的角度得到,此时点在边上,若,,则的长是 .
14.如图,在中,,将绕点A按逆时针方向旋转得到.若点恰好落在边上,且,则的度数为 .
15.如图,已知与关于点成中心对称,则的长是 .
16.如图,在中,,将绕点顺时针方向旋转得到,交于点F,连接,则当是等腰三角形时,旋转角 .
三、解答题
17.如图, 在边长为1的小正方形组成的方格纸上,分别将△ABC向左平移3个单位和绕着点A顺时针旋转90°
(1)画出平移后的△
(2)画出旋转之后的△
18.如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)将△ABC以x轴为对称轴,画出对称后的△A1B1C1;
(2)将△ABC绕点C逆时针旋转90°,画出旋转后的△,并请你直接写出的长度 .
19.如图,为等边内一点,将线段绕点逆时针旋转,得到线段,连接,.
(1)求证:;
(2)连接,若,求的度数.
20.如图,点是正方形内部的一点,,将绕点A按逆时针方向旋转得到,,的延长线相交于点E.若正方形的边长为10,.
(1)求证:四边形是正方形;
(2)求的长.
21.如图,将绕直角顶点B逆时针旋转得到,的延长线恰好经过的中点,连接,.
(1)求证:.
(2)若,求的长.
22.已知:如图,在中,,以为边向形外作等边三角形, 把绕着点D按顺时针方向旋转后得到,若,
(1)求的度数;
(2)的长.
23.已知.
(1)如图1,CB平分,求证;;
(2)如图2,将(1)中的绕点C逆时针旋转(旋转角小于),BC,DE的延长线相交于点F,用等式表示与之间的数量关系,并证明;
(3)如图3,将(1)中的绕点C顺时针旋转(旋转角小于),若,求的度数.
24.如图,是正方形内一点,将绕点顺时针方向旋转得到.
(1)观察猜想:如图1,线段与的数量关系是 ,位置关系是 .
(2)探究实践:如图2,连接,若,,,求.
(3)拓展延伸:如图3,把绕点在平面内自由旋转,若,,当,,三点在一条直线上时,请直接写出 .
同课章节目录
