人教B版(2019)必修第二册 5.4统计与概率的应用 同步练习(含解析)
文档属性
| 名称 | 人教B版(2019)必修第二册 5.4统计与概率的应用 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 00:00:00 | ||
图片预览




文档简介
5.4统计与概率的应用同步练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.假设第一次感染新冠病毒并且康复后3个月内二次感染的概率大约是0.03,在半年内二次感染的概率是0.5.若某人第一次感染新冠病毒康复后,已经过去了三个月一直身体健康,在未来三个月内此人二次感染的概率是( )
A.0.45 B.0.48. C.0.49 D.0.47.
2.七巧板又称七巧图,智慧板,是一种古老的中国传统智力玩具.据清代陆以湉《冷庐杂识》说:“宋黄伯思宴几图,以方几七,长段相参,衍为二十五体,变为六十八名.明严澈蝶几图,则又变通其制,以勾股之形,作三角相错形,如蝶翅.其式三,其制六,其数十有三,其变化之式,凡一百有余.近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.”如图是一个用七巧板拼成的三角形(其中①②为两块全等的小型等腰直角三角形;③为一块中型等腰直角三角形;④⑤为两块全等的大型等腰直角三角形;⑥为一块正方形;⑦为一块平行四边形).现从该三角形中任取一点,则此点取自阴影部分的概率为( )
A. B. C. D.
3.已知某厂的产品合格率为0.7,现抽出10件产品检查,则下列说法正确的是( )
A.合格产品少于7件 B.合格产品多于7件
C.合格产品正好是7件 D.合格产品可能是7件
4.随着我国经济社会加快发展,人们思想观念不断更新,女性在企业管理中占据着越来越重要的地位,2021年12月21日,国家统计局发布了《中国妇女发展纲要(2011—2020年)》终期统计监测报告.下图为2010—2020年企业职工董事和职工监事中女性所占比重条形统计图,根据此图,判断下列说法错误的是( )
A.2010—2020年企业职工董事中女性所占比重的平均值为35.0个百分点
B.2020年企业职工董事中女性比重比2010年提高2.2个百分点
C.2020年企业职工监事中女性比重比2010年提高3.0个百分点
D.2011年企业职工监事中女性比重与董事中女性比重的差最大
5.已知与满足,若的中位数为6,则的中位数为( )
A.6 B.12 C.15 D.24
6.七巧板,又称七巧图、智慧板,是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,于明、清两代在民间广泛流传.某同学用边长为4 dm的正方形木板制作了一套七巧板,如图所示,包括5个等腰直角三角形,1个正方形和1个平行四边形.若该同学从5个三角形中任取出2个,则这2个三角形的面积之和不小于另外3个三角形面积之和的概率是( )
A. B. C. D.
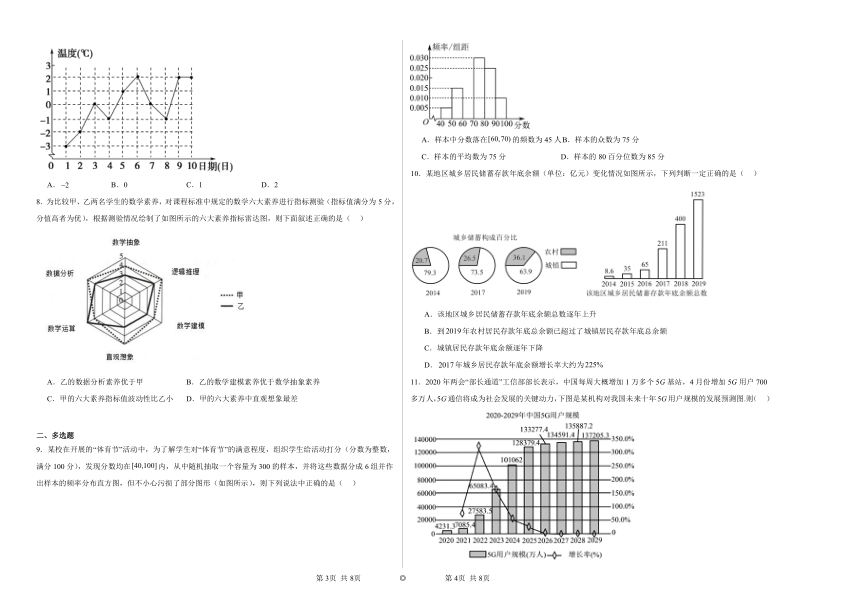
7.如图所示是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这10天最低气温的第80百分位数是( )
A. B.0 C.1 D.2
8.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
二、多选题
9.某校在开展的“体育节”活动中,为了解学生对“体育节”的满意程度,组织学生给活动打分(分数为整数,满分100分),发现分数均在内,从中随机抽取一个容量为300的样本,并将这些数据分成6组并作出样本的频率分布直方图,但不小心污损了部分图形(如图所示),则下列说法中正确的是( )
A.样本中分数落在的频数为45人 B.样本的众数为75分
C.样本的平均数为75分 D.样本的80百分位数为85分
10.某地区城乡居民储蓄存款年底余额(单位:亿元)变化情况如图所示,下列判断一定正确的是( )
A.该地区城乡居民储蓄存款年底余额总数逐年上升
B.到年农村居民存款年底总余额已超过了城镇居民存款年底总余额
C.城镇居民存款年底余额逐年下降
D.年城乡居民存款年底余额增长率大约为
11.2020年两会“部长通道”工信部部长表示,中国每周大概增加1万多个5G基站,4月份增加5G用户700多万人,5G通信将成为社会发展的关键动力,下图是某机构对我国未来十年5G用户规模的发展预测图.则( )
A.2022年我国5G用户规模年增长率最高
B.2022年我国5G用户规模年增长户数最多
C.从2020年到2026年,我国的5G用户规模增长两年后,其年增长率逐年下降
D.这十年我国的5G用户数规模,后5年的平均数与方差都分别大于前5年的平均数与方差
12.甲、乙两人下棋,和棋的概率为,乙获胜的概率为,则下列说法错误的是( )
A.甲获胜的概率是 B.甲不输的概率是
C.乙输的概率是 D.乙不输的概率是
三、填空题
13.《定理汇编》记载了诸多重要的几何定理,其中有一些定理是关于鞋匠刀形的,即由在同一直线上同侧的三个半圆所围成的图形,其被阿基米德称为鞋匠刀形.如图所示,三个半圆的圆心分别为,,,半径分别为,,(其中),在半圆О内随机取一点,此点取自图中鞋匠刀形(阴影部分)的概率为,则 .
14.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何 ”其意为:“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则乙应出(所得结果四舍五入,保留整数)钱数为 .
15.若样本数据是以频率分布直方图的形式给出,这时已不存在原始数据,因此要确定其p%分位数,只能估算,其p%分位数即为频率分布直方图中使左侧小矩形面积之和等于p%的分点值.
例如:若某校100名学生的数学测试成绩的频率分布直方图如图:则可估计其80%分位数为 .
16.对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为的数据不慎丢失,则依据此图可得:
(1)年龄组为对应小矩形的高度为 ;
(2)由频率分布直方图估计志愿者年龄的85%分位数为 岁(结果保留整数).
四、解答题
17.某山村海拔较高,交通极为不便,被称为“云端上的村庄”,系建档立卡贫困村.民政部门为此组建了精准扶贫队对该村进行定点帮扶,扶贫组在实地调研后,立足当地独特优势,大力发展乡村经济,带动全村父老乡亲脱贫奔小康.为了解贫困户的帮扶情况,该地民政部门从本村的贫困户中随机抽取100户对去年的年收入进行了一个抽样调查,得到如下表所示的频数表:
收入(千元)
频数 15 10 35 20 10 10
(1)估计本村的贫困户的年收入的众数、第75百分位数;
(2)用分层抽样的方法从这100户贫困户抽取20户贫困户进行帮扶,若再从抽样调查收入在和的贫困户中随机选取2户作为重点帮扶对象,求至少有一户来自收入在千元的概率;
18.某校为了解学生每日行走的步数,在全校3000名学生中随机抽取200名,给他们配发了计步手环,统计他们的日行步数,按步数分组,得到频率分布直方图如图所示,
(1)求的值,并求出这200名学生日行步数的样本众数、中位数、平均数;
(2)学校为了鼓励学生加强运动,决定对步数大于或等于13000步的学生加1分,计入期末三好学生评选的体育考核分,估计全校每天获得加分的人数.
19.中华人民共和国第十四届全国运动会、全国第十一届残运会暨第八届特奥会将于2021年在中国陕西举行.为宣传全运会、特奥会,让更多的人了解体育运动项目和体育精神,某大学举办了全运会、特奥会知识竞赛,并从中随机抽取了100名学生的成绩,绘制成如图所示的频率分布直方图.
(1)试根据频率分布直方图求出这100人中成绩低于60分的人数,并估计这100人的平均成绩(同一组数据用该组区间的中点值代替);
(2)求出随机抽取的100名学生成绩的第50百分位数(结果保留到小数点后一位);
(3)若采用分层抽样的方法从成绩在,,的学生中共抽取6人,把6人排成一列,求成绩在的学生站在一起的概率.
20.在某地区,某项职业的从业者共约8.5万人,其中约3.4万人患有某种职业病:为了解这种职业病与某项身体指标(检测值为不超过6的正整数)间的关系,依据是否患有职业病,使用分层抽样的方法随机抽取了100名从业者,记录他们该项身体指标的检测值,整理得到如下统计图:
(1)求样本中患病者的人数和图中a,b的值;
(2)试估计此地区该项身体指标检测值不低于5的从业者的人数;
(3)某研究机构提出,可以选取常数,若一名从业者该项身体指标检测值大于,则判定其患有这种职业病;若检测值小于,则判定其未患有这种职业病.从样本中随机选择一名从业者,按照这种方式判断其是否患病,求判断错误的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】理解题意,康复后半年内感染的概率为康复后三个月感染的概率和康复后前三个月健康而未来三个月感染的概率之和,建立方程式解出即可.
【详解】令康复后前三个月健康而未来三个月内二次感染的概率为,
则可得:,
解得;
故选:B.
2.B
【分析】数形结合,通过对图形的各点标记,以及各块几何图的性质,进行边长运算即可得出结论.
【详解】如图,
为等腰直角三角形, 连接,
由题可知, 分别为的中点,
设,则,, , ,
则,
阴影部分②的面积为,
阴影部分⑦的面积为
则从该三角形中任取一点,则此点取自阴影部分的概率为,
故选:B.
3.D
【分析】根据概率的定义和性质直接求解即可.
【详解】根据概率的性质可计算出合格产品可能是件,
故选:D.
4.A
【分析】本题考查学生筛选整合信息,处理信息的能力。此类题要求学生在对题目内容的理解与辨析,找出文章条形统计图中相对应的信息并进行计算,即可得到结论.
【详解】解:2010—2020年企业职工董事中女性所占比重的平均值为个百分点,选项A错误;
2020年企业职工董事中女性比重比2010年提高34.9-32.7=2.2个百分点,选项B正确;
2020年企业职工监事中女性比重比2010年提高38.2-35.2=3.0个百分点,选项C正确;
2011年企业职工监事中女性比重与董事中女性比重的差最大,为4个百分点,选项D正确.
故选:A.
5.C
【分析】由于中,与 成正比,记 为的中位数,则中对应的中位数为.; 从而求出的中位数.
【详解】解:记 为的中位数,为中对应的中位数
因为,,
所以为
故选C.
6.D
【分析】先逐个求解所有5个三角形的面积,再根据要求计算概率.
【详解】如图所示,,,,,的面积分别为,,.
将,,,,分别记为,,,,,从这5个三角形中任取出2个,则样本空间,共有10个样本点.
记事件表示“从5个三角形中任取出2个,这2个三角形的面积之和不小于另外3个三角形面积之和”,则事件包含的样本点为,,,共3个,所以.
故选:D.
7.D
【分析】利用百分位数的定义即可得解;
【详解】由折线图可知,这10天的最低气温按照从小到大的顺序排列为:,,,,0,0,1,2,2,2,
因为共有10个数据,所以是整数,
则这10天最低气温的第80百分位数是.
故选:D
8.C
【分析】根据所给的六大素养雷达图逐个分析即可.
【详解】A选项,甲的数据分析素养为分, 乙的数据分析素养为分, 乙的数据分析素养低于甲,选项错误;
B选项,乙的数学建模素养为分, 乙的数学抽象为素养分,选项错误;
C选项, 甲的六大素养指标值分别为,,,,,;乙的六大素养指标值分别为,,,,,,甲的六大素养指标值波动性比乙小,选项正确;
D选项,由C可知,甲的六大素养中,数学抽象,数学建模和数学运算最差,直观想象最最好,选项错误;
故选C.
【点睛】本题考查了命题真假的判断以及统计图雷达图的识别和应用,考查学生简单的推理,属于基础题.
9.AB
【分析】根据频率分布直方图得到各组概率,根据概率和为1得到分数落在的频率进而求解其频数,从而判断A;根据频率最高的区间得到众数,从而判断B;根据频率分布直方图的平均数与百分位数求法计算,从而判断C和D.
【详解】设分数落在的频率为,
由题意得,各组频率依次为,,,,,,
所以,解得.
对于A,样本中分数落在的频数为人,故A正确;
对于B,由题意知,样本中的频率最高,所以众数为75分,故B正确;
对于C,样本的平均数为分,故C错误;
对于D,分数小于80的频率为,分数小于90的频率为,所以样本的80百分位数位于,设为,
则,解得,故D错误.
故选:AB
10.AD
【解析】结合扇形图与条形图分析对比,对选项逐一分析判断.
【详解】由条形图可知,余额总数逐年上升,故A项正确;由城乡储蓄构成百分比可知,年农村居民存款年底总余额占,城镇居民存款年底总余额占,没有超过,故B项错误;城镇居民存款年底余额所占的比重逐年下降,但城镇居民存款年底余额年,年,年分别为(亿元),(亿元),(亿元),总体不是逐年下降的,故C项错误,年城乡居民存款年底余额增长率大约为,故D项正确.
故选:AD.
11.AC
【分析】由图表中所给数据进行分析判断即可.
【详解】由图表可得,年5G用户规模年增长率最高,故A正确;
年5G用户规模年增长户数最多为(万人),故B错;
由图表可知,从年开始,年与年5G用户规模年增长率增加,从年开始到年5G用户规模年增长率逐年递减,故C正确;
由于后五年5G用户数增长不大,数据较稳定,故方差小于前5年数据方差,所以D错.
故选:AC.
【点睛】本题考查统计图表的运用,考查学生读图获取信息的能力,较简单.
12.BCD
【分析】由对立事件、互斥事件、并事件的概率计算公式代入计算,对选项逐一判断.
【详解】“甲获胜”是“和棋或乙获胜”的对立事件,所以“甲获胜”的概率是,故A正确;设甲不输为事件A,则事件A是“甲获胜”和“和棋”这两个互斥事件的并事件,所以,故B错误;“乙输”的概率即“甲获胜”的概率,为,故C错误;设乙不输为事件B,则事件B是“乙获胜”和“和棋”这两个互斥事件的并事件,所以,故D错误;
故选:BCD
13./
【分析】通过计算三个半圆的面积,表示阴影部分的面积,利用几何概型的概率计算公式即可得出答案.
【详解】解:阴影部分面积为:
由图可知:,所以
则,
因为在半圆О内随机取一点,此点取自图中鞋匠刀形(阴影部分)的概率为,
所以,
,即,则
解得:,因为,
所以.
故答案为:.
14.32
【分析】根据甲乙丙所带钱数,可以计算出所交关税在全部钱中的占比,根据该比例,可算出乙应出的钱数.
【详解】由题可知:甲乙丙所带钱数的总和为:560+350+180=1090,
故关税缴纳的比例为:,
所以:乙应该出钱:.
故答案为:32.
【点睛】本题考查分层抽样在实际问题中的应用,需要注意每层的抽样比例与整体的抽样比例相等.
15.133.3.
【解析】根据分位数的定义计算可得.
【详解】解析:分数在130以下的学生所占比例为.
在140以下的学生所占比例为.
因此,80%分位数一定位于内,由.
可以估计80%分位数为133.3.
答案:133.3.
【点睛】本题考查分位数的概念,属于基础题.
16. 0.04/ 39
【分析】(1)根据频率分布直方图的特征及图中数据,列等式计算即可;
(2)根据分位数的定义及题中数据计算可得出结果.
【详解】(1)设所对应小矩形的高度为,根据题意,
,计算得, ;
(2)根据分位数的定义,设志愿者年龄的85%分位数为x,则
解得.
故答案为:0.04;39.
17.(1)11,13.5;
(2).
【分析】(1)根据频数表求众数及百位数即可;
(2)根据分层抽样可得在和范围抽取的贫困户数分别为3户和2户,再利用古典概型计算概率即可.
【详解】(1)众数为;
由于前三组的频率之和为,
前四组的频率之和为
∴第75百分位数在第4组中,
设第75百分位数为,则有:,解得:,
即第75百分位数为13.5;
(2)由频数表及分层抽样可知在收入范围内抽取的户数为,在收入范围内抽取的户数,
记年收入在的3名贫困户分别为A,,,年收入在的2名贫困户分别为,,
则从中随机抽取2户的所有可能结果为:,,,,,,,,,共10种,
其中抽到至少有一名在的贫困户的可能结果:,,,,,,有7种,
故年收入在的贫困户至少有1人被抽到的概率:.
18.(1)的值为0.1,众数为千步,中位数为千步,平均数为9.44千步
(2)360
【分析】(1)结合频率分布直方图,根据概率之和为1求出的值,进而结合图求解样本众数、中位数、平均数;
(2)根据已知条件求出步数大于或等于13000步的学生的频率,从而估计全校每天获得加分的人数即可.
【详解】(1)根据频率分布直方图可知,各组频率依次为,,,,,,,,
所以,
解得;
因为组频率最高,所以样本众数为千步;
步数小于8的频率为,步数小于10的频率为,所以中位数在之间,记为x,
则,解得,
所以中位数为千步;
平均数为,
所以平均数为9.44千步.
(2)由表可知,大于或等于13000步的学生频率为,
将频率看作概率,
则全校每天获得加分的人数约为(人),
所以估计全校每天获得加分的人数为360.
19.(1)18,73
(2)
(3)
【分析】(1)根据频率分布直方图中数据计算所求人数,由每组区间的中点值乘以频率相加得平均值;
(2)先判断抽取的100名学生成绩的第50百分位数在内,再列方程求解即可;
(3)由频率分布直方图根据比例求出三个区间上的人数,然后利用排列组合思想,结合古典概型概率公式求解即可.
【详解】(1)成绩低于60分的人数为(人).
平均成绩.
(2)由直方图可知成绩在,,的学生频率和为,
所以抽取的100名学生成绩的第50百分位数在内,
设第50百分位数为,则,
即第50百分位数约.
(3)∵成绩在,,的学生人数所占比例为,
∴从成绩在,,的学生中应分别抽取3人,2人,1人.
6人排成一列,共有(种)方法.
成绩在的学生站在一起的方法有(种),
∴把6人排成一列,成绩在的学生站在一起的概率.
20.(1)患病者的人数为40,,;(2)31450;(3).
【分析】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为40人,由此能求出,.
(2)指标检测值不低于5的样本中,有患病者28人,未患病者9人,共37人,此地区该项身体指标检测值不低于5的从业者的人数.
(3)当时,在100个样本数据中,有12名患病者被误判为未患病,有9名未患病者被误判为患病者,由此能判断错误的概率.
【详解】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为.
,.
(2)由(1)可知,患病者的人数为,未患病的人数为,该项身体指标检测值不低于5的样本中,有患病者(人),未患病者(人),共37人.
故估计此地区该项身体指标检测值不低于5的从业者的人数为.
(3)当时,在100个样本数据中,有(名)患病者被误判为未患病,有(名)未患病者被误判为患病,
因此判断错误的概率为.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.假设第一次感染新冠病毒并且康复后3个月内二次感染的概率大约是0.03,在半年内二次感染的概率是0.5.若某人第一次感染新冠病毒康复后,已经过去了三个月一直身体健康,在未来三个月内此人二次感染的概率是( )
A.0.45 B.0.48. C.0.49 D.0.47.
2.七巧板又称七巧图,智慧板,是一种古老的中国传统智力玩具.据清代陆以湉《冷庐杂识》说:“宋黄伯思宴几图,以方几七,长段相参,衍为二十五体,变为六十八名.明严澈蝶几图,则又变通其制,以勾股之形,作三角相错形,如蝶翅.其式三,其制六,其数十有三,其变化之式,凡一百有余.近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.”如图是一个用七巧板拼成的三角形(其中①②为两块全等的小型等腰直角三角形;③为一块中型等腰直角三角形;④⑤为两块全等的大型等腰直角三角形;⑥为一块正方形;⑦为一块平行四边形).现从该三角形中任取一点,则此点取自阴影部分的概率为( )
A. B. C. D.
3.已知某厂的产品合格率为0.7,现抽出10件产品检查,则下列说法正确的是( )
A.合格产品少于7件 B.合格产品多于7件
C.合格产品正好是7件 D.合格产品可能是7件
4.随着我国经济社会加快发展,人们思想观念不断更新,女性在企业管理中占据着越来越重要的地位,2021年12月21日,国家统计局发布了《中国妇女发展纲要(2011—2020年)》终期统计监测报告.下图为2010—2020年企业职工董事和职工监事中女性所占比重条形统计图,根据此图,判断下列说法错误的是( )
A.2010—2020年企业职工董事中女性所占比重的平均值为35.0个百分点
B.2020年企业职工董事中女性比重比2010年提高2.2个百分点
C.2020年企业职工监事中女性比重比2010年提高3.0个百分点
D.2011年企业职工监事中女性比重与董事中女性比重的差最大
5.已知与满足,若的中位数为6,则的中位数为( )
A.6 B.12 C.15 D.24
6.七巧板,又称七巧图、智慧板,是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,到了明代基本定型,于明、清两代在民间广泛流传.某同学用边长为4 dm的正方形木板制作了一套七巧板,如图所示,包括5个等腰直角三角形,1个正方形和1个平行四边形.若该同学从5个三角形中任取出2个,则这2个三角形的面积之和不小于另外3个三角形面积之和的概率是( )
A. B. C. D.
7.如图所示是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这10天最低气温的第80百分位数是( )
A. B.0 C.1 D.2
8.为比较甲、乙两名学生的数学素养,对课程标准中规定的数学六大素养进行指标测验(指标值满分为5分,分值高者为优),根据测验情况绘制了如图所示的六大素养指标雷达图,则下面叙述正确的是( )
A.乙的数据分析素养优于甲 B.乙的数学建模素养优于数学抽象素养
C.甲的六大素养指标值波动性比乙小 D.甲的六大素养中直观想象最差
二、多选题
9.某校在开展的“体育节”活动中,为了解学生对“体育节”的满意程度,组织学生给活动打分(分数为整数,满分100分),发现分数均在内,从中随机抽取一个容量为300的样本,并将这些数据分成6组并作出样本的频率分布直方图,但不小心污损了部分图形(如图所示),则下列说法中正确的是( )
A.样本中分数落在的频数为45人 B.样本的众数为75分
C.样本的平均数为75分 D.样本的80百分位数为85分
10.某地区城乡居民储蓄存款年底余额(单位:亿元)变化情况如图所示,下列判断一定正确的是( )
A.该地区城乡居民储蓄存款年底余额总数逐年上升
B.到年农村居民存款年底总余额已超过了城镇居民存款年底总余额
C.城镇居民存款年底余额逐年下降
D.年城乡居民存款年底余额增长率大约为
11.2020年两会“部长通道”工信部部长表示,中国每周大概增加1万多个5G基站,4月份增加5G用户700多万人,5G通信将成为社会发展的关键动力,下图是某机构对我国未来十年5G用户规模的发展预测图.则( )
A.2022年我国5G用户规模年增长率最高
B.2022年我国5G用户规模年增长户数最多
C.从2020年到2026年,我国的5G用户规模增长两年后,其年增长率逐年下降
D.这十年我国的5G用户数规模,后5年的平均数与方差都分别大于前5年的平均数与方差
12.甲、乙两人下棋,和棋的概率为,乙获胜的概率为,则下列说法错误的是( )
A.甲获胜的概率是 B.甲不输的概率是
C.乙输的概率是 D.乙不输的概率是
三、填空题
13.《定理汇编》记载了诸多重要的几何定理,其中有一些定理是关于鞋匠刀形的,即由在同一直线上同侧的三个半圆所围成的图形,其被阿基米德称为鞋匠刀形.如图所示,三个半圆的圆心分别为,,,半径分别为,,(其中),在半圆О内随机取一点,此点取自图中鞋匠刀形(阴影部分)的概率为,则 .
14.《九章算术》第三章“衰分”中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱,欲以钱数多少衰出之,问各几何 ”其意为:“今有甲带了560钱,乙带了350钱,丙带了180钱,三人一起出关,共需要交关税100钱,依照钱的多少按比例出钱”,则乙应出(所得结果四舍五入,保留整数)钱数为 .
15.若样本数据是以频率分布直方图的形式给出,这时已不存在原始数据,因此要确定其p%分位数,只能估算,其p%分位数即为频率分布直方图中使左侧小矩形面积之和等于p%的分点值.
例如:若某校100名学生的数学测试成绩的频率分布直方图如图:则可估计其80%分位数为 .
16.对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为的数据不慎丢失,则依据此图可得:
(1)年龄组为对应小矩形的高度为 ;
(2)由频率分布直方图估计志愿者年龄的85%分位数为 岁(结果保留整数).
四、解答题
17.某山村海拔较高,交通极为不便,被称为“云端上的村庄”,系建档立卡贫困村.民政部门为此组建了精准扶贫队对该村进行定点帮扶,扶贫组在实地调研后,立足当地独特优势,大力发展乡村经济,带动全村父老乡亲脱贫奔小康.为了解贫困户的帮扶情况,该地民政部门从本村的贫困户中随机抽取100户对去年的年收入进行了一个抽样调查,得到如下表所示的频数表:
收入(千元)
频数 15 10 35 20 10 10
(1)估计本村的贫困户的年收入的众数、第75百分位数;
(2)用分层抽样的方法从这100户贫困户抽取20户贫困户进行帮扶,若再从抽样调查收入在和的贫困户中随机选取2户作为重点帮扶对象,求至少有一户来自收入在千元的概率;
18.某校为了解学生每日行走的步数,在全校3000名学生中随机抽取200名,给他们配发了计步手环,统计他们的日行步数,按步数分组,得到频率分布直方图如图所示,
(1)求的值,并求出这200名学生日行步数的样本众数、中位数、平均数;
(2)学校为了鼓励学生加强运动,决定对步数大于或等于13000步的学生加1分,计入期末三好学生评选的体育考核分,估计全校每天获得加分的人数.
19.中华人民共和国第十四届全国运动会、全国第十一届残运会暨第八届特奥会将于2021年在中国陕西举行.为宣传全运会、特奥会,让更多的人了解体育运动项目和体育精神,某大学举办了全运会、特奥会知识竞赛,并从中随机抽取了100名学生的成绩,绘制成如图所示的频率分布直方图.
(1)试根据频率分布直方图求出这100人中成绩低于60分的人数,并估计这100人的平均成绩(同一组数据用该组区间的中点值代替);
(2)求出随机抽取的100名学生成绩的第50百分位数(结果保留到小数点后一位);
(3)若采用分层抽样的方法从成绩在,,的学生中共抽取6人,把6人排成一列,求成绩在的学生站在一起的概率.
20.在某地区,某项职业的从业者共约8.5万人,其中约3.4万人患有某种职业病:为了解这种职业病与某项身体指标(检测值为不超过6的正整数)间的关系,依据是否患有职业病,使用分层抽样的方法随机抽取了100名从业者,记录他们该项身体指标的检测值,整理得到如下统计图:
(1)求样本中患病者的人数和图中a,b的值;
(2)试估计此地区该项身体指标检测值不低于5的从业者的人数;
(3)某研究机构提出,可以选取常数,若一名从业者该项身体指标检测值大于,则判定其患有这种职业病;若检测值小于,则判定其未患有这种职业病.从样本中随机选择一名从业者,按照这种方式判断其是否患病,求判断错误的概率.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.B
【分析】理解题意,康复后半年内感染的概率为康复后三个月感染的概率和康复后前三个月健康而未来三个月感染的概率之和,建立方程式解出即可.
【详解】令康复后前三个月健康而未来三个月内二次感染的概率为,
则可得:,
解得;
故选:B.
2.B
【分析】数形结合,通过对图形的各点标记,以及各块几何图的性质,进行边长运算即可得出结论.
【详解】如图,
为等腰直角三角形, 连接,
由题可知, 分别为的中点,
设,则,, , ,
则,
阴影部分②的面积为,
阴影部分⑦的面积为
则从该三角形中任取一点,则此点取自阴影部分的概率为,
故选:B.
3.D
【分析】根据概率的定义和性质直接求解即可.
【详解】根据概率的性质可计算出合格产品可能是件,
故选:D.
4.A
【分析】本题考查学生筛选整合信息,处理信息的能力。此类题要求学生在对题目内容的理解与辨析,找出文章条形统计图中相对应的信息并进行计算,即可得到结论.
【详解】解:2010—2020年企业职工董事中女性所占比重的平均值为个百分点,选项A错误;
2020年企业职工董事中女性比重比2010年提高34.9-32.7=2.2个百分点,选项B正确;
2020年企业职工监事中女性比重比2010年提高38.2-35.2=3.0个百分点,选项C正确;
2011年企业职工监事中女性比重与董事中女性比重的差最大,为4个百分点,选项D正确.
故选:A.
5.C
【分析】由于中,与 成正比,记 为的中位数,则中对应的中位数为.; 从而求出的中位数.
【详解】解:记 为的中位数,为中对应的中位数
因为,,
所以为
故选C.
6.D
【分析】先逐个求解所有5个三角形的面积,再根据要求计算概率.
【详解】如图所示,,,,,的面积分别为,,.
将,,,,分别记为,,,,,从这5个三角形中任取出2个,则样本空间,共有10个样本点.
记事件表示“从5个三角形中任取出2个,这2个三角形的面积之和不小于另外3个三角形面积之和”,则事件包含的样本点为,,,共3个,所以.
故选:D.
7.D
【分析】利用百分位数的定义即可得解;
【详解】由折线图可知,这10天的最低气温按照从小到大的顺序排列为:,,,,0,0,1,2,2,2,
因为共有10个数据,所以是整数,
则这10天最低气温的第80百分位数是.
故选:D
8.C
【分析】根据所给的六大素养雷达图逐个分析即可.
【详解】A选项,甲的数据分析素养为分, 乙的数据分析素养为分, 乙的数据分析素养低于甲,选项错误;
B选项,乙的数学建模素养为分, 乙的数学抽象为素养分,选项错误;
C选项, 甲的六大素养指标值分别为,,,,,;乙的六大素养指标值分别为,,,,,,甲的六大素养指标值波动性比乙小,选项正确;
D选项,由C可知,甲的六大素养中,数学抽象,数学建模和数学运算最差,直观想象最最好,选项错误;
故选C.
【点睛】本题考查了命题真假的判断以及统计图雷达图的识别和应用,考查学生简单的推理,属于基础题.
9.AB
【分析】根据频率分布直方图得到各组概率,根据概率和为1得到分数落在的频率进而求解其频数,从而判断A;根据频率最高的区间得到众数,从而判断B;根据频率分布直方图的平均数与百分位数求法计算,从而判断C和D.
【详解】设分数落在的频率为,
由题意得,各组频率依次为,,,,,,
所以,解得.
对于A,样本中分数落在的频数为人,故A正确;
对于B,由题意知,样本中的频率最高,所以众数为75分,故B正确;
对于C,样本的平均数为分,故C错误;
对于D,分数小于80的频率为,分数小于90的频率为,所以样本的80百分位数位于,设为,
则,解得,故D错误.
故选:AB
10.AD
【解析】结合扇形图与条形图分析对比,对选项逐一分析判断.
【详解】由条形图可知,余额总数逐年上升,故A项正确;由城乡储蓄构成百分比可知,年农村居民存款年底总余额占,城镇居民存款年底总余额占,没有超过,故B项错误;城镇居民存款年底余额所占的比重逐年下降,但城镇居民存款年底余额年,年,年分别为(亿元),(亿元),(亿元),总体不是逐年下降的,故C项错误,年城乡居民存款年底余额增长率大约为,故D项正确.
故选:AD.
11.AC
【分析】由图表中所给数据进行分析判断即可.
【详解】由图表可得,年5G用户规模年增长率最高,故A正确;
年5G用户规模年增长户数最多为(万人),故B错;
由图表可知,从年开始,年与年5G用户规模年增长率增加,从年开始到年5G用户规模年增长率逐年递减,故C正确;
由于后五年5G用户数增长不大,数据较稳定,故方差小于前5年数据方差,所以D错.
故选:AC.
【点睛】本题考查统计图表的运用,考查学生读图获取信息的能力,较简单.
12.BCD
【分析】由对立事件、互斥事件、并事件的概率计算公式代入计算,对选项逐一判断.
【详解】“甲获胜”是“和棋或乙获胜”的对立事件,所以“甲获胜”的概率是,故A正确;设甲不输为事件A,则事件A是“甲获胜”和“和棋”这两个互斥事件的并事件,所以,故B错误;“乙输”的概率即“甲获胜”的概率,为,故C错误;设乙不输为事件B,则事件B是“乙获胜”和“和棋”这两个互斥事件的并事件,所以,故D错误;
故选:BCD
13./
【分析】通过计算三个半圆的面积,表示阴影部分的面积,利用几何概型的概率计算公式即可得出答案.
【详解】解:阴影部分面积为:
由图可知:,所以
则,
因为在半圆О内随机取一点,此点取自图中鞋匠刀形(阴影部分)的概率为,
所以,
,即,则
解得:,因为,
所以.
故答案为:.
14.32
【分析】根据甲乙丙所带钱数,可以计算出所交关税在全部钱中的占比,根据该比例,可算出乙应出的钱数.
【详解】由题可知:甲乙丙所带钱数的总和为:560+350+180=1090,
故关税缴纳的比例为:,
所以:乙应该出钱:.
故答案为:32.
【点睛】本题考查分层抽样在实际问题中的应用,需要注意每层的抽样比例与整体的抽样比例相等.
15.133.3.
【解析】根据分位数的定义计算可得.
【详解】解析:分数在130以下的学生所占比例为.
在140以下的学生所占比例为.
因此,80%分位数一定位于内,由.
可以估计80%分位数为133.3.
答案:133.3.
【点睛】本题考查分位数的概念,属于基础题.
16. 0.04/ 39
【分析】(1)根据频率分布直方图的特征及图中数据,列等式计算即可;
(2)根据分位数的定义及题中数据计算可得出结果.
【详解】(1)设所对应小矩形的高度为,根据题意,
,计算得, ;
(2)根据分位数的定义,设志愿者年龄的85%分位数为x,则
解得.
故答案为:0.04;39.
17.(1)11,13.5;
(2).
【分析】(1)根据频数表求众数及百位数即可;
(2)根据分层抽样可得在和范围抽取的贫困户数分别为3户和2户,再利用古典概型计算概率即可.
【详解】(1)众数为;
由于前三组的频率之和为,
前四组的频率之和为
∴第75百分位数在第4组中,
设第75百分位数为,则有:,解得:,
即第75百分位数为13.5;
(2)由频数表及分层抽样可知在收入范围内抽取的户数为,在收入范围内抽取的户数,
记年收入在的3名贫困户分别为A,,,年收入在的2名贫困户分别为,,
则从中随机抽取2户的所有可能结果为:,,,,,,,,,共10种,
其中抽到至少有一名在的贫困户的可能结果:,,,,,,有7种,
故年收入在的贫困户至少有1人被抽到的概率:.
18.(1)的值为0.1,众数为千步,中位数为千步,平均数为9.44千步
(2)360
【分析】(1)结合频率分布直方图,根据概率之和为1求出的值,进而结合图求解样本众数、中位数、平均数;
(2)根据已知条件求出步数大于或等于13000步的学生的频率,从而估计全校每天获得加分的人数即可.
【详解】(1)根据频率分布直方图可知,各组频率依次为,,,,,,,,
所以,
解得;
因为组频率最高,所以样本众数为千步;
步数小于8的频率为,步数小于10的频率为,所以中位数在之间,记为x,
则,解得,
所以中位数为千步;
平均数为,
所以平均数为9.44千步.
(2)由表可知,大于或等于13000步的学生频率为,
将频率看作概率,
则全校每天获得加分的人数约为(人),
所以估计全校每天获得加分的人数为360.
19.(1)18,73
(2)
(3)
【分析】(1)根据频率分布直方图中数据计算所求人数,由每组区间的中点值乘以频率相加得平均值;
(2)先判断抽取的100名学生成绩的第50百分位数在内,再列方程求解即可;
(3)由频率分布直方图根据比例求出三个区间上的人数,然后利用排列组合思想,结合古典概型概率公式求解即可.
【详解】(1)成绩低于60分的人数为(人).
平均成绩.
(2)由直方图可知成绩在,,的学生频率和为,
所以抽取的100名学生成绩的第50百分位数在内,
设第50百分位数为,则,
即第50百分位数约.
(3)∵成绩在,,的学生人数所占比例为,
∴从成绩在,,的学生中应分别抽取3人,2人,1人.
6人排成一列,共有(种)方法.
成绩在的学生站在一起的方法有(种),
∴把6人排成一列,成绩在的学生站在一起的概率.
20.(1)患病者的人数为40,,;(2)31450;(3).
【分析】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为40人,由此能求出,.
(2)指标检测值不低于5的样本中,有患病者28人,未患病者9人,共37人,此地区该项身体指标检测值不低于5的从业者的人数.
(3)当时,在100个样本数据中,有12名患病者被误判为未患病,有9名未患病者被误判为患病者,由此能判断错误的概率.
【详解】(1)根据分层抽样原则,容量为100的样本中,患病者的人数为.
,.
(2)由(1)可知,患病者的人数为,未患病的人数为,该项身体指标检测值不低于5的样本中,有患病者(人),未患病者(人),共37人.
故估计此地区该项身体指标检测值不低于5的从业者的人数为.
(3)当时,在100个样本数据中,有(名)患病者被误判为未患病,有(名)未患病者被误判为患病,
因此判断错误的概率为.
答案第1页,共2页
答案第1页,共2页
