初中数学华师大版七年级上册3.3.1 单项式除以单项式课件 10张PPT
文档属性
| 名称 | 初中数学华师大版七年级上册3.3.1 单项式除以单项式课件 10张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 882.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 14:35:07 | ||
图片预览




文档简介
(共10张PPT)
项
单
项
式
除
以
式
单
回顾 & 思考
(a ≠ 0)
1、用字母表示幂的运算性质:
(3)
= ;
(1)
= ;
(2)
= ;
2、计算:
(1) a15÷a10 (2) a3n÷an
= a5
= a2n
n
n
b
a
3、计算
(1) 2x yz .3xy = (2)a b . ( )=3a b c
6x y z
3abc
(4)
由(1),(2)可得:
(3) 6x y z ÷ 3xy = 2x yz
(4) 3a b c÷ a b =3abc
观察、归纳
(3) 6x y z ÷ 3xy =(6÷3).(x3÷x).(y3÷y2).z2
=2x yz
(4) 3a b c ÷ a b = (3÷1).( a3÷a2).(b2÷b).c
=3abc
观察 & 归纳
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷ (除式的系数)
连同指数一起作为商的因式。
商式的系数=
单项式除以单项式,其结果(商式)仍是
只在被除式里含有的字母,
同底数幂(即相同的字母及指数),直接相除
一个单项式;
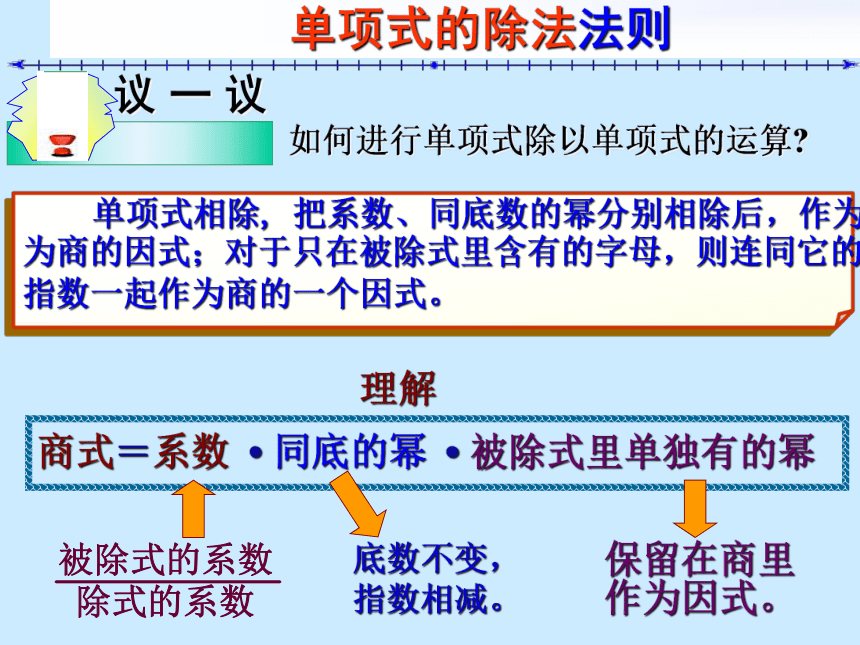
单项式的除法法则
如何进行单项式除以单项式的运算
议 一 议
单项式相除, 把系数、同底数的幂分别相除后,作为
为商的因式;对于只在被除式里含有的字母,则连同它的
指数一起作为商的一个因式。
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
例题解析
学一学
例1 计算:
(1) ; (2) -21a2b3c÷3ab;
24 a3b2
÷ 3 ab2
(3) (6 xy2)2 ÷ 3 xy
(4) 6a3(2a+b)4c2÷9a(2a+b)2
解:(1) 24 a3b2÷ 3 ab2
=8a2
(2)-21a2b3c÷ 3ab
= -7ab2c
(3)(6xy2)2÷ 3xy
=36x2y4÷ 3xy
=12xy3
(4) 6a3 (2a+b)4c2÷9a(2a+b)2
= a2(2a+b)2c2
注意:b2÷b2=1
=(24÷3).(a3÷a).(b2÷b2)
= a3-1(2a+b)4-2c2
随堂
练习
(1) 2a6b3÷a3b2 ; (2) ;
(3) (-2x2y)3÷(6x3y2) (4) (-2m3n2)4÷2m4n3. 3m2n
解:
1、计算:
( x3y2 z )
÷( x2y)
接综合练习
(1)2a6b3÷a3b2
=2a3b
(2)
( x3y2 z )
÷( x2y)
= xyz
(3) (-2x2y)3÷ 6x3y2
= -8x6y3÷6x3y2
= - x3y
3
4
(4) (-2m3n2)4÷2m4n3.3m2n
=16m12n8÷2m4n3.3m2n
=8m8n5.3m2n
=24m10n6
书上练习 2题
练一练
下雨时,常常是“先见闪电,后闻雷鸣”,这是因为光速
比声速快的缘故。已知光在空气中的传播速度约为3×108
米/秒,而声音在空气中的传播速度约为3.4×102 米/秒。
请计算一下,光速是声速的多少倍?(结果保留万位)
解:( 3×108)÷( 3.4×102)
=(3÷ 3.4)×108-2
≈0.88 ×106
=8.8 ×105
答:光速是声速的约8.8 ×105倍。
巩固练 习
1、计算填空:
⑴ 60x3y5 ÷( 12xy3) = ;
◣ ◢
综
(2) 8x6y4z ÷( ) = 4x2y2 ;
(3) ( )÷2x3y3 = ;
合
(4) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;
5x2y2
2x4y2z
12
3
2
本节课你的收获是什么?
同底数幂相除是单项式除法的特例;
在计算题时,要注意运算顺序和符号.
单项式除以单项式的法则
作业:
习题13.4
1题(1),(2),(3); 4题
项
单
项
式
除
以
式
单
回顾 & 思考
(a ≠ 0)
1、用字母表示幂的运算性质:
(3)
= ;
(1)
= ;
(2)
= ;
2、计算:
(1) a15÷a10 (2) a3n÷an
= a5
= a2n
n
n
b
a
3、计算
(1) 2x yz .3xy = (2)a b . ( )=3a b c
6x y z
3abc
(4)
由(1),(2)可得:
(3) 6x y z ÷ 3xy = 2x yz
(4) 3a b c÷ a b =3abc
观察、归纳
(3) 6x y z ÷ 3xy =(6÷3).(x3÷x).(y3÷y2).z2
=2x yz
(4) 3a b c ÷ a b = (3÷1).( a3÷a2).(b2÷b).c
=3abc
观察 & 归纳
商式
被除式
除式
仔细观察一下,并分析与思考下列几点:
(被除式的系数)÷ (除式的系数)
连同指数一起作为商的因式。
商式的系数=
单项式除以单项式,其结果(商式)仍是
只在被除式里含有的字母,
同底数幂(即相同的字母及指数),直接相除
一个单项式;
单项式的除法法则
如何进行单项式除以单项式的运算
议 一 议
单项式相除, 把系数、同底数的幂分别相除后,作为
为商的因式;对于只在被除式里含有的字母,则连同它的
指数一起作为商的一个因式。
理解
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减。
保留在商里
作为因式。
例题解析
学一学
例1 计算:
(1) ; (2) -21a2b3c÷3ab;
24 a3b2
÷ 3 ab2
(3) (6 xy2)2 ÷ 3 xy
(4) 6a3(2a+b)4c2÷9a(2a+b)2
解:(1) 24 a3b2÷ 3 ab2
=8a2
(2)-21a2b3c÷ 3ab
= -7ab2c
(3)(6xy2)2÷ 3xy
=36x2y4÷ 3xy
=12xy3
(4) 6a3 (2a+b)4c2÷9a(2a+b)2
= a2(2a+b)2c2
注意:b2÷b2=1
=(24÷3).(a3÷a).(b2÷b2)
= a3-1(2a+b)4-2c2
随堂
练习
(1) 2a6b3÷a3b2 ; (2) ;
(3) (-2x2y)3÷(6x3y2) (4) (-2m3n2)4÷2m4n3. 3m2n
解:
1、计算:
( x3y2 z )
÷( x2y)
接综合练习
(1)2a6b3÷a3b2
=2a3b
(2)
( x3y2 z )
÷( x2y)
= xyz
(3) (-2x2y)3÷ 6x3y2
= -8x6y3÷6x3y2
= - x3y
3
4
(4) (-2m3n2)4÷2m4n3.3m2n
=16m12n8÷2m4n3.3m2n
=8m8n5.3m2n
=24m10n6
书上练习 2题
练一练
下雨时,常常是“先见闪电,后闻雷鸣”,这是因为光速
比声速快的缘故。已知光在空气中的传播速度约为3×108
米/秒,而声音在空气中的传播速度约为3.4×102 米/秒。
请计算一下,光速是声速的多少倍?(结果保留万位)
解:( 3×108)÷( 3.4×102)
=(3÷ 3.4)×108-2
≈0.88 ×106
=8.8 ×105
答:光速是声速的约8.8 ×105倍。
巩固练 习
1、计算填空:
⑴ 60x3y5 ÷( 12xy3) = ;
◣ ◢
综
(2) 8x6y4z ÷( ) = 4x2y2 ;
(3) ( )÷2x3y3 = ;
合
(4) 若 (ax3my12)÷(3x3y2n)=4x6y8 ,
则 a = , m = ,n = ;
5x2y2
2x4y2z
12
3
2
本节课你的收获是什么?
同底数幂相除是单项式除法的特例;
在计算题时,要注意运算顺序和符号.
单项式除以单项式的法则
作业:
习题13.4
1题(1),(2),(3); 4题
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
