新人教A版必修第一册高中数学第四章 指数函数与对数函数 单元素养测评卷(含解析)
文档属性
| 名称 | 新人教A版必修第一册高中数学第四章 指数函数与对数函数 单元素养测评卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 151.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 16:23:36 | ||
图片预览
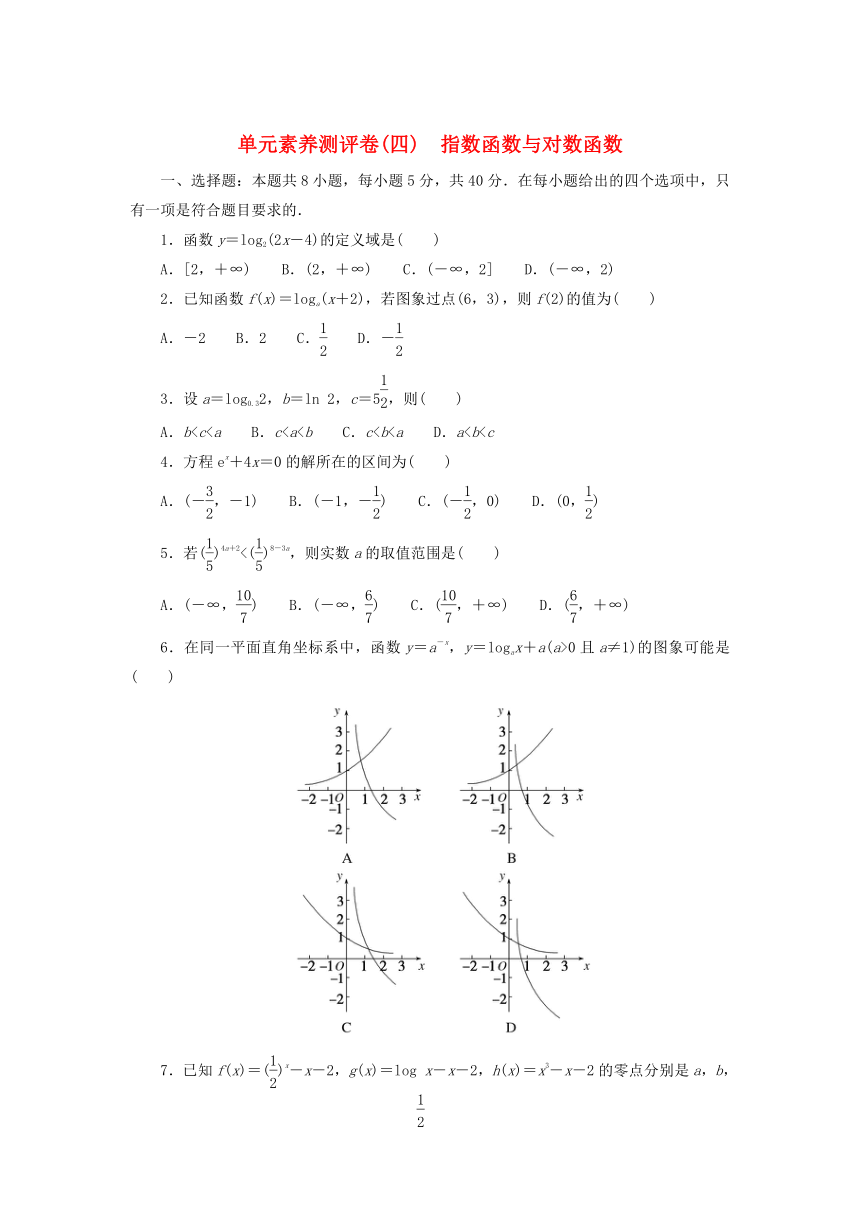




文档简介
单元素养测评卷(四) 指数函数与对数函数
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数y=log2(2x-4)的定义域是( )
A.[2,+∞) B.(2,+∞) C.(-∞,2] D.(-∞,2)
2.已知函数f(x)=loga(x+2),若图象过点(6,3),则f(2)的值为( )
A.-2 B.2 C. D.-
3.设a=log0.32,b=ln 2,c=5,则( )
A.b4.方程ex+4x=0的解所在的区间为( )
A.(-,-1) B.(-1,-) C.(-,0) D.(0,)
5.若()4a+2<()8-3a,则实数a的取值范围是( )
A.(-∞,) B.(-∞,) C.(,+∞) D.(,+∞)
6.在同一平面直角坐标系中,函数y=a-x,y=logax+a(a>0且a≠1)的图象可能是( )
7.已知f(x)=()x-x-2,g(x)=logx-x-2,h(x)=x3-x-2的零点分别是a,b,c,则a,b,c的大小顺序是( )
A.a>b>c B.c>b>a C.b>c>a D.b>a>c
8.已知函数f(x)=(a>0且a≠1)有最大值,则实数a的取值范围是( )
A.(0,] B.[4,+∞) C.[2,+∞) D.(0,]
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列正确的是( )
A.()2+=4
B.log89×log2732=
C.若a+a-1=3,则a2+a-2-=2
D.若3x=4y=M,且+=1,则M=36
10.下列结论中正确的是( )
A.函数y=2x-1是指数函数
B.若am>an(a>0,a≠1),则m>n
C.函数y=ax2+1(a>1)的值域是[1,+∞)
D.函数f(x)=ax-2-3(a>0,a≠1)的图象必过定点(2,-2)
11.已知函数y=-logax(a>0,a≠1)和y=()x(a>0,a≠1),以下结论正确的有( )
A.它们互为反函数
B.它们的定义域与值域正好互换
C.它们的单调性相反
D.它们的图象关于直线y=x对称
12.设函数f(x)=ln (2-x2),则( )
A.f(x)是偶函数 B.f(x)在(0,+∞)上单调递减
C.f(x)的最大值为ln 2 D.x=是f(x)的一个零点
三、填空题:本题共4小题,每小题5分,共20分.
13.函数f(x)=+的定义域为________.
14.已知函数f(x)=,则f(log26)=________.
15.函数y=log2(2x+2)的值域为________.
16.设函数f(x)=,若方程f(x)=b有且仅有1个实数根,则实数b的取值范围是________.
四、解答题:本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知函数f(x)=ax(a>0,且a≠1)的图象经过点(2,).
(1)求a的值;
(2)求f(x)在区间[-,1]上的最大值.
18.(12分)已知函数f(x)=kx+log2(2x+1)(k是常数且k∈R),且f(x)是偶函数.
(1)求k的值;
(2)若函数g(x)=f(x)+x-2,求函数y=g(x)的零点.
19.(12分)已知函数f(x)=.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并证明;
(3)解不等式f(x)≥4.
20.(12分)已知函数f(x)=loga(x-2)+loga(x-4)(a>0且a≠1).
(1)若a=2,且g(x)=f(x)-3,求函数g(x)的零点;
(2)当x∈(4,6]时,f(x)有最小值-3,求a的值.
21.(12分)近年来,得益于我国先进的运载火箭技术,我国在航天领域取得了巨大成就. 2022年11月29日,神舟十五号载人飞船搭载航天员费俊龙、邓清明、张陆飞往中国空间站,与神舟十四号航天员“会师”太空,12月4日晚神舟十四号载人飞船返回舱成功着陆,航天员陈冬、刘洋、蔡旭哲安全顺利出舱,圆满完成飞行任务. 据了解,在不考虑空气阻力和地球引力的理想状态下,可用公式v=v0ln 计算火箭的最大速度v(m/s),其中v0(m/s)是喷流相对速度,m(kg)是火箭(除推进剂外)的质量,M(kg)是推进剂与火箭质量的总和,称为“总质比”,已知A型火箭的喷流相对速度为500(m/s).
(1)当总质比为200时,利用给出的参考数据求A型火箭的最大速度;
(2)经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的2倍,总质比变为原来的,若要使火箭的最大速度至少增加500(m/s),求在材料更新和技术改进前总质比的最小整数值.
(参考数据:ln 2≈0.7,ln 5≈1.6,2.71822.(12分)已知函数f(x)=2x-+1.
(1)判断f(x)的单调性,并用定义证明;
(2)若关于x的方程f(2f(x))+f(t-4x)=0有解,求t的取值范围.
单元素养测评卷(四) 指数函数与对数函数
1.答案:B
解析:由已知得,2x-4>0,解得x>2,故x∈(2,+∞).故选B.
2.答案:B
解析:因为函数f(x)=loga(x+2)的图象过点(6,3),
所以loga(6+2)=3 loga8=logaa3,
则a3=8 a=2,
所以f(x)=log2(x+2),f(2)=log2(2+2)=2.故选B.
3.答案:D
解析:由对数函数性质知log0.32<0,01,
所以a4.答案:C
解析:令函数f(x)=ex+4x,则方程ex+4x=0的解即为函数f(x)的零点,而函数f(x)=ex+4x在R上单调递增,f(-)f(0)=1>0,因此函数f(x)的零点在区间(-,0)内,所以方程ex+4x=0的解所在的区间为(-,0).故选C.
5.答案:D
解析:因为函数y=()x是减函数,且()4a+2<()8-3a,
所以4a+2>8-3a,解得a>,即实数a的取值范围是(,+∞).故选D.
6.答案:A
解析:对于A,B,若y=a-x=()x图象正确,则0又x=1时,y=loga1+a=a>0,A正确,B错误;
对于C,D,若y=a-x=()x图象正确,则a>1,∴y=logax+a单调递增,CD错误.故选A.
7.答案:B
解析:函数f(x)=()x-x-2,g(x)=logx-x-2,h(x)=x3-x-2的零点,
即为函数y=x+2分别与函数y=()x,y=logx,y=x3的图象交点的横坐标,
如图所示:
由图可得a8.答案:D
解析:∵函数y=x+3在(-∞,3]上单调递增,
∴此时有最大值ymax=3+3=6,
∴要使f(x)有最大值,则需函数y=4+16ax(a>0且a≠1)在(3,+∞)上单调递减,
且4+16a3≤6,即,解得0∴a的取值范围是(0,].故选D.
9.答案:ABD
解析:A选项: ()2+=(22-)2+=22=4,故A正确;
B选项:log89×log2732=×=×=,故B正确;
C选项:a+a-1=3,a2+a-2-=(a+a-1)2-2-3×=1,故C错误;
D选项:3x=4y=M,则x=log3M,=logM3, 同理y=log4M,=logM4,则+=2logM3+logM4=logM36=1,解得M=36,故D正确.故选ABD.
10.答案:CD
解析:对于A项,函数y=2x-1的指数位置不符合指数函数,故A不正确.
对于B项,当0an时,m对于C项,∵a>1,x2≥0,∴ax2+1≥1,故函数y=ax2+1(a>1)的值域是[1,+∞),故C正确.
对于D项,∵∴,函数f(x)=ax-2-3(a>0,a≠1)的图象必过定点(2,-2),故D正确.
故选CD.
11.答案:ABD
解析:A选项,注意到y=-logax=logx,则其与函数y=()x互为反函数,故A正确;
B选项,函数y=logx定义域为(0,+∞),值域为R.函数y=()x定义域为R,值域为(0,+∞).故B正确;
C选项,当a>1时,两函数均在定义域内单调递减.当0D选项,两函数互为反函数,则函数图象关于直线y=x对称,故D正确.故选ABD.
12.答案:AC
解析:函数f(x)=ln (2-x2),由2-x2>0得f(x)的定义域为(-,),关于坐标原点对称,又f(-x)=f(x),所以f(x)为定义域上的偶函数,A选项正确;
令t=2-x2,则y=lnt,由二次函数的性质,当x∈(-,0)时,t=2-x2为增函数;当x∈(0,)时,t=2-x2为减函数;
y=lnt在定义域内为增函数,由复合函数的单调性可知,f(x)在(-,0)上单调递增,在(0,)上单调递减,B选项错误;
由函数单调性可知,f(x)最大值为f(0)=ln2,C选项正确;
ln (2-x2)=0,解得x=±1,则f(x)的零点为±1,D选项错误.故选AC.
13.答案:[0,2)∪(2,+∞)
解析:根据题意,由,解得x≥0且x≠2,因此定义域为[0,2)∪(2,+∞).
14.答案:6
解析:根据对数函数单调性可得:log26∈(2,3),
f(log26)==6.
15.答案:(1,+∞)
解析:函数的定义域为R,
令t=2x+2,则y=log2t,
因为2x>0,所以2x+2>2,即t>2,
所以log2t>log22=1,即y>1,
所以函数y=log2(2x+2)的值域为(1,+∞).
16.答案:(-∞,0]∪(,1]
解析:作出函数y=f(x)的图象,如图:
结合图象可得:b∈(-∞,0]∪(,1].
17.解析:(1)因为函数f(x)=ax(a>0,且a≠1)的图象经过点(2,),
所以a2=.
所以a=.
(2)因为a=,所以f(x)=()x.
所以f(x)在区间[-,1]上单调递减.
所以f(x)在区间[-,1]上的最大值是f(-).
所以f(-)=()-=.
所以f(x)在区间[-,1]上的最大值是.
18.解析:(1)f(x)=kx+log2(2x+1),函数定义域为R,
f(-x)=k·(-x)+log2(2-x+1)=k·(-x)+log2()=log2(2x+1)-(k+1)·x,
f(x)是偶函数,f(-x)=f(x),故k=-(k+1),解得k=-.
(2)由(1)可知,f(x)=-x+log2(2x+1),g(x)=f(x)+x-2=log2(2x+1)-2,令g(x)=log2(2x+1)-2=0,解得x=log23.
故函数y=g(x)零点为log23.
19.解析:(1)易知函数f(x)=,x∈R.
所以定义域为R.
(2)证明:由f(-x)===f(x),从而知f(x)为偶函数.
(3)由条件得≥4=22,得x2-1≥2,解得x≥或x≤-.
所以不等式的解集为{x|x≥或x≤-}.
20.解析:(1)a=2时,g(x)=log2(x-2)+log2(x-4)-3的定义域为(4,+∞),
令g(x)=log2(x-2)+log2(x-4)-3=0,
即log2[(x-2)(x-4)]=3,所以(x-2)(x-4)=8,
即x2-6x=0解得x=0(舍)或x=6.
所以g(x)的零点为6.
(2)f(x)=loga(x-2)+loga(x-4)=loga(x2-6x+8),x∈(4,6],
令y=x2-6x+8,x∈(4,6],
则y=x2-6x+8在x∈(4,6]上单调递增,
若0f(x)min=f(6)=loga8=-3解得a=,
若a>1,f(x)=loga(x2-6x+8)在x∈(4,6]上单调递增,
无最小值,不满足题意,所以a=.
21.解析:
(1)由已知可得v=500ln200=500(ln2+ln100)=500[ln2+2(ln2+ln5)]=500(3ln2+2ln5)≈2650m/s.
(2)设在材料更新和技术改进前总质比为x,且v1=v0lnx=500lnx,v2=1000ln,
若要使火箭的最大速度至少增加500m/s,所以v2-v1=1000ln-500lnx≥500,
即2ln-lnx≥1,ln ()2-lnx=ln≥1,所以≥e,解得x≥4e,因为2.71822.解析:
(1)f(x)在R上单调递增,证明如下:
易知f(x)的定义域为R,
设x1因为x1所以-<0,+1>0,+1>0,
所以f(x1)-f(x2)<0,则f(x)在R上单调递增.
(2)因为f(x)的定义域为R,且f(-x)+f(x)=-2x-+1+2x-+1=-+2=0,所以f(x)是奇函数.
由已知,方程f(2f(x))+f(t-4x)=0有解,
由f(x)的奇偶性可知f(2f(x))=f(4x-t)有解,
由f(x)的单调性可知2f(x)=4x-t有解,得方程-+2=-t有解,即方程-2=t有解.
因为ex+1∈(1,+∞),所以0<<1,则0<<4,
所以有-2<-2<2,故t的取值范围是(-2,2).
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.函数y=log2(2x-4)的定义域是( )
A.[2,+∞) B.(2,+∞) C.(-∞,2] D.(-∞,2)
2.已知函数f(x)=loga(x+2),若图象过点(6,3),则f(2)的值为( )
A.-2 B.2 C. D.-
3.设a=log0.32,b=ln 2,c=5,则( )
A.b
A.(-,-1) B.(-1,-) C.(-,0) D.(0,)
5.若()4a+2<()8-3a,则实数a的取值范围是( )
A.(-∞,) B.(-∞,) C.(,+∞) D.(,+∞)
6.在同一平面直角坐标系中,函数y=a-x,y=logax+a(a>0且a≠1)的图象可能是( )
7.已知f(x)=()x-x-2,g(x)=logx-x-2,h(x)=x3-x-2的零点分别是a,b,c,则a,b,c的大小顺序是( )
A.a>b>c B.c>b>a C.b>c>a D.b>a>c
8.已知函数f(x)=(a>0且a≠1)有最大值,则实数a的取值范围是( )
A.(0,] B.[4,+∞) C.[2,+∞) D.(0,]
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列正确的是( )
A.()2+=4
B.log89×log2732=
C.若a+a-1=3,则a2+a-2-=2
D.若3x=4y=M,且+=1,则M=36
10.下列结论中正确的是( )
A.函数y=2x-1是指数函数
B.若am>an(a>0,a≠1),则m>n
C.函数y=ax2+1(a>1)的值域是[1,+∞)
D.函数f(x)=ax-2-3(a>0,a≠1)的图象必过定点(2,-2)
11.已知函数y=-logax(a>0,a≠1)和y=()x(a>0,a≠1),以下结论正确的有( )
A.它们互为反函数
B.它们的定义域与值域正好互换
C.它们的单调性相反
D.它们的图象关于直线y=x对称
12.设函数f(x)=ln (2-x2),则( )
A.f(x)是偶函数 B.f(x)在(0,+∞)上单调递减
C.f(x)的最大值为ln 2 D.x=是f(x)的一个零点
三、填空题:本题共4小题,每小题5分,共20分.
13.函数f(x)=+的定义域为________.
14.已知函数f(x)=,则f(log26)=________.
15.函数y=log2(2x+2)的值域为________.
16.设函数f(x)=,若方程f(x)=b有且仅有1个实数根,则实数b的取值范围是________.
四、解答题:本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知函数f(x)=ax(a>0,且a≠1)的图象经过点(2,).
(1)求a的值;
(2)求f(x)在区间[-,1]上的最大值.
18.(12分)已知函数f(x)=kx+log2(2x+1)(k是常数且k∈R),且f(x)是偶函数.
(1)求k的值;
(2)若函数g(x)=f(x)+x-2,求函数y=g(x)的零点.
19.(12分)已知函数f(x)=.
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并证明;
(3)解不等式f(x)≥4.
20.(12分)已知函数f(x)=loga(x-2)+loga(x-4)(a>0且a≠1).
(1)若a=2,且g(x)=f(x)-3,求函数g(x)的零点;
(2)当x∈(4,6]时,f(x)有最小值-3,求a的值.
21.(12分)近年来,得益于我国先进的运载火箭技术,我国在航天领域取得了巨大成就. 2022年11月29日,神舟十五号载人飞船搭载航天员费俊龙、邓清明、张陆飞往中国空间站,与神舟十四号航天员“会师”太空,12月4日晚神舟十四号载人飞船返回舱成功着陆,航天员陈冬、刘洋、蔡旭哲安全顺利出舱,圆满完成飞行任务. 据了解,在不考虑空气阻力和地球引力的理想状态下,可用公式v=v0ln 计算火箭的最大速度v(m/s),其中v0(m/s)是喷流相对速度,m(kg)是火箭(除推进剂外)的质量,M(kg)是推进剂与火箭质量的总和,称为“总质比”,已知A型火箭的喷流相对速度为500(m/s).
(1)当总质比为200时,利用给出的参考数据求A型火箭的最大速度;
(2)经过材料更新和技术改进后,A型火箭的喷流相对速度提高到了原来的2倍,总质比变为原来的,若要使火箭的最大速度至少增加500(m/s),求在材料更新和技术改进前总质比的最小整数值.
(参考数据:ln 2≈0.7,ln 5≈1.6,2.718
(1)判断f(x)的单调性,并用定义证明;
(2)若关于x的方程f(2f(x))+f(t-4x)=0有解,求t的取值范围.
单元素养测评卷(四) 指数函数与对数函数
1.答案:B
解析:由已知得,2x-4>0,解得x>2,故x∈(2,+∞).故选B.
2.答案:B
解析:因为函数f(x)=loga(x+2)的图象过点(6,3),
所以loga(6+2)=3 loga8=logaa3,
则a3=8 a=2,
所以f(x)=log2(x+2),f(2)=log2(2+2)=2.故选B.
3.答案:D
解析:由对数函数性质知log0.32<0,0
所以a
解析:令函数f(x)=ex+4x,则方程ex+4x=0的解即为函数f(x)的零点,而函数f(x)=ex+4x在R上单调递增,f(-)
5.答案:D
解析:因为函数y=()x是减函数,且()4a+2<()8-3a,
所以4a+2>8-3a,解得a>,即实数a的取值范围是(,+∞).故选D.
6.答案:A
解析:对于A,B,若y=a-x=()x图象正确,则0
对于C,D,若y=a-x=()x图象正确,则a>1,∴y=logax+a单调递增,CD错误.故选A.
7.答案:B
解析:函数f(x)=()x-x-2,g(x)=logx-x-2,h(x)=x3-x-2的零点,
即为函数y=x+2分别与函数y=()x,y=logx,y=x3的图象交点的横坐标,
如图所示:
由图可得a
解析:∵函数y=x+3在(-∞,3]上单调递增,
∴此时有最大值ymax=3+3=6,
∴要使f(x)有最大值,则需函数y=4+16ax(a>0且a≠1)在(3,+∞)上单调递减,
且4+16a3≤6,即,解得0
9.答案:ABD
解析:A选项: ()2+=(22-)2+=22=4,故A正确;
B选项:log89×log2732=×=×=,故B正确;
C选项:a+a-1=3,a2+a-2-=(a+a-1)2-2-3×=1,故C错误;
D选项:3x=4y=M,则x=log3M,=logM3, 同理y=log4M,=logM4,则+=2logM3+logM4=logM36=1,解得M=36,故D正确.故选ABD.
10.答案:CD
解析:对于A项,函数y=2x-1的指数位置不符合指数函数,故A不正确.
对于B项,当0
对于D项,∵∴,函数f(x)=ax-2-3(a>0,a≠1)的图象必过定点(2,-2),故D正确.
故选CD.
11.答案:ABD
解析:A选项,注意到y=-logax=logx,则其与函数y=()x互为反函数,故A正确;
B选项,函数y=logx定义域为(0,+∞),值域为R.函数y=()x定义域为R,值域为(0,+∞).故B正确;
C选项,当a>1时,两函数均在定义域内单调递减.当0
12.答案:AC
解析:函数f(x)=ln (2-x2),由2-x2>0得f(x)的定义域为(-,),关于坐标原点对称,又f(-x)=f(x),所以f(x)为定义域上的偶函数,A选项正确;
令t=2-x2,则y=lnt,由二次函数的性质,当x∈(-,0)时,t=2-x2为增函数;当x∈(0,)时,t=2-x2为减函数;
y=lnt在定义域内为增函数,由复合函数的单调性可知,f(x)在(-,0)上单调递增,在(0,)上单调递减,B选项错误;
由函数单调性可知,f(x)最大值为f(0)=ln2,C选项正确;
ln (2-x2)=0,解得x=±1,则f(x)的零点为±1,D选项错误.故选AC.
13.答案:[0,2)∪(2,+∞)
解析:根据题意,由,解得x≥0且x≠2,因此定义域为[0,2)∪(2,+∞).
14.答案:6
解析:根据对数函数单调性可得:log26∈(2,3),
f(log26)==6.
15.答案:(1,+∞)
解析:函数的定义域为R,
令t=2x+2,则y=log2t,
因为2x>0,所以2x+2>2,即t>2,
所以log2t>log22=1,即y>1,
所以函数y=log2(2x+2)的值域为(1,+∞).
16.答案:(-∞,0]∪(,1]
解析:作出函数y=f(x)的图象,如图:
结合图象可得:b∈(-∞,0]∪(,1].
17.解析:(1)因为函数f(x)=ax(a>0,且a≠1)的图象经过点(2,),
所以a2=.
所以a=.
(2)因为a=,所以f(x)=()x.
所以f(x)在区间[-,1]上单调递减.
所以f(x)在区间[-,1]上的最大值是f(-).
所以f(-)=()-=.
所以f(x)在区间[-,1]上的最大值是.
18.解析:(1)f(x)=kx+log2(2x+1),函数定义域为R,
f(-x)=k·(-x)+log2(2-x+1)=k·(-x)+log2()=log2(2x+1)-(k+1)·x,
f(x)是偶函数,f(-x)=f(x),故k=-(k+1),解得k=-.
(2)由(1)可知,f(x)=-x+log2(2x+1),g(x)=f(x)+x-2=log2(2x+1)-2,令g(x)=log2(2x+1)-2=0,解得x=log23.
故函数y=g(x)零点为log23.
19.解析:(1)易知函数f(x)=,x∈R.
所以定义域为R.
(2)证明:由f(-x)===f(x),从而知f(x)为偶函数.
(3)由条件得≥4=22,得x2-1≥2,解得x≥或x≤-.
所以不等式的解集为{x|x≥或x≤-}.
20.解析:(1)a=2时,g(x)=log2(x-2)+log2(x-4)-3的定义域为(4,+∞),
令g(x)=log2(x-2)+log2(x-4)-3=0,
即log2[(x-2)(x-4)]=3,所以(x-2)(x-4)=8,
即x2-6x=0解得x=0(舍)或x=6.
所以g(x)的零点为6.
(2)f(x)=loga(x-2)+loga(x-4)=loga(x2-6x+8),x∈(4,6],
令y=x2-6x+8,x∈(4,6],
则y=x2-6x+8在x∈(4,6]上单调递增,
若0
若a>1,f(x)=loga(x2-6x+8)在x∈(4,6]上单调递增,
无最小值,不满足题意,所以a=.
21.解析:
(1)由已知可得v=500ln200=500(ln2+ln100)=500[ln2+2(ln2+ln5)]=500(3ln2+2ln5)≈2650m/s.
(2)设在材料更新和技术改进前总质比为x,且v1=v0lnx=500lnx,v2=1000ln,
若要使火箭的最大速度至少增加500m/s,所以v2-v1=1000ln-500lnx≥500,
即2ln-lnx≥1,ln ()2-lnx=ln≥1,所以≥e,解得x≥4e,因为2.718
(1)f(x)在R上单调递增,证明如下:
易知f(x)的定义域为R,
设x1
所以f(x1)-f(x2)<0,则f(x)在R上单调递增.
(2)因为f(x)的定义域为R,且f(-x)+f(x)=-2x-+1+2x-+1=-+2=0,所以f(x)是奇函数.
由已知,方程f(2f(x))+f(t-4x)=0有解,
由f(x)的奇偶性可知f(2f(x))=f(4x-t)有解,
由f(x)的单调性可知2f(x)=4x-t有解,得方程-+2=-t有解,即方程-2=t有解.
因为ex+1∈(1,+∞),所以0<<1,则0<<4,
所以有-2<-2<2,故t的取值范围是(-2,2).
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
