5.圆4.扇形同步练习(含解析)人教版六年级数学上册
文档属性
| 名称 | 5.圆4.扇形同步练习(含解析)人教版六年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 464.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 15:41:11 | ||
图片预览




文档简介
5.圆 4.扇形同步练习 (含答案)人教版 六年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.已知圆形纸片的直径是10cm,将这个圆形纸片沿直径连续对折三次,得到的扇形的圆心角是( )°,面积是( )cm2。
2.下图中( )是圆心角。
3.下图中,阴影部分的面积是整个圆面积的,阴影部分的圆心角是( )度。
4.一个半径2分米的扇形周长7.14分米,这个扇形的圆心角是( )度。
二、选择题
5.把一张直径是4厘米的圆形纸片对折两次得到一个扇形,这个扇形的周长是( )厘米。
A.4+π B.4π C.π D.2+π
6.一只挂钟的时针长1dm,从上午9时到下午3时,时针尖端所走的路程是( )dm。
A.1.57 B.3.14 C.6.28 D.5.14
7.下面图形中的阴影部分是扇形的有( )个。
A.1 B.2 C.3 D.4
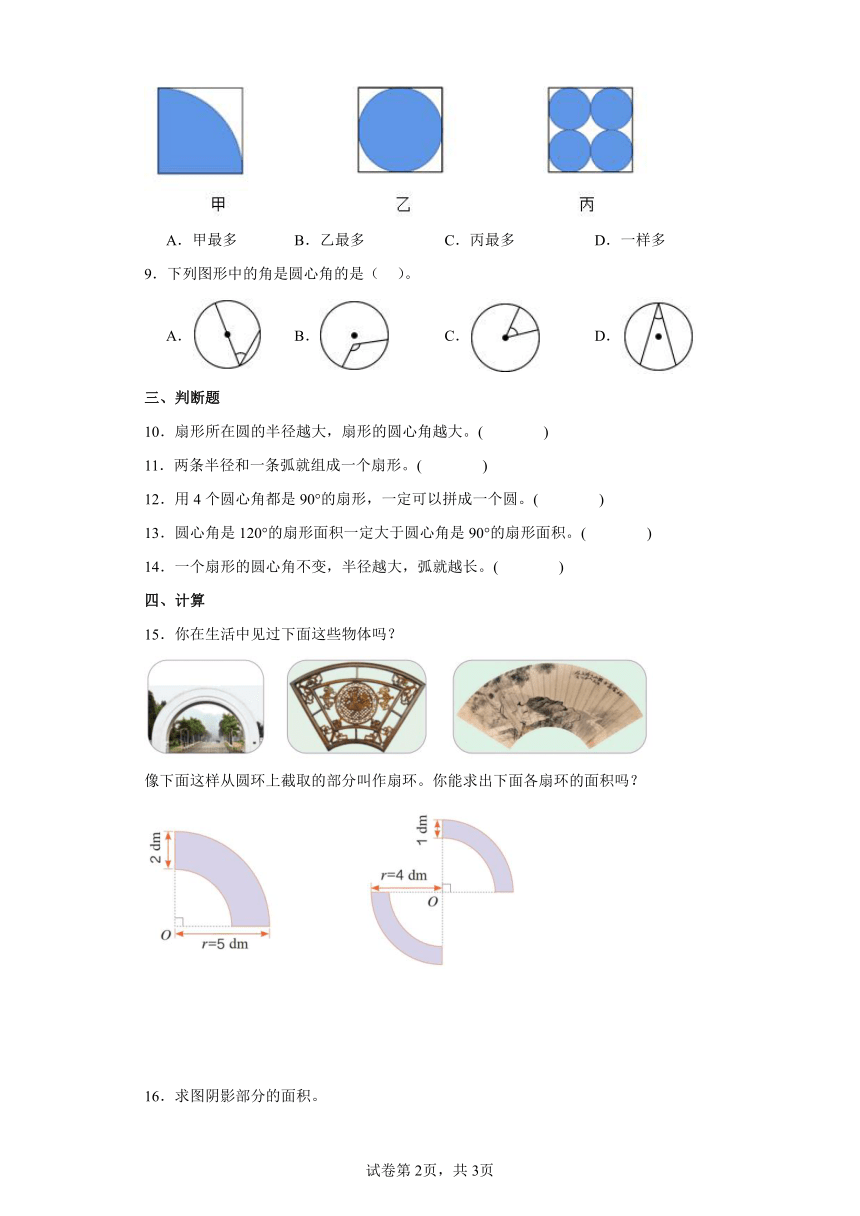
8.如图,甲、乙、丙三位同学用相同的正方形卡纸剪图形,甲剪了一个最大的扇形,乙剪了一个最大的圆,丙剪了四个最大的圆,三个人剩下的卡纸( )。
A.甲最多 B.乙最多 C.丙最多 D.一样多
9.下列图形中的角是圆心角的是( )。
A. B. C. D.
三、判断题
10.扇形所在圆的半径越大,扇形的圆心角越大。( )
11.两条半径和一条弧就组成一个扇形。( )
12.用4个圆心角都是90°的扇形,一定可以拼成一个圆。( )
13.圆心角是120°的扇形面积一定大于圆心角是90°的扇形面积。( )
14.一个扇形的圆心角不变,半径越大,弧就越长。( )
四、计算
15.你在生活中见过下面这些物体吗?
像下面这样从圆环上截取的部分叫作扇环。你能求出下面各扇环的面积吗?
16.求图阴影部分的面积。
五、解答题
17.在一个长8米宽6米的长方形花圃中,建了一个最大的圆形花坛。
(1)请在左图中画出这个圆形花坛。
(2)这个圆形花坛的面积为多少平方米?
(3)圆形花坛中有一个扇形区域种郁金香,这个扇形的圆心角是105度,请在图中画出郁金香的种植区域,并标出圆心角的度数。
18.如图,一个图形的中间是边长为1cm的正方形,四周是四个圆心角为90°的扇形,整个图形的面积是多少?
19.如下图,利用两面墙作边,用栅栏围成一个扇形羊圈。已知羊圈的直径是10米,则围成的羊圈面积是多少平方米?至少需要多少米长的栅栏?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 45 9.8125
【分析】对折三次之后是将360°平均分成8份,用360°÷8,求出扇形圆心角;再根据扇形的面积公式:面积=πr2×代入数据,即可解答。
【详解】360°÷8=45°
3.14×(10÷2)2×
=3.14×52×
=3.14×25×
=78.5×
=9.8125(cm2)
已知圆形纸片的直径是10cm,将这个圆形纸片沿直径连续对折三次,得到的扇形的圆心角是45°,面积是9.8125cm2。
【点睛】解答本题的关键是明确折叠三次就是把这个圆平均分成的份数,以及扇形面积公式的应用。
2.∠COD
【分析】顶点在圆心上,且角的两边是圆的两条半径,这样的角叫做圆心角。
观察图形可知,点A、B、C、D都不在圆心上,只有点O在圆心上,据此找到圆心角。
【详解】图中,只有∠COD的顶点O在圆心上,所以∠COD是圆心角。
【点睛】本题考查圆心角的认识,注意圆心角的顶点一定在圆心上。
3.60
【分析】周角360度,阴影部分是个扇形,将周角度数看作单位“1”,周角度数×扇形对应百分率=圆心角度数,据此列式计算。
【详解】360×=60(度),阴影部分的圆心角是60度。
【点睛】关键是理解分数乘法的意义,熟悉扇形的特征。
4.90
【分析】根据扇形的周长公式:可知,设圆心角为n,所以可以用扇形周长减两条半径之差乘上180°,再除以一条半径和3.14的乘积,即可列式为:(7.14-2×2)×180°÷2×3.14,据此解答。
【详解】(7.14-2×2)×180°÷(2×3.14)
=(7.14-4)×180°÷6.28
=3.14×180°÷6.28
=565.2°÷6.28
=90(度)
这个扇形的圆心角是90度。
【点睛】此题考查了扇形的周长公式。要求熟练掌握并灵活运用。
5.A
【分析】直径是4厘米的圆形纸片对折两次得到一个扇形,扇形大小是以4厘米为直径的圆的,这个扇形的周长为圆的周长的再加上两个半径,根据圆的周长公式C=πd,计算求解即可。
【详解】4+4π×=(4+π)厘米
所以把一张直径是4厘米的圆形纸片对折两次得到一个扇形,这个扇形的周长是(4+π)厘米。
故答案为:A
【点睛】明确圆形纸片对折两次后得到的扇形是一个的圆形,掌握扇形周长的计算方法是解题的关键。
6.B
【分析】下午3时转换成24小时计时法是3+12=15时,从9时到15时经过了15-9=6小时,时针每小时走一个格子是30°,6小时走过6×30=180°,时针走过的路程就是一个半径为1dm,圆心角为180°的圆弧的长度,也是圆的周长的一半。
【详解】3.14×2×1×
=6.28×
=3.14(分米)
时针尖端所走的路程是3.14分米。
故答案为:B
【点睛】此题主要考查弧长的求法,掌握24小时计时法与普通计时法的互化也是解题的关键。
7.C
【分析】由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形。
【详解】是扇形的有,共3个。
故答案为:C
【点睛】关键是熟悉扇形的特征,扇形是圆的一部分。
8.D
【分析】假设出正方形的边长,甲中扇形的半径等于正方形的边长,乙中圆的半径等于正方形边长的一半,丙中小圆的半径等于正方形边长的,利用“”分别求出三位同学所剪图形的面积,所剪的图形面积越大剩下的卡纸面积越小,所剪的图形面积相等时剩下卡纸的面积也相等,所剪的图形面积越小剩下的卡纸面积越大,据此解答。
【详解】假设正方形的边长为2。
甲:
=
=
乙:
=
=
丙:
=
=
=
由上可知,甲、乙、丙三位同学剪的图形面积相等,所以三个人剩下的卡纸一样多。
故答案为:D
【点睛】熟练掌握圆的面积计算公式并求出三个图形的面积是解答题目的关键。
9.C
【分析】根据圆心角的含义:顶点在圆心上的角叫做圆心角;据此解答即可。
【详解】A.顶点不在圆心,不是圆心角;
B.顶点不在圆心,不是圆心角;
C.顶点在圆心,是圆心角;
D.顶点不在圆心,不是圆心角;
故答案为:C
【点睛】此题主要考查了圆心角的含义,注意基础知识的积累。
10.×
【分析】角的大小与角的张口的大小有关,与边的长短无关。扇形所在圆的半径的长短,不影响圆心角的大小。
【详解】扇形所在圆的半径越大,扇形的圆心角不一定越大。如下图:
故答案为:×
【点睛】扇形的圆心角的大小与张口的大小有关,与半径的长短无关。
11.×
【详解】一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。如下图,根据扇形的意义可知,围成扇形的两条半径OA、0B必须经过弧AB的两端,不是任意的两条半径和一条弧就组成一个扇形,所以原题说法错误。
故答案为:×
12.×
【分析】一个圆形可以平均分成4个半径相等、圆心角都是90°的扇形。4个圆心角都是90°的扇形,它们的半径不一定相等,不一定可以拼成一个圆形,据此解答。
【详解】由分析可知:用4个圆心角都是90°且半径相等的扇形,一定可以拼成一个圆。题目中未说明4个扇形半径是否相等,因此不一定能拼成一个圆。
故答案为:×
【点睛】扇形的大小不仅与圆心角有关,也与扇形的半径有关。
13.×
【分析】扇形的面积=πr2×,据此分析。
【详解】扇形的面积除了与圆心角的大小有关,还与半径的长短有关系,所以原题说法错误。
故答案为:×
【点睛】关键是掌握并灵活运用扇形面积公式。
14.√
【分析】根据弧长=2πr×,可知弧长不仅与半径长度有关,还与它所对的圆心角的度数大小有关。一个因数不变,另一个因数扩大到原来的几倍或缩小到原来的几分之一(0除外),积也扩大到原来几倍或缩小到原来的几分之一;据此解答。
【详解】根据分析可知,一个扇形的圆心角不变,半径越大,弧就越长。此说法正确。
故答案为:√
【点睛】此题考查了弧长公式的灵活应用。
15.12.56;10.99
【分析】圆环的面积=,其中R指的是外圆的半径,r指的是内圆的半径,第一个扇环占整个圆环的,所以用圆环的面积乘,就是第一个扇环的面积;第二个扇环相当于圆环的面积,所以用圆环的面积乘就是这个扇环的面积。
【详解】(1)5-2=3(dm)
=
=50.24()
(2)4-1=3(dm)
=
=10.99()
16.13.76平方厘米
【分析】观察题意可知,空白部分的面积相当于一个直径是8厘米的圆面积,阴影部分的面积等于一个边长为8厘米的正方形面积减去空白部分的面积,根据正方形的面积公式和圆面积公式,代入数据分别求出正方形的面积和空白部分的面积,最后求出它们的差即可。
【详解】8÷2=4(厘米)
8×8-3.14×42
=8×8-3.14×16
=64-50.24
=13.76(平方厘米)
阴影部分的面积是13.76平方厘米。
17.(1)见详解;(2)28.26;(3)见详解
【分析】(1)根据题意,画出的圆的直径是6米。在长方形内找出一个合适的点作为圆心,取半径3米,画出这个圆;
(2)圆面积=3.14×半径2,据此列式求出这个圆的面积;
(3)以圆心为顶点,利用量角器画出一个105度的角,延长角的两边和圆周相交,画出扇形。
【详解】
(2)6÷2=3(米)
3.14×32=28.26(平方米)
所以,这个圆形花坛的面积为28.26平方米。
(1)(3)如图:
【点睛】本题考查了画圆及扇形、圆的面积,掌握圆和扇形的作图方法、圆的面积公式是解题的关键。
18.4.14平方厘米
【分析】根据题干可得:中间边长为1厘米的正方形,四周连接的圆心角90°扇形的半径也为1厘米,这四个圆心角为90°的扇形可拼接为一个半径1厘米的圆,根据圆面积=πr2,再加上正方形面积=边长×边长,可得出答案。
【详解】图形面积为:
(平方厘米)
答:整个图形的面积是4.14平方厘米。
【点睛】本题主要考查的是圆面积及正方形面积的应用,解题的关键是理解图形四周的圆心角90°扇形可以拼接成一个圆,进而计算得出答案。
19.58.875平方米;23.55米
【分析】由图可知,羊圈的面积占整个圆面积的,需要栅栏的长度占整个圆周长的,利用“”“”分别求出羊圈的面积和需要栅栏的长度,据此解答。
【详解】3.14×(10÷2)2×
=3.14×25×
=78.5×0.75
=58.875(平方米)
3.14×10×
=31.4×0.75
=23.55(米)
答:围成的羊圈面积是58.875平方米,至少需要23.55米长的栅栏。
【点睛】本题主要考查圆的周长和面积公式的应用,熟记公式是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.已知圆形纸片的直径是10cm,将这个圆形纸片沿直径连续对折三次,得到的扇形的圆心角是( )°,面积是( )cm2。
2.下图中( )是圆心角。
3.下图中,阴影部分的面积是整个圆面积的,阴影部分的圆心角是( )度。
4.一个半径2分米的扇形周长7.14分米,这个扇形的圆心角是( )度。
二、选择题
5.把一张直径是4厘米的圆形纸片对折两次得到一个扇形,这个扇形的周长是( )厘米。
A.4+π B.4π C.π D.2+π
6.一只挂钟的时针长1dm,从上午9时到下午3时,时针尖端所走的路程是( )dm。
A.1.57 B.3.14 C.6.28 D.5.14
7.下面图形中的阴影部分是扇形的有( )个。
A.1 B.2 C.3 D.4
8.如图,甲、乙、丙三位同学用相同的正方形卡纸剪图形,甲剪了一个最大的扇形,乙剪了一个最大的圆,丙剪了四个最大的圆,三个人剩下的卡纸( )。
A.甲最多 B.乙最多 C.丙最多 D.一样多
9.下列图形中的角是圆心角的是( )。
A. B. C. D.
三、判断题
10.扇形所在圆的半径越大,扇形的圆心角越大。( )
11.两条半径和一条弧就组成一个扇形。( )
12.用4个圆心角都是90°的扇形,一定可以拼成一个圆。( )
13.圆心角是120°的扇形面积一定大于圆心角是90°的扇形面积。( )
14.一个扇形的圆心角不变,半径越大,弧就越长。( )
四、计算
15.你在生活中见过下面这些物体吗?
像下面这样从圆环上截取的部分叫作扇环。你能求出下面各扇环的面积吗?
16.求图阴影部分的面积。
五、解答题
17.在一个长8米宽6米的长方形花圃中,建了一个最大的圆形花坛。
(1)请在左图中画出这个圆形花坛。
(2)这个圆形花坛的面积为多少平方米?
(3)圆形花坛中有一个扇形区域种郁金香,这个扇形的圆心角是105度,请在图中画出郁金香的种植区域,并标出圆心角的度数。
18.如图,一个图形的中间是边长为1cm的正方形,四周是四个圆心角为90°的扇形,整个图形的面积是多少?
19.如下图,利用两面墙作边,用栅栏围成一个扇形羊圈。已知羊圈的直径是10米,则围成的羊圈面积是多少平方米?至少需要多少米长的栅栏?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. 45 9.8125
【分析】对折三次之后是将360°平均分成8份,用360°÷8,求出扇形圆心角;再根据扇形的面积公式:面积=πr2×代入数据,即可解答。
【详解】360°÷8=45°
3.14×(10÷2)2×
=3.14×52×
=3.14×25×
=78.5×
=9.8125(cm2)
已知圆形纸片的直径是10cm,将这个圆形纸片沿直径连续对折三次,得到的扇形的圆心角是45°,面积是9.8125cm2。
【点睛】解答本题的关键是明确折叠三次就是把这个圆平均分成的份数,以及扇形面积公式的应用。
2.∠COD
【分析】顶点在圆心上,且角的两边是圆的两条半径,这样的角叫做圆心角。
观察图形可知,点A、B、C、D都不在圆心上,只有点O在圆心上,据此找到圆心角。
【详解】图中,只有∠COD的顶点O在圆心上,所以∠COD是圆心角。
【点睛】本题考查圆心角的认识,注意圆心角的顶点一定在圆心上。
3.60
【分析】周角360度,阴影部分是个扇形,将周角度数看作单位“1”,周角度数×扇形对应百分率=圆心角度数,据此列式计算。
【详解】360×=60(度),阴影部分的圆心角是60度。
【点睛】关键是理解分数乘法的意义,熟悉扇形的特征。
4.90
【分析】根据扇形的周长公式:可知,设圆心角为n,所以可以用扇形周长减两条半径之差乘上180°,再除以一条半径和3.14的乘积,即可列式为:(7.14-2×2)×180°÷2×3.14,据此解答。
【详解】(7.14-2×2)×180°÷(2×3.14)
=(7.14-4)×180°÷6.28
=3.14×180°÷6.28
=565.2°÷6.28
=90(度)
这个扇形的圆心角是90度。
【点睛】此题考查了扇形的周长公式。要求熟练掌握并灵活运用。
5.A
【分析】直径是4厘米的圆形纸片对折两次得到一个扇形,扇形大小是以4厘米为直径的圆的,这个扇形的周长为圆的周长的再加上两个半径,根据圆的周长公式C=πd,计算求解即可。
【详解】4+4π×=(4+π)厘米
所以把一张直径是4厘米的圆形纸片对折两次得到一个扇形,这个扇形的周长是(4+π)厘米。
故答案为:A
【点睛】明确圆形纸片对折两次后得到的扇形是一个的圆形,掌握扇形周长的计算方法是解题的关键。
6.B
【分析】下午3时转换成24小时计时法是3+12=15时,从9时到15时经过了15-9=6小时,时针每小时走一个格子是30°,6小时走过6×30=180°,时针走过的路程就是一个半径为1dm,圆心角为180°的圆弧的长度,也是圆的周长的一半。
【详解】3.14×2×1×
=6.28×
=3.14(分米)
时针尖端所走的路程是3.14分米。
故答案为:B
【点睛】此题主要考查弧长的求法,掌握24小时计时法与普通计时法的互化也是解题的关键。
7.C
【分析】由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形。
【详解】是扇形的有,共3个。
故答案为:C
【点睛】关键是熟悉扇形的特征,扇形是圆的一部分。
8.D
【分析】假设出正方形的边长,甲中扇形的半径等于正方形的边长,乙中圆的半径等于正方形边长的一半,丙中小圆的半径等于正方形边长的,利用“”分别求出三位同学所剪图形的面积,所剪的图形面积越大剩下的卡纸面积越小,所剪的图形面积相等时剩下卡纸的面积也相等,所剪的图形面积越小剩下的卡纸面积越大,据此解答。
【详解】假设正方形的边长为2。
甲:
=
=
乙:
=
=
丙:
=
=
=
由上可知,甲、乙、丙三位同学剪的图形面积相等,所以三个人剩下的卡纸一样多。
故答案为:D
【点睛】熟练掌握圆的面积计算公式并求出三个图形的面积是解答题目的关键。
9.C
【分析】根据圆心角的含义:顶点在圆心上的角叫做圆心角;据此解答即可。
【详解】A.顶点不在圆心,不是圆心角;
B.顶点不在圆心,不是圆心角;
C.顶点在圆心,是圆心角;
D.顶点不在圆心,不是圆心角;
故答案为:C
【点睛】此题主要考查了圆心角的含义,注意基础知识的积累。
10.×
【分析】角的大小与角的张口的大小有关,与边的长短无关。扇形所在圆的半径的长短,不影响圆心角的大小。
【详解】扇形所在圆的半径越大,扇形的圆心角不一定越大。如下图:
故答案为:×
【点睛】扇形的圆心角的大小与张口的大小有关,与半径的长短无关。
11.×
【详解】一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。如下图,根据扇形的意义可知,围成扇形的两条半径OA、0B必须经过弧AB的两端,不是任意的两条半径和一条弧就组成一个扇形,所以原题说法错误。
故答案为:×
12.×
【分析】一个圆形可以平均分成4个半径相等、圆心角都是90°的扇形。4个圆心角都是90°的扇形,它们的半径不一定相等,不一定可以拼成一个圆形,据此解答。
【详解】由分析可知:用4个圆心角都是90°且半径相等的扇形,一定可以拼成一个圆。题目中未说明4个扇形半径是否相等,因此不一定能拼成一个圆。
故答案为:×
【点睛】扇形的大小不仅与圆心角有关,也与扇形的半径有关。
13.×
【分析】扇形的面积=πr2×,据此分析。
【详解】扇形的面积除了与圆心角的大小有关,还与半径的长短有关系,所以原题说法错误。
故答案为:×
【点睛】关键是掌握并灵活运用扇形面积公式。
14.√
【分析】根据弧长=2πr×,可知弧长不仅与半径长度有关,还与它所对的圆心角的度数大小有关。一个因数不变,另一个因数扩大到原来的几倍或缩小到原来的几分之一(0除外),积也扩大到原来几倍或缩小到原来的几分之一;据此解答。
【详解】根据分析可知,一个扇形的圆心角不变,半径越大,弧就越长。此说法正确。
故答案为:√
【点睛】此题考查了弧长公式的灵活应用。
15.12.56;10.99
【分析】圆环的面积=,其中R指的是外圆的半径,r指的是内圆的半径,第一个扇环占整个圆环的,所以用圆环的面积乘,就是第一个扇环的面积;第二个扇环相当于圆环的面积,所以用圆环的面积乘就是这个扇环的面积。
【详解】(1)5-2=3(dm)
=
=50.24()
(2)4-1=3(dm)
=
=10.99()
16.13.76平方厘米
【分析】观察题意可知,空白部分的面积相当于一个直径是8厘米的圆面积,阴影部分的面积等于一个边长为8厘米的正方形面积减去空白部分的面积,根据正方形的面积公式和圆面积公式,代入数据分别求出正方形的面积和空白部分的面积,最后求出它们的差即可。
【详解】8÷2=4(厘米)
8×8-3.14×42
=8×8-3.14×16
=64-50.24
=13.76(平方厘米)
阴影部分的面积是13.76平方厘米。
17.(1)见详解;(2)28.26;(3)见详解
【分析】(1)根据题意,画出的圆的直径是6米。在长方形内找出一个合适的点作为圆心,取半径3米,画出这个圆;
(2)圆面积=3.14×半径2,据此列式求出这个圆的面积;
(3)以圆心为顶点,利用量角器画出一个105度的角,延长角的两边和圆周相交,画出扇形。
【详解】
(2)6÷2=3(米)
3.14×32=28.26(平方米)
所以,这个圆形花坛的面积为28.26平方米。
(1)(3)如图:
【点睛】本题考查了画圆及扇形、圆的面积,掌握圆和扇形的作图方法、圆的面积公式是解题的关键。
18.4.14平方厘米
【分析】根据题干可得:中间边长为1厘米的正方形,四周连接的圆心角90°扇形的半径也为1厘米,这四个圆心角为90°的扇形可拼接为一个半径1厘米的圆,根据圆面积=πr2,再加上正方形面积=边长×边长,可得出答案。
【详解】图形面积为:
(平方厘米)
答:整个图形的面积是4.14平方厘米。
【点睛】本题主要考查的是圆面积及正方形面积的应用,解题的关键是理解图形四周的圆心角90°扇形可以拼接成一个圆,进而计算得出答案。
19.58.875平方米;23.55米
【分析】由图可知,羊圈的面积占整个圆面积的,需要栅栏的长度占整个圆周长的,利用“”“”分别求出羊圈的面积和需要栅栏的长度,据此解答。
【详解】3.14×(10÷2)2×
=3.14×25×
=78.5×0.75
=58.875(平方米)
3.14×10×
=31.4×0.75
=23.55(米)
答:围成的羊圈面积是58.875平方米,至少需要23.55米长的栅栏。
【点睛】本题主要考查圆的周长和面积公式的应用,熟记公式是解答题目的关键。
答案第1页,共2页
答案第1页,共2页
