新人教A版必修第二册高中数学第九章 统计 单元素养测评卷(含解析)
文档属性
| 名称 | 新人教A版必修第二册高中数学第九章 统计 单元素养测评卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 394.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-13 00:00:00 | ||
图片预览



文档简介
单元素养测评卷(九) 统计
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某学校为了解高一1 200名新入学学生的数学成绩,从中抽取了100名学生进行调查分析,在这个问题中,被抽取的100名学生的数学成绩是( )
A.总体 B.样本 C.个体 D.样本量
2.现有以下两项调查:①从100台刚出厂的电视机中抽取3台进行质量检查;②某社区有1 000户家庭,其中高收入家庭100户,中等收入家庭820户,低收入家庭80户,为了调查家庭每年生活费的开支情况,计划抽取一个容量为50的样本,则完成这两项调查最适宜采用的抽样方法分别是( )
A.①②都采用简单随机抽样 B.①②都采用分层随机抽样
C.①采用简单随机抽样,②采用分层随机抽样 D.①采用分层随机抽样,②采用简单随机抽样
3.[2023·广东中山高一期末]数据1,2,3,4,5,6,7,8,9的80%分位数为( )
A.7 B.7.2 C.7.5 D.8
4.[2023·河南洛阳高一期末]一家水果店的老板为了解本店苹果的日销售情况,记录了过去10天苹果的日销售量(单位:kg):83,96,107,91,74,75,94,80,80,100.设该水果店过去10天苹果日销售量的平均数、中位数、极差依次为a,b,c,则a-b+c的值为( )
A.32 B.33 C.34 D.35
5.[2023·山东烟台高一期末]白鹤是国家一级重点保护鸟类.我国境内的白鹤每年在鄱阳湖的越冬地与西伯利亚的繁殖地之间迁徙,莫莫格湿地是其迁徙途中重要的停歇地.2022年春季,某研究小组为统计莫莫格湿地停歇的白鹤数量,从该湿地随机选取了200只白鹤并做上标记后放回,一段时间后又从该湿地随机选取了200只白鹤,其中有12只白鹤具有标记,据此估计该湿地内白鹤的数量大致为( )
A.2 500 B.3 300 C.4 000 D.4 300
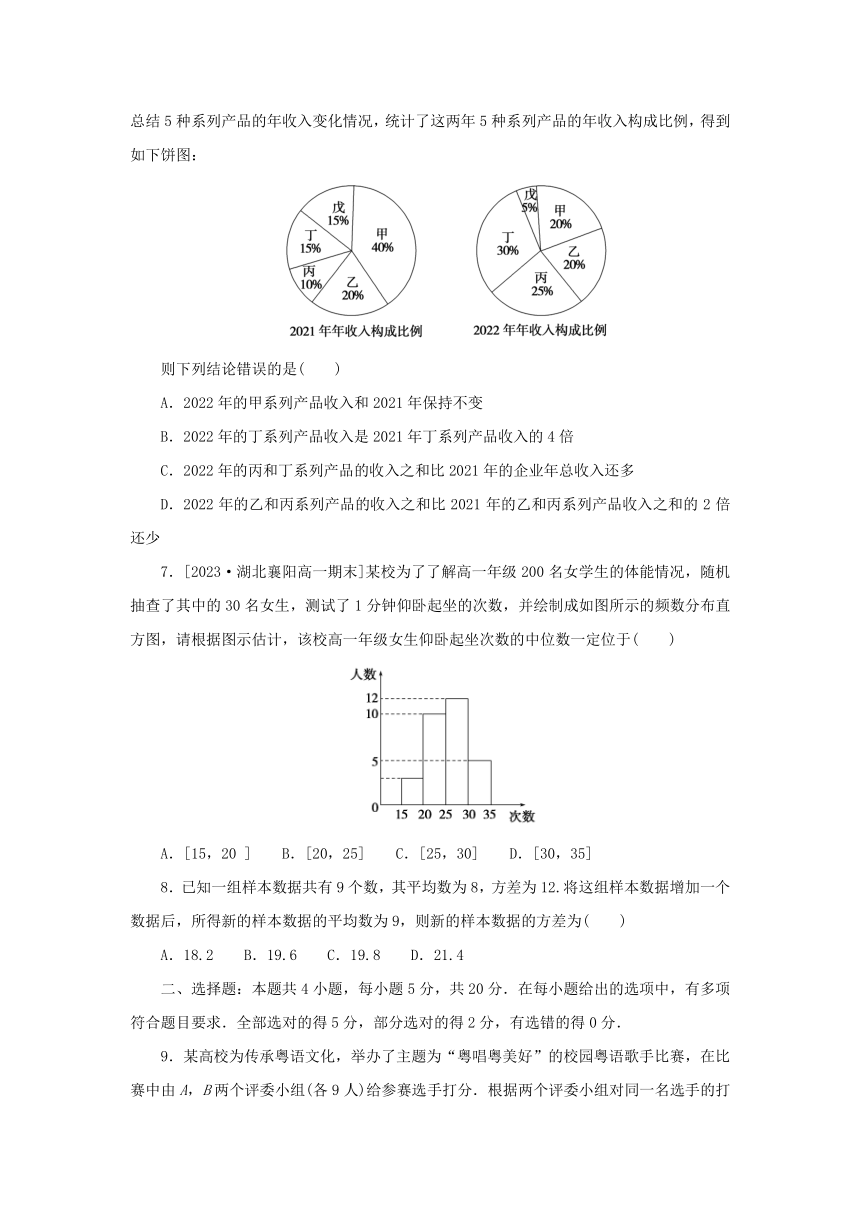
6.某企业为响应国家新旧动能转换的号召,积极调整企业拥有的5种系列产品的结构比例,并坚持自主创新提升产业技术水平,2022年年总收入是2021年的2倍,为了更好的总结5种系列产品的年收入变化情况,统计了这两年5种系列产品的年收入构成比例,得到如下饼图:
则下列结论错误的是( )
A.2022年的甲系列产品收入和2021年保持不变
B.2022年的丁系列产品收入是2021年丁系列产品收入的4倍
C.2022年的丙和丁系列产品的收入之和比2021年的企业年总收入还多
D.2022年的乙和丙系列产品的收入之和比2021年的乙和丙系列产品收入之和的2倍还少
7.[2023·湖北襄阳高一期末]某校为了了解高一年级200名女学生的体能情况,随机抽查了其中的30名女生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示估计,该校高一年级女生仰卧起坐次数的中位数一定位于( )
A.[15,20 ] B.[20,25] C.[25,30] D.[30,35]
8.已知一组样本数据共有9个数,其平均数为8,方差为12.将这组样本数据增加一个数据后,所得新的样本数据的平均数为9,则新的样本数据的方差为( )
A.18.2 B.19.6 C.19.8 D.21.4
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
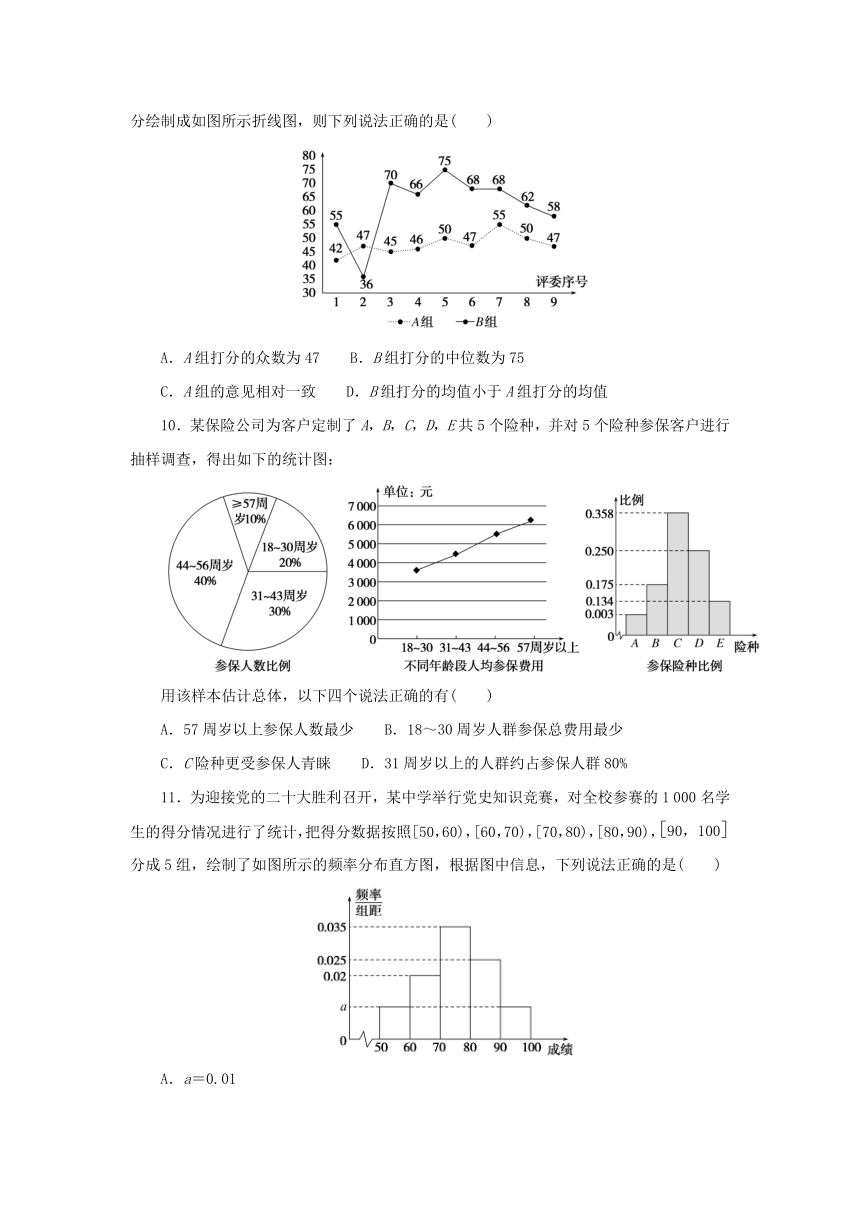
9.某高校为传承粤语文化,举办了主题为“粤唱粤美好”的校园粤语歌手比赛,在比赛中由A,B两个评委小组(各9人)给参赛选手打分.根据两个评委小组对同一名选手的打分绘制成如图所示折线图,则下列说法正确的是( )
A.A组打分的众数为47 B.B组打分的中位数为75
C.A组的意见相对一致 D.B组打分的均值小于A组打分的均值
10.某保险公司为客户定制了A,B,C,D,E共5个险种,并对5个险种参保客户进行抽样调查,得出如下的统计图:
用该样本估计总体,以下四个说法正确的有( )
A.57周岁以上参保人数最少 B.18~30周岁人群参保总费用最少
C.C险种更受参保人青睐 D.31周岁以上的人群约占参保人群80%
11.为迎接党的二十大胜利召开,某中学举行党史知识竞赛,对全校参赛的1 000名学生的得分情况进行了统计,把得分数据按照[50,60),[60,70),[70,80),[80,90),分成5组,绘制了如图所示的频率分布直方图,根据图中信息,下列说法正确的是( )
A.a=0.01
B.得分在区间[60,70)内的学生人数为200
C.该校学生党史知识竞赛成绩的中位数大于80
D.估计该校学生党史知识竞赛成绩的平均数落在区间[70,80)内
12.在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数≤3 B.平均数≤3且标准差s≤2
C.平均数≤3且极差小于或等于2 D.众数等于1且极差小于或等于4
三、填空题:本题共4小题,每小题5分,共20分.
13.在考察某中学的学生身高时,采用分层抽样的方法抽取男生24人,女生16人,得到了男生的平均身高是170 cm,女生的平均身高是165 cm,则估计该校全体学生的平均身高是________cm.
14.已知一组样本数据x1,x2,…,x10,且x+x+…+x=2 020, 平均数=11,则该组数据的标准差为________.
15.如图所示是一个样本容量为100的频率分布直方图,则由图形中的数据,可知其40%分位数为________.
16.已知样本的各个个体的值由小到大依次为2,3,3,7,a,b,12,13,19,20(a,b∈N),且样本的中位数为10.5,则a+b=________;若要使该样本的方差最小,则ab=________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)某大型企业针对改善员工福利的A,B,C三种方案进行了问卷调查,调查结果如下:
支持A方案 支持B方案 支持C方案
35岁以下的人数 200 400 800
35岁及以上的人数 100 100 400
(1)从所有参与调查的人中,用分层随机抽样的方法抽取n人,已知从支持A方案的人中抽取了6人,求n的值.
(2)从支持B方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
18.(12分)某校举行演讲比赛,10位评委对一名选手的评分数据如下:
8.0 7.7 8.1 8.2 7.6 7.8 7.9 8.7 8.8 7.5
(1)根据以上数据,估计该选手得分的样本数据的第75百分位数;
(2)该选手的最终得分为去掉一个最低分和一个最高分,求剩下8个评分数据的平均数和方差.
19.(12分)“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的2.8%,全世界近80%人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨):一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由.
20.(12分)某中学数学组积极研讨网上教学策略,决定先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级进行了7次测试,成绩统计结果如图所示.
(1)请填写下表(要求写出计算过程):
平均数 方差
甲
乙
(2)从下列三个不同的角度对这次方案选择的结果进行分析:
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).
21.
(12分)“天宫课堂”是为发挥中国空间站的综合效益,推出的首个太空科普教育品牌.“天宫课堂”是结合载人飞行任务,贯穿中国空间站建造和在轨运营系列化推出的,将由中国航天员担任“太空教师”,以青少年为主要对象,采取天地协同互动方式开展.2022年10月12日15时40分,“天宫课堂”第三课在中国空间站开讲.学校针对这次直播课,举办了“天宫课堂”知识竞赛,有100名学生代表参加了竞赛,竞赛后对这100名学生的成绩(满分100分)进行统计,将数据分为[60,70),[70,80),[80,90),[90,100]这4组,画出如图所示的频率分布直方图.
(1)求频率分布直方图中m的值;
(2)估计这100名学生竞赛成绩的平均数(同一组中的数据用该组区间的中点值作为代表);
(3)若该校准备对本次知识竞赛成绩较好的40%的学生进行嘉奖,试问被嘉奖的学生的分数不低于多少?
22.
(12分)[2023·山东济南高一期末]为了调查某中学高一年级学生的身高情况,在高一年级随机抽取100名学生作为样本,把他们的身高(单位:cm)按照区间[160,165),[165,170),[170,175),[175,180),分组,得到样本身高的频率分布直方图如图所示.
(1)求频率分布直方图中x的值以及样本中身高不低于175 cm的学生人数;
(2)在统计过程中,小明与小张两位同学因事缺席,测得其余98名同学的平均身高为172 cm,方差为29.之后补测得到小明与小张的身高分别为171 cm与173 cm.试根据上述数据求样本的方差.
单元素养测评卷(九) 统计
1.答案:B
解析:根据定义,被抽取的100名学生的数学成绩是样本.故选B.
2.答案:C
解析:①的总体中的个体数较少,宜采用简单随机抽样,
②中1000户家庭中层次比较明显,宜采用分层抽样.
故选C.
3.答案:D
解析:因为9×80%=7.2,所以第80%分位数为第8个数,
故数据1,2,3,4,5,6,7,8,9的第80百分位数为8.故选D.
4.答案:C
解析:由题设,从小到大排序为74,75,80,80,83,91,94,96,100,107,
所以平均数为
a==88,
中位数为b==87,
极差为c=107-74=33,
所以a-b+c=88-87+33=34.故选C.
5.答案:B
解析:设该湿地有白鹤x只,由题意,= x≈3333.故选B.
6.答案:D
解析:设2021年年总收入为W,则2022年年总收入为2W,观察饼图,
对于A,2021年的甲系列产品收入为0.4W,2022年的甲系列产品收入为2W×20%=0.4W,A正确;
对于B,2021年丁系列产品收入为0.15W,2022年的丁系列产品收入为2W×30%=0.6W,0.6W=4×0.15W,B正确;
对于C,2022年的丙和丁系列产品的收入之和为2W×(30%+25%)=1.1W>W,C正确;
对于D,2021年的乙和丙系列产品收入之和为(10%+20%)W=0.3W,2022年的乙和丙系列产品的收入之和为2W×(20%+25%)=0.9W,显然0.9W>2×0.3W,D不正确.故选D.
7.答案:C
解析:由题意知:区间的人数有30-10-12-5=3人,又3+10<15,3+10+12>16,故中位数位于.故选C.
8.答案:C
解析:设增加的数为k,原来的9个数分别为a1,a2,…,a9,
则a1+a2+…+a9=72,a1+a2+…+a9+k=90,
所以k=18,
又因为2=12,即2=108,
所以[2+(k-9)2]
=[2-2+9+81]=19.8.故选C.
9.答案:AC
解析:由折线图可知,小组A打分的分值为:42,47,45,46,50,47,50,47,
则小组A打分的分值的众数为47,故选项A正确;
小组B打分的分值为:55,36,70,66,75,68,68,62,58,
按照从小到大排列为:36,55,58,62,66,68,68,70,75,
中间数为66,故中位数为66,故选项B错误;
小组A的打分成绩比较均匀,波动更小,故A小组意见相对一致,故选项C正确;
小组A的打分分值的均值=46.7,而小组B的打分分值的均值
=62,
所以小组B打分的分值的均值大于小组A打分的分值的均值,故选项D错误.故选AC.
10.答案:ACD
解析:由扇形图可知,57周岁以上参保人数最少,故A正确;
由折线图可知,18~30周岁人群人均参保费用最少,但是由扇形图知参保人数并不是最少的,所以参保总费用不是最少,故B错误;
由条形图可知,C险种参保比例最高,故C正确;
由扇形图可知,31周岁以上的人群约占参保人群80%,故D正确.故选ACD.
11.答案:ABD
解析:对于A,由频率分布直方图性质得:(a+0.02+0.035+0.025+a)×10=1,解得a=0.01,故A正确;
对于B,由频率分布直方图得:成绩落在区间的频率为0.2,所以人数为0.2×1000=200,故B正确;
对于C,由频率分布直方图得:的频率为×10=0.3,的频率为0.035×10=0.35,所以成绩的中位数位于区间内,故C错误;
对于D,估计成绩的平均数为:=55×0.01×10+65×0.02×10+75×0.035×10+85×0.025×10+95×0.01×10=75.5,所以成绩的平均数落在区间内,故D正确.故选ABD.
12.答案:CD
解析:A错,举反例:0,0,0,0,2,6,6,其平均数=2≤3,不符合指标;
B错,举反例:0,3,3,3,3,3,6,其平均数=3,且标准差s=≤2,不符合指标;
C对,若极差等于0或1,在≤3的条件下,显然符合指标;若极差等于2且≤3,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标;D对,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.故选CD.
13.答案:168
解析:估计该校全体学生的平均身高为=168cm.
14.答案:9
解析:根据题意,一组样本数据x1,x2,…,x10,且x+x+…+x=2020,
平均数=11,
则其方差s2=[2+2+…+2]
==(2020-10×112)=81,
则其标准差s==9.
15.答案:12
解析:由图可知第一组的频率为0.04×5=0.2<0.4,
前两组的频率之和为0.04×5+0.1×5=0.7>0.4,
则可知其40%分位数在内,设为x,
则0.1×=0.4-0.2,解得x=12.
16.答案:21 110
解析:因为样本的各个个体的值由小到大依次为2,3,3,7,a,b,12,13,19,20,且样本的中位数为10.5,
所以=10.5,即a+b=21;
所以样本平均数为=10.
要使样本方差最小,即(a-10)2+(b-10)2最小,
又因为(a-10)2+(b-10)2=(21-b-10)2+(b-10)2=(11-b)2+(b-10)2=2b2-42b+221=2(b-)2+,
a,b∈N,
所以当b=11或b=10时,(a-10)2+(b-10)2取得最小值,
又a+b=21,
所以a=11,b=10或a=10,b=11,
所以ab=110.
17.解析:(1)由题意得
=,解得n=40.
(2)年龄在35岁以下的人数为×400=4,
年龄在35岁及以上的人数为×100=1.
18.解析:(1)将数据进行排序得到7.5,7.6,7.7,7.8,7.9,8.0,8.1,8.2,8.7,8.8.
因为样本数据的第75百分位数,
所以10×75%=7.5,
该选手评分的样本数据为第八个数据,
所以该选手评分的样本数据的第75百分位数为8.2.
(2)去掉一个最低分7.5和一个最高分8.8,
剩下8个评分数据的平均数为:
=8,
所以其方差为:
[(7.6-8)2+(7.7-8)2+(7.8-8)2+(7.9-8)2+(8.0-8)2+(8.1-8)2+(8.2-8)2+(8.7-8)2]=0.055.
19.解析:(1)由概率统计相关知识,可知各组频率之和的值为1,
即频率分布直方图各小矩形面积之和为1,
∴0.5×(0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a)=1,解得a=0.3.
(2)由图可知,不低于2.5吨人数所占百分比为0.5×=27%,
∴全市月均用水量不低于2.5吨的人数为:60×0.27=16.2(万).
20.解析:(1)由折线图中的数据可得甲方案测试成绩的平均分为甲==115,
方差为s==16,
乙方案测试成绩的平均分为
乙==115,
方差为s==.
填表如下:
平均数 方差
甲 115 16
乙 115
(2)①甲、乙两种方案的平均数相等,且s>s,
故乙方案的成绩更稳定,故乙方案的成绩更好;
②从折线图的走势上看甲方案更有潜力,
因为使用甲方案成绩稳步提高,而使用乙方案成绩不稳定,忽高忽低.
21.解析:(1)由图可得(m+5m+0.03+0.04)×10=1,解得m=0.005.
(2)估计这100名学生竞赛成绩的平均数=65×0.005×10+75×0.025×10+85×0.04×10+95×0.03×10=84.5.
(3)设被嘉奖的学生的分数不低于x,
因为第四组的频率为0.03×10=0.3,第三组的频率为0.04×10=0.4,
所以x∈,所以0.04×+0.3=0.4,得x=87.5.
22.解析:(1)由频率分布直方图知,(0.01+0.02+x+0.06+0.07)×5=1,所以x=0.04.
又样本中身高不低于175cm的学生的频率为×5=0.3,
所以,样本中身高不低于175cm的学生人数为100×0.3=30人.
(2)设除小张与小明外其他98名同学的身高为x1,x2,x3,…,x98,小张与小明的身高分别为x99,x100,样本的平均数为,样本的方差为s2.
由题意===172cm.
又2+2+…+2=98×29=2842,
所以样本的方差s2=2
==28.44.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某学校为了解高一1 200名新入学学生的数学成绩,从中抽取了100名学生进行调查分析,在这个问题中,被抽取的100名学生的数学成绩是( )
A.总体 B.样本 C.个体 D.样本量
2.现有以下两项调查:①从100台刚出厂的电视机中抽取3台进行质量检查;②某社区有1 000户家庭,其中高收入家庭100户,中等收入家庭820户,低收入家庭80户,为了调查家庭每年生活费的开支情况,计划抽取一个容量为50的样本,则完成这两项调查最适宜采用的抽样方法分别是( )
A.①②都采用简单随机抽样 B.①②都采用分层随机抽样
C.①采用简单随机抽样,②采用分层随机抽样 D.①采用分层随机抽样,②采用简单随机抽样
3.[2023·广东中山高一期末]数据1,2,3,4,5,6,7,8,9的80%分位数为( )
A.7 B.7.2 C.7.5 D.8
4.[2023·河南洛阳高一期末]一家水果店的老板为了解本店苹果的日销售情况,记录了过去10天苹果的日销售量(单位:kg):83,96,107,91,74,75,94,80,80,100.设该水果店过去10天苹果日销售量的平均数、中位数、极差依次为a,b,c,则a-b+c的值为( )
A.32 B.33 C.34 D.35
5.[2023·山东烟台高一期末]白鹤是国家一级重点保护鸟类.我国境内的白鹤每年在鄱阳湖的越冬地与西伯利亚的繁殖地之间迁徙,莫莫格湿地是其迁徙途中重要的停歇地.2022年春季,某研究小组为统计莫莫格湿地停歇的白鹤数量,从该湿地随机选取了200只白鹤并做上标记后放回,一段时间后又从该湿地随机选取了200只白鹤,其中有12只白鹤具有标记,据此估计该湿地内白鹤的数量大致为( )
A.2 500 B.3 300 C.4 000 D.4 300
6.某企业为响应国家新旧动能转换的号召,积极调整企业拥有的5种系列产品的结构比例,并坚持自主创新提升产业技术水平,2022年年总收入是2021年的2倍,为了更好的总结5种系列产品的年收入变化情况,统计了这两年5种系列产品的年收入构成比例,得到如下饼图:
则下列结论错误的是( )
A.2022年的甲系列产品收入和2021年保持不变
B.2022年的丁系列产品收入是2021年丁系列产品收入的4倍
C.2022年的丙和丁系列产品的收入之和比2021年的企业年总收入还多
D.2022年的乙和丙系列产品的收入之和比2021年的乙和丙系列产品收入之和的2倍还少
7.[2023·湖北襄阳高一期末]某校为了了解高一年级200名女学生的体能情况,随机抽查了其中的30名女生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示估计,该校高一年级女生仰卧起坐次数的中位数一定位于( )
A.[15,20 ] B.[20,25] C.[25,30] D.[30,35]
8.已知一组样本数据共有9个数,其平均数为8,方差为12.将这组样本数据增加一个数据后,所得新的样本数据的平均数为9,则新的样本数据的方差为( )
A.18.2 B.19.6 C.19.8 D.21.4
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.某高校为传承粤语文化,举办了主题为“粤唱粤美好”的校园粤语歌手比赛,在比赛中由A,B两个评委小组(各9人)给参赛选手打分.根据两个评委小组对同一名选手的打分绘制成如图所示折线图,则下列说法正确的是( )
A.A组打分的众数为47 B.B组打分的中位数为75
C.A组的意见相对一致 D.B组打分的均值小于A组打分的均值
10.某保险公司为客户定制了A,B,C,D,E共5个险种,并对5个险种参保客户进行抽样调查,得出如下的统计图:
用该样本估计总体,以下四个说法正确的有( )
A.57周岁以上参保人数最少 B.18~30周岁人群参保总费用最少
C.C险种更受参保人青睐 D.31周岁以上的人群约占参保人群80%
11.为迎接党的二十大胜利召开,某中学举行党史知识竞赛,对全校参赛的1 000名学生的得分情况进行了统计,把得分数据按照[50,60),[60,70),[70,80),[80,90),分成5组,绘制了如图所示的频率分布直方图,根据图中信息,下列说法正确的是( )
A.a=0.01
B.得分在区间[60,70)内的学生人数为200
C.该校学生党史知识竞赛成绩的中位数大于80
D.估计该校学生党史知识竞赛成绩的平均数落在区间[70,80)内
12.在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
A.平均数≤3 B.平均数≤3且标准差s≤2
C.平均数≤3且极差小于或等于2 D.众数等于1且极差小于或等于4
三、填空题:本题共4小题,每小题5分,共20分.
13.在考察某中学的学生身高时,采用分层抽样的方法抽取男生24人,女生16人,得到了男生的平均身高是170 cm,女生的平均身高是165 cm,则估计该校全体学生的平均身高是________cm.
14.已知一组样本数据x1,x2,…,x10,且x+x+…+x=2 020, 平均数=11,则该组数据的标准差为________.
15.如图所示是一个样本容量为100的频率分布直方图,则由图形中的数据,可知其40%分位数为________.
16.已知样本的各个个体的值由小到大依次为2,3,3,7,a,b,12,13,19,20(a,b∈N),且样本的中位数为10.5,则a+b=________;若要使该样本的方差最小,则ab=________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)某大型企业针对改善员工福利的A,B,C三种方案进行了问卷调查,调查结果如下:
支持A方案 支持B方案 支持C方案
35岁以下的人数 200 400 800
35岁及以上的人数 100 100 400
(1)从所有参与调查的人中,用分层随机抽样的方法抽取n人,已知从支持A方案的人中抽取了6人,求n的值.
(2)从支持B方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
18.(12分)某校举行演讲比赛,10位评委对一名选手的评分数据如下:
8.0 7.7 8.1 8.2 7.6 7.8 7.9 8.7 8.8 7.5
(1)根据以上数据,估计该选手得分的样本数据的第75百分位数;
(2)该选手的最终得分为去掉一个最低分和一个最高分,求剩下8个评分数据的平均数和方差.
19.(12分)“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的2.8%,全世界近80%人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨):一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由.
20.(12分)某中学数学组积极研讨网上教学策略,决定先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级进行了7次测试,成绩统计结果如图所示.
(1)请填写下表(要求写出计算过程):
平均数 方差
甲
乙
(2)从下列三个不同的角度对这次方案选择的结果进行分析:
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).
21.
(12分)“天宫课堂”是为发挥中国空间站的综合效益,推出的首个太空科普教育品牌.“天宫课堂”是结合载人飞行任务,贯穿中国空间站建造和在轨运营系列化推出的,将由中国航天员担任“太空教师”,以青少年为主要对象,采取天地协同互动方式开展.2022年10月12日15时40分,“天宫课堂”第三课在中国空间站开讲.学校针对这次直播课,举办了“天宫课堂”知识竞赛,有100名学生代表参加了竞赛,竞赛后对这100名学生的成绩(满分100分)进行统计,将数据分为[60,70),[70,80),[80,90),[90,100]这4组,画出如图所示的频率分布直方图.
(1)求频率分布直方图中m的值;
(2)估计这100名学生竞赛成绩的平均数(同一组中的数据用该组区间的中点值作为代表);
(3)若该校准备对本次知识竞赛成绩较好的40%的学生进行嘉奖,试问被嘉奖的学生的分数不低于多少?
22.
(12分)[2023·山东济南高一期末]为了调查某中学高一年级学生的身高情况,在高一年级随机抽取100名学生作为样本,把他们的身高(单位:cm)按照区间[160,165),[165,170),[170,175),[175,180),分组,得到样本身高的频率分布直方图如图所示.
(1)求频率分布直方图中x的值以及样本中身高不低于175 cm的学生人数;
(2)在统计过程中,小明与小张两位同学因事缺席,测得其余98名同学的平均身高为172 cm,方差为29.之后补测得到小明与小张的身高分别为171 cm与173 cm.试根据上述数据求样本的方差.
单元素养测评卷(九) 统计
1.答案:B
解析:根据定义,被抽取的100名学生的数学成绩是样本.故选B.
2.答案:C
解析:①的总体中的个体数较少,宜采用简单随机抽样,
②中1000户家庭中层次比较明显,宜采用分层抽样.
故选C.
3.答案:D
解析:因为9×80%=7.2,所以第80%分位数为第8个数,
故数据1,2,3,4,5,6,7,8,9的第80百分位数为8.故选D.
4.答案:C
解析:由题设,从小到大排序为74,75,80,80,83,91,94,96,100,107,
所以平均数为
a==88,
中位数为b==87,
极差为c=107-74=33,
所以a-b+c=88-87+33=34.故选C.
5.答案:B
解析:设该湿地有白鹤x只,由题意,= x≈3333.故选B.
6.答案:D
解析:设2021年年总收入为W,则2022年年总收入为2W,观察饼图,
对于A,2021年的甲系列产品收入为0.4W,2022年的甲系列产品收入为2W×20%=0.4W,A正确;
对于B,2021年丁系列产品收入为0.15W,2022年的丁系列产品收入为2W×30%=0.6W,0.6W=4×0.15W,B正确;
对于C,2022年的丙和丁系列产品的收入之和为2W×(30%+25%)=1.1W>W,C正确;
对于D,2021年的乙和丙系列产品收入之和为(10%+20%)W=0.3W,2022年的乙和丙系列产品的收入之和为2W×(20%+25%)=0.9W,显然0.9W>2×0.3W,D不正确.故选D.
7.答案:C
解析:由题意知:区间的人数有30-10-12-5=3人,又3+10<15,3+10+12>16,故中位数位于.故选C.
8.答案:C
解析:设增加的数为k,原来的9个数分别为a1,a2,…,a9,
则a1+a2+…+a9=72,a1+a2+…+a9+k=90,
所以k=18,
又因为2=12,即2=108,
所以[2+(k-9)2]
=[2-2+9+81]=19.8.故选C.
9.答案:AC
解析:由折线图可知,小组A打分的分值为:42,47,45,46,50,47,50,47,
则小组A打分的分值的众数为47,故选项A正确;
小组B打分的分值为:55,36,70,66,75,68,68,62,58,
按照从小到大排列为:36,55,58,62,66,68,68,70,75,
中间数为66,故中位数为66,故选项B错误;
小组A的打分成绩比较均匀,波动更小,故A小组意见相对一致,故选项C正确;
小组A的打分分值的均值=46.7,而小组B的打分分值的均值
=62,
所以小组B打分的分值的均值大于小组A打分的分值的均值,故选项D错误.故选AC.
10.答案:ACD
解析:由扇形图可知,57周岁以上参保人数最少,故A正确;
由折线图可知,18~30周岁人群人均参保费用最少,但是由扇形图知参保人数并不是最少的,所以参保总费用不是最少,故B错误;
由条形图可知,C险种参保比例最高,故C正确;
由扇形图可知,31周岁以上的人群约占参保人群80%,故D正确.故选ACD.
11.答案:ABD
解析:对于A,由频率分布直方图性质得:(a+0.02+0.035+0.025+a)×10=1,解得a=0.01,故A正确;
对于B,由频率分布直方图得:成绩落在区间的频率为0.2,所以人数为0.2×1000=200,故B正确;
对于C,由频率分布直方图得:的频率为×10=0.3,的频率为0.035×10=0.35,所以成绩的中位数位于区间内,故C错误;
对于D,估计成绩的平均数为:=55×0.01×10+65×0.02×10+75×0.035×10+85×0.025×10+95×0.01×10=75.5,所以成绩的平均数落在区间内,故D正确.故选ABD.
12.答案:CD
解析:A错,举反例:0,0,0,0,2,6,6,其平均数=2≤3,不符合指标;
B错,举反例:0,3,3,3,3,3,6,其平均数=3,且标准差s=≤2,不符合指标;
C对,若极差等于0或1,在≤3的条件下,显然符合指标;若极差等于2且≤3,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标;D对,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.故选CD.
13.答案:168
解析:估计该校全体学生的平均身高为=168cm.
14.答案:9
解析:根据题意,一组样本数据x1,x2,…,x10,且x+x+…+x=2020,
平均数=11,
则其方差s2=[2+2+…+2]
==(2020-10×112)=81,
则其标准差s==9.
15.答案:12
解析:由图可知第一组的频率为0.04×5=0.2<0.4,
前两组的频率之和为0.04×5+0.1×5=0.7>0.4,
则可知其40%分位数在内,设为x,
则0.1×=0.4-0.2,解得x=12.
16.答案:21 110
解析:因为样本的各个个体的值由小到大依次为2,3,3,7,a,b,12,13,19,20,且样本的中位数为10.5,
所以=10.5,即a+b=21;
所以样本平均数为=10.
要使样本方差最小,即(a-10)2+(b-10)2最小,
又因为(a-10)2+(b-10)2=(21-b-10)2+(b-10)2=(11-b)2+(b-10)2=2b2-42b+221=2(b-)2+,
a,b∈N,
所以当b=11或b=10时,(a-10)2+(b-10)2取得最小值,
又a+b=21,
所以a=11,b=10或a=10,b=11,
所以ab=110.
17.解析:(1)由题意得
=,解得n=40.
(2)年龄在35岁以下的人数为×400=4,
年龄在35岁及以上的人数为×100=1.
18.解析:(1)将数据进行排序得到7.5,7.6,7.7,7.8,7.9,8.0,8.1,8.2,8.7,8.8.
因为样本数据的第75百分位数,
所以10×75%=7.5,
该选手评分的样本数据为第八个数据,
所以该选手评分的样本数据的第75百分位数为8.2.
(2)去掉一个最低分7.5和一个最高分8.8,
剩下8个评分数据的平均数为:
=8,
所以其方差为:
[(7.6-8)2+(7.7-8)2+(7.8-8)2+(7.9-8)2+(8.0-8)2+(8.1-8)2+(8.2-8)2+(8.7-8)2]=0.055.
19.解析:(1)由概率统计相关知识,可知各组频率之和的值为1,
即频率分布直方图各小矩形面积之和为1,
∴0.5×(0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a)=1,解得a=0.3.
(2)由图可知,不低于2.5吨人数所占百分比为0.5×=27%,
∴全市月均用水量不低于2.5吨的人数为:60×0.27=16.2(万).
20.解析:(1)由折线图中的数据可得甲方案测试成绩的平均分为甲==115,
方差为s==16,
乙方案测试成绩的平均分为
乙==115,
方差为s==.
填表如下:
平均数 方差
甲 115 16
乙 115
(2)①甲、乙两种方案的平均数相等,且s>s,
故乙方案的成绩更稳定,故乙方案的成绩更好;
②从折线图的走势上看甲方案更有潜力,
因为使用甲方案成绩稳步提高,而使用乙方案成绩不稳定,忽高忽低.
21.解析:(1)由图可得(m+5m+0.03+0.04)×10=1,解得m=0.005.
(2)估计这100名学生竞赛成绩的平均数=65×0.005×10+75×0.025×10+85×0.04×10+95×0.03×10=84.5.
(3)设被嘉奖的学生的分数不低于x,
因为第四组的频率为0.03×10=0.3,第三组的频率为0.04×10=0.4,
所以x∈,所以0.04×+0.3=0.4,得x=87.5.
22.解析:(1)由频率分布直方图知,(0.01+0.02+x+0.06+0.07)×5=1,所以x=0.04.
又样本中身高不低于175cm的学生的频率为×5=0.3,
所以,样本中身高不低于175cm的学生人数为100×0.3=30人.
(2)设除小张与小明外其他98名同学的身高为x1,x2,x3,…,x98,小张与小明的身高分别为x99,x100,样本的平均数为,样本的方差为s2.
由题意===172cm.
又2+2+…+2=98×29=2842,
所以样本的方差s2=2
==28.44.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
