2014-2015学年湘教版七年级数学下册课件:4.3 平行线的性质(共15张PPT)
文档属性
| 名称 | 2014-2015学年湘教版七年级数学下册课件:4.3 平行线的性质(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 227.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-29 10:47:12 | ||
图片预览




文档简介
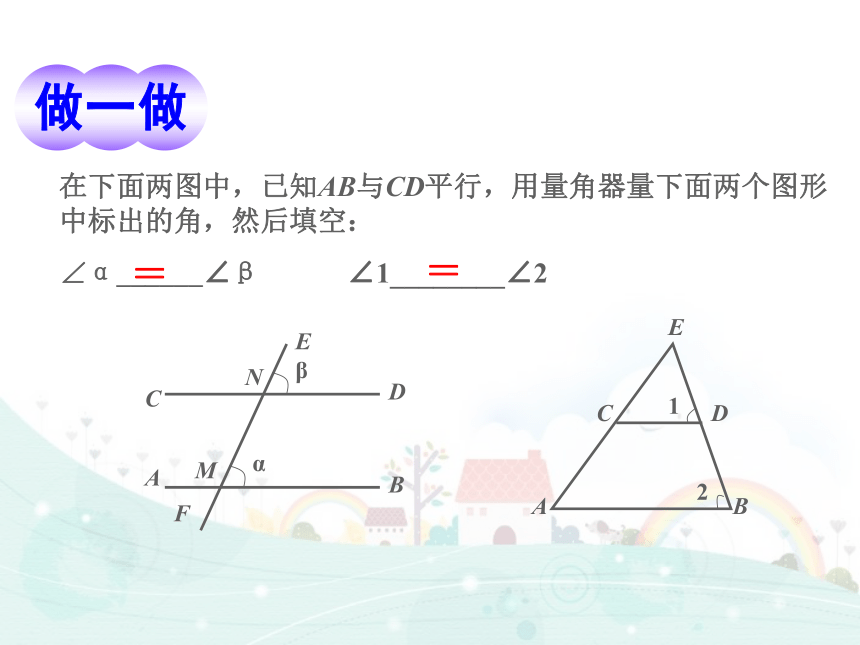
课件15张PPT。4.3 平行线的性质湘教版七年级下册在生产或生活中,我们经常要用到平行线的性质来判断两条直线是否平行,例如铁路护路工人就经常要检查铁轨是否平行.在下面两图中,已知AB与CD平行,用量角器量下面两个图形中标出的角,然后填空:
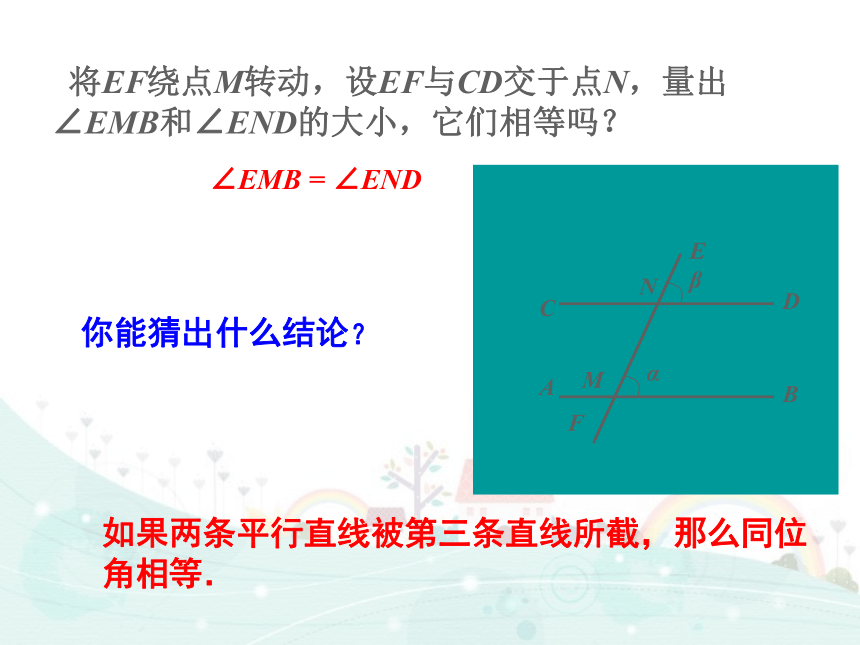
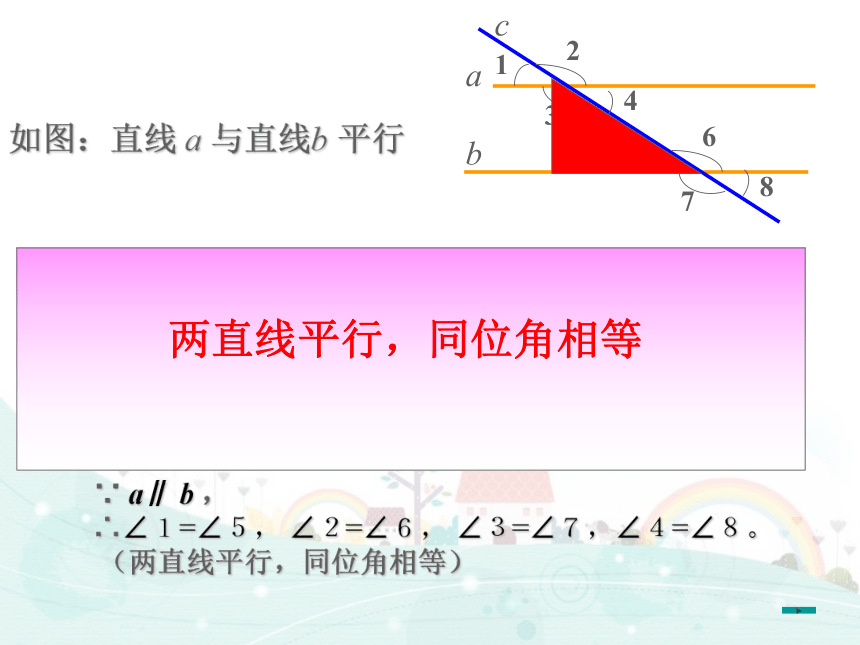
∠α______∠β ∠1________∠2ABCDE12==ABCDENMFαβ 将EF绕点M转动,设EF与CD交于点N,量出∠EMB和∠END的大小,它们相等吗?你能猜出什么结论?ABCDENMFαβ如果两条平行直线被第三条直线所截,那么同位角相等.∠EMB = ∠END作平移使∠α的顶点M移到∠β的顶点N处,由于平移把直线AB变成与它平行的直线,又已知AB//CD,且CD经过点N,因此上述平移把直线AB变成直线CD,从而∠ α变成∠ β ,所以∠ α =∠β.ABCDENMFαβ根据以上操作,我们猜想:如果两条平行直线被第三条直线所截,那么同位角相等.这个猜想对吗?如图,设AB//CD,截线EF与AB,CD分别相交于M,N两点.如图:直线 a 与直线b 平行两直线平行,同位角相等∵ a∥ b ,
∴∠1=∠5, ∠2=∠6, ∠3=∠7,∠4=∠8。
(两直线平行,同位角相等) 两直线平行,内错角有什么关系呢? 两直线平行,内错角相等 ∵a∥b,
∴∠1=∠5。(两直线平行,同位角相等)又∵∠1=∠4,
∴∠4= ∠ 5。两直线平行,同旁内角有什么关系呢?
∴∠5+ ∠3=180°。两直线平行,同旁内角互补 ∵a∥b,
∴∠1=∠5。(两直线平行,同位角相等)又∵∠1+ ∠3=180°,
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.简单说成:性质Ⅰ 两条平行线被第三条直线所截,
同位角相等.性质II 两条平行线被第三条直线所截,内错角相等.
性质III 两条平行线被第三条直线所截,同旁内角互补.如图,已知AB//CD,∠1=105o
∠1与∠2是______角,因此∠2_______ ∠1=_______;
∠1与∠4是______ 角,因此∠4_______ ∠1=_______;
∠1与∠3是______ 角,
因此∠3=______________ =_______.内错=105o同位=105o同旁内180-105o75o如图,在A,B两地之间要修建一条公路,在A地测得公路的走向是北偏东80o,即∠α=80o,现在要求在A,B两地同时施工,那么在B地公路走向应按∠β等于多少度施工? 因为AC,BD方向相同,所以AC//BD, 因为∠α与∠β是同旁内角,所以∠α+∠β=180o,从而∠β=180o-∠α=180o-80o=100o答:在B地应按∠β=100o的方向施工.解1.如图,a//b,∠1=60o,求∠2的度数.因为 a∥b∴所以∠1=∠3(同位角相等)又 ∠2+∠3=180°∴ 所以∠2=180°-∠3=180°-60°=120°解32.如图,AB//CD,CD//EF,BC//DE,已知∠B=70o,求∠C, ∠D和∠E的度数.因为AB∥CD所以∠C=∠B=70°又BC∥DE∠C+∠D=180°所以 ∠D=180°-∠C=180°-70°=110°又CD∥EF所以∠D=∠E所以∠E=∠D=110°.解A3. 已知∠C=∠AED,BE平分∠ABC,
试说明: ∠DBE=∠DEB.1234解
∵ ∠C=∠ 1 ∴BC∥DE(同位角相等,两直线平行)∴∠2=∠3 (两直线平行,内错角角相等) ∵BE平分∠ABC∴∠3=∠4 ∴∠2=∠4 再 见
∠α______∠β ∠1________∠2ABCDE12==ABCDENMFαβ 将EF绕点M转动,设EF与CD交于点N,量出∠EMB和∠END的大小,它们相等吗?你能猜出什么结论?ABCDENMFαβ如果两条平行直线被第三条直线所截,那么同位角相等.∠EMB = ∠END作平移使∠α的顶点M移到∠β的顶点N处,由于平移把直线AB变成与它平行的直线,又已知AB//CD,且CD经过点N,因此上述平移把直线AB变成直线CD,从而∠ α变成∠ β ,所以∠ α =∠β.ABCDENMFαβ根据以上操作,我们猜想:如果两条平行直线被第三条直线所截,那么同位角相等.这个猜想对吗?如图,设AB//CD,截线EF与AB,CD分别相交于M,N两点.如图:直线 a 与直线b 平行两直线平行,同位角相等∵ a∥ b ,
∴∠1=∠5, ∠2=∠6, ∠3=∠7,∠4=∠8。
(两直线平行,同位角相等) 两直线平行,内错角有什么关系呢? 两直线平行,内错角相等 ∵a∥b,
∴∠1=∠5。(两直线平行,同位角相等)又∵∠1=∠4,
∴∠4= ∠ 5。两直线平行,同旁内角有什么关系呢?
∴∠5+ ∠3=180°。两直线平行,同旁内角互补 ∵a∥b,
∴∠1=∠5。(两直线平行,同位角相等)又∵∠1+ ∠3=180°,
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.简单说成:性质Ⅰ 两条平行线被第三条直线所截,
同位角相等.性质II 两条平行线被第三条直线所截,内错角相等.
性质III 两条平行线被第三条直线所截,同旁内角互补.如图,已知AB//CD,∠1=105o
∠1与∠2是______角,因此∠2_______ ∠1=_______;
∠1与∠4是______ 角,因此∠4_______ ∠1=_______;
∠1与∠3是______ 角,
因此∠3=______________ =_______.内错=105o同位=105o同旁内180-105o75o如图,在A,B两地之间要修建一条公路,在A地测得公路的走向是北偏东80o,即∠α=80o,现在要求在A,B两地同时施工,那么在B地公路走向应按∠β等于多少度施工? 因为AC,BD方向相同,所以AC//BD, 因为∠α与∠β是同旁内角,所以∠α+∠β=180o,从而∠β=180o-∠α=180o-80o=100o答:在B地应按∠β=100o的方向施工.解1.如图,a//b,∠1=60o,求∠2的度数.因为 a∥b∴所以∠1=∠3(同位角相等)又 ∠2+∠3=180°∴ 所以∠2=180°-∠3=180°-60°=120°解32.如图,AB//CD,CD//EF,BC//DE,已知∠B=70o,求∠C, ∠D和∠E的度数.因为AB∥CD所以∠C=∠B=70°又BC∥DE∠C+∠D=180°所以 ∠D=180°-∠C=180°-70°=110°又CD∥EF所以∠D=∠E所以∠E=∠D=110°.解A3. 已知∠C=∠AED,BE平分∠ABC,
试说明: ∠DBE=∠DEB.1234解
∵ ∠C=∠ 1 ∴BC∥DE(同位角相等,两直线平行)∴∠2=∠3 (两直线平行,内错角角相等) ∵BE平分∠ABC∴∠3=∠4 ∴∠2=∠4 再 见
