【新学期备课参考】2014-2015学年华师大版七年级数学下册:9.2 多边形的内角和与外角和课件
文档属性
| 名称 | 【新学期备课参考】2014-2015学年华师大版七年级数学下册:9.2 多边形的内角和与外角和课件 |  | |
| 格式 | zip | ||
| 文件大小 | 914.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-29 11:40:26 | ||
图片预览



文档简介
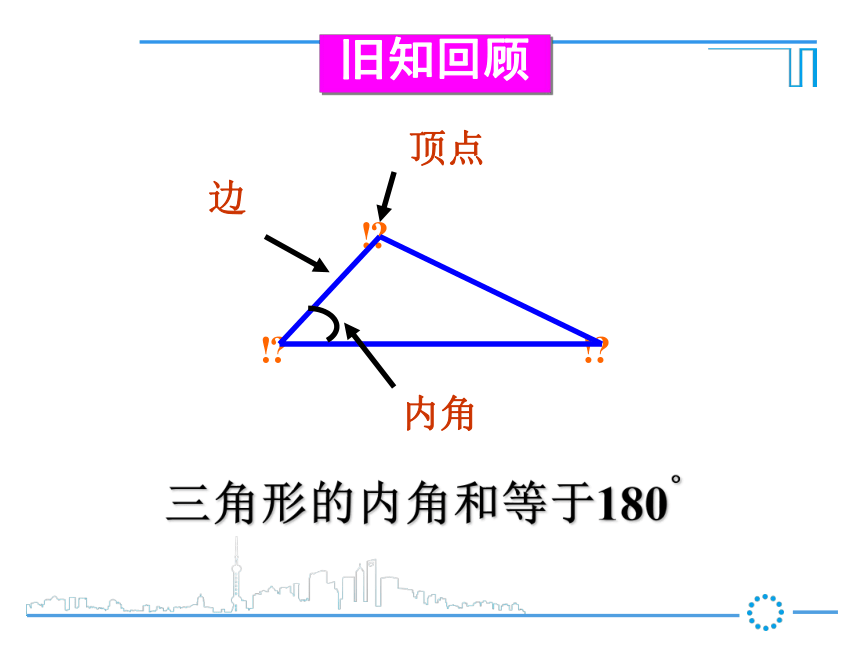
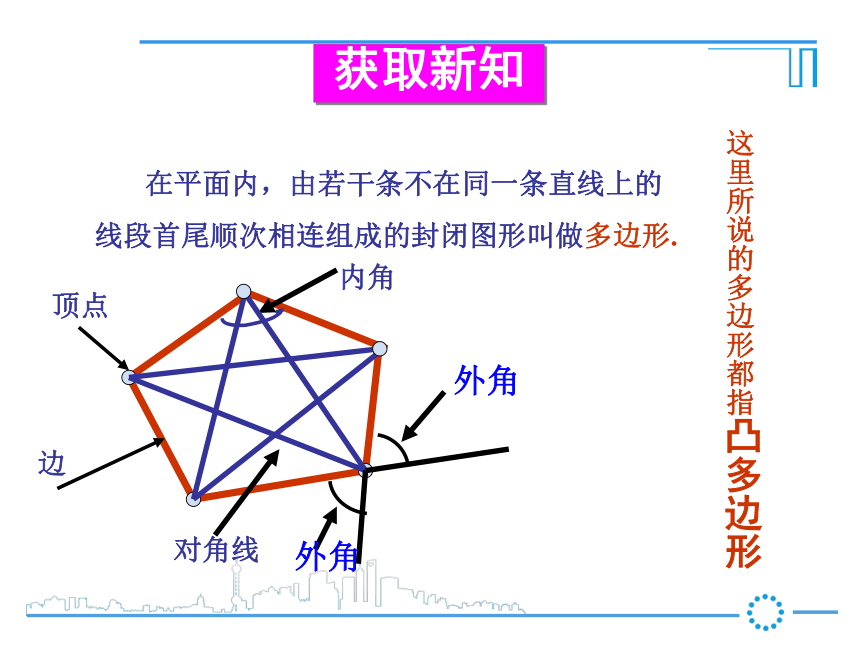
课件21张PPT。华东师大·七年级下册9.2 多边形的内角和与外角和???顶点边内角旧知回顾三角形的内角和等于180° 在平面内,由若干条不在同一条直线上的
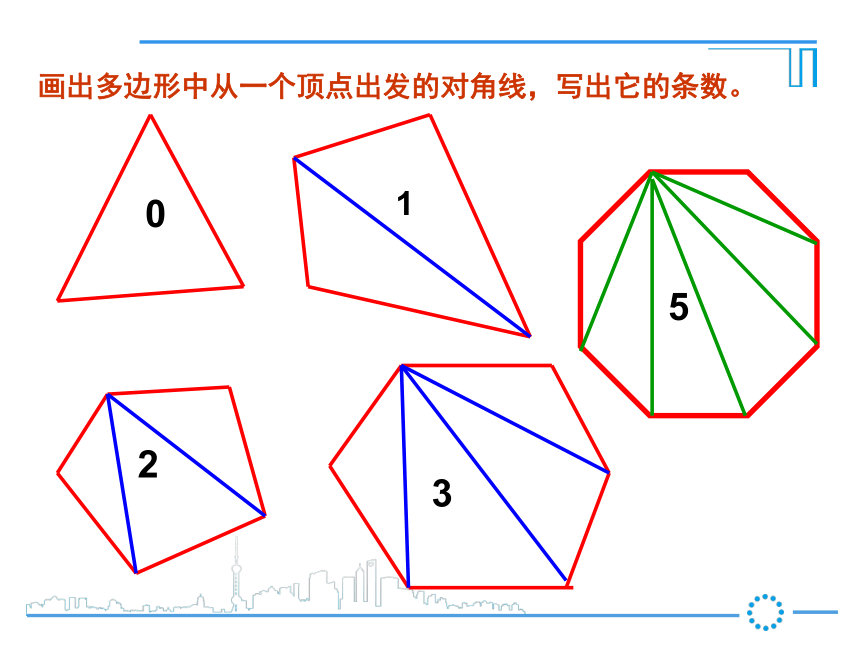
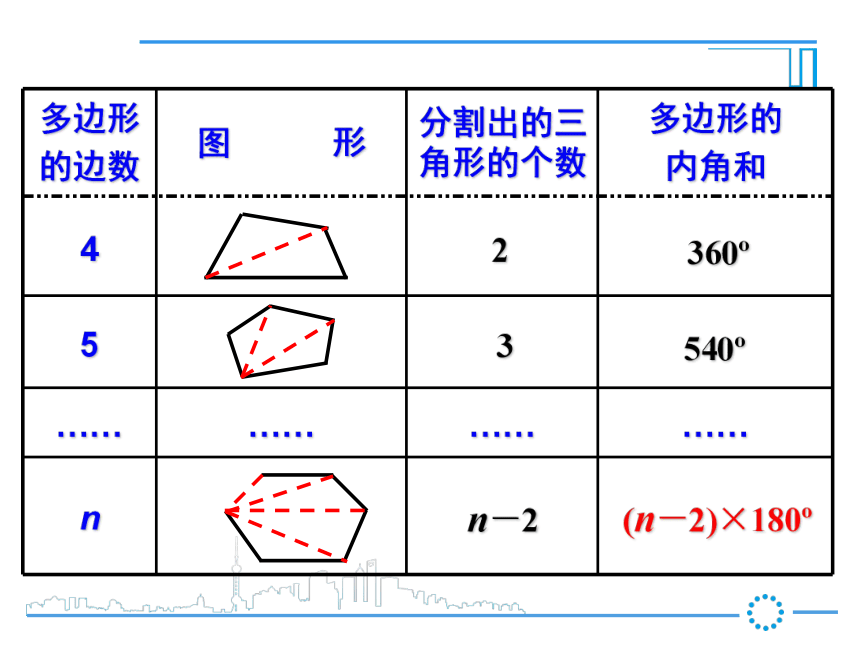
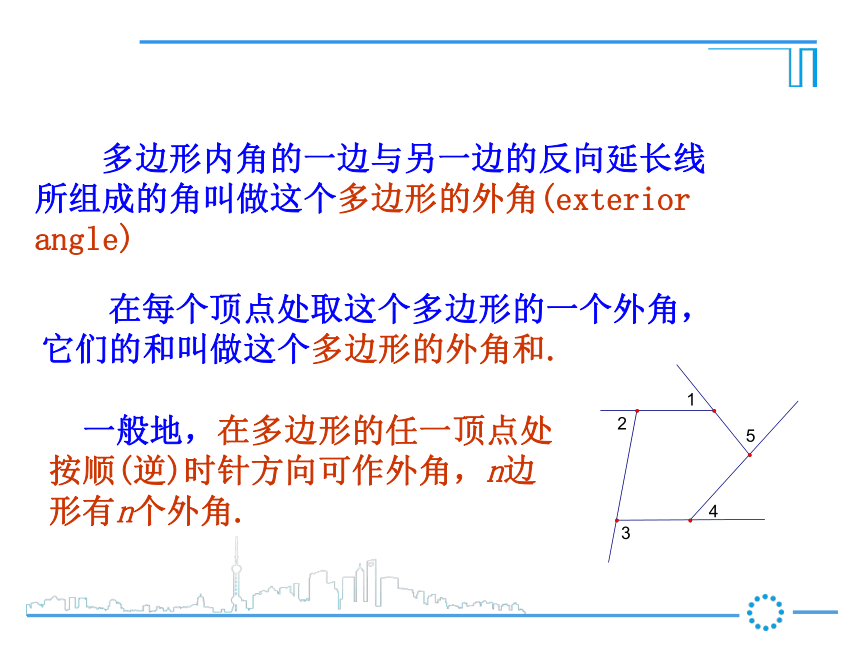
线段首尾顺次相连组成的封闭图形叫做多边形.顶点内角边对角线这里所说的多边形都指凸多边形外角外角获取新知 多边形内角的一边与另一边的反向延长线所组成的角叫多边形的外角. 在每一个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和. 画出多边形中从一个顶点出发的对角线,写出它的条数。01235n-223360o540o(n-2)×180on 边形的内角和公式:n是大于或等于3的自然数 多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角(exterior angle) 在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和. 一般地,在多边形的任一顶点处按顺(逆)时针方向可作外角,n边形有n个外角. 探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
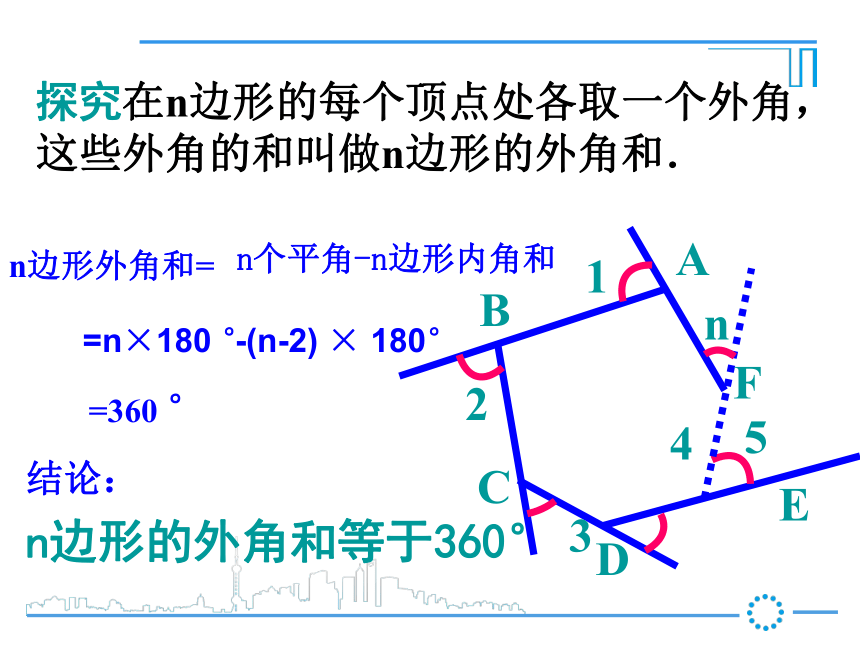
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 ° 过某个多边形一个顶点的所有对角线,
将这个多边形分成5个三角形.这个多边形
是几边形?它的内角和是多少?例1.解:依题意, 这个多边形是七边形,
它的内角和是(7-2) ×180°=900°例2. 如果一个多边形的内角和是1440°, 那么这是 边形。十 解:由n边形的内角和公式可得(n -2)· 180 = 1440 n -2 = 8 n = 10∴这是十边形。 方法小结:
求多边形的边数、
角度的常用方法:
利用公式列方程.
典例解析例3、若正n边形的一个内角是144°,那么n= .解:由n边形的内角和公式可得:(n -2) · 180 = 144n180n – 360 = 144n180n -144n=36036n = 360n = 1010例4、一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 1.一个多边形的外角都等于60°,这个多边形是几边形? 解:因为多边形的外角和等于360°,所以根据题意,可知道这个多边形的边数是:
360÷60=6 .答:这个多边形是六边形. 2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分,这种多边形是几边形?为什么? 解:设:这个正多边形的一个内角为x°,
则由题图得:3x=360°. x=120°.
再根据多边形的内角和公式得:
n×120°=(n-2)×180°. 解得n=6 . 答:(略)巩固提高3、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °4、正五边形的每一个外角等于____,每一个内角等于_____。5x=360°x=72°72°108°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °5、已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6
n 边形的内角和公式:n是大于或等于3的自然数结论:n边形的外角和等于360°。课堂小结P87例3 一个多边形的每一个外角都是720,这个多边形是几边形?P87例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?课堂练习P88练习 1、2题1.教材P88习题9.2 第1、2、3题;
2.完成练习册本课时的习题.课后作业对世界上的一切学问与知识的掌握也并非难事,只要持之以恒地学习,努力掌握规律,达到熟悉的境地,就能融会贯通,运用自如了。 —— 高士其
线段首尾顺次相连组成的封闭图形叫做多边形.顶点内角边对角线这里所说的多边形都指凸多边形外角外角获取新知 多边形内角的一边与另一边的反向延长线所组成的角叫多边形的外角. 在每一个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和. 画出多边形中从一个顶点出发的对角线,写出它的条数。01235n-223360o540o(n-2)×180on 边形的内角和公式:n是大于或等于3的自然数 多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角(exterior angle) 在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和. 一般地,在多边形的任一顶点处按顺(逆)时针方向可作外角,n边形有n个外角. 探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 ° 过某个多边形一个顶点的所有对角线,
将这个多边形分成5个三角形.这个多边形
是几边形?它的内角和是多少?例1.解:依题意, 这个多边形是七边形,
它的内角和是(7-2) ×180°=900°例2. 如果一个多边形的内角和是1440°, 那么这是 边形。十 解:由n边形的内角和公式可得(n -2)· 180 = 1440 n -2 = 8 n = 10∴这是十边形。 方法小结:
求多边形的边数、
角度的常用方法:
利用公式列方程.
典例解析例3、若正n边形的一个内角是144°,那么n= .解:由n边形的内角和公式可得:(n -2) · 180 = 144n180n – 360 = 144n180n -144n=36036n = 360n = 1010例4、一个多边形的内角和等于它的外角和的3倍,它是几边形? 解:设这个多边形是n边形,则它的内角和是(n-2)·180°,外角和等于360°,
所以:(n-2)·180=3×360
解得:n=8
答:这个多边形是八边形. 1.一个多边形的外角都等于60°,这个多边形是几边形? 解:因为多边形的外角和等于360°,所以根据题意,可知道这个多边形的边数是:
360÷60=6 .答:这个多边形是六边形. 2.下图是三个完全相同的正多边形拼成的无缝隙不重叠的图形的一部分,这种多边形是几边形?为什么? 解:设:这个正多边形的一个内角为x°,
则由题图得:3x=360°. x=120°.
再根据多边形的内角和公式得:
n×120°=(n-2)×180°. 解得n=6 . 答:(略)巩固提高3、如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °4、正五边形的每一个外角等于____,每一个内角等于_____。5x=360°x=72°72°108°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °5、已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6
n 边形的内角和公式:n是大于或等于3的自然数结论:n边形的外角和等于360°。课堂小结P87例3 一个多边形的每一个外角都是720,这个多边形是几边形?P87例4 一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?课堂练习P88练习 1、2题1.教材P88习题9.2 第1、2、3题;
2.完成练习册本课时的习题.课后作业对世界上的一切学问与知识的掌握也并非难事,只要持之以恒地学习,努力掌握规律,达到熟悉的境地,就能融会贯通,运用自如了。 —— 高士其
