八年级数学第十六章整章复习水平测试

八年级数学第十六章整章复测试
一、认认真真选，沉着应战！（每小题3分，共30分）
1．三角形的三边长为a，b，c且，则这个三角形是（　　）．
A． 等边三角形　　　　B． 钝角三角形　　　　C．直角三角形　　　　D．锐角三角形
2．下列各组线段中的三个长度①9、12、15；②7、24、25；③；④3a、4a、5a（a>0）；⑤（m，n为正整数，且）其中可以构成直角三角形的有（　　）．
A．5组　　　　B．4组　　　　C．3组　　　　D．2组
3．已知一直角三角形的木板，三边的平方和为1800，则斜边长为（　　）．
A．80m　　　　B．30m　　　　C．90m　　　　D．120m
4．如图1，字母B所代表的正方形的面积是（　　）．
A． 12　　　　B． 13　　　　C．144　　　　D．194
5．在Rt△ABC中，∠C=90°，周长为60，斜边与一条直角边之比为13∶5，则这个三角形三边长分别是（　　）．
A．5、4、3　　　　B．13、12、5　　　　C．10、8、6　　　　D．36、34、10
6．已知一个直角三角形的两边长分别为3和4，则第三边边长的平方是（　　）．
A．25　　　　B．14　　　　C．7　　　　D．7或25
7．Rt△ABC中，∠B=90°，两直角边AB=7，BC=24，在三角形内有一点P到各边的距离相等，则这个距离是（　　）．
A．1　　　　B．3　　　　C．6　　　　D．无法求出
8．在Rt△ABC中，其对应边长a，b，c，∠C=90°，已知，该直角三角形中，两直角边的关系有（　　）．
A．　　　　B．　　　　C．　　　　D．以上都有可能
9．五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（　　）．
10．如图2，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（　　）．
A．2cm　　　　B．3cm　　　　C．4cm　　　　D．5cm
二、仔仔细细填，记录自信！（每小题3分，共30分）
1．在Rt△ABC中，∠C=90°．
（1）若a=5，b=12，则______；
（2）若b=8，c=17，则______．
2．已知直角三角形的两条直角边分别为6cm，8cm，那么斜边上的高为______cm．
3． 若在△ABC中，AB＝5cm，BC＝6cm，BC边上的中线AD＝4cm，则∠ADC的度数是______度．
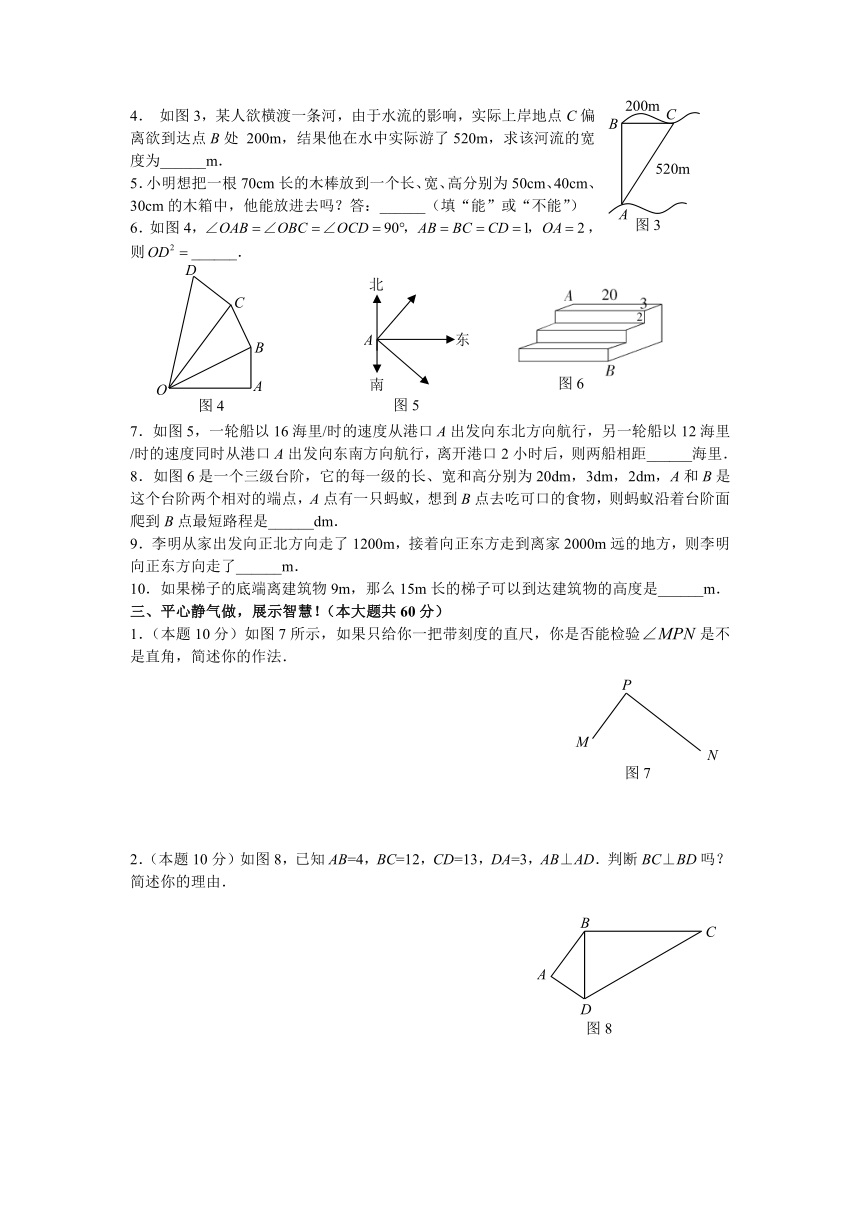
4． 如图3，某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B处 200m，结果他在水中实际游了520m，求该河流的宽度为______m．
5．小明想把一根70cm长的木棒放到一个长、宽、高分别为50cm、40cm、30cm的木箱中，他能放进去吗？答：______（填“能”或“不能”）
6．如图4，，则______．
7．如图5，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距______海里．
8．如图6是一个三级台阶，它的每一级的长、宽和高分别为20dm，3dm，2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是______dm．
9．李明从家出发向正北方向走了1200m，接着向正东方走到离家2000m远的地方，则李明向正东方向走了______m．
10．如果梯子的底端离建筑物9m，那么15m长的梯子可以到达建筑物的高度是______m．
三、平心静气做，展示智慧！（本大题共60分）
1．（本题10分）如图7所示，如果只给你一把带刻度的直尺，你是否能检验是不是直角，简述你的作法．
2．（本题10分）如图8，已知AB=4，BC=12，CD=13，DA=3，AB⊥AD．判断BC⊥BD吗？简述你的理由．
3．（本题12分）如图9，铁路上A，B两点相距25km，C，D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E站的距离相等，则E站应建在离A站多少千米处？
4．（本题13分）如图10，将断落的电话线拉直，使其一端在电杆顶端A处，另一端落在地面C处，这时测得BC=6米；再把电话线沿电杆拉址，使AD=AB，并量出电话线剩余部分（即CD）的长2米，你能由此算出电杆AB的高吗？
5．（本题15分）如图11，沿OA将圆锥侧面剪开，展开成平面图形是扇形OAB．
（1）扇形的弧的长与圆锥底面圆周的长是怎样的关系？点A和点B在圆锥的侧面上是怎样的位置关系？
（2）若角∠AOB=90°，则圆锥底面圆半径r与扇形OAB的半径R之间有怎样的关系？
（3）若点A在圆锥侧面上运动一圈后又回到原位，，且∠AOB=90°，求点A运动的最短路程．
参考答案
一、1～5．CBBCD 6～10．DBCCB
二、1．（1）13　（2）60 2．4.8 3．90 4．480 5．能
6．7 　7．40 　8．25 　9．1600 　10．12
三、1．略．
2．在Rt△ABD中，有，即．
在△DBC中，．
所以，即．
3．10千米．
4．8米．
5．（1）扇形弧AB的长于圆锥的底面周长相等，点A和点B在圆锥的侧面上重合．
（2）圆锥的底面周长=．
弧AB的长度为．
依题意，得，即R=4r．
（3）点A运动的最短路程为1．
东
南
北
A
图5
O
D
C
B
A
图4
A
A
B
D
C
图2
E
A
B
D
C
图8
B
A
C
D
图10
A
B
O
图11
图1
25
169
B
B
C
图3
520m
200m
图6
D
C
A
B
图9
图7
M
P
N