【新学期备课参考】2014-2015学年华师大版七年级数学下册:第九章 多边形 复习课件(共19张ppt)
文档属性
| 名称 | 【新学期备课参考】2014-2015学年华师大版七年级数学下册:第九章 多边形 复习课件(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1004.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-29 15:30:33 | ||
图片预览



文档简介
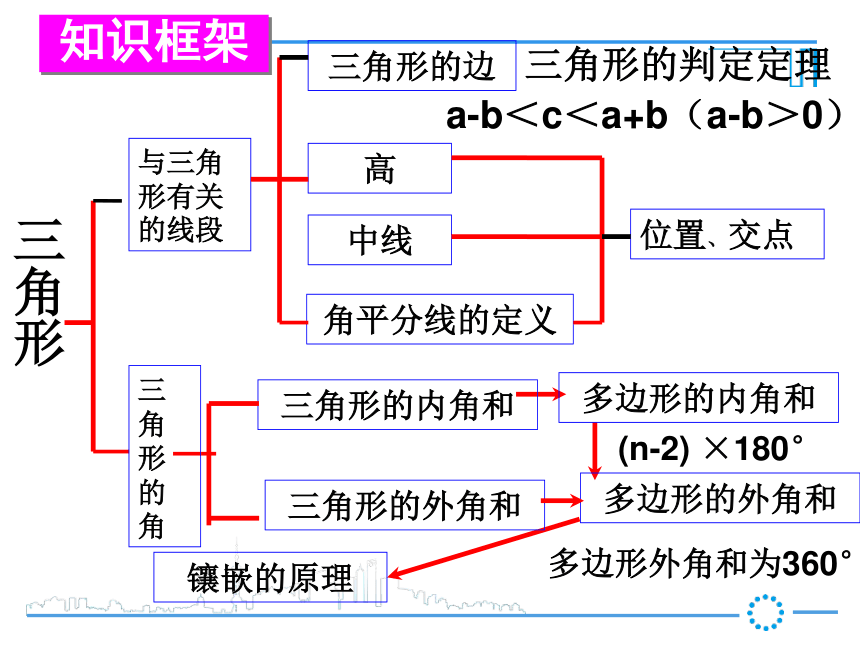
课件19张PPT。章末复习华东师大·七年级下册(n-2) ×180°三角形与三角形有关的线段a-b<c<a+b(a-b>0)高三角形的边三角形的判定定理中线角平分线的定义位置、交点三角形的内角和多边形的内角和多边形的外角和三角形的外角和多边形外角和为360°镶嵌的原理三角形的角知识框架1.三角形三边的关系
三角形三边的关系为:三角形任意两边之和大于第三边;由此我们还可推得:三角形任意两边的之差小于第三边. 知识回顾2.关于三角形的分类
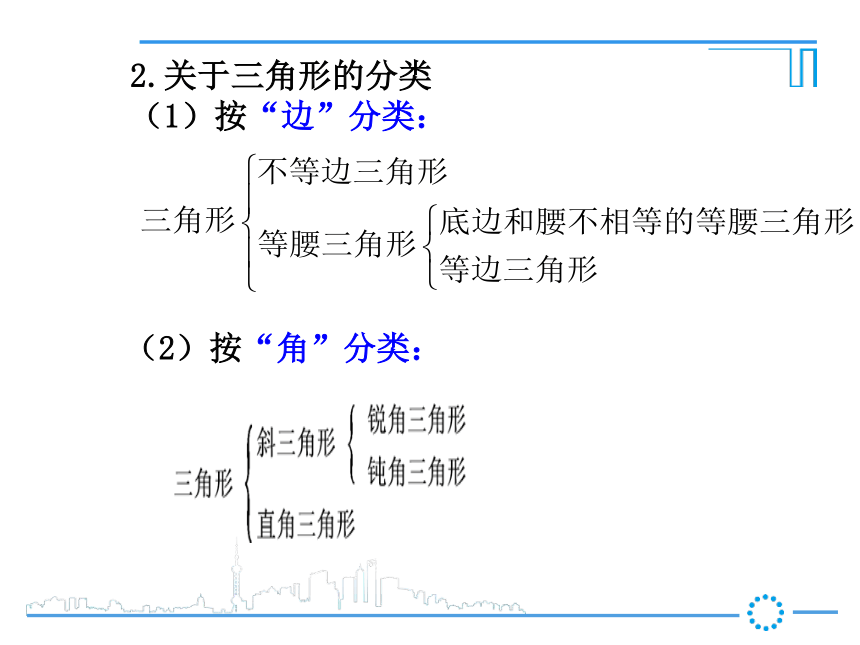
(1)按“边”分类:
(2)按“角”分类:
3. 添加辅助线
学习数学知识的一个基本思想就是转化思想,把复杂的、未知的问题转化为简单的、熟悉的或已经解决的问题.很多几何题往往需要添加辅助线才能进行这种转化,作辅助线时应考虑以下几个方面:
(1)充分利用条件,体现条件集中的原则,充分揭示题目中的各个条件间的不明显的关系;
(2)恰当的转化条件;
(3)恰当转化结论。1.正多边形的定义:
2.凸多边形的辨认:
3.n 边形:
(1)从一个顶点出发可引_____条对角线,可分___
个三角形
(2)总共有________对角线
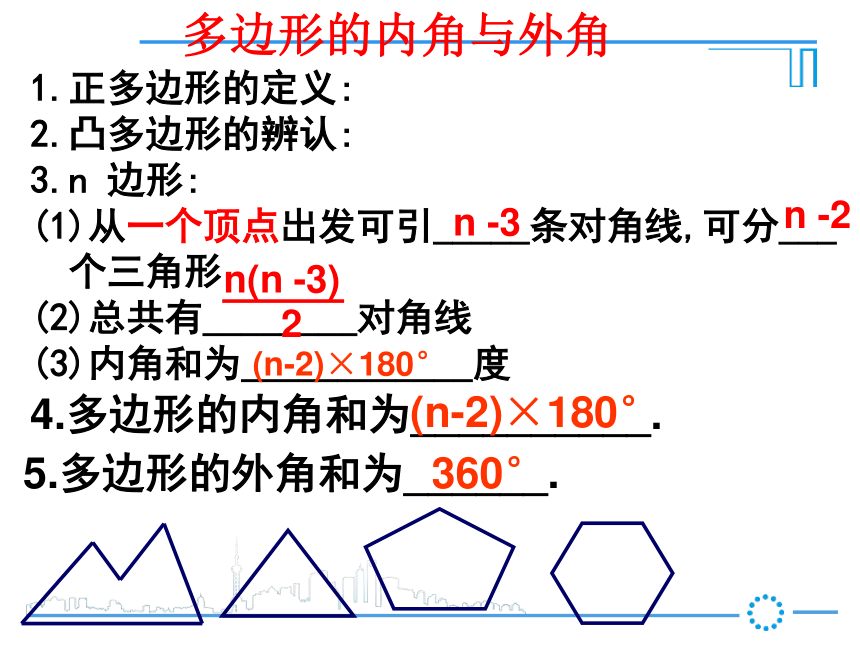
(3)内角和为____________度多边形的内角与外角
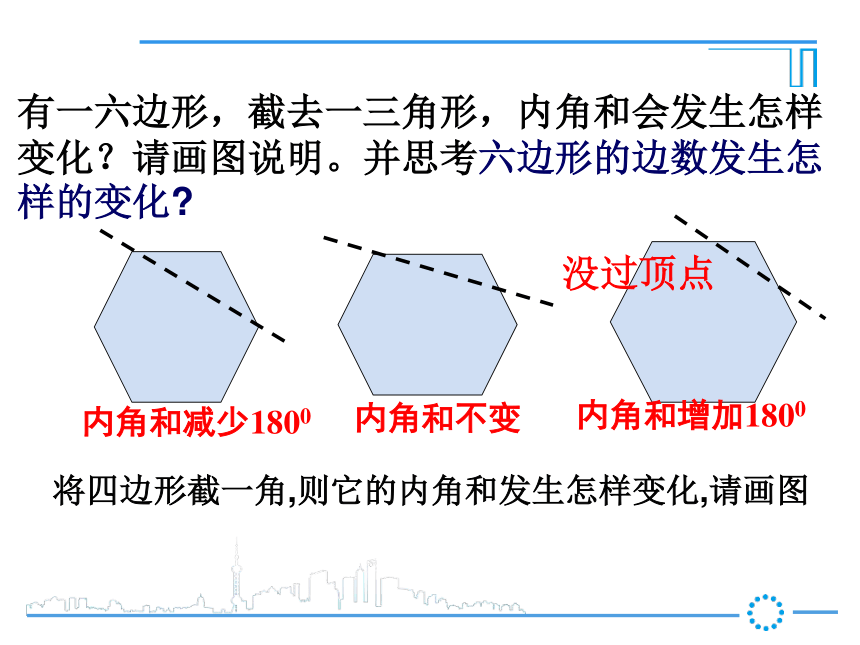
5.多边形的外角和为______.360°4.多边形的内角和为__________.(n-2)×180°n -3n -2(n-2)×180°有一六边形,截去一三角形,内角和会发生怎样变化?请画图说明。并思考六边形的边数发生怎样的变化?
内角和减少1800内角和不变内角和增加1800将四边形截一角,则它的内角和发生怎样变化,请画图没过顶点1.已知三角形的三边长分别是3,8,,若的值为偶数,则
A.6个 B.5个 C.4个 D.3个D随堂演练的值有 ( ).2.下列关于三角形按边分类的集合中,正确的是: D 3. 三角形周长为10,其中有两边相等且长
为整数,则第三边长为_________.4. 已知:如图,AB∥CD,∠B =45°,∠BED=78°,求∠D的度数.
解:如图,延长BE交CD于点F,
∵AB∥CD,∠B=45°,
∴∠1=∠B=45°,
∴∠D=∠BED-∠1=78°-45°=33°分析: 要按△ABC为锐角三角形和钝角三角形两种情况,分类讨论.
解:分两种情况讨论:
(1)当△ABC为锐角
三角形时,如图所示,在
△ABD中,
∵ BD是AC边上的高
∴ ∠ADB=90°5. 在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数是多少?
又∵ ∠ABD=30°
∴ ∠A=180°-∠ADB
-∠ABD=180°-90°-30°=60°.
又∵ ∠A+∠ABC+∠C=180°
∴ ∠ABC+∠C=120°,
又∵ ∠ABC=∠C,∴ ∠C=60°.
(2)当△ABC为钝角三角
形时,如图所示.在直
角△ABD中,
∵ ∠ABD=30°
所以∠BAD=60°.∴ ∠BAC=120°.
又∵ ∠BAC+∠ABC+∠C=180°
∴ ∠ABC+∠C=60°.
∴ ∠C=30°.
综上所知,∠C的度数为60°或30°. 五边形内角和为
4×180°-180°=540°五边形内角和为
5 ×180°-360° =540°ABCEO6.如下图:你能求五边形内角和吗??A.六边形 B.七边形 C.十边形 D.十一边形7.一个多边形有14条对角线,则它是_____边形B8、如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数。 12解:连接BE,
∵∠C+∠D+∠COD=∠1+∠2+∠BOE
∴ ∠C+∠D= ∠1+∠2
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠1+∠2+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F
=360o
课堂小结通过本节课的复习你有哪些收获?1.教材P94复习题;
2.完成练习册本课时的习题.课后作业学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。 —— 毛泽东
三角形三边的关系为:三角形任意两边之和大于第三边;由此我们还可推得:三角形任意两边的之差小于第三边. 知识回顾2.关于三角形的分类
(1)按“边”分类:
(2)按“角”分类:
3. 添加辅助线
学习数学知识的一个基本思想就是转化思想,把复杂的、未知的问题转化为简单的、熟悉的或已经解决的问题.很多几何题往往需要添加辅助线才能进行这种转化,作辅助线时应考虑以下几个方面:
(1)充分利用条件,体现条件集中的原则,充分揭示题目中的各个条件间的不明显的关系;
(2)恰当的转化条件;
(3)恰当转化结论。1.正多边形的定义:
2.凸多边形的辨认:
3.n 边形:
(1)从一个顶点出发可引_____条对角线,可分___
个三角形
(2)总共有________对角线
(3)内角和为____________度多边形的内角与外角
5.多边形的外角和为______.360°4.多边形的内角和为__________.(n-2)×180°n -3n -2(n-2)×180°有一六边形,截去一三角形,内角和会发生怎样变化?请画图说明。并思考六边形的边数发生怎样的变化?
内角和减少1800内角和不变内角和增加1800将四边形截一角,则它的内角和发生怎样变化,请画图没过顶点1.已知三角形的三边长分别是3,8,,若的值为偶数,则
A.6个 B.5个 C.4个 D.3个D随堂演练的值有 ( ).2.下列关于三角形按边分类的集合中,正确的是: D 3. 三角形周长为10,其中有两边相等且长
为整数,则第三边长为_________.4. 已知:如图,AB∥CD,∠B =45°,∠BED=78°,求∠D的度数.
解:如图,延长BE交CD于点F,
∵AB∥CD,∠B=45°,
∴∠1=∠B=45°,
∴∠D=∠BED-∠1=78°-45°=33°分析: 要按△ABC为锐角三角形和钝角三角形两种情况,分类讨论.
解:分两种情况讨论:
(1)当△ABC为锐角
三角形时,如图所示,在
△ABD中,
∵ BD是AC边上的高
∴ ∠ADB=90°5. 在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数是多少?
又∵ ∠ABD=30°
∴ ∠A=180°-∠ADB
-∠ABD=180°-90°-30°=60°.
又∵ ∠A+∠ABC+∠C=180°
∴ ∠ABC+∠C=120°,
又∵ ∠ABC=∠C,∴ ∠C=60°.
(2)当△ABC为钝角三角
形时,如图所示.在直
角△ABD中,
∵ ∠ABD=30°
所以∠BAD=60°.∴ ∠BAC=120°.
又∵ ∠BAC+∠ABC+∠C=180°
∴ ∠ABC+∠C=60°.
∴ ∠C=30°.
综上所知,∠C的度数为60°或30°. 五边形内角和为
4×180°-180°=540°五边形内角和为
5 ×180°-360° =540°ABCEO6.如下图:你能求五边形内角和吗??A.六边形 B.七边形 C.十边形 D.十一边形7.一个多边形有14条对角线,则它是_____边形B8、如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数。 12解:连接BE,
∵∠C+∠D+∠COD=∠1+∠2+∠BOE
∴ ∠C+∠D= ∠1+∠2
∴∠A+∠ABC+∠C+∠D+∠DEF+∠F
=∠A+∠ABC+∠1+∠2+∠DEF+∠F
=∠A+∠ABE+∠BEF+∠F
=360o
课堂小结通过本节课的复习你有哪些收获?1.教材P94复习题;
2.完成练习册本课时的习题.课后作业学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。 —— 毛泽东
