八年级上册第十六章《勾股定理》整章水平测试(B)
文档属性
| 名称 | 八年级上册第十六章《勾股定理》整章水平测试(B) |

|
|
| 格式 | rar | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-22 00:00:00 | ||
图片预览

文档简介
八年级上册第十六章《勾股定理》整章水平测试(B)
河北 刘新民
一、认认真真选,沉着应战!(每小题3分,共30分)
1. 给出下列几组数:
(1)6、7、8;(2)8、15、6;(3);(4)
其中能组成直角三角形的三条边长是( )
A.(1)(3) B.(2)(4) C.(1)(2) D.(3)(4)
2. 直角三角形的周长为12 cm,斜边长为5 cm,则其面积为( )
A.12 cm2 B.6 cm2 C.8 cm2 D.10 cm2
3.正方形的对角线长是18,则这个正方形的面积是( )
A.9 B.18 C.162 D.81
4.一等腰三角形底边长为,腰长为,则腰上的高为( )
A. B. C. D.
5.设a、b都是正整数,且a-b,3b,a+b(a>2b)构成一个直角三角形三边的长,则这个三角形的任一边的长不可能是( )
A.12 B.13 C.14 D.15
6.男孩戴维是城里的飞盘冠军,戈里是城里最可恶的踩高跷的人,两人约定一比高低.戴维直立肩高1米,他投飞盘很有力,但需在13米内才有威力;戈里踩高跷时鼻子离地13米,他的鼻子是他惟一的弱点.戴维需离戈里( )远时才能击中对方的鼻子而获胜.
A. 7米 B.8米 C. 6米 D.5米
7. 若a、b、c为△ABC的三边长,且满足a2+ab-ac-bc=0,b2+bc-ba-ca=0,则△ABC的形状是( )
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
8.如图,将三边长分别为3、4、5的,沿最长边翻转成
,则的长为( )
A. B. C. D.
9.直角三角形的两条直角边长为,斜边上的高为,则下列各式中总能成立的是 ( )
A. B. C. += D. +=
10.已知,,,,则以为边的三角形( )
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.一定不是直角三角形
二、仔仔细细填,记录自信!(每小题3分,共30分)
1.在△ABC中,若c=m+n,a=m-n,当b2=____________时,∠C=90.
2.在长、宽、高分别为1 dm、2 dm、2 dm的长方体箱子内能放入的最长物体的长度是______ dm.
3. 如图,在一棵树的10米高B处有两只猴子,一只猴子爬下树走到离
树20米处的池塘的A处.另一只爬到树顶D后直接跃到A处, 距离
以直线计算,如果两只猴子所经过的距离相等,则这棵树高____米.
4. 如果a︰c=3︰5,c=10 cm,那么斜边c上的高h=____________.
5. 如图,在中,,,,
则 _______.
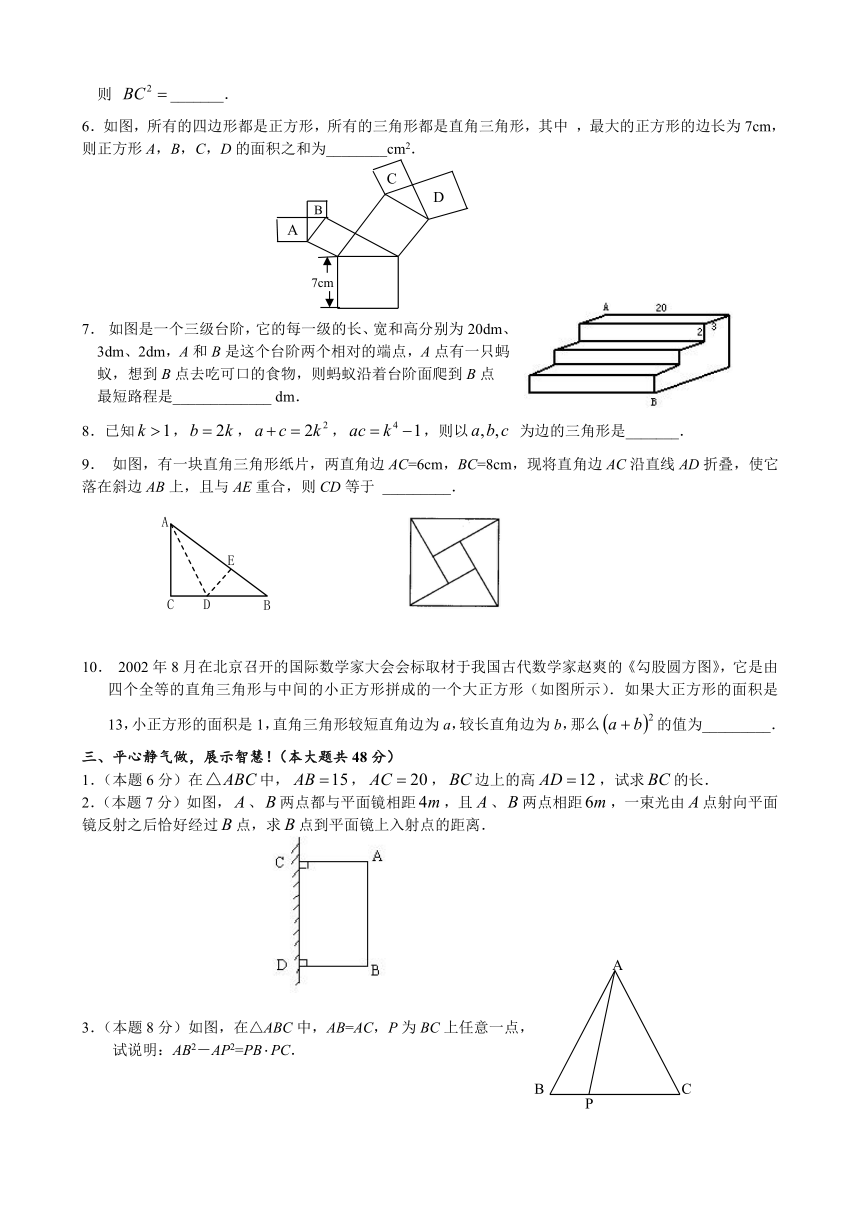
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 ,最大的正方形的边长为7cm, 则正方形A,B,C,D的面积之和为________cm2.
7. 如图是一个三级台阶,它的每一级的长、宽和高分别为20dm、
3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂
蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点
最短路程是_____________ dm.
8.已知,,,,则以 为边的三角形是_______.
9. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于 _________.
10. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形较短直角边为a,较长直角边为b,那么的值为_________.
三、平心静气做,展示智慧!(本大题共48分)
1.(本题6分)在中,,,边上的高,试求的长.
2.(本题7分)如图,、两点都与平面镜相距,且、两点相距,一束光由点射向平面镜反射之后恰好经过点,求点到平面镜上入射点的距离.
3.(本题8分)如图,在△ABC中,AB=AC,P为BC上任意一点,
试说明:AB2-AP2=PBPC.
4.(本题8分)观察下列表格:
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
…… ……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
5.(本题9分)阅读下面的解题过程:
已知a、b、c分别为△ABC的三边,且满足,试判断△ABC的形状.
解:因为 ①
所以 ②
所以 ③
所以△ABC是直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:____________.
(2)错误的原因是__________________________________.
(3)本题的正确结论是____________________________________.
6.(本题10分)如图所示,高速公路的同一侧有A、B两个村庄,它们到高速公路所在直线MN的距离分别是,.要在高速公路上、之间设一个出口,使A、B两个村庄到的距离之和最短,这个最短距离是多少?
四、发散思维,游刃有余!(本题12分)
出入相补原理是我国著名数学家吴文俊先生提出的,他认为这个原理“就是指这样的明显事实:一个平面图形从一处移到他处,面积不变.又若把图形分割成若干块,那么各部分面积的和等于原来图形的面积,因而图形移置前后诸面积间的和、差有简单的相等关系.立体的情形也是如此”.
我们教材中介绍的勾股定理的证明就用到了出入相补原理.
下面我们再介绍刘徽的一种证明勾股定理的方法:如图,正方形ABCD、BFGI的边长分别为b、a,在BF上取一点E,使AE=a,连结DE、GE,将△ADE移至△CDH,将△EFG移至△HIG,由此就可以证明勾股定理,你试一试吧!
参考答案
一、1—5:DBCCC 6—10:DDDDC
二、 1.4mn
2.3
3.15
4.4.8 cm
5. 6
6.49
7. 25
8.直角三角形
9.
10.25
三、
1.(1)当边上的高在的内部时,由勾股定理,得,,
则;
(2)当边上的高在的外部时同理由勾股定理可求得,,这时,.故的长为25或7.
2.作出点关于的对称点,连结,交于点,则点即为光的入射点.连结,在中,由勾股定理,得.
3.作于,则,
.又
即AB2-AP2=PBPC
4.显然所得到的各组数都为勾股数,所以可列出等式整理得,所以.由 可求得.
答案:.
5.(1)C;(2)可以为零;(3)△ABC是直角三角形或等腰三角形.
6.过B点作关于直线MN的对称点,连结交于点P, 则,易知P点即为到A、B距离之和最短的点.过A作于点E,则,,由勾股定理知,,即 故最短出口到A、B两个村庄的距离之和为10.
四、 四边形DEGH是以△ADE的斜边为边的正方形,其面积等于正方形ABCD、BFGI的面积和,即勾股定理得证.
C
B
A
7cm
D
C
B
A
D
B
C
A
A
B
P
C
河北 刘新民
一、认认真真选,沉着应战!(每小题3分,共30分)
1. 给出下列几组数:
(1)6、7、8;(2)8、15、6;(3);(4)
其中能组成直角三角形的三条边长是( )
A.(1)(3) B.(2)(4) C.(1)(2) D.(3)(4)
2. 直角三角形的周长为12 cm,斜边长为5 cm,则其面积为( )
A.12 cm2 B.6 cm2 C.8 cm2 D.10 cm2
3.正方形的对角线长是18,则这个正方形的面积是( )
A.9 B.18 C.162 D.81
4.一等腰三角形底边长为,腰长为,则腰上的高为( )
A. B. C. D.
5.设a、b都是正整数,且a-b,3b,a+b(a>2b)构成一个直角三角形三边的长,则这个三角形的任一边的长不可能是( )
A.12 B.13 C.14 D.15
6.男孩戴维是城里的飞盘冠军,戈里是城里最可恶的踩高跷的人,两人约定一比高低.戴维直立肩高1米,他投飞盘很有力,但需在13米内才有威力;戈里踩高跷时鼻子离地13米,他的鼻子是他惟一的弱点.戴维需离戈里( )远时才能击中对方的鼻子而获胜.
A. 7米 B.8米 C. 6米 D.5米
7. 若a、b、c为△ABC的三边长,且满足a2+ab-ac-bc=0,b2+bc-ba-ca=0,则△ABC的形状是( )
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
8.如图,将三边长分别为3、4、5的,沿最长边翻转成
,则的长为( )
A. B. C. D.
9.直角三角形的两条直角边长为,斜边上的高为,则下列各式中总能成立的是 ( )
A. B. C. += D. +=
10.已知,,,,则以为边的三角形( )
A.一定是等边三角形 B.一定是等腰三角形
C.一定是直角三角形 D.一定不是直角三角形
二、仔仔细细填,记录自信!(每小题3分,共30分)
1.在△ABC中,若c=m+n,a=m-n,当b2=____________时,∠C=90.
2.在长、宽、高分别为1 dm、2 dm、2 dm的长方体箱子内能放入的最长物体的长度是______ dm.
3. 如图,在一棵树的10米高B处有两只猴子,一只猴子爬下树走到离
树20米处的池塘的A处.另一只爬到树顶D后直接跃到A处, 距离
以直线计算,如果两只猴子所经过的距离相等,则这棵树高____米.
4. 如果a︰c=3︰5,c=10 cm,那么斜边c上的高h=____________.
5. 如图,在中,,,,
则 _______.
6.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中 ,最大的正方形的边长为7cm, 则正方形A,B,C,D的面积之和为________cm2.
7. 如图是一个三级台阶,它的每一级的长、宽和高分别为20dm、
3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂
蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点
最短路程是_____________ dm.
8.已知,,,,则以 为边的三角形是_______.
9. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于 _________.
10. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形较短直角边为a,较长直角边为b,那么的值为_________.
三、平心静气做,展示智慧!(本大题共48分)
1.(本题6分)在中,,,边上的高,试求的长.
2.(本题7分)如图,、两点都与平面镜相距,且、两点相距,一束光由点射向平面镜反射之后恰好经过点,求点到平面镜上入射点的距离.
3.(本题8分)如图,在△ABC中,AB=AC,P为BC上任意一点,
试说明:AB2-AP2=PBPC.
4.(本题8分)观察下列表格:
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
…… ……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值.
5.(本题9分)阅读下面的解题过程:
已知a、b、c分别为△ABC的三边,且满足,试判断△ABC的形状.
解:因为 ①
所以 ②
所以 ③
所以△ABC是直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号:____________.
(2)错误的原因是__________________________________.
(3)本题的正确结论是____________________________________.
6.(本题10分)如图所示,高速公路的同一侧有A、B两个村庄,它们到高速公路所在直线MN的距离分别是,.要在高速公路上、之间设一个出口,使A、B两个村庄到的距离之和最短,这个最短距离是多少?
四、发散思维,游刃有余!(本题12分)
出入相补原理是我国著名数学家吴文俊先生提出的,他认为这个原理“就是指这样的明显事实:一个平面图形从一处移到他处,面积不变.又若把图形分割成若干块,那么各部分面积的和等于原来图形的面积,因而图形移置前后诸面积间的和、差有简单的相等关系.立体的情形也是如此”.
我们教材中介绍的勾股定理的证明就用到了出入相补原理.
下面我们再介绍刘徽的一种证明勾股定理的方法:如图,正方形ABCD、BFGI的边长分别为b、a,在BF上取一点E,使AE=a,连结DE、GE,将△ADE移至△CDH,将△EFG移至△HIG,由此就可以证明勾股定理,你试一试吧!
参考答案
一、1—5:DBCCC 6—10:DDDDC
二、 1.4mn
2.3
3.15
4.4.8 cm
5. 6
6.49
7. 25
8.直角三角形
9.
10.25
三、
1.(1)当边上的高在的内部时,由勾股定理,得,,
则;
(2)当边上的高在的外部时同理由勾股定理可求得,,这时,.故的长为25或7.
2.作出点关于的对称点,连结,交于点,则点即为光的入射点.连结,在中,由勾股定理,得.
3.作于,则,
.又
即AB2-AP2=PBPC
4.显然所得到的各组数都为勾股数,所以可列出等式整理得,所以.由 可求得.
答案:.
5.(1)C;(2)可以为零;(3)△ABC是直角三角形或等腰三角形.
6.过B点作关于直线MN的对称点,连结交于点P, 则,易知P点即为到A、B距离之和最短的点.过A作于点E,则,,由勾股定理知,,即 故最短出口到A、B两个村庄的距离之和为10.
四、 四边形DEGH是以△ADE的斜边为边的正方形,其面积等于正方形ABCD、BFGI的面积和,即勾股定理得证.
C
B
A
7cm
D
C
B
A
D
B
C
A
A
B
P
C
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
