第16章《勾股定理》水平测试（C）

第16章《勾股定理》水平测试（C）
江苏 刘东升
一、精心选一选，相信你一定能选对！（每题3分，共30分）
1．已知△ABC中，∠A=∠B=∠C，则它的三条边之比为（ ）．
A．1：1： B．1：：2 C．1：： D．1：4：1
2．已知直角三角形一个锐角60°，斜边长为1，那么此直角三角形的周长是（ ）．
A． B．3 C． D．
3．下列各组线段中，能够组成直角三角形的是（ ）．
A．6，7，8 B．5，6，7 C．4，5，6 D．3，4，5
4．下列各命题的逆命题成立的是（ ）
A．全等三角形的对应角相等
B．如果两个数相等，那么它们的绝对值相等
C．两直线平行，同位角相等
D．如果两个角都是45°，那么这两个角相等
5．若等边△ABC的边长为2cm，那么△ABC的面积为（ ）．
A．cm2 B．2cm2 C．3cm2 D．4cm2
6．在Rt△ABC中，已知其两直角边长a=1，b=3，那么斜边c的长为（ ）．
A．2 B．4 C．2 D．
7．如图所示，△ABC中，CD⊥AB于D，若AD=2BD，AC=5，BC=4，则BD的长为（ ）．
A． B． C．1 D．
8．下面四组数中是勾股数的有（ ）．
（1）1.5，2.5，2 （2），，2
（3）12，16，20 （4）0.5，1.2，1.3
A．1组 B．2组 C．3组 D．4组
9．直角三角形有一条直角边长为13，另外两条边长都是自然数，则周长为（ ）．
A．182 B．183 C．184 D．185
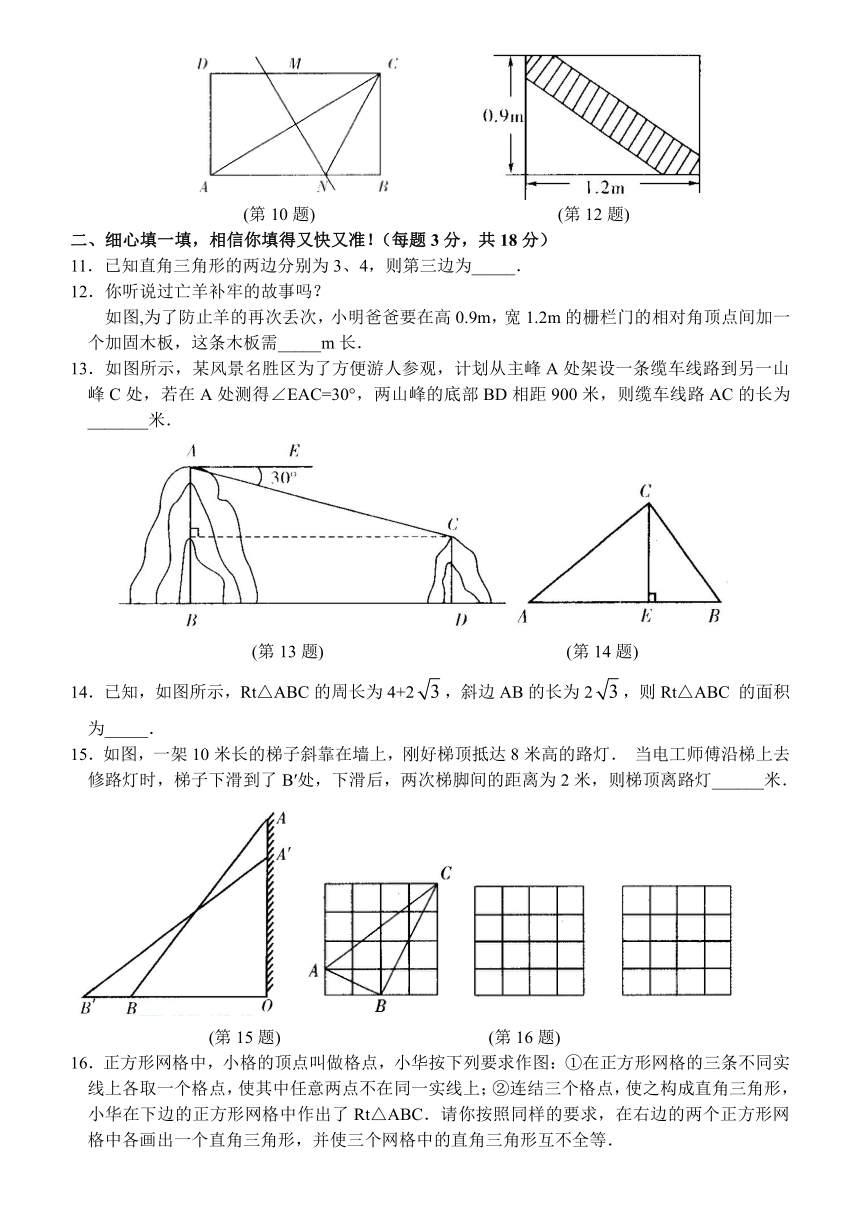
10．如图，长方形ABCD中，AB=4，BC=3，将其沿直线MN折叠，使点C与点A重合，则CN的长为（ ）．
A． B． C． D．
(第10题) (第12题)
二、细心填一填，相信你填得又快又准！（每题3分，共18分）
11．已知直角三角形的两边分别为3、4，则第三边为_____．
12．你听说过亡羊补牢的故事吗？
如图,为了防止羊的再次丢次，小明爸爸要在高0.9m，宽1.2m的栅栏门的相对角顶点间加一个加固木板，这条木板需_____m长．
13．如图所示，某风景名胜区为了方便游人参观，计划从主峰A处架设一条缆车线路到另一山峰C处，若在A处测得∠EAC=30°，两山峰的底部BD相距900米，则缆车线路AC的长为_______米．
(第13题) (第14题)
14．已知，如图所示，Rt△ABC的周长为4+2，斜边AB的长为2，则Rt△ABC的面积为_____．
15．如图，一架10米长的梯子斜靠在墙上，刚好梯顶抵达8米高的路灯．当电工师傅沿梯上去修路灯时，梯子下滑到了B′处，下滑后，两次梯脚间的距离为2米，则梯顶离路灯______米．
(第15题) (第16题)
16．正方形网格中，小格的顶点叫做格点，小华按下列要求作图：①在正方形网格的三条不同实线上各取一个格点，使其中任意两点不在同一实线上；②连结三个格点，使之构成直角三角形，小华在下边的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．
三、耐心选一选，千万别漏选！（每题4分，共8分，错选一项得0分，对而不全酌情给分）
17．在Rt△ABC中，∠C=90°，∠A=30°，则下列结论中正确的是（ ）。
A．AB=2BC B．AB=2AC C．AC2+AB2=BC2 D．AC2+BC2=AB2
18．在Rt△ABC中，若AC=，BC=，AB=3，则下列结论中不正确的是（ ）。
A．∠C=90° B．∠B=90°
C．△ABC是锐角三角形 D．△ABC是钝角三角形
四、仔细想一想，相信你一定行！
19．（8分）如图，在一棵树的10米高B处有两只猴子，其中一只爬下树走向离树20米的池塘C，而另一只爬到树顶D后直扑池塘C，结果两只猴子经过的距离相等，问这棵树有多高？
20．（8分）已知，如图所示，折叠长方形的一边AD，使点D落在BC边的点F处，如果AB=8cm，BC=10cm，求EC的长．
21．（8分）某校把一块形状为直角三角形的废地开辟为生物园，如图所示，∠ACB=90°，AC=80米，BC=60米，若线段CD是一条小渠，且D点在边AB上，已知水渠的造价为10元/米，问D点在距A点多远处时，水渠的造价最低？最低造价是多少？
22．（9分）细心观察下图，认真分析各式，然后解答问题．
（）2+1=2 S1=
（）2+1=3 S2=
（）2+4=5 S3=
（1）请用含n（n是正整数）的等式表示上述变化规律；
（2）推算出OA10的长；
（3）求出S12+S22+S22+…+S102的值．
23．（9分）如图，正方形MNPQ网格中，每个小方格的边长都相等，正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上．
（1）设正方形MNPQ网格内的每个小方格的边长为1，求：
①△ABQ，△BCM，△CDN，△ADP的面积；
②正方形ABCD的面积．
（2）设MB=a，BQ=b，利用这个图形中的直角三角形和正方形的面积关系，你能验证已学过的哪一个数学公式或定理吗？相信你能给出简明的推理过程．
五、认真做一做，展示你的应用能力！
24．（12分）（1）四年一度的国际数学家大会于2002年8月20日在北京召开，大会会标如图（1）．它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积为13，每个直角三角形两直角边的和是5，求中间小正方形的面积．
（2）现有一张长为6.5cm，宽为2cm的纸片，如图（2），请你将它分割成6块，再拼合成一个正方形．
（要求：先在图（2）中画出分割线，再画出拼成的正方形并标明相应数据）
25．（10分）如图，A市气象站测得台风中心在A市正东方向300千米的B处，以10 千米/时的速度向北偏西60°的BF方向移动，距台风中心200千米范围内是受台风影响的区域．
（1）A市是否会受到台风的影响？写出你的结论并给予说明；
（2）如果A市受这次台风影响，那么受台风影响的时间有多长？
参考答案:
1．B 2．D 3．D 4．C 5．A 6．D 7．A 8．A 9．A 10．B
11．5或 12．1．5 13．600 14．1 15．2 16．略 17．AD
18．BCD 19．树高15m． 提示：BD=x，则（30-x）2-（x+10）2=202
20．连结AE，则△ADE≌△AFE，所以AF=AD=10，DE=EF．
设CE=x，则EF=DE=8-x，BF==6，CF=4．
在Rt△CEF中，EF2=CE2+CF2，即（8-x）2=x2+16，故x=3
21．当CD为斜边上的高时，CD最短，从而水渠造价最价
∵CD·AB=AC·BC ∴CD==48米
∴AD==64米
所以，D点在距A点64米的地方，水渠的造价最低，其最低造价为480元．
22．（1）Sn=·1= （2）OA10=
（3）S12+S22+…+S102=（）2+（）2+（）2…+（）2
=（1+2+…+10）=．
23．（1）①S△ABQ=S△BCM=S△CDN=S△ADP=6
②S正方形ABCD=S正方形MNPQ-4S△ABQ=25
（2）勾股定理或完全平方公式或平方差公式，推理过程略．
24．（1）设直角三角形的两条边分别为a、b（a>b），则依题意有：
①2-②，得ab=6，（a-b）2=（a+b）2-4ab=1，
∴a-b=1，故小正方形的面积为1.
(2)
25．（1）过A作AC⊥BF于C，则AC=AB=150<200，
∴A市会受到台风影响．
（2）过A作AD=200km，交BF于点D．
∴DC==50，
∴该市受台风影响的时间为：=10小时．