北师大版数学七年级上册2.4 有理数的加法(第1课时)课件(共26张PPT)
文档属性
| 名称 | 北师大版数学七年级上册2.4 有理数的加法(第1课时)课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 19:50:39 | ||
图片预览






文档简介
(共26张PPT)
第1课时
北师大版 数学 七年级上册
4 有理数的加法
第二章 有理数及其运算
学习目标
1.了解有理数加法的意义,理解有理数加法法则的合理性;
2.掌握有理数加法法则,并能运用法则进行计算;(重点)
3.经历探究有理数加法法则的过程,深刻感受分类讨论、数形结合的思想,感受由具体到抽象、由特殊到一般的认知规律。(难点)
一、导入新课
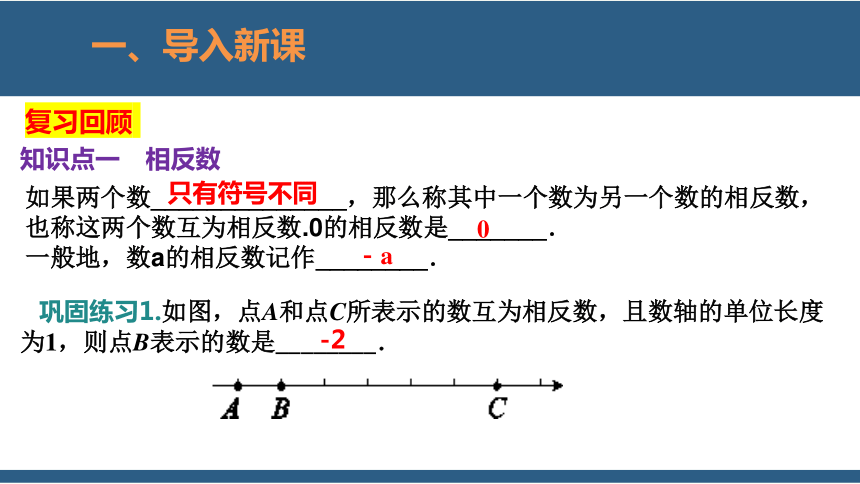
知识点一 相反数
如果两个数______________,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.0的相反数是_______.
一般地,数a的相反数记作________.
只有符号不同
0
-a
复习回顾
巩固练习1.如图,点A和点C所表示的数互为相反数,且数轴的单位长度为1,则点B表示的数是________.
-2
巩固练习2.下列说法正确的是( )A.一个数的绝对值等于它本身,这个数一定是正数B.一个数的绝对值等于它的相反数,这个数一定是负数C.绝对值越大,这个数越大D.两个负数,绝对值大的那个数反而小
一、导入新课
D
知识点二 绝对值
1.在数轴上,一个数所对应的点与原点的_____叫做这个数的绝对值.
2.表示:a的绝对值记作|a|.
3.性质:正数的绝对值是它_______;负数的绝对值是它的______;
0的绝对值是________.
距离
本身
相反数
0
知识点三 利用绝对值比较两个负数的大小
两个负数比较大小,____________________.
绝对值大的反而小
一、导入新课
情境导入
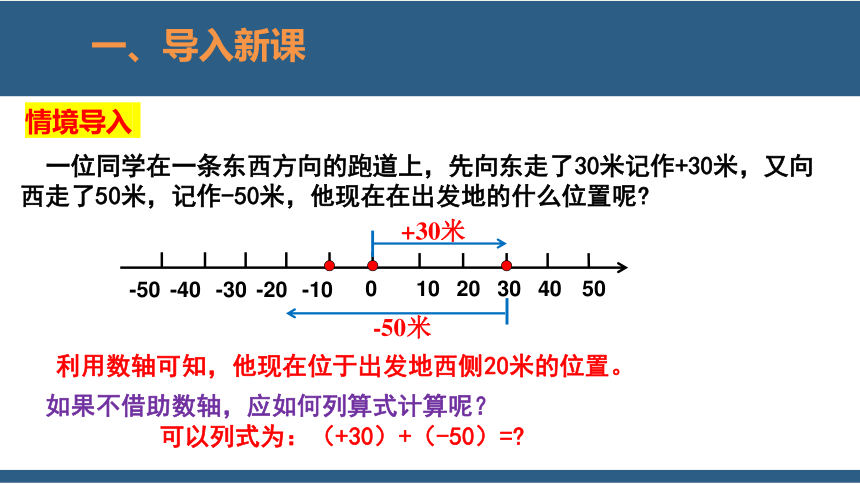
一位同学在一条东西方向的跑道上,先向东走了30米记作+30米,又向西走了50米,记作-50米,他现在在出发地的什么位置呢
0
10
20
30
40
50
-50
-40
-30
-20
-10
+30米
-50米
如果不借助数轴,应如何列算式计算呢?
可以列式为:(+30)+(-50)=
利用数轴可知,他现在位于出发地西侧20米的位置。
二、新知探究
探究一:有理数的加法
答对一题,
答错一题,
得0分.
答错一题,
答对一题,
也得0分.
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分。
答对
答错
不回答
二、新知探究
如果我们用1个 表示+1,用1个 表示-1,那么 就表示0.同样, 也表示0.
+
-
+
-
+
-
你能根据以上方法,计算以下各式吗?
用算式表示为:
(+1)+(-1)=0
(-1)+(+1)=0
二、新知探究
在方框中放进2个 和3个 :
-
-
-
-
-
-
-
-
-
-
-
-
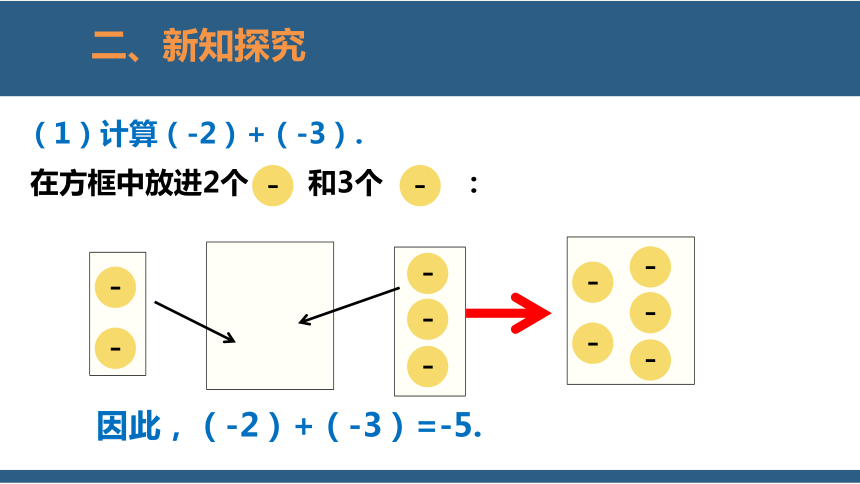
(1)计算(-2)+(-3).
因此,(-2)+(-3)=-5.
二、新知探究
在方框中放进3个 和2个 :
-
+
-
-
-
因此,(-3)+2=-1
-
-
-
+
+
+
+
-
(2)计算(-3)+2.
相互抵消
为0
二、新知探究
(3)你能用类似的方法计算3+(-2),(-4)+4吗?与同伴进行交流。
3+(-2)=1
(-4)+4 =0
1.两个有理数相加,和的符号怎样确定?和的绝对值如何确定?
二、新知探究
( - 2 ) + ( - 3 ) = - ( 2 + 3 )= - 5
↓ ↓ ↓
( - 3 ) + 2 = - ( 3 - 2) = -1
↓ ↓ ↓
议一议
两个加数的绝对 值相加
较大的绝对值减去较小的绝对值
同号两数相加
取相同符号
异号两数相加
取绝对值较大的数的符号
2.一个有理数同0相加,和是多少?
二、新知探究
( + 2 ) + 0 = 2
( - 3 ) + 0 = -3
议一议
一个数同0相加,仍得这个数。
( - 4 ) + 4 = 0
↓ ↓ ↓
和为0
异号两数相加,绝对值相等时
二、新知探究
有理数加法法则
(1)同号两数相加,取相同的符号,并把绝对值相加.
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
(3)一个数同0相加,仍得这个数.
总结归纳
二、新知探究
跟踪练习:(1)180+(-10); (2)(-10)+(-1);
(3) 5+(-5); (4)0+(-2).
解:(1)180+(-10)
=+(180-10)
=170
---------异号两数相加
取绝对值较大数的符号,并用较大的绝对值减去较小的绝对值
------
(2)(-10)+(-1)
=-(10+1)
=-11
---------同号两数相加
--------取相同的符号,并把绝对值相加
(3)5+(-5)
=0
---------互为相反数的两数相加
--------结果为0
(2)0+(-2)
=-2
---------一个数同0相加
--------仍得这个数
二、新知探究
二、新知探究
探究二:有理数加法的应用
某检修小组从A地出发在东西方向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中的行驶记录(单位:千米)如下:-4,+7,-9,+8,
+6,-4,-3.回答下列问题:
(1)收工时在A地的什么位置 距A地多远
(2)若每千米耗油0.3升从出发到收工共耗油多少升
解:(1)(-4)+(+7)+(-9)+(+8)+(+6)+(-4)+(-3)= 1.
答:收工时距A地1 m,且在A地东边。
(2)0.3x(|-4|+|+7|+|-9|+|+8|+|+6|+|-4|+|-3|)=0.3x41=12.3(升).
答:从出发到收工共耗油 12.3 升。
二、新知探究
思考题:用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b 0;
(2)如果a<0,b<0,那么a+b 0;
(3)如果a>0,b<0,|a|>|b|,那么a+b 0;
(4)如果a<0,b>0,|a|>|b|,那么a+b 0.
>
<
>
<
拓展延伸
三、典例精析
例1 计算:
(1)-150+(+15); (2)(-20)+(-11);
(3)(-72)+(+72); (4)(-39)+0;
(5)(+135)+(-75); (6)(-124)+(+176).
解:(1)(-150)+(+15)
=-(150-15)
=-135.
(2)(-20)+(-11)
=-(20+11)
=-31.
三、典例精析
(4)(-39)+0
=-39.
(3)(-72)+(+72)
=0
(5)(+135)+(-75)
=+(135-75)
=60.
(6)(-124)+(+176)
=+(176-124)
=52.
三、典例精析
例2:若A地的海拔高度为-120 m,B地比A地高46 m,则B地的海拔高度是多少?
解:(-120)+46=-(120-46)=-74(m).
因此,B地的海拔高度为-74 m.
四、当堂练习
1.下列各式运算正确的是( )A.(-3)+(+7)=-4 B.(-2)+(+2)=-4C.(+6)+(-11)=-5 D.(-5)+(+3)=-8
2.在数4,-1,3,-6中,任取两个不同的数相加,其中和的最小值是( )
A.3 B.-3 C.-7 D.无法确定
C
C
四、当堂练习
3.若有理数a,b在数轴上对应的点的位置如所示,则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
4.若两个有理数的和为负数,则这两个有理数( )A.一定都是负数 B.一正一负,且负数的绝对值大C.一个为零,另一个为负数 D.至少有一个是负数
A
D
四、当堂练习
5.绝对值大于2而小于5的所有负整数的和是________.
6.月球围绕地球转动时,其反面在被太阳光照亮的情况下,横越过太平洋需数小时.若该天月球横越太平洋前的表面温度为-165 ℃,横越太平洋后,月球的表面温度上升了247 ℃,则横越太平洋后月球的表面温度为________.
-7
82℃
四、当堂练习
7.计算:(1)(-23)+(-32); (2)(-35)+47;
(3)(-55)+55; (4)(+57)+(-102).
解:(1)(-23)+(-32)
=-(23+32)
=-55.
(2)(-35)+47
=+(47-35)
=12.
(3)(-55)+55
=0.
(4)(+57)+(-102)
=-(102-57)
=-45.
五、课堂小结
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
六、作业布置
习题2.4
第1课时
北师大版 数学 七年级上册
4 有理数的加法
第二章 有理数及其运算
学习目标
1.了解有理数加法的意义,理解有理数加法法则的合理性;
2.掌握有理数加法法则,并能运用法则进行计算;(重点)
3.经历探究有理数加法法则的过程,深刻感受分类讨论、数形结合的思想,感受由具体到抽象、由特殊到一般的认知规律。(难点)
一、导入新课
知识点一 相反数
如果两个数______________,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.0的相反数是_______.
一般地,数a的相反数记作________.
只有符号不同
0
-a
复习回顾
巩固练习1.如图,点A和点C所表示的数互为相反数,且数轴的单位长度为1,则点B表示的数是________.
-2
巩固练习2.下列说法正确的是( )A.一个数的绝对值等于它本身,这个数一定是正数B.一个数的绝对值等于它的相反数,这个数一定是负数C.绝对值越大,这个数越大D.两个负数,绝对值大的那个数反而小
一、导入新课
D
知识点二 绝对值
1.在数轴上,一个数所对应的点与原点的_____叫做这个数的绝对值.
2.表示:a的绝对值记作|a|.
3.性质:正数的绝对值是它_______;负数的绝对值是它的______;
0的绝对值是________.
距离
本身
相反数
0
知识点三 利用绝对值比较两个负数的大小
两个负数比较大小,____________________.
绝对值大的反而小
一、导入新课
情境导入
一位同学在一条东西方向的跑道上,先向东走了30米记作+30米,又向西走了50米,记作-50米,他现在在出发地的什么位置呢
0
10
20
30
40
50
-50
-40
-30
-20
-10
+30米
-50米
如果不借助数轴,应如何列算式计算呢?
可以列式为:(+30)+(-50)=
利用数轴可知,他现在位于出发地西侧20米的位置。
二、新知探究
探究一:有理数的加法
答对一题,
答错一题,
得0分.
答错一题,
答对一题,
也得0分.
某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不回答得0分。
答对
答错
不回答
二、新知探究
如果我们用1个 表示+1,用1个 表示-1,那么 就表示0.同样, 也表示0.
+
-
+
-
+
-
你能根据以上方法,计算以下各式吗?
用算式表示为:
(+1)+(-1)=0
(-1)+(+1)=0
二、新知探究
在方框中放进2个 和3个 :
-
-
-
-
-
-
-
-
-
-
-
-
(1)计算(-2)+(-3).
因此,(-2)+(-3)=-5.
二、新知探究
在方框中放进3个 和2个 :
-
+
-
-
-
因此,(-3)+2=-1
-
-
-
+
+
+
+
-
(2)计算(-3)+2.
相互抵消
为0
二、新知探究
(3)你能用类似的方法计算3+(-2),(-4)+4吗?与同伴进行交流。
3+(-2)=1
(-4)+4 =0
1.两个有理数相加,和的符号怎样确定?和的绝对值如何确定?
二、新知探究
( - 2 ) + ( - 3 ) = - ( 2 + 3 )= - 5
↓ ↓ ↓
( - 3 ) + 2 = - ( 3 - 2) = -1
↓ ↓ ↓
议一议
两个加数的绝对 值相加
较大的绝对值减去较小的绝对值
同号两数相加
取相同符号
异号两数相加
取绝对值较大的数的符号
2.一个有理数同0相加,和是多少?
二、新知探究
( + 2 ) + 0 = 2
( - 3 ) + 0 = -3
议一议
一个数同0相加,仍得这个数。
( - 4 ) + 4 = 0
↓ ↓ ↓
和为0
异号两数相加,绝对值相等时
二、新知探究
有理数加法法则
(1)同号两数相加,取相同的符号,并把绝对值相加.
(2)异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.
(3)一个数同0相加,仍得这个数.
总结归纳
二、新知探究
跟踪练习:(1)180+(-10); (2)(-10)+(-1);
(3) 5+(-5); (4)0+(-2).
解:(1)180+(-10)
=+(180-10)
=170
---------异号两数相加
取绝对值较大数的符号,并用较大的绝对值减去较小的绝对值
------
(2)(-10)+(-1)
=-(10+1)
=-11
---------同号两数相加
--------取相同的符号,并把绝对值相加
(3)5+(-5)
=0
---------互为相反数的两数相加
--------结果为0
(2)0+(-2)
=-2
---------一个数同0相加
--------仍得这个数
二、新知探究
二、新知探究
探究二:有理数加法的应用
某检修小组从A地出发在东西方向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中的行驶记录(单位:千米)如下:-4,+7,-9,+8,
+6,-4,-3.回答下列问题:
(1)收工时在A地的什么位置 距A地多远
(2)若每千米耗油0.3升从出发到收工共耗油多少升
解:(1)(-4)+(+7)+(-9)+(+8)+(+6)+(-4)+(-3)= 1.
答:收工时距A地1 m,且在A地东边。
(2)0.3x(|-4|+|+7|+|-9|+|+8|+|+6|+|-4|+|-3|)=0.3x41=12.3(升).
答:从出发到收工共耗油 12.3 升。
二、新知探究
思考题:用“>”或“<”号填空:
(1)如果a>0,b>0,那么a+b 0;
(2)如果a<0,b<0,那么a+b 0;
(3)如果a>0,b<0,|a|>|b|,那么a+b 0;
(4)如果a<0,b>0,|a|>|b|,那么a+b 0.
>
<
>
<
拓展延伸
三、典例精析
例1 计算:
(1)-150+(+15); (2)(-20)+(-11);
(3)(-72)+(+72); (4)(-39)+0;
(5)(+135)+(-75); (6)(-124)+(+176).
解:(1)(-150)+(+15)
=-(150-15)
=-135.
(2)(-20)+(-11)
=-(20+11)
=-31.
三、典例精析
(4)(-39)+0
=-39.
(3)(-72)+(+72)
=0
(5)(+135)+(-75)
=+(135-75)
=60.
(6)(-124)+(+176)
=+(176-124)
=52.
三、典例精析
例2:若A地的海拔高度为-120 m,B地比A地高46 m,则B地的海拔高度是多少?
解:(-120)+46=-(120-46)=-74(m).
因此,B地的海拔高度为-74 m.
四、当堂练习
1.下列各式运算正确的是( )A.(-3)+(+7)=-4 B.(-2)+(+2)=-4C.(+6)+(-11)=-5 D.(-5)+(+3)=-8
2.在数4,-1,3,-6中,任取两个不同的数相加,其中和的最小值是( )
A.3 B.-3 C.-7 D.无法确定
C
C
四、当堂练习
3.若有理数a,b在数轴上对应的点的位置如所示,则a+b的值( )
A.大于0 B.小于0 C.小于a D.大于b
4.若两个有理数的和为负数,则这两个有理数( )A.一定都是负数 B.一正一负,且负数的绝对值大C.一个为零,另一个为负数 D.至少有一个是负数
A
D
四、当堂练习
5.绝对值大于2而小于5的所有负整数的和是________.
6.月球围绕地球转动时,其反面在被太阳光照亮的情况下,横越过太平洋需数小时.若该天月球横越太平洋前的表面温度为-165 ℃,横越太平洋后,月球的表面温度上升了247 ℃,则横越太平洋后月球的表面温度为________.
-7
82℃
四、当堂练习
7.计算:(1)(-23)+(-32); (2)(-35)+47;
(3)(-55)+55; (4)(+57)+(-102).
解:(1)(-23)+(-32)
=-(23+32)
=-55.
(2)(-35)+47
=+(47-35)
=12.
(3)(-55)+55
=0.
(4)(+57)+(-102)
=-(102-57)
=-45.
五、课堂小结
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
六、作业布置
习题2.4
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
