三角形中位线教学课件
图片预览




文档简介
课件16张PPT。三角形的中位线潮南区初二数学优质课评比参评课例
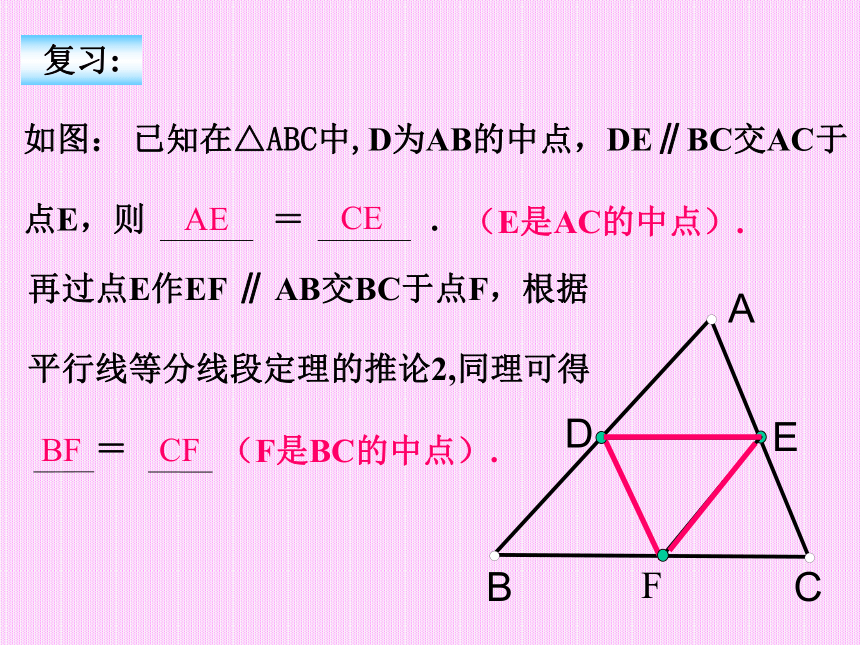
主讲:峡山初级中学 如图: 已知在△ABC中,D为AB的中点,DE∥BC交AC于
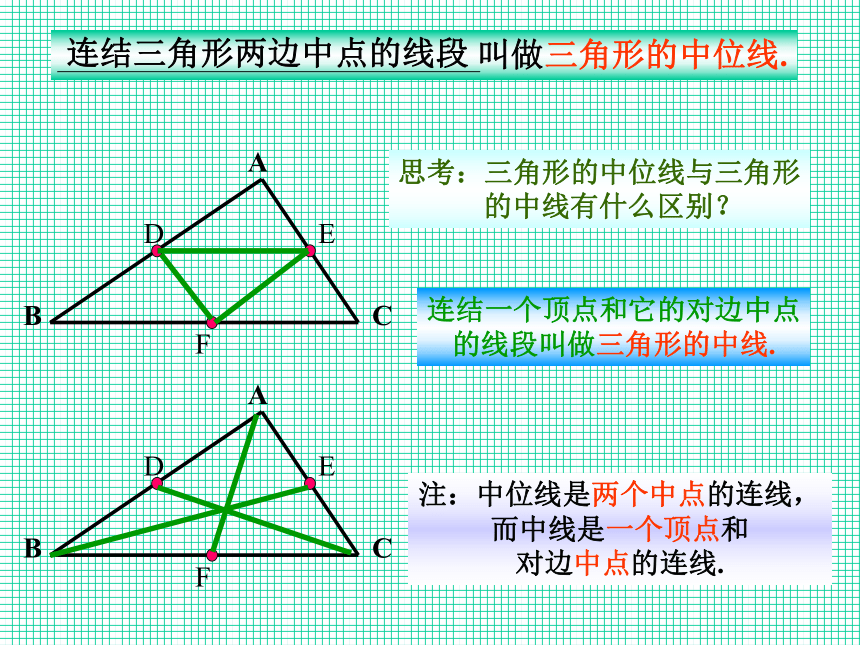
点E,则 = .(E是AC的中点).(F是BC的中点).AECEBFCF复习:思考:三角形的中位线与三角形 的中线有什么区别?注:中位线是两个中点的连线, 而中线是一个顶点和
对边中点的连线.连结一个顶点和它的对边中点
的线段叫做三角形的中线.连结三角形两边中点的线段
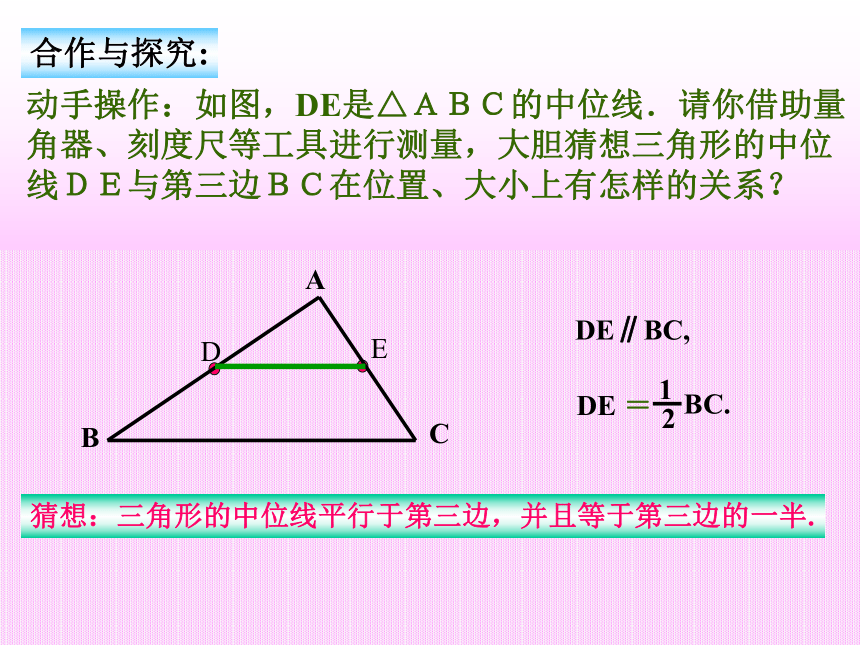
动手操作:如图,DE是△ABC的中位线.请你借助量角器、刻度尺等工具进行测量,大胆猜想三角形的中位线DE与第三边BC在位置、大小上有怎样的关系?
合作与探究:猜想:三角形的中位线平行于第三边,并且等于第三边的一半.求证:三角形的中位线平行于第三边,并且等于 第三边的一半.已知:如图,在△ABC中,D是AB的中点,E是AC的中点.
证明:在△ABC中,D是AB的中点, E是AC的中点.如果过点D作DE '∥BC交AC于E',那么E '是AC的中点(平行线等分线段定理推论2).可见DE与DE '重合,求证:三角形的中位线平行于第三边,并且等于 第三边的一半.已知:如图,在△ABC中,D是AB的中点,E是AC的中点.
求证:DE∥BC,证明:在△ABC中,D是AB的中点, E是AC的中点. DE=BC.如果过点D作DE ' ∥BC交AC于E ' ,那么E '是AC的中点(平行线等分线段定理推论2).可见DE与DE '重合,因此DE∥BC.同样,过点D作DF ∥ AC,交BC于F,则BF=CF.∵四边形DFCE是平行四边形,∴DE=CF.
如图:DE 、EF 、DF都是△ABC的中位线. 三角形的中位线定理:三角形的中位线平行于第 三边,并且等于第三边的一半.
1 .如图:若D、E、F分别是AB、AC、BC的中点,则有
(1)EF∥( ),EF=( )AB,AC∥( ) ,AC=2( ).
(2)若DE=4,则BC=( ).若AC=10,则DF=( ).
(3)若△ABC的AC=6cm、AB=8cm、BC=10cm,
则△DEF的周长为( ).
若△DEF的周长为15cm,
则 △ABC的周长为( ).
2.A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并 分别找出AC和BC的中点M、N.如果测得MN=20cm,那么A、 B两点的距离是多少?为什么?BCAMNAB 巩固练习题: (口答) DF DF8512cm 30cm
求证:顺次连结四边形各边中点,所得的四边形
是平行四边形.
已知:E、F、G、H分别是四边形ABCD
中AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
证明:连结AC.∵ AH=HD,CG=GD.∴ 四边形EFGH是平行四边形.例1:
求证:顺次连结四边形各边中点,所得的四边形
是平行四边形.
已知:E、F、G、H分别是四边形ABCD
中AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
例1: 证明:连结AC、BD.∵ AH=HD,CG=GD.∴ 四边形EFGH是平行四边形.∴ HG =EF, EH = FG菱形.菱形.
求证:顺次连结四边形各边中点,所得的四边形
是平行四边形.
已知:E、F、G、H分别是四边形ABCD
中AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
例1: 证明:连结AC、BD.∵ AH=HD,CG=GD.∴ 四边形EFGH是平行四边形.∴ HG ∥ EF, EH ∥ FG同理 EF∥AC,EH ∥ BD,FG ∥ BD.矩形.
已知:梯形ABCD,AD∥BC,对角线AC、BD相交于点O, A’、B’、C’、D’分别是AO、BO、CO、DO的中点. 求证 :(1)四边形A’B’C’D’是梯形; (2)梯形ABCD的周长等于梯形A’B’C’D’周长的2倍.
ABCDOA’B’C’D’练习:课堂小结:1.三角形中位线的定义:
连结三角形两边中点的线段叫做三角形的中位线.2.三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.书面作业:习题4.7A组第4、6小题(二选一)(1)如图:延长DE至F,
使DE=EF,连结CF(2)如图:过点C作CF ∥AB,交DE
的延长线于点F课后作业:三角形中位线定理的其他证法:再见
主讲:峡山初级中学 如图: 已知在△ABC中,D为AB的中点,DE∥BC交AC于
点E,则 = .(E是AC的中点).(F是BC的中点).AECEBFCF复习:思考:三角形的中位线与三角形 的中线有什么区别?注:中位线是两个中点的连线, 而中线是一个顶点和
对边中点的连线.连结一个顶点和它的对边中点
的线段叫做三角形的中线.连结三角形两边中点的线段
动手操作:如图,DE是△ABC的中位线.请你借助量角器、刻度尺等工具进行测量,大胆猜想三角形的中位线DE与第三边BC在位置、大小上有怎样的关系?
合作与探究:猜想:三角形的中位线平行于第三边,并且等于第三边的一半.求证:三角形的中位线平行于第三边,并且等于 第三边的一半.已知:如图,在△ABC中,D是AB的中点,E是AC的中点.
证明:在△ABC中,D是AB的中点, E是AC的中点.如果过点D作DE '∥BC交AC于E',那么E '是AC的中点(平行线等分线段定理推论2).可见DE与DE '重合,求证:三角形的中位线平行于第三边,并且等于 第三边的一半.已知:如图,在△ABC中,D是AB的中点,E是AC的中点.
求证:DE∥BC,证明:在△ABC中,D是AB的中点, E是AC的中点. DE=BC.如果过点D作DE ' ∥BC交AC于E ' ,那么E '是AC的中点(平行线等分线段定理推论2).可见DE与DE '重合,因此DE∥BC.同样,过点D作DF ∥ AC,交BC于F,则BF=CF.∵四边形DFCE是平行四边形,∴DE=CF.
如图:DE 、EF 、DF都是△ABC的中位线. 三角形的中位线定理:三角形的中位线平行于第 三边,并且等于第三边的一半.
1 .如图:若D、E、F分别是AB、AC、BC的中点,则有
(1)EF∥( ),EF=( )AB,AC∥( ) ,AC=2( ).
(2)若DE=4,则BC=( ).若AC=10,则DF=( ).
(3)若△ABC的AC=6cm、AB=8cm、BC=10cm,
则△DEF的周长为( ).
若△DEF的周长为15cm,
则 △ABC的周长为( ).
2.A、B两点被池塘隔开,在AB外选一点C,连结AC和BC,并 分别找出AC和BC的中点M、N.如果测得MN=20cm,那么A、 B两点的距离是多少?为什么?BCAMNAB 巩固练习题: (口答) DF DF8512cm 30cm
求证:顺次连结四边形各边中点,所得的四边形
是平行四边形.
已知:E、F、G、H分别是四边形ABCD
中AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
证明:连结AC.∵ AH=HD,CG=GD.∴ 四边形EFGH是平行四边形.例1:
求证:顺次连结四边形各边中点,所得的四边形
是平行四边形.
已知:E、F、G、H分别是四边形ABCD
中AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
例1: 证明:连结AC、BD.∵ AH=HD,CG=GD.∴ 四边形EFGH是平行四边形.∴ HG =EF, EH = FG菱形.菱形.
求证:顺次连结四边形各边中点,所得的四边形
是平行四边形.
已知:E、F、G、H分别是四边形ABCD
中AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
例1: 证明:连结AC、BD.∵ AH=HD,CG=GD.∴ 四边形EFGH是平行四边形.∴ HG ∥ EF, EH ∥ FG同理 EF∥AC,EH ∥ BD,FG ∥ BD.矩形.
已知:梯形ABCD,AD∥BC,对角线AC、BD相交于点O, A’、B’、C’、D’分别是AO、BO、CO、DO的中点. 求证 :(1)四边形A’B’C’D’是梯形; (2)梯形ABCD的周长等于梯形A’B’C’D’周长的2倍.
ABCDOA’B’C’D’练习:课堂小结:1.三角形中位线的定义:
连结三角形两边中点的线段叫做三角形的中位线.2.三角形的中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.书面作业:习题4.7A组第4、6小题(二选一)(1)如图:延长DE至F,
使DE=EF,连结CF(2)如图:过点C作CF ∥AB,交DE
的延长线于点F课后作业:三角形中位线定理的其他证法:再见
