25.2 用列举法求概率 第2课时(树状图) 课件(共16张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 25.2 用列举法求概率 第2课时(树状图) 课件(共16张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 452.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 20:13:38 | ||
图片预览




文档简介
(共16张PPT)
画树状图法求概率
25.2 用列举法求概率
|25.2 用列举法求概率 第2课时|
知识回顾
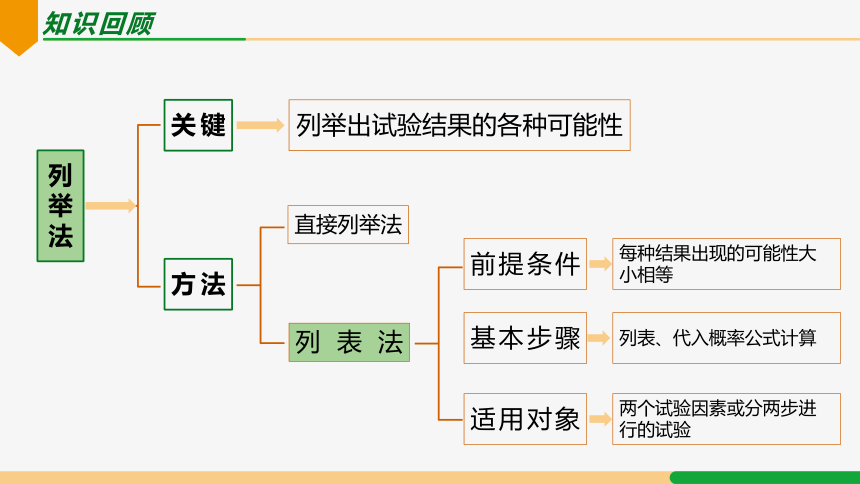
列举法
关键
方法
列举出试验结果的各种可能性
直接列举法
列表法
前提条件
适用对象
基本步骤
每种结果出现的可能性大小相等
列表、代入概率公式计算
两个试验因素或分两步进行的试验
新知探究
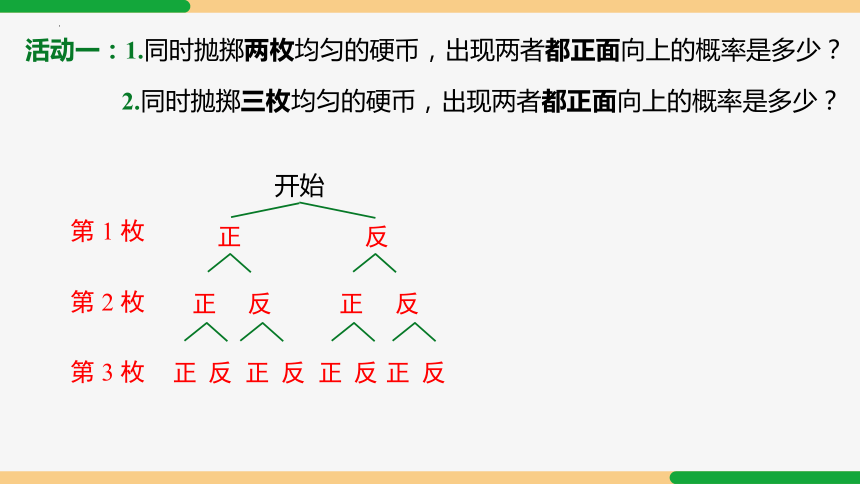
活动一:1.同时抛掷两枚均匀的硬币,出现两者都正面向上的概率是多少?
第1枚
第2枚
结
果
正
反
正
反
解:列表可得
2.同时抛掷三枚均匀的硬币,出现两者都正面向上的概率是多少?
第 2 枚
正
反
反
开始
正
反
第 1 枚
正
2.同时抛掷三枚均匀的硬币,出现两者都正面向上的概率是多少?
活动一:1.同时抛掷两枚均匀的硬币,出现两者都正面向上的概率是多少?
第 3 枚
正
正
正
正
反
反
反
反
知识要点1
树状图法
1、将第一步可能出现的 a 种等可能的结果写在第一层;
2、 若第二步有 b 种等可能的结果,则在第一层的每个结果下画出 b 个分支,将这 b 种结果写在第二层,以此类推,画出第三层;
3、根据树状图求出所关注事件包含的1结果数及所有等可能的结果数,再利用概率公式求解。
典例讲解
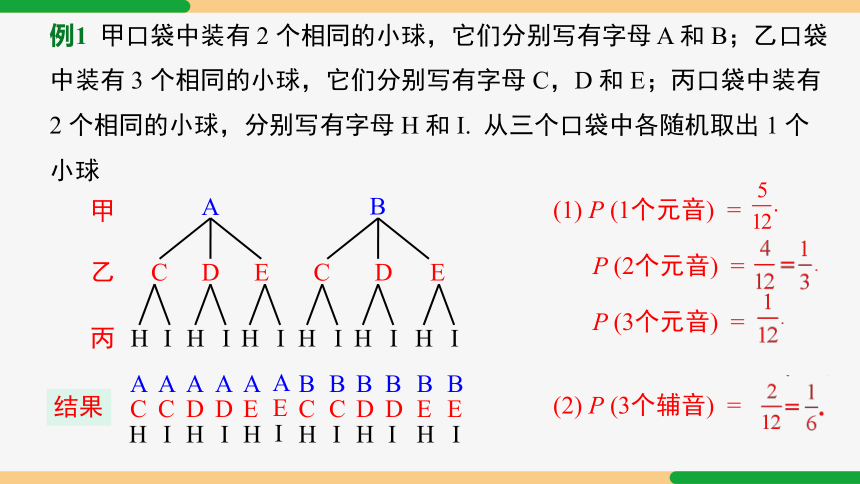
例1 甲口袋中装有 2 个相同的小球,它们分别写有字母 A 和 B;乙口袋中装有 3 个相同的小球,它们分别写有字母 C,D 和 E;丙口袋中装有 2 个相同的小球,分别写有字母 H 和 I. 从三个口袋中各随机取出 1 个小球.
(1) 取出的 3 个小球上恰好有 1 个,2 个,3 个有元音字母的概率分别是多少?
(2) 取出的 3 个小球上全是辅音字母的概率是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
结果
例1 甲口袋中装有 2 个相同的小球,它们分别写有字母 A 和 B;乙口袋中装有 3 个相同的小球,它们分别写有字母 C,D 和 E;丙口袋中装有 2 个相同的小球,分别写有字母 H 和 I. 从三个口袋中各随机取出 1 个小球
(1) P (1个元音) =
P (2个元音) =
P (3个元音) =
(2) P (3个辅音) =
例2 小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的 3 个红球和 2 个黑球,两人先后从袋中取出一个球(不放回) ,若两人所取球的颜色相同,则小明胜;否则,小军胜;
(1) 请用树状图或列表法求出摸球游戏所有可能的结果;
(2) 你觉得本游戏规则是否公平,请说明理由.
(1) 解:先将三个红球分别记为“红1”“红2”“红3”“黑1”“黑2”,然后画树状图如下:
红1
红3
小军
小明
红2
开始
黑1
黑2
红2
红3
黑1
黑2
红1
红3
黑1
黑2
红1
红2
黑1
黑2
红2
红3
红1
黑2
红2
红3
红1
黑1
(2) 解:不公平.
∵由树状图可知共有 20 种等可能的结果,
∴两人所取球的颜色相同有 8 种结果,则
∴这个游戏不公平.
红1 红2 红3 黑1 黑2
红1 红2红1 红3红1 黑1红1 黑2红1
红2 红1红2 红3红2 黑1红2 黑2红2
红3 红1红3 红2红3 黑1红3 黑2红3
黑1 红1黑1 红2黑1 红3黑1 黑2黑1
黑2 红1黑2 红2黑2 红3黑2 黑1黑2
方法二:列表如下
小军
小明
结
果
课堂小结
树状图
步骤
注意
1.关键要弄清楚每一步有几种结果;
2.在树状图下面对应写着所有可能的结果,并找出事件所包含的结果数;
3.利用概率公式进行计算.
1.弄清试验涉及试验因素个数或试验步骤分几步;
2.在摸球试验一定要弄清“放回”还是“不放回”.
课堂练习
2. a、b、c、d 四本不同的书放入一个书包,至少放一本,最多放两本,共有 种不同的放法.
1. 三女一男四人同行,从中任意选出两人,其性别不同的概率为( )
10
C
经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是__________
学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是____________
在一个不透明的袋子里,装有三个分别写有数字 7,6,-2 的小球,它们的形状、大小、质地等完全相同. 先从袋子里随机取出一个小球,记下数字后放回袋子里,摇匀后再随机取出一个小球,记下数字. 请你用列表或画树状图的方法求下列事件的概率.
(1) 两次取出的小球上的数字相同;
(2) 两次取出的小球上的数字之和大于 10.
6
-2
7
(1) 两次取出的小球上的数字相同的可能性只有 3 种,
所以 P(数字相同) =
(2) 两次取出的小球上的数字之和大于 10 可能性只有 4 种,所以 P(数字之和大于 10) =
解:根据题意,画出树状图如下:
第一个数字
第二个数字
6
6
-2
7
-2
6
-2
7
7
6
-2
7
画树状图法求概率
25.2 用列举法求概率
|25.2 用列举法求概率 第2课时|
知识回顾
列举法
关键
方法
列举出试验结果的各种可能性
直接列举法
列表法
前提条件
适用对象
基本步骤
每种结果出现的可能性大小相等
列表、代入概率公式计算
两个试验因素或分两步进行的试验
新知探究
活动一:1.同时抛掷两枚均匀的硬币,出现两者都正面向上的概率是多少?
第1枚
第2枚
结
果
正
反
正
反
解:列表可得
2.同时抛掷三枚均匀的硬币,出现两者都正面向上的概率是多少?
第 2 枚
正
反
反
开始
正
反
第 1 枚
正
2.同时抛掷三枚均匀的硬币,出现两者都正面向上的概率是多少?
活动一:1.同时抛掷两枚均匀的硬币,出现两者都正面向上的概率是多少?
第 3 枚
正
正
正
正
反
反
反
反
知识要点1
树状图法
1、将第一步可能出现的 a 种等可能的结果写在第一层;
2、 若第二步有 b 种等可能的结果,则在第一层的每个结果下画出 b 个分支,将这 b 种结果写在第二层,以此类推,画出第三层;
3、根据树状图求出所关注事件包含的1结果数及所有等可能的结果数,再利用概率公式求解。
典例讲解
例1 甲口袋中装有 2 个相同的小球,它们分别写有字母 A 和 B;乙口袋中装有 3 个相同的小球,它们分别写有字母 C,D 和 E;丙口袋中装有 2 个相同的小球,分别写有字母 H 和 I. 从三个口袋中各随机取出 1 个小球.
(1) 取出的 3 个小球上恰好有 1 个,2 个,3 个有元音字母的概率分别是多少?
(2) 取出的 3 个小球上全是辅音字母的概率是多少?
甲
乙
丙
A
C
D
E
H
I
H
I
H
I
B
C
D
E
H
I
H
I
H
I
B
C
H
A
C
H
A
C
I
A
D
H
A
D
I
A
E
H
A
E
I
B
C
I
B
D
H
B
D
I
B
E
H
B
E
I
结果
例1 甲口袋中装有 2 个相同的小球,它们分别写有字母 A 和 B;乙口袋中装有 3 个相同的小球,它们分别写有字母 C,D 和 E;丙口袋中装有 2 个相同的小球,分别写有字母 H 和 I. 从三个口袋中各随机取出 1 个小球
(1) P (1个元音) =
P (2个元音) =
P (3个元音) =
(2) P (3个辅音) =
例2 小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的 3 个红球和 2 个黑球,两人先后从袋中取出一个球(不放回) ,若两人所取球的颜色相同,则小明胜;否则,小军胜;
(1) 请用树状图或列表法求出摸球游戏所有可能的结果;
(2) 你觉得本游戏规则是否公平,请说明理由.
(1) 解:先将三个红球分别记为“红1”“红2”“红3”“黑1”“黑2”,然后画树状图如下:
红1
红3
小军
小明
红2
开始
黑1
黑2
红2
红3
黑1
黑2
红1
红3
黑1
黑2
红1
红2
黑1
黑2
红2
红3
红1
黑2
红2
红3
红1
黑1
(2) 解:不公平.
∵由树状图可知共有 20 种等可能的结果,
∴两人所取球的颜色相同有 8 种结果,则
∴这个游戏不公平.
红1 红2 红3 黑1 黑2
红1 红2红1 红3红1 黑1红1 黑2红1
红2 红1红2 红3红2 黑1红2 黑2红2
红3 红1红3 红2红3 黑1红3 黑2红3
黑1 红1黑1 红2黑1 红3黑1 黑2黑1
黑2 红1黑2 红2黑2 红3黑2 黑1黑2
方法二:列表如下
小军
小明
结
果
课堂小结
树状图
步骤
注意
1.关键要弄清楚每一步有几种结果;
2.在树状图下面对应写着所有可能的结果,并找出事件所包含的结果数;
3.利用概率公式进行计算.
1.弄清试验涉及试验因素个数或试验步骤分几步;
2.在摸球试验一定要弄清“放回”还是“不放回”.
课堂练习
2. a、b、c、d 四本不同的书放入一个书包,至少放一本,最多放两本,共有 种不同的放法.
1. 三女一男四人同行,从中任意选出两人,其性别不同的概率为( )
10
C
经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,则两辆汽车经过这个十字路口时,一辆向右转,一辆向左转的概率是__________
学校组织校外实践活动,安排给九年级三辆车,小明与小红都可以从这三辆车中任选一辆搭乘,小明与小红同车的概率是____________
在一个不透明的袋子里,装有三个分别写有数字 7,6,-2 的小球,它们的形状、大小、质地等完全相同. 先从袋子里随机取出一个小球,记下数字后放回袋子里,摇匀后再随机取出一个小球,记下数字. 请你用列表或画树状图的方法求下列事件的概率.
(1) 两次取出的小球上的数字相同;
(2) 两次取出的小球上的数字之和大于 10.
6
-2
7
(1) 两次取出的小球上的数字相同的可能性只有 3 种,
所以 P(数字相同) =
(2) 两次取出的小球上的数字之和大于 10 可能性只有 4 种,所以 P(数字之和大于 10) =
解:根据题意,画出树状图如下:
第一个数字
第二个数字
6
6
-2
7
-2
6
-2
7
7
6
-2
7
同课章节目录
