第25章 概率初步小结与复习 第1课时(知识小结) 课件(共31张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版)
文档属性
| 名称 | 第25章 概率初步小结与复习 第1课时(知识小结) 课件(共31张PPT)-2023-2024学年九年级数学上册随堂教学课件(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 00:00:00 | ||
图片预览






文档简介
知识小结
第25章 概率初步
| 第25章 小结与复习 第1课时|
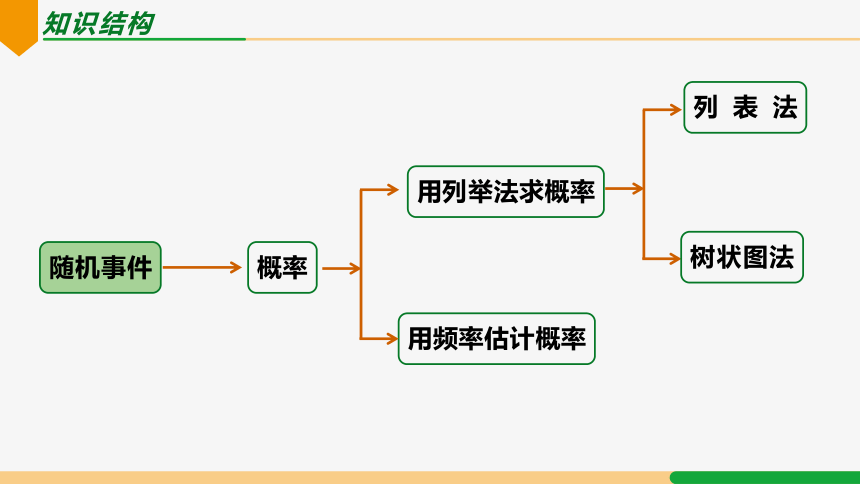
知识结构
随机事件
用列举法求概率
概率
用频率估计概率
列表法
树状图法
知识回顾
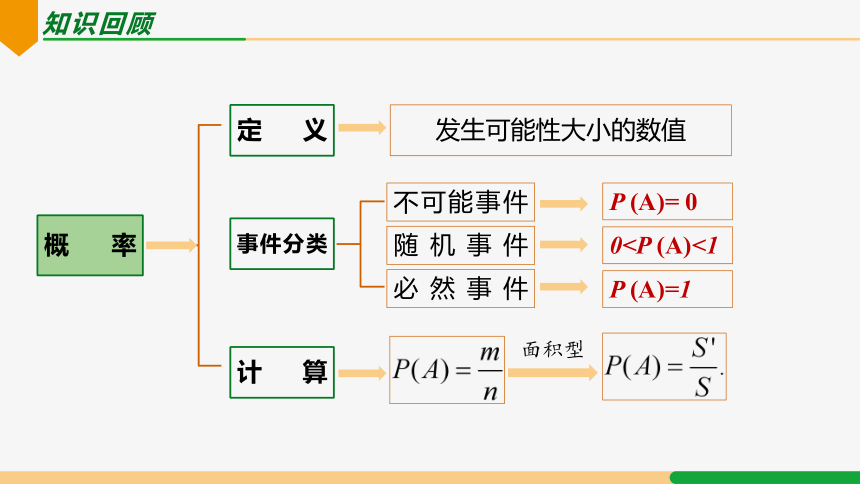
概率
定义
事件分类
计算
发生可能性大小的数值
不可能事件
必然事件
随机事件
P (A)= 0
0
P (A)=1
面积型
知识要点
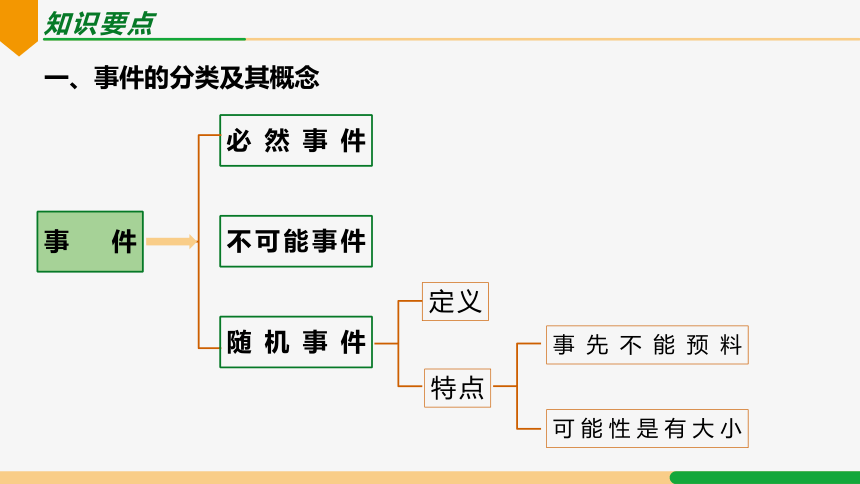
事件
必然事件
不可能事件
随机事件
定义
特点
事先不能预料
可能性是有大小
一、事件的分类及其概念
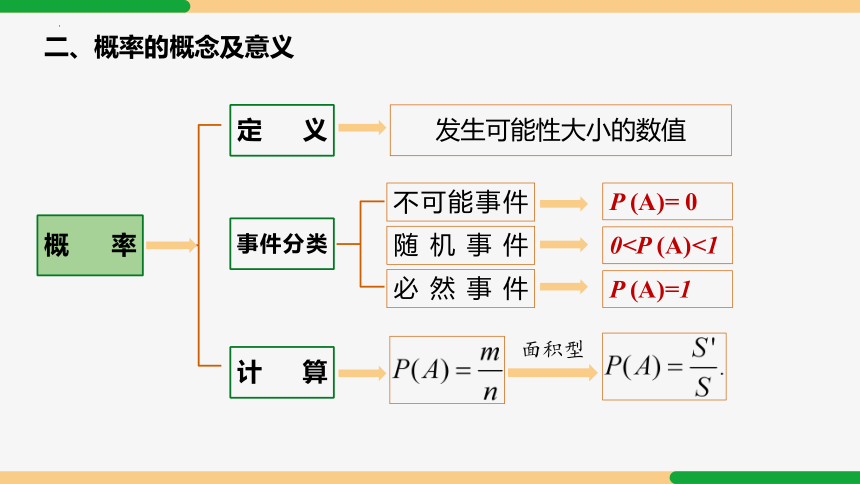
概率
定义
事件分类
计算
发生可能性大小的数值
不可能事件
必然事件
随机事件
P (A)= 0
0
P (A)=1
面积型
二、概率的概念及意义
三、随机事件的概率的求法
求随机事件概率的方法
列表法:适合于两个试验因素或分两步进行
树状图:适合于三个及以上试验因素或分三步进行
直接列举法
四、用频率估计概率
用频率估计概率
一般地,在大量重复试验中,如果事件 A 发生的频率 稳定于某个常数 p,那么事件 A 发生的概率:P(A) = p
典例讲解
考点一 事件的判断和概率的意义
例1 (江苏联考)下列事件中,随机事件是( )
A. 在标准大气压下,温度低于 0 ℃ 时水结冰
B. 小明到达公共汽车站时,1 路公交车正在驶来
C. 同时抛掷两枚质地均匀的骰子,向上一面的点数之和为 13
D. 在同一年出生的 14 名学生中,至少有 2 人出生在同一个月
B
考点二 概率的计算
例2 (1) 一个口袋中装有 3 个红球,2 个绿球,1 个黄球,每个球除颜色外其他都相同,搅匀后随机地从中摸出一个球是绿球的概率是______.
(2) 三张分别画有平行四边形、等边三角形、圆的卡片,它们的背面都相同,现将它们背面朝上,从中任取一张,卡片上所画图形恰好是中心对称图形的概率是______.
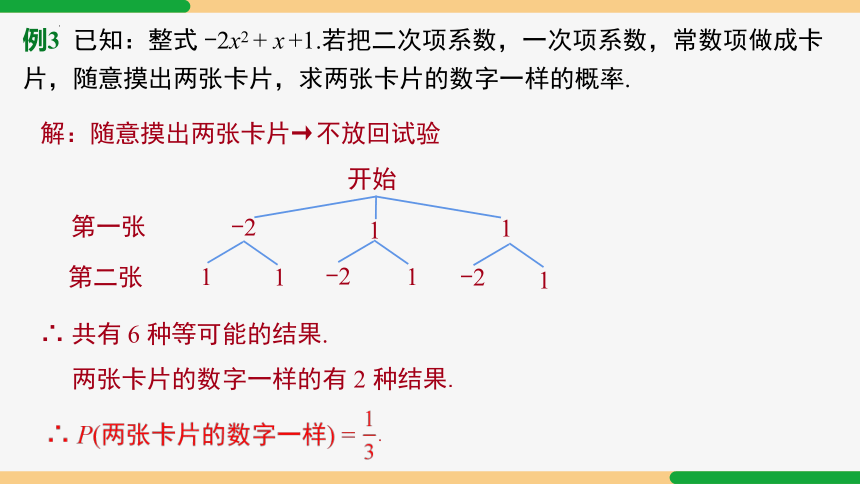
例3 已知:整式 -2x2 + x +1.若把二次项系数,一次项系数,常数项做成卡片,随意摸出两张卡片,求两张卡片的数字一样的概率.
解:随意摸出两张卡片→不放回试验
第二张
第一张
-2
1
1
1
开始
1
-2
1
-2
1
∴ 共有 6 种等可能的结果.
两张卡片的数字一样的有 2 种结果.
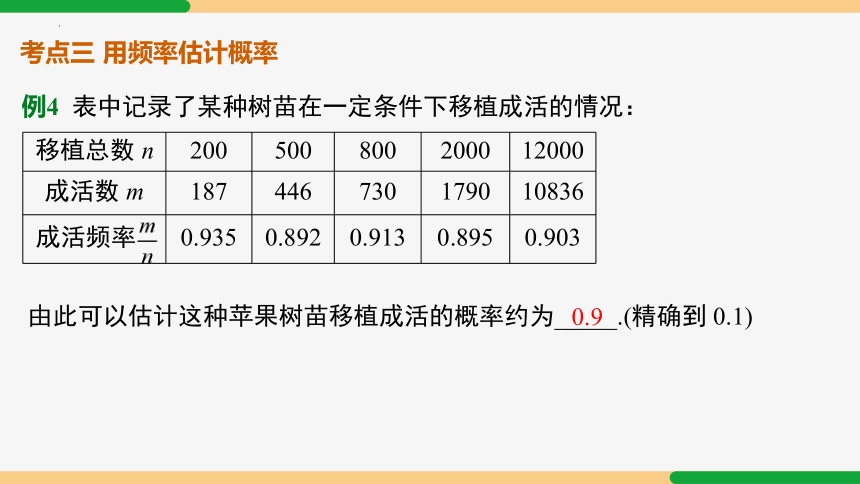
考点三 用频率估计概率
例4 表中记录了某种树苗在一定条件下移植成活的情况:
移植总数 n 200 500 800 2000 12000
成活数 m 187 446 730 1790 10836
成活频率 0.935 0.892 0.913 0.895 0.903
由此可以估计这种苹果树苗移植成活的概率约为_____.(精确到 0.1)
0.9
考点四 用概率作决策
例5 在一个不透明的口袋里装有分别标注 2、4、6 的 3 个小球(小球除数字外,其余都相同),另有 3 张背面完全一样,正面分别写有数字 6、7、8 的卡片.现从口袋中任意摸出一个小球,再从这 3 张背面朝上的卡片中任意摸出一张卡片.
(1) 请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2) 小红和小莉做游戏,制定了两个游戏规则:
规则 1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢;
规则 2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢. 小红想要在游戏中获胜,她会选择哪一条规则?说明理由.
解:(1) 列表如下:
2 4 6
6 (2,6) (4,6) (6,6)
7 (2,7) (4,7) (6,7)
8 (2,8) (4,8) (6,8)
小球
卡片
共有 9 种等可能结果.
解: 规则 1:P (小红赢) = ;
规则 2:P (小红赢) = .
∵ ,∴ 小红会选择规则 1.
课堂练习
1.“闭上眼睛从布袋中随机地摸出 1 个球,恰是红球的概率是 ”的意思是 ( )
A.布袋中有 2 个红球和 5 个其他颜色的球
B.如果摸球次数很多,那么平均每摸 7 次,就有 2 次摸中红球
C.摸 7 次,就有 2 次摸中红球
D.摸 7 次,就有 5 次摸不中红球
B
小明把如图所示的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域的概率是_______
一个不透明的袋中装有分别标有 -2, -1,3,4 四个数字且大小形状完全相同的四个小球,随机摸出一个小球记下数字,然后放回搅匀,再从中摸出一个小球记下数字,两次的数字分别记为 b,c. 则方程 x2 + bx + c = 0 有两个不相等的实数根的概率是______.
解:画树状图的如下:
-2
3
c
b
-1
开始
4
-2
-1
3
4
-2
-1
3
4
-2
-1
3
4
-2
-1
3
4
由树状图可知,共有 16 种等可能的结果,
其中方程 x2 + bx + c = 0 有两个不相等的实数根(b2 - 4c>0)的情况有 9 种,
∴ 方程 x2 + bx + c = 0 有两个不相等的概率是
不透明的袋子中装有红球、黄球、蓝球各一个,这些球除颜色外无其他差别.
(1) 从袋子中随机摸出一个球,摸到蓝球的概率是___.
(2) 从袋子中随机摸出一个球后,放回并摇匀,再随机摸出一个球,请用列表或者树状图的方法,求两次摸到的球的颜色为“一红一黄”的概率.
解:(1) 不透明的袋子中共有 3 个球,其中 1 个蓝球,
∴ 随机摸出一个球,摸到蓝球的概率是
(2) 根据题意列表如下:
红 黄 蓝
红 红红 黄红 蓝红
黄 红黄 黄黄 蓝黄
蓝 红蓝 黄蓝 蓝蓝
由表可知,共有 9 种等
可能的情况数,
其中摸到“一红一黄”的情况有 2 种,则两次摸到的球的颜色为“一红一黄”的概率是
一个不透明的口袋中有红球和黑球共 25 个,这些球除颜色外都相同. 进行大量的摸球试验(每次摸出 1 个球)后,发现摸到黑球的频率在 0.6 附近摆动,据此可以估计黑球为________个.
15
在一个不透明的袋子中装有 3 个白球和若干个红球,这些球除颜色外都相同. 每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在 0.7 附近,则袋子中红球约有_______个.
解析:设袋中红球有 x 个,
由题意可知 , 解得 x = 7.
经检验:x = 7 是分式方程的解. 所以袋中红球有 7 个.
7
A、B 两个小型超市举行有奖促销活动,顾客每购满 20 元就有一次按下面规则转动转盘获奖机会,且两超市奖额等同. 规则是:
① A 超市把转盘甲等分成 4 个扇形区域、B 超市把转盘乙等分成 3 个扇形区域,并标上了数字 (如图所示);
② 顾客第一回转动转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).
1
1
2
2
3
3
4
甲
乙
解:A、B 两超市顾客转盘获奖的事件记为 M、N.
1 2 3 4
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
第一回
第二回
甲转盘
共有 16 种结果,其中中奖的有 8 种,
(1) 利用树状图或列表法分别求出 A、B 两超市顾客一 回转盘获奖的概率;
1 2 3
1 2 3 4
2 3 4 5
3 4 5 6
第一回
第二回
乙转盘
共有 9 种等可能结果,其中中奖的有 4 种,
(2) 如果只考虑中奖因素,你将会选择去哪个超市购物?说明理由.
解:选 A 超市.理由如下:
∵ P (M) > P(N),
∴ 选 A 超市.
下列事件为确定事件的有( )
(1)打开电视正在播动画片 (2)长、宽为,的矩形面积是mn,(3)掷一枚质地均匀的硬币,正面朝上(4)是无理数
A.个 B.个 C.个 D.个
【详解】打开电视正在播动画片,是随机事件,不合题意;
长、宽为m,n的矩形面积是mn,是确定事件,符合题意;
掷一枚质地均匀的硬币,正面朝上,是随机事件,不合题意;
是无理数,是确定事件,符合题意;
故选:B.
某校九年级选出三名同学参加学校组织的“法治和安全知识竞赛”.比赛规定,以抽签方式决定每个人的出场顺序,主持人将表示出场顺序的数字1,2,3分别写在3张同样的纸条上,并将这些纸条放在一个不透明的盒子中,搅匀后从中任意抽出一张,小星第一个抽,下列说法中正确的是( )
A.小星抽到数字1的可能性最小 B.小星抽到数字2的可能性最大
C.小星抽到数字3的可能性最大 D.小星抽到每个数的可能性相同
D
在一个不透明的布袋内,有红球5个,黄球4个,白球1个,蓝球3个,它们除颜色外,大小、质地都相同.若随机从袋中摸取一个球,则摸中哪种球的概率最大( )
A.红球 B.黄球 C.白球 D.蓝球
在一个不透明的布袋内,有红球5个,黄球4个,白球1个,蓝球3个,它们除颜色外,大小、质地都相同.若随机从袋中摸取一个球,因为红球的个数最多,所以摸到红球的概率最大,摸到红球的概率是: 故选:A
A
如图,是由个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )
A. B. C. D.
解:先设每个小等边三角的面积为,
则阴影部分的面积是,整个图形的面积是,
则这个点取在阴影部分的概率是.
故选:D.
D
将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为( )
A. B. C. D.
解:如图,
根据题意得:图中每个小三角形的面积都相等,
设每个小三角形的面积为a,则阴影的面积为6a,正六边形的面积为18a,
∴将一枚飞镖任意投掷到镖盘上,飞镖落在阴影区域的概率为=.
故选:B
B
【详解】解:把“5G时代”、“北斗卫星”、“高铁速度”三个主题分别记为A、B、C,画树状图如下:
共有9种等可能的结果,其中小明和小刚恰好选择同一个主题的结果有3种,
∴小明和小刚恰好选择同一个主题的概率为.
故选:C.
某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )
A. B. C. D.
C
如图,两个相同的可以自由转动的转盘A和B,转盘A被三等分,分别标有数字2,0,-1;转盘B被四等分,分别标有数字3,2,-2,-3.如果同时转动转盘A,B,转盘停止时,两个指针指向转盘A,B上的对应数字分别为x,y(当指针指在两个扇形的交线时,需重新转动转盘),那么点落在直角坐标系第二象限的概率是______________.
由表可知,共有12种等可能,
其中点落在直角坐标系第二象限的有2种,
所以点落在直角坐标系第二象限的概率是,
故答案为:.
在一个不透明的袋子里装有红球、黄球共个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在左右,则袋子中红球的个数最有可能是( )
A. B. C. D.
【详解】解:设袋子中红球有x个,
根据题意,得:
解得x=5
答:袋子中红球有5个.
故选:A.
A
