14.1 勾股定理(第1课时)(教学课件)28张ppt
文档属性
| 名称 | 14.1 勾股定理(第1课时)(教学课件)28张ppt |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 10:51:02 | ||
图片预览








文档简介
14.1 勾股定理
第1课时 直角三角形三边关系
数学(华东师大版)
八年级 上册
第14章 勾股定理
学习目标
1、掌握勾股定理及其简单应用,理解定理的一般探究方法;
2、通过利用方格纸计算面积的方法探索勾股定理,经历观察、归纳、猜想和验证的数学发现过程,发展数形结合的数学思想;
导入新课
你知道2002年在北京召开的国际数学家大会(ICM-2002)吗?在这次大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
导入新课
1955年希腊发行的一枚纪念邮票.
这张邮票是纪念二千五百年前希腊的一个学派和宗教团体──毕达哥拉斯学派.
邮票上的图案是根据一个著名的数学定理设计的.
观察这枚邮票上的图案,数数图案中各正方形中小方格的个数,你有什么猜想?
讲授新课
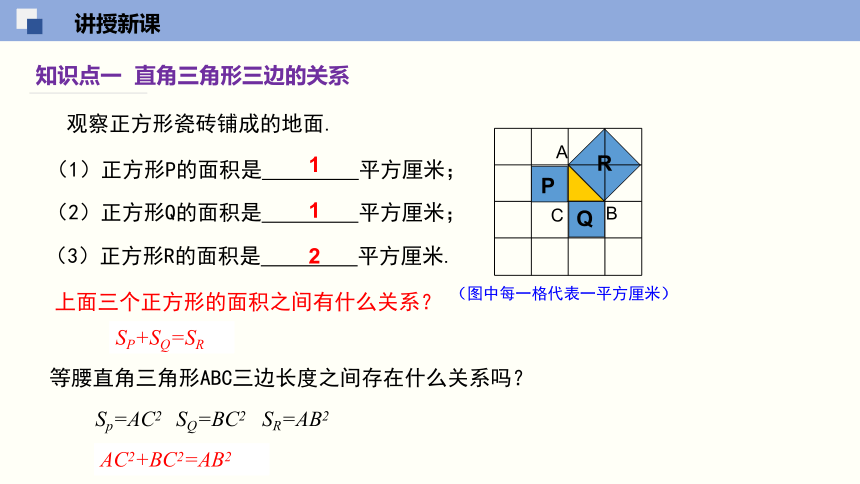
知识点一 直角三角形三边的关系
(图中每一格代表一平方厘米)
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
观察正方形瓷砖铺成的地面.
讲授新课
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
想一想
讲授新课
填一填.
观察右边两幅图:完成下表(每个小正方形的面积为单位1).
A的面积
B的面积
C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
讲授新课
直角三角形三边关系的证明方法:
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
讲授新课
分析表中数据,你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系?
A
B
C
a
c
b
a2+b2=c2
讲授新课
由上面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2,
a
b
c
这种关系我们称为勾股定理.
即 直角三角形两直角边的平方和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
概念总结
讲授新课
思考:怎样证明勾股定理?
左图是弦图的示意图,它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.
大正方形的面积=c2.
四个全等的直角三角形和小正方形的面积之和= .
即a2+b2=c2.
讲授新课
做
一
做
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,也能证明勾股定理.请你试一试,写出完整的证明过程.
讲授新课
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积之和= .
由题可知(a+b)2=2ab+c2,
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
讲授新课
典例精析
【例1】求出下列直角三角形中未知边的长度.
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
x2 =100
x2=62+82
∵x>0,
y2+52=132
y2=132-52
y2=144
∴ y=12.
(2)在Rt△ABC中,由勾股定理得:
AC2+BC2=AB2
∵y>0,
A
6
8
x
C
B
5
y
13
C
A
B
∴ x=10.
(1)
(2)
讲授新课
练一练
(1)在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=________;
(2)在Rt△ABC中,∠C=90°,AB=25,AC=20,则BC=________;
(3)在Rt△ABC中,∠C=90°,它的两边是6和8,则它的第三边长是________.
13
15
10或
讲授新课
2.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
讲授新课
3.如图,以Rt△ABC的三条边为直径的半圆的面积分别为S1、S2、S3,已知S1=9,S3=25,求S2.
解:由图形可得
S1=????????π(????????????)2=????????????????????,
S2=????????π(????????????)2=????????????????????,
S3=????????π(????????????)2=????????????????????,
AB2+AC2=BC2,∴S1+S2=????????(AC2+AB2)=????????BC2=S3 .
∴S2=S3-S1=25-9=16.
?
讲授新课
勾股图中的面积关系:
以直角三角形的三边为基础,分别向外作半圆、正方形、等边三角形,如图,它们都形成了简单的勾股图. 对于这些勾股图,它们都具有相同的结论,即S3=S1+S2. 与直角三角形三边相连的图形还可以换成正五边形、正六边形等,结论同样成立.
当堂检测
1.求下列图中未知数x、y、z的值.
x=15
y=5
z=7
81
16
x
y
144
169
z
625
576
当堂检测
2. 如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
C
B
A
当堂检测
3.如图,正方形中的数据表示它的面积,则第三个正方形的面积为( )
A.69 B.18 C.19 D.20
C
25
44
A
B
C
当堂检测
4.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.
(1)若c=15,b=12,求a的长;
(2)若a=11,b=60,求c的长;
(3)若a∶b=3∶4,c=10,求a、b的长.
解:(1)∵a2+b2=c2,
∴a2=c2-b2=152-122=81.
∴a=9.
(2)∵a2+b2=c2,
∴c2=112+602=3721.
∴c=61.
(3)∵a∶b=3∶4,
∴设a=3x,b=4x(x>0).
∵a2+b2=c2,
∴(3x)2+(4x)2=102,
整理,得25x2=100,
∴x2=4.
∴x=2.
∴a=3x=6,b=4x=8.
当堂检测
5.如图,在△ABC中,AB=AC,BM=CM,AB=13cm,BC=24 cm.求△ABC的面积.
B
A
C
M
解:∵AB=AC,BM=CM,
∴AM⊥BC,即∠AMB=90°.
在△ABM中,∠AMB=90°,AB=13 cm,
BM=CM=????????BC=12 cm,
根据勾股定理,得
AM2=AB2-BM2=132-122=25.
∴AM=5 cm.
∴S△ABC=????????BC·AM=????????×24×5=60(cm2).
?
当堂检测
6.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
解:S大正方形=5×5=25,
所以S四边形ABCD=25-12.5=12.5.
四个直角三角形的面积之和=1×2×
+2×4× +3×3× +2×3× =12.5
当堂检测
6.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
C四边形ABCD=AD+DC+BC+AB
答:四边形ABCD的面积是12.5,周长约是14.6.
课堂小结
勾股定理
定理
验证
1.求边长、面积,证明线段之间的平方关系
2.勾股定理的实际应用
应用
直角三角形两直角边的平方和等于斜边的平方
用拼图法验证勾股定理
谢 谢~
第1课时 直角三角形三边关系
数学(华东师大版)
八年级 上册
第14章 勾股定理
学习目标
1、掌握勾股定理及其简单应用,理解定理的一般探究方法;
2、通过利用方格纸计算面积的方法探索勾股定理,经历观察、归纳、猜想和验证的数学发现过程,发展数形结合的数学思想;
导入新课
你知道2002年在北京召开的国际数学家大会(ICM-2002)吗?在这次大会上,到处可以看到一个简洁优美、远看像旋转的纸风车的图案,它就是大会的会标.
会标采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
导入新课
1955年希腊发行的一枚纪念邮票.
这张邮票是纪念二千五百年前希腊的一个学派和宗教团体──毕达哥拉斯学派.
邮票上的图案是根据一个著名的数学定理设计的.
观察这枚邮票上的图案,数数图案中各正方形中小方格的个数,你有什么猜想?
讲授新课
知识点一 直角三角形三边的关系
(图中每一格代表一平方厘米)
(1)正方形P的面积是 平方厘米;
(2)正方形Q的面积是 平方厘米;
(3)正方形R的面积是 平方厘米.
1
2
1
SP+SQ=SR
R
Q
P
A
C
B
AC2+BC2=AB2
等腰直角三角形ABC三边长度之间存在什么关系吗?
Sp=AC2 SQ=BC2 SR=AB2
上面三个正方形的面积之间有什么关系?
观察正方形瓷砖铺成的地面.
讲授新课
这说明在等腰直角三角形ABC中,两直角边的平方和等于斜边的平方
那么,在一般的直角三角形中,两直角边的平方和是否等于斜边的平方呢?
想一想
讲授新课
填一填.
观察右边两幅图:完成下表(每个小正方形的面积为单位1).
A的面积
B的面积
C的面积
左图
右图
4
?
怎样计算正方形C的面积呢?
9
16
9
讲授新课
直角三角形三边关系的证明方法:
方法一:割
方法二:补
方法三:拼
分割为四个直角三角形和一个小正方形.
补成大正方形,用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形,图中两块红色(或绿色)可拼成一个小正方形.
讲授新课
分析表中数据,你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系?
A
B
C
a
c
b
a2+b2=c2
讲授新课
由上面的探索可以发现:对于任意的直角三角形,如果它的两条直角边分别为a、b,斜边为c,那么一定有
a2+b2=c2,
a
b
c
这种关系我们称为勾股定理.
即 直角三角形两直角边的平方和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
概念总结
讲授新课
思考:怎样证明勾股定理?
左图是弦图的示意图,它由4个全等的直角三角形与一个小正方形组成,恰好拼成一个大正方形.
大正方形的面积=c2.
四个全等的直角三角形和小正方形的面积之和= .
即a2+b2=c2.
讲授新课
做
一
做
用四个全等的直角三角形,还可以拼成如图所示的图形.与上面的方法类似,根据这一图形,也能证明勾股定理.请你试一试,写出完整的证明过程.
讲授新课
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积之和= .
由题可知(a+b)2=2ab+c2,
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
讲授新课
典例精析
【例1】求出下列直角三角形中未知边的长度.
解:(1)在Rt△ABC中,由勾股定理得:AB2=AC2+BC2
x2 =100
x2=62+82
∵x>0,
y2+52=132
y2=132-52
y2=144
∴ y=12.
(2)在Rt△ABC中,由勾股定理得:
AC2+BC2=AB2
∵y>0,
A
6
8
x
C
B
5
y
13
C
A
B
∴ x=10.
(1)
(2)
讲授新课
练一练
(1)在Rt△ABC中,∠C=90°,AC=5,BC=12,则AB=________;
(2)在Rt△ABC中,∠C=90°,AB=25,AC=20,则BC=________;
(3)在Rt△ABC中,∠C=90°,它的两边是6和8,则它的第三边长是________.
13
15
10或
讲授新课
2.若一个直角三角形的两直角边的长分别为a,b,斜边长为c,则下列关于a,b,c的关系式中不正确的是( )
A.b2=c2-a2 B.a2=c2-b2
C.b2=a2-c2 D.c2=a2+b2
C
讲授新课
3.如图,以Rt△ABC的三条边为直径的半圆的面积分别为S1、S2、S3,已知S1=9,S3=25,求S2.
解:由图形可得
S1=????????π(????????????)2=????????????????????,
S2=????????π(????????????)2=????????????????????,
S3=????????π(????????????)2=????????????????????,
AB2+AC2=BC2,∴S1+S2=????????(AC2+AB2)=????????BC2=S3 .
∴S2=S3-S1=25-9=16.
?
讲授新课
勾股图中的面积关系:
以直角三角形的三边为基础,分别向外作半圆、正方形、等边三角形,如图,它们都形成了简单的勾股图. 对于这些勾股图,它们都具有相同的结论,即S3=S1+S2. 与直角三角形三边相连的图形还可以换成正五边形、正六边形等,结论同样成立.
当堂检测
1.求下列图中未知数x、y、z的值.
x=15
y=5
z=7
81
16
x
y
144
169
z
625
576
当堂检测
2. 如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为 ( )
A.3 米 B.4 米 C.5米 D.6米
C
3
4
C
B
A
当堂检测
3.如图,正方形中的数据表示它的面积,则第三个正方形的面积为( )
A.69 B.18 C.19 D.20
C
25
44
A
B
C
当堂检测
4.在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c.
(1)若c=15,b=12,求a的长;
(2)若a=11,b=60,求c的长;
(3)若a∶b=3∶4,c=10,求a、b的长.
解:(1)∵a2+b2=c2,
∴a2=c2-b2=152-122=81.
∴a=9.
(2)∵a2+b2=c2,
∴c2=112+602=3721.
∴c=61.
(3)∵a∶b=3∶4,
∴设a=3x,b=4x(x>0).
∵a2+b2=c2,
∴(3x)2+(4x)2=102,
整理,得25x2=100,
∴x2=4.
∴x=2.
∴a=3x=6,b=4x=8.
当堂检测
5.如图,在△ABC中,AB=AC,BM=CM,AB=13cm,BC=24 cm.求△ABC的面积.
B
A
C
M
解:∵AB=AC,BM=CM,
∴AM⊥BC,即∠AMB=90°.
在△ABM中,∠AMB=90°,AB=13 cm,
BM=CM=????????BC=12 cm,
根据勾股定理,得
AM2=AB2-BM2=132-122=25.
∴AM=5 cm.
∴S△ABC=????????BC·AM=????????×24×5=60(cm2).
?
当堂检测
6.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
解:S大正方形=5×5=25,
所以S四边形ABCD=25-12.5=12.5.
四个直角三角形的面积之和=1×2×
+2×4× +3×3× +2×3× =12.5
当堂检测
6.如图,小方格都是边长为1的正方形.求四边形ABCD的面积与周长. (精确到0.1)
C四边形ABCD=AD+DC+BC+AB
答:四边形ABCD的面积是12.5,周长约是14.6.
课堂小结
勾股定理
定理
验证
1.求边长、面积,证明线段之间的平方关系
2.勾股定理的实际应用
应用
直角三角形两直角边的平方和等于斜边的平方
用拼图法验证勾股定理
谢 谢~
