6.4 统计图的选择(第一课时) 课件(共44张PPT)
文档属性
| 名称 | 6.4 统计图的选择(第一课时) 课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-15 12:13:43 | ||
图片预览





文档简介
(共44张PPT)
新课标 北师大版 七年级上册
2023-2024学年度上学期北师大版精品课件
第六章 数据的收集与整理
6.4统计图的选择(第一课时)
学习目标
了解不同统计图的特点,能根据实际问题选择合适的统计图;
能从统计图中获取有效信息,正确决策.
17年
13年
12年
26年
25年
30亿
40亿
50亿
60亿
80亿
90亿
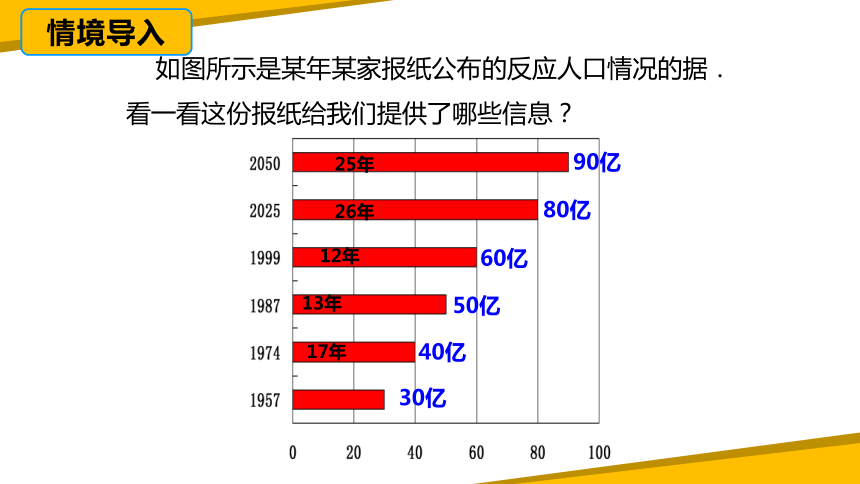
如图所示是某年某家报纸公布的反应人口情况的据.看一看这份报纸给我们提供了哪些信息?
情境导入
选择适当的统计图表示数据
一
探索新知
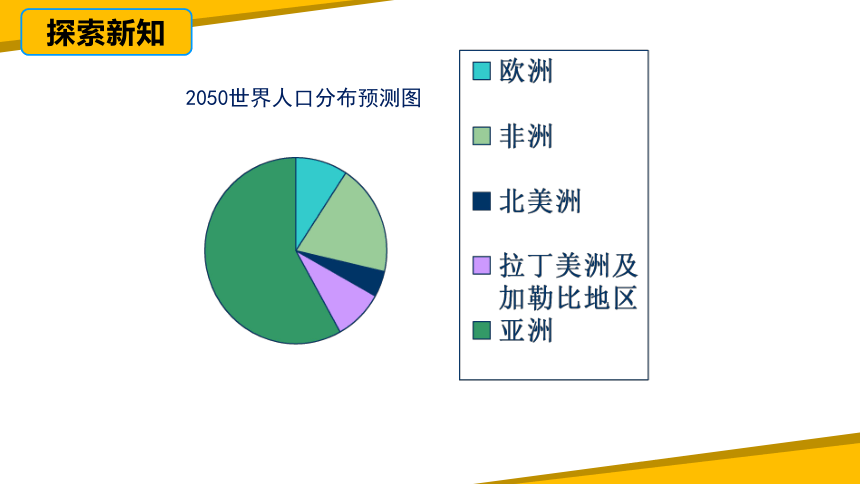
2050世界人口分布预测图
探索新知
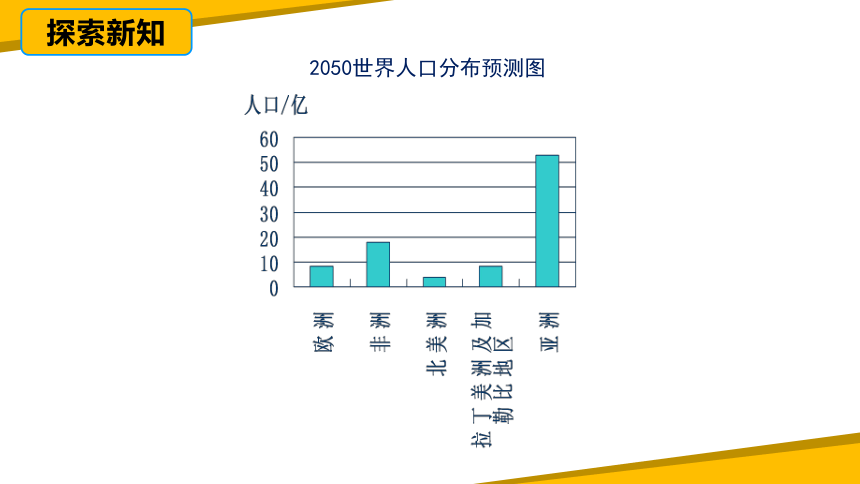
2050世界人口分布预测图
探索新知
根据上图,回答下列问题:
(1)三幅统计图分别表示了什么内容?
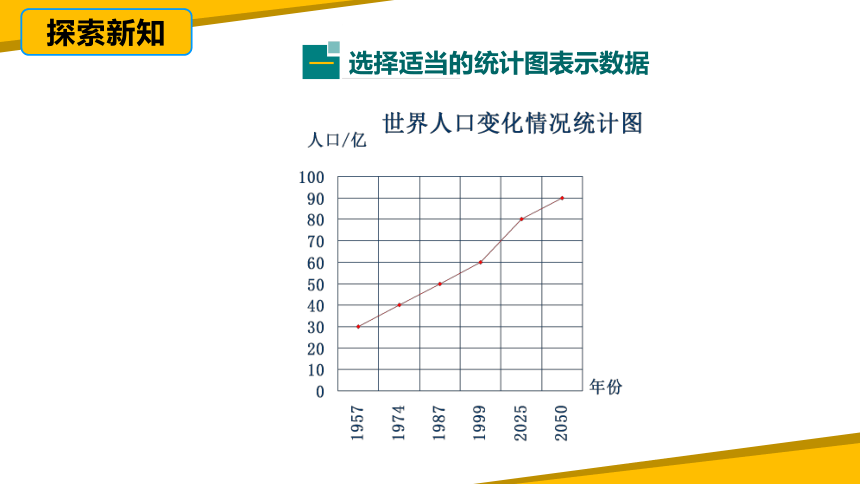
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流.
探索新知
总结归纳
条形统计图能清晰地表示出每个项目的具体数目及它们之间的大小关系.
折线统计图能够清晰地反映同一事物在不同时期的变化情况.
扇形统计图能清晰地表示各部分在总体中所占的百分比及之间的大小关系.
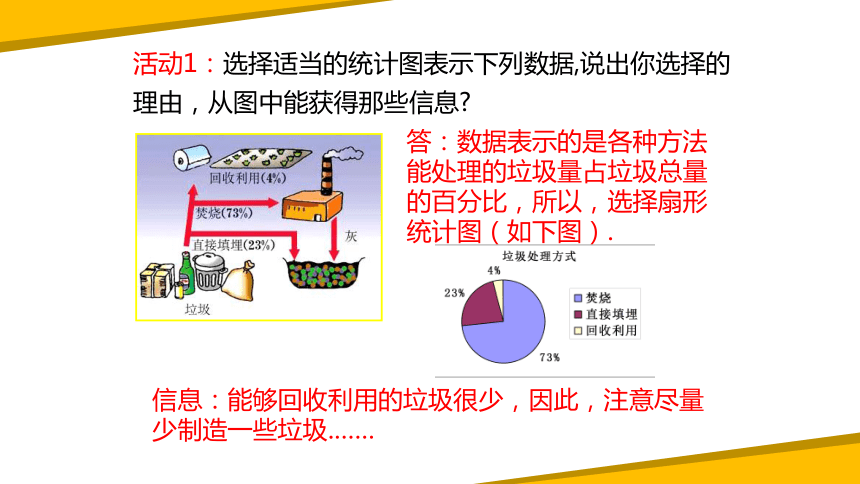
活动1:选择适当的统计图表示下列数据,说出你选择的理由,从图中能获得那些信息
答:数据表示的是各种方法能处理的垃圾量占垃圾总量的百分比,所以,选择扇形统计图(如下图).
信息:能够回收利用的垃圾很少,因此,注意尽量少制造一些垃圾.……
活动2:制作适当的统计图表示下列数据:
答:数据是具体的数量,并且各部分是相互独立的,所以用条形统计图(如下图).
孵化期统计表
探索新知
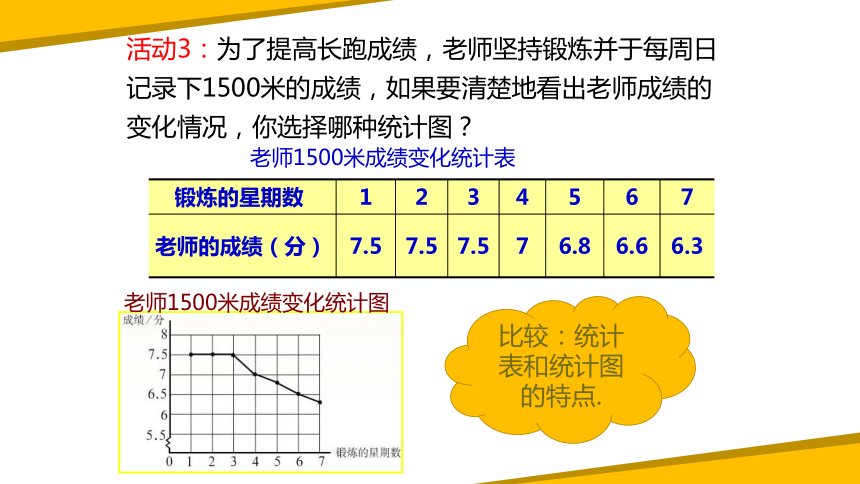
活动3:为了提高长跑成绩,老师坚持锻炼并于每周日记录下1500米的成绩,如果要清楚地看出老师成绩的变化情况,你选择哪种统计图?
锻炼的星期数 1 2 3 4 5 6 7
老师的成绩(分) 7.5 7.5 7.5 7 6.8 6.6 6.3
老师1500米成绩变化统计图
老师1500米成绩变化统计表
比较:统计表和统计图的特点.
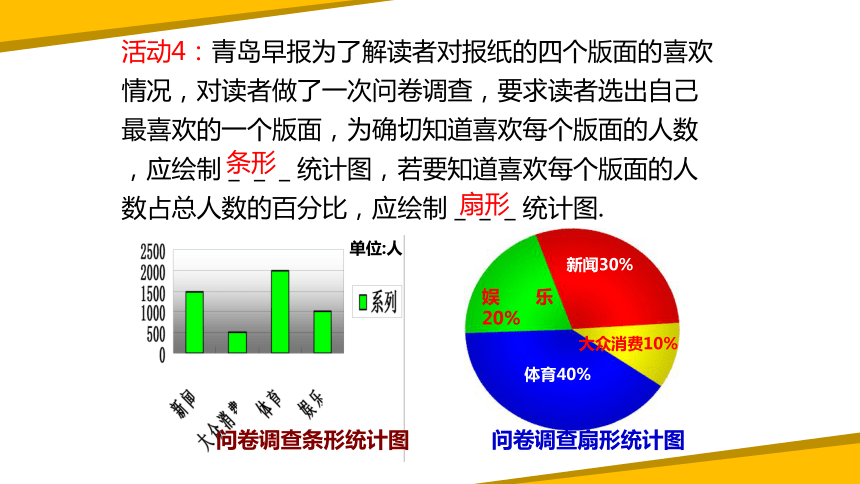
活动4:青岛早报为了解读者对报纸的四个版面的喜欢情况,对读者做了一次问卷调查,要求读者选出自己最喜欢的一个版面,为确切知道喜欢每个版面的人数,应绘制___统计图,若要知道喜欢每个版面的人数占总人数的百分比,应绘制___统计图.
单位:人
问卷调查条形统计图
新闻30%
大众消费10%
体育40%
娱乐20%
问卷调查扇形统计图
条形
扇形
活动5:某气象小组的同学们记录了他们开学后每个月的降水量,得到的数据如下表所示:
月份 九 十 十一 十二
降水量 (mm) 205 150 150 52
请你选择适当的统计图表示这些数据.
统计图的绘制可以不唯一,这个问题,折线统计图和条形统计图都可以,我们应该学会从多个角度来分析数据.
在统计图的选择时,我们应根据三种统计图各自的特点,数据本身的特点,研究问题的需要,来选择适当的统计图.
你能谈谈应该怎样合理选择这三种统计图吗?
议一议
例1 某家电卖场对其销售的空调情况进行了调查,得到了下面的信息:
请你制作适当的统计图,反映下列信息:
例题讲解
解:(1)如图所示.
2012 2013 2014 年份
2 1.5
1.0
0.5
0
销量/万台
2012-2014年,C品牌空调的销售量
(1)2012-2014年,C品牌空调在该卖场销售量的
变化情况;
解:(2)如图所示.
(2)2014年,A,B,C及其他品牌的空调在该卖场的市场
占有率情况.
利用统计图准确表示事物的某个特征
二
甲、乙两种酒近几年的销售量和价格如下:
2002年 2006年 2010年
年度销售量/万瓶 150 180 210
该年度的单价/元 40 50 60
甲品牌酒的产量和价格
2002年 2006年 2010年
年度销售量/万瓶 160 180 200
该年度的单价 40 50 60
乙品牌酒的产量和价格
探究新知
(1)你认为哪一种酒的价格增长较快?为什么?这与上面画出的折线统计图给你的感觉一致吗?为什么图象会给人这样的感觉?
有人根据上面的统计表,制作出甲、乙两种酒的价格变化的折线统计图:
(2)甲种酒的销售人员将甲种酒的销售信息制作成了如下的条形统计图.请你也在右面的图中作出乙种酒的年度销售量的条形统计图:
(3)两幅条形统计图给你的感觉一样吗? 在甲种酒销售人员画的条形统计图中,2010年甲种酒的年度销售量看上去是2002年的多少倍?实际上呢?
(1)为了较直观地比较某两个统计量的变化速度,绘制折线统计图应注意什么?
(2)为了较直观地反映几个统计量之间的比例关系绘制条形统计图时,应注意什么?
在绘制条形统计图时,纵坐标上的起始值应从“0”开始,从而避免造成“误导”、引起“错觉”.
小结
绘制两幅折线统计图,在比较两个统计量的变化趋势时,应注意横(纵)坐标的一致性.
议一议
例2 小明将他的8次数学测验成绩按顺序绘成了如图所示的两幅统计图.
(1)图①和图②给人造成的感觉各是什么?
(2)若小明想向他的父母说明他数学成绩的提高情况,他将向父母展示哪一个统计图?为什么?
例题讲解
解:(1)图①给人的感觉是小明的进步较大,而图②给人的感觉比较平稳,说明小明的进步不是很大.
(2)若小明想向他的父母说明他的数学成绩的提高情况,他将向父母展示图①,因为图①反映小明数学成绩的提高比较明显.
两个统计图中的数学成绩是一样的!
小明绘制了我国2014年和2015年大、中、小学学生人数的扇形统计图,如图(1)(2).根据这个图你能断定我国2015年的大学生人数比2014年多吗?
解:由于不知道这两年的总人数,故不能断定.
[解析] 扇形统计图只能显示各部分在总体中所占的百分比,不同图中的相同对象无法直接比较大小.
做一做
1.七年级七个班开展“学雷锋做好人好事”活动,为了清楚表明三月份各班做好人好事的件数是多少,最好选用( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.都不对
2.某地要反映出2009-2014年降水量的变化情况,应绘制( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.以上都对
B
B
随堂练习
3.如图所示是2010年-2014年期间甲、乙两个公司产品销售情况统计图.由统计图可知,销量增速较快的公司是( )
A.甲公司 B.乙公司
C.一样快 D.无法确定
C
4.某中学七年级(1)班共有学生40人,该班开设了排球、篮球和足球三项体育兴趣课,要求每个学生必须参加,且只能参加其中一项球类运动,图①是该班学生报名后,小明同学经统计而绘制成的条形统计图的一部分.
(1)请你帮小明同学把条形统计图补充完整;
(2)请你根据条形统计图中的数据,改用扇形统计图表示出来(如图②);
解:(1)参加排球兴趣课的有:40-20-12=8(人),如图所示.
(2)从条形统计图可知,参加足球兴趣课的有20人,占总人数的百分比为20÷40×100%=50%,所在扇形圆心角的度数为360°×50%=180°;参加排球兴趣课的有8人,占总人数的百分比为8÷40×100%=20%,所在扇形圆心角的度数为360°×20%=72°;参加篮球兴趣课的有12人,占总人数的百分比为12÷40×100%=30%,所在扇形圆心角的度数为360°×30%=108°,扇形统计图如图②.
足球50%
排球50%
篮球30%
统计图的选择
统计图的选择
统计图引起的错觉
条形统计图注意事项
扇形统计图引起的错觉
折线统计图注意事项
三种统计图的特点
合理选择统计图表示数据
课堂小结
中考链接
1. (2022·广西)空气由多种气体混合而成,为了直观介绍空气中各成分的百分比,最适合使用的统计图是( )
A.条形图 B.折线图 C. 扇形图 D.直方图
2. (2020·牡丹江)在反映某种股票的涨跌情况时,选择( )
A.条形统计图 B. 折线统计图 C.扇形统计图 D.直方图
C
B
当堂测试
1.为研究某种饮料中各成分的百分比,最适合选用的统计图是( )
A.条形统计图 B.图折线统计图
C.扇形统计 D.频数分布直方图
2.要反应一周气温的变化情况,宜采用( )
A.统计表 B. 条形统计图 C. 扇形统计图 D.折线统计图
C
D
当堂测试
4. 在空气的成分中,氮气约占78%,氧气约占21%,其他微量气体约占1%,若要表示以上信息,最合适的统计图是 .
3.要反映我市上周每天的最高气温的变化趋势,最适合采用下列哪种统计图来进行描述( )
A. 条形统计图 B.扇形统计图 C.折线统计图 D.直方图
C
扇形统计图
当堂测试
5.某医院病房护士对一位病人每小时测一次体温,要把这位病人一昼夜体温变化情况用统计图表示出来选用 统计图比较合适(填“条形”、“扇形”、“折线”)
折线
6. 某初中2013年至2022年这十年间入学人数如下表:
当堂测试
根据表格内容,解决下列问题:
(1)若要反映该初中这十年入学人数的变化趋势,最适合的统计图是 .
A.条形统计图
B.扇形统计图
C.折线统计图
(2)与上年相比,该初中入学人数增加最多的年份是 年;
(3)假定每年学生入学后没有转入转出的情况,到2021年底,该初中在校教师总数与在校的三个年级学生总数的比是1:13.如果到2022年底该比值仍不低于1:13,那么2022年该初中在校教师人数至少增加多少?
2022
C
当堂测试
(3)496+517+521=1534(人)1534÷13=118(人)设教师人数增加了x人
解得
答:教师人数至少增加4人.
分层作业
1. 需要清楚地表示每个项目的具体数目应选择( )
A. 折线统计图 B. 扇形统计图
C. 条形统计图 D.以上三者均可
,
【基础达标作业】
2. 下列统计图能够显示数据变化趋势的是( )
A.条形统计图 B. 折线统计图
C.扇形统计图 D.上述统计图都可以
B
C
分层作业
3.下表是我市5月1日-7日最高气温的记录表:
如果要更直观反映我市一周每天的最高气温的变化趋势,你认为应该采用( )
A. 折线统计图 B. 条形统计图
C.频数分布直方图 D.扇形统计图
A
分层作业
【能力提升作业】
4.常见的统计图有条形图、折线图、扇形图、直方图,其中能够显示数据的变化趋势的统计图是 .
5.要表示一个家庭一年用于“教育、服装、食品、其他”这四项的支出各占家庭本年总支出的百分比,最适合采用 统计图.(填“扇形”、“折线”或“条形”)
扇形
折线图
分层作业
【拓展延伸作业】
6. 某校抽查了八(1)班20名学生,测量了他们在800m赛跑后1min的脉搏次数,结果如下(单位:次):144,150,156,165,171,149,162,160,135,159,150,164,168,153,158,139,161,157,154,147.
(1)填写表格
(2)每分钟脉搏次数在150 ≤ x<160这一组的频率是 .(3)若要知道抽测中以上每种范围的人数占总人数的百分比,应选择哪一种统计图?画出你所选择的统计图,并在图中标明相应数据.
解:(1)根据题意,填写表格如下:
(2)每分钟脉搏次数在150 ≤ x<160这一组的频率是 =0.4;
故答案为:0.4
(3)若要知道抽测中以上每种范围的人数占总人数的百分比,应选择扇形统计图,每分钟脉搏次数在130 ≤ x<140这一组的百分比为 ×100%=10%;
每分钟脉博次数在140 ≤ x<150这一组的百分比为 ×100%=15%;
每分钟脉搏次数在150 ≤ x<160这一组的百分比为 ×100%=40%;
每分钟脉搏次数在160 ≤ x<170这一组的百分比为 ×100%=30%;
每分钟脉搏次数在x>170这一组的百分比为 ×100%=5%;
画出扇形统计图,如下:
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 北师大版 七年级上册
2023-2024学年度上学期北师大版精品课件
第六章 数据的收集与整理
6.4统计图的选择(第一课时)
学习目标
了解不同统计图的特点,能根据实际问题选择合适的统计图;
能从统计图中获取有效信息,正确决策.
17年
13年
12年
26年
25年
30亿
40亿
50亿
60亿
80亿
90亿
如图所示是某年某家报纸公布的反应人口情况的据.看一看这份报纸给我们提供了哪些信息?
情境导入
选择适当的统计图表示数据
一
探索新知
2050世界人口分布预测图
探索新知
2050世界人口分布预测图
探索新知
根据上图,回答下列问题:
(1)三幅统计图分别表示了什么内容?
(2)从哪幅统计图中你能看出世界人口的变化情况?
(3)2050年非洲人口大约将达到多少亿?你是从哪幅图中得到这个数据的?
(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅图中可以明显地得到这个结论?
(5)比较三种统计图的特点,并与同伴进行交流.
探索新知
总结归纳
条形统计图能清晰地表示出每个项目的具体数目及它们之间的大小关系.
折线统计图能够清晰地反映同一事物在不同时期的变化情况.
扇形统计图能清晰地表示各部分在总体中所占的百分比及之间的大小关系.
活动1:选择适当的统计图表示下列数据,说出你选择的理由,从图中能获得那些信息
答:数据表示的是各种方法能处理的垃圾量占垃圾总量的百分比,所以,选择扇形统计图(如下图).
信息:能够回收利用的垃圾很少,因此,注意尽量少制造一些垃圾.……
活动2:制作适当的统计图表示下列数据:
答:数据是具体的数量,并且各部分是相互独立的,所以用条形统计图(如下图).
孵化期统计表
探索新知
活动3:为了提高长跑成绩,老师坚持锻炼并于每周日记录下1500米的成绩,如果要清楚地看出老师成绩的变化情况,你选择哪种统计图?
锻炼的星期数 1 2 3 4 5 6 7
老师的成绩(分) 7.5 7.5 7.5 7 6.8 6.6 6.3
老师1500米成绩变化统计图
老师1500米成绩变化统计表
比较:统计表和统计图的特点.
活动4:青岛早报为了解读者对报纸的四个版面的喜欢情况,对读者做了一次问卷调查,要求读者选出自己最喜欢的一个版面,为确切知道喜欢每个版面的人数,应绘制___统计图,若要知道喜欢每个版面的人数占总人数的百分比,应绘制___统计图.
单位:人
问卷调查条形统计图
新闻30%
大众消费10%
体育40%
娱乐20%
问卷调查扇形统计图
条形
扇形
活动5:某气象小组的同学们记录了他们开学后每个月的降水量,得到的数据如下表所示:
月份 九 十 十一 十二
降水量 (mm) 205 150 150 52
请你选择适当的统计图表示这些数据.
统计图的绘制可以不唯一,这个问题,折线统计图和条形统计图都可以,我们应该学会从多个角度来分析数据.
在统计图的选择时,我们应根据三种统计图各自的特点,数据本身的特点,研究问题的需要,来选择适当的统计图.
你能谈谈应该怎样合理选择这三种统计图吗?
议一议
例1 某家电卖场对其销售的空调情况进行了调查,得到了下面的信息:
请你制作适当的统计图,反映下列信息:
例题讲解
解:(1)如图所示.
2012 2013 2014 年份
2 1.5
1.0
0.5
0
销量/万台
2012-2014年,C品牌空调的销售量
(1)2012-2014年,C品牌空调在该卖场销售量的
变化情况;
解:(2)如图所示.
(2)2014年,A,B,C及其他品牌的空调在该卖场的市场
占有率情况.
利用统计图准确表示事物的某个特征
二
甲、乙两种酒近几年的销售量和价格如下:
2002年 2006年 2010年
年度销售量/万瓶 150 180 210
该年度的单价/元 40 50 60
甲品牌酒的产量和价格
2002年 2006年 2010年
年度销售量/万瓶 160 180 200
该年度的单价 40 50 60
乙品牌酒的产量和价格
探究新知
(1)你认为哪一种酒的价格增长较快?为什么?这与上面画出的折线统计图给你的感觉一致吗?为什么图象会给人这样的感觉?
有人根据上面的统计表,制作出甲、乙两种酒的价格变化的折线统计图:
(2)甲种酒的销售人员将甲种酒的销售信息制作成了如下的条形统计图.请你也在右面的图中作出乙种酒的年度销售量的条形统计图:
(3)两幅条形统计图给你的感觉一样吗? 在甲种酒销售人员画的条形统计图中,2010年甲种酒的年度销售量看上去是2002年的多少倍?实际上呢?
(1)为了较直观地比较某两个统计量的变化速度,绘制折线统计图应注意什么?
(2)为了较直观地反映几个统计量之间的比例关系绘制条形统计图时,应注意什么?
在绘制条形统计图时,纵坐标上的起始值应从“0”开始,从而避免造成“误导”、引起“错觉”.
小结
绘制两幅折线统计图,在比较两个统计量的变化趋势时,应注意横(纵)坐标的一致性.
议一议
例2 小明将他的8次数学测验成绩按顺序绘成了如图所示的两幅统计图.
(1)图①和图②给人造成的感觉各是什么?
(2)若小明想向他的父母说明他数学成绩的提高情况,他将向父母展示哪一个统计图?为什么?
例题讲解
解:(1)图①给人的感觉是小明的进步较大,而图②给人的感觉比较平稳,说明小明的进步不是很大.
(2)若小明想向他的父母说明他的数学成绩的提高情况,他将向父母展示图①,因为图①反映小明数学成绩的提高比较明显.
两个统计图中的数学成绩是一样的!
小明绘制了我国2014年和2015年大、中、小学学生人数的扇形统计图,如图(1)(2).根据这个图你能断定我国2015年的大学生人数比2014年多吗?
解:由于不知道这两年的总人数,故不能断定.
[解析] 扇形统计图只能显示各部分在总体中所占的百分比,不同图中的相同对象无法直接比较大小.
做一做
1.七年级七个班开展“学雷锋做好人好事”活动,为了清楚表明三月份各班做好人好事的件数是多少,最好选用( )
A.折线统计图 B.条形统计图
C.扇形统计图 D.都不对
2.某地要反映出2009-2014年降水量的变化情况,应绘制( )
A.条形统计图 B.折线统计图
C.扇形统计图 D.以上都对
B
B
随堂练习
3.如图所示是2010年-2014年期间甲、乙两个公司产品销售情况统计图.由统计图可知,销量增速较快的公司是( )
A.甲公司 B.乙公司
C.一样快 D.无法确定
C
4.某中学七年级(1)班共有学生40人,该班开设了排球、篮球和足球三项体育兴趣课,要求每个学生必须参加,且只能参加其中一项球类运动,图①是该班学生报名后,小明同学经统计而绘制成的条形统计图的一部分.
(1)请你帮小明同学把条形统计图补充完整;
(2)请你根据条形统计图中的数据,改用扇形统计图表示出来(如图②);
解:(1)参加排球兴趣课的有:40-20-12=8(人),如图所示.
(2)从条形统计图可知,参加足球兴趣课的有20人,占总人数的百分比为20÷40×100%=50%,所在扇形圆心角的度数为360°×50%=180°;参加排球兴趣课的有8人,占总人数的百分比为8÷40×100%=20%,所在扇形圆心角的度数为360°×20%=72°;参加篮球兴趣课的有12人,占总人数的百分比为12÷40×100%=30%,所在扇形圆心角的度数为360°×30%=108°,扇形统计图如图②.
足球50%
排球50%
篮球30%
统计图的选择
统计图的选择
统计图引起的错觉
条形统计图注意事项
扇形统计图引起的错觉
折线统计图注意事项
三种统计图的特点
合理选择统计图表示数据
课堂小结
中考链接
1. (2022·广西)空气由多种气体混合而成,为了直观介绍空气中各成分的百分比,最适合使用的统计图是( )
A.条形图 B.折线图 C. 扇形图 D.直方图
2. (2020·牡丹江)在反映某种股票的涨跌情况时,选择( )
A.条形统计图 B. 折线统计图 C.扇形统计图 D.直方图
C
B
当堂测试
1.为研究某种饮料中各成分的百分比,最适合选用的统计图是( )
A.条形统计图 B.图折线统计图
C.扇形统计 D.频数分布直方图
2.要反应一周气温的变化情况,宜采用( )
A.统计表 B. 条形统计图 C. 扇形统计图 D.折线统计图
C
D
当堂测试
4. 在空气的成分中,氮气约占78%,氧气约占21%,其他微量气体约占1%,若要表示以上信息,最合适的统计图是 .
3.要反映我市上周每天的最高气温的变化趋势,最适合采用下列哪种统计图来进行描述( )
A. 条形统计图 B.扇形统计图 C.折线统计图 D.直方图
C
扇形统计图
当堂测试
5.某医院病房护士对一位病人每小时测一次体温,要把这位病人一昼夜体温变化情况用统计图表示出来选用 统计图比较合适(填“条形”、“扇形”、“折线”)
折线
6. 某初中2013年至2022年这十年间入学人数如下表:
当堂测试
根据表格内容,解决下列问题:
(1)若要反映该初中这十年入学人数的变化趋势,最适合的统计图是 .
A.条形统计图
B.扇形统计图
C.折线统计图
(2)与上年相比,该初中入学人数增加最多的年份是 年;
(3)假定每年学生入学后没有转入转出的情况,到2021年底,该初中在校教师总数与在校的三个年级学生总数的比是1:13.如果到2022年底该比值仍不低于1:13,那么2022年该初中在校教师人数至少增加多少?
2022
C
当堂测试
(3)496+517+521=1534(人)1534÷13=118(人)设教师人数增加了x人
解得
答:教师人数至少增加4人.
分层作业
1. 需要清楚地表示每个项目的具体数目应选择( )
A. 折线统计图 B. 扇形统计图
C. 条形统计图 D.以上三者均可
,
【基础达标作业】
2. 下列统计图能够显示数据变化趋势的是( )
A.条形统计图 B. 折线统计图
C.扇形统计图 D.上述统计图都可以
B
C
分层作业
3.下表是我市5月1日-7日最高气温的记录表:
如果要更直观反映我市一周每天的最高气温的变化趋势,你认为应该采用( )
A. 折线统计图 B. 条形统计图
C.频数分布直方图 D.扇形统计图
A
分层作业
【能力提升作业】
4.常见的统计图有条形图、折线图、扇形图、直方图,其中能够显示数据的变化趋势的统计图是 .
5.要表示一个家庭一年用于“教育、服装、食品、其他”这四项的支出各占家庭本年总支出的百分比,最适合采用 统计图.(填“扇形”、“折线”或“条形”)
扇形
折线图
分层作业
【拓展延伸作业】
6. 某校抽查了八(1)班20名学生,测量了他们在800m赛跑后1min的脉搏次数,结果如下(单位:次):144,150,156,165,171,149,162,160,135,159,150,164,168,153,158,139,161,157,154,147.
(1)填写表格
(2)每分钟脉搏次数在150 ≤ x<160这一组的频率是 .(3)若要知道抽测中以上每种范围的人数占总人数的百分比,应选择哪一种统计图?画出你所选择的统计图,并在图中标明相应数据.
解:(1)根据题意,填写表格如下:
(2)每分钟脉搏次数在150 ≤ x<160这一组的频率是 =0.4;
故答案为:0.4
(3)若要知道抽测中以上每种范围的人数占总人数的百分比,应选择扇形统计图,每分钟脉搏次数在130 ≤ x<140这一组的百分比为 ×100%=10%;
每分钟脉博次数在140 ≤ x<150这一组的百分比为 ×100%=15%;
每分钟脉搏次数在150 ≤ x<160这一组的百分比为 ×100%=40%;
每分钟脉搏次数在160 ≤ x<170这一组的百分比为 ×100%=30%;
每分钟脉搏次数在x>170这一组的百分比为 ×100%=5%;
画出扇形统计图,如下:
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
