数学人教A版(2019)选择性必修第二册4.1数列的概念 课件(共31张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.1数列的概念 课件(共31张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 17:07:42 | ||
图片预览








文档简介
(共31张PPT)
4.1 数列的概念
(第一课时)
新知探究:数列的概念
(1):王芳从 1 岁到 17 岁每年的身高依次排成一列数:
75,87,96,103,110, 116,120,128,138,
145,153,158,160,162,163,165,168.
记王芳第岁时的身高为
问: (1) , ,… ,
(2) 之间的顺序能否交换?
是具有确定顺序的一列数
新知探究:数列的概念
(2):在两河流域发掘的一块泥版上,有一列依次表示一个月中从第1天到第15天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,144,
160,176,192,208,224,240.
的次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数:
是具有确定顺序的一列数
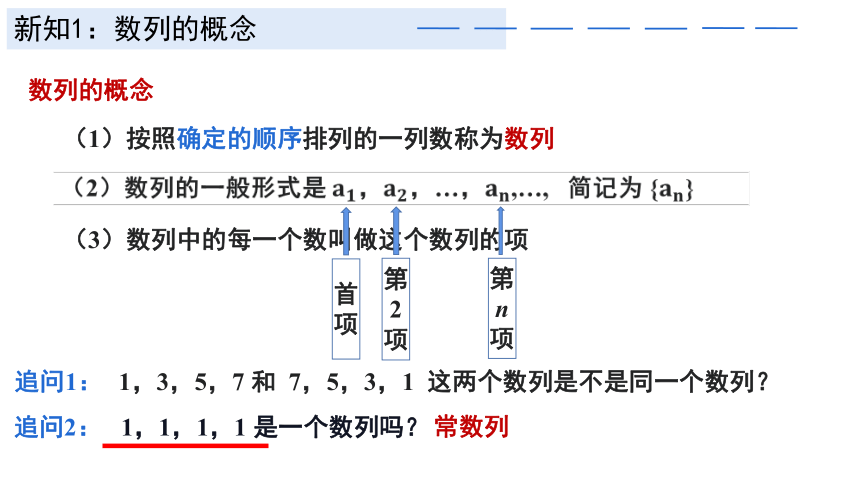
新知1:数列的概念
数列的概念
(1)按照确定的顺序排列的一列数称为数列
(2)数列的一般形式是 ,,…,,…, 简记为 {}
(3)数列中的每一个数叫做这个数列的项
首项
第2项
第n项
追问1: 1,3,5,7 和 7,5,3,1 这两个数列是不是同一个数列?
追问2: 1,1,1,1 是一个数列吗?
常数列
新知1:数列的概念
①王芳的身高:75,87,96,103,110, 116,120,128,138
②
有穷数列
无穷数列
思考1:符号与所表示的意义是否相同?
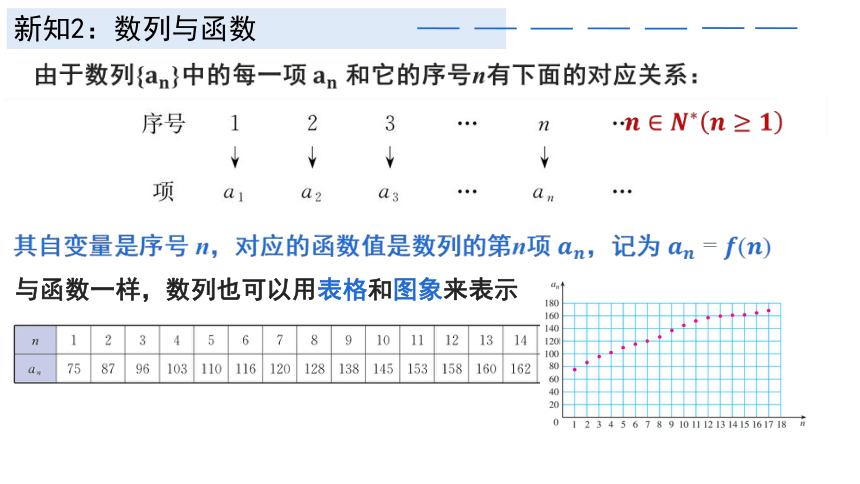
新知2:数列与函数
由于数列{}中的每一项 和它的序号n有下面的对应关系:
其自变量是序号 n,对应的函数值是数列的第n项 ,记为
与函数一样,数列也可以用表格和图象来表示
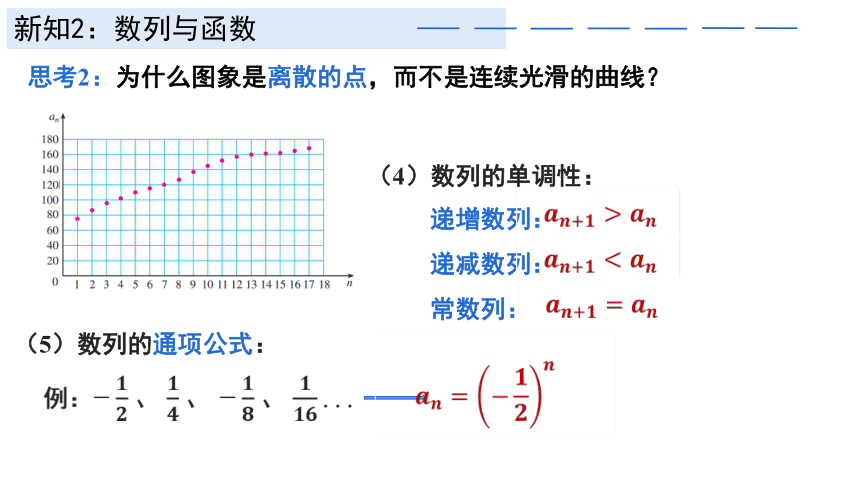
新知2:数列与函数
思考2:为什么图象是离散的点,而不是连续光滑的曲线?
(4)数列的单调性:
递增数列:
递减数列:
常数列:
(5)数列的通项公式:
例:
例题精讲
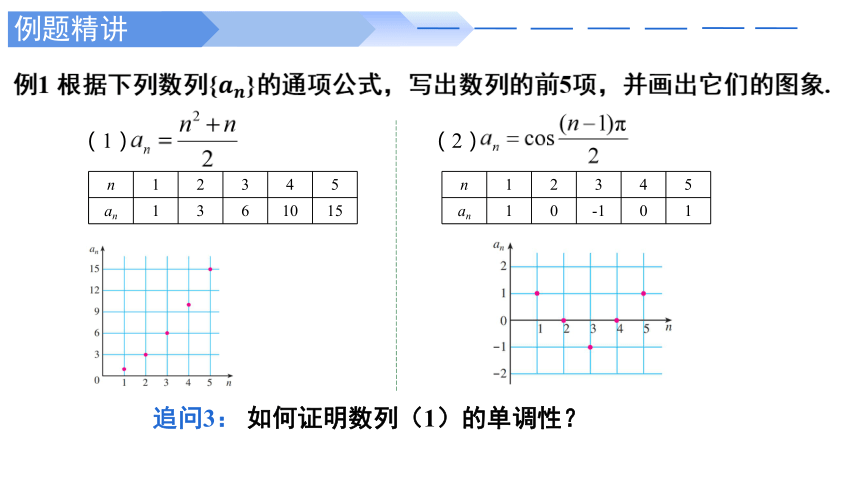
例1 根据下列数列{}的通项公式,写出数列的前5项,并画出它们的图象.
n 1 2 3 4 5
an
(1)
(2)
n 1 2 3 4 5
an 1 0 -1 0 1
1 3 6 10 15
追问3: 如何证明数列(1)的单调性?
例题精讲
例2 根据下列数列的前项,写出数列的一个通项公式:
摆动数列:
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
典例分析
课本P9题7
课堂小结
我们学习了哪些新知识、新的数学思想、方法?
1)数列的概念
2)数列的符号表示
3)数列的分类
(数列是特殊的函数)
4)数列的表示方法
5)数列的通项公式
特殊到一般的思想,类比的方法
课堂作业
4.1 数列的概念
(第二课时)
复习回顾:
数列的概念
(1)按照确定的顺序排列的一列数称为数列
(2)数列的一般形式是 ,,…,,…, 简记为 {}
(3)数列中的每一个数叫做这个数列的项
(4)数列的单调性:
(5)数列的通项公式:
教学内容:
一、教学目标
1.理解数列递推公式的含义,会用递推公式解决有关问题。
2.了解通项公式和递推公式是给出数列的两种方式,并明确它们的异同。
3.会利用数列的前n项和与通项的关系求通项公式。
二、教学重难点
1、教学重点
理解递推公式的含义.
2、教学难点
会用递推公式解决有关问题,用数列的前n项和与通项的关系求通项公式
典例分析
例3 如果数列{}的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
追问4:已知通项公式,我们能解决什么问题呢?
1.知道数列中某一项的值;
2.判断一个数是否是该数列的项.
探究:除了通项公式、列表法以及图象法外,数列还有其它的表示方法吗?
典例分析
例4 下列图中的4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的一个通项公式.
1
3
9
27
数列的通项公式:
追问5:项与项之间有什么关系?
×3
×3
×3
从第二项起,后一项是前一项的三倍
新知3:数列的递推公式
递推公式
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
例5 已知数列的第项是,以后的各项由公式 给出,写出这个数列的前项.
注:的下标要
追问6:递推公式有什么作用呢?
1.知道首项和递推公式的条件下,可以求出数列的每一项;
2.知道项与项之间的关系.
典例分析
课本P9题4
新知3:数列的递推公式
追问7:递推公式和通项公式有什么联系和区别?
相同点 不同点
通项公式 均可确定一个 数列,求出数列中的任意一项. 给出的值,可求出数列中的第项.
递推公式 由前一项(或前几项),通过一次(或多次)运算,可求出第项.
新知4:数列的前项和
在对数列的研究中,求数列某些项的和是主要问题之一.
我们把数列{}从第1项起到第n项止的各项之和,称为数列{}的前n项和,记作,即
如果数列的前项和与它的序号之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前项和公式.
显然,而,于是我们有
与的关系式
典例分析
例6 已知数列的前项和公式为,你能求出的通项公式吗?
由 求需要检验
典例分析
练1. 已知数列{an}的前n项和为 ,求这个数列的通项公式.
练2.已知数列的前项和公式为 ,求通项公式 .
小结
由数列的前项和求通项公式的三个步骤
1)求
2)当
3)最后验证,当课堂练习
课堂练习
能力提升
1.已知数列{an}满足 a1 = 1,an = an-1+1 (n ≥ 2), 写出这个数列的通项公式.
解:由递推式可得,
a2-a1 = 1,
a3-a2 = 1,
…
an-an-1 = 1
把以上 n-1 个式子相加,得 an -a1 = n -1
∴数列的通项为 an = n.
总结:一般递推关系为an+1= f (n)+an,即an+1 - an = f (n)时,可用累加法求通项公式.
又 a1 = 1
能力提升
2.已知数列{an}满足 写出这个数列的通项公式.
解:由递推式可得
∴数列的通项为 .
把以上n-1个式子相乘得
又 a1 = 1
总结:一般递推关系为an+1= f (n)·an, 即 时,可用累乘法求通项公式.
能力提升
3. 已知数列 {an} 的前 n 项和公式 Sn ,求数列{an}的通项公式.
(1)Sn = 2n2-n+1, (2)Sn = log2 (n+1)
解:(1)当 n ≥ 2 时,
故数列{an}的通项公式为
当n = 1时, 不符合上式
能力提升
解: (2)当 n ≥ 2 时,
当n = 1时, ,符合上式
故数列{an}的通项公式为
总结:已知Sn求出an依据的是Sn的定义:Sn=a1+a2+…+an,分段求解,然后检验结果能否统一形式,能就写成一个,否则只能写成分段函数的形式.
课堂小结
4.1 数列的概念
(第一课时)
新知探究:数列的概念
(1):王芳从 1 岁到 17 岁每年的身高依次排成一列数:
75,87,96,103,110, 116,120,128,138,
145,153,158,160,162,163,165,168.
记王芳第岁时的身高为
问: (1) , ,… ,
(2) 之间的顺序能否交换?
是具有确定顺序的一列数
新知探究:数列的概念
(2):在两河流域发掘的一块泥版上,有一列依次表示一个月中从第1天到第15天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,144,
160,176,192,208,224,240.
的次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数:
是具有确定顺序的一列数
新知1:数列的概念
数列的概念
(1)按照确定的顺序排列的一列数称为数列
(2)数列的一般形式是 ,,…,,…, 简记为 {}
(3)数列中的每一个数叫做这个数列的项
首项
第2项
第n项
追问1: 1,3,5,7 和 7,5,3,1 这两个数列是不是同一个数列?
追问2: 1,1,1,1 是一个数列吗?
常数列
新知1:数列的概念
①王芳的身高:75,87,96,103,110, 116,120,128,138
②
有穷数列
无穷数列
思考1:符号与所表示的意义是否相同?
新知2:数列与函数
由于数列{}中的每一项 和它的序号n有下面的对应关系:
其自变量是序号 n,对应的函数值是数列的第n项 ,记为
与函数一样,数列也可以用表格和图象来表示
新知2:数列与函数
思考2:为什么图象是离散的点,而不是连续光滑的曲线?
(4)数列的单调性:
递增数列:
递减数列:
常数列:
(5)数列的通项公式:
例:
例题精讲
例1 根据下列数列{}的通项公式,写出数列的前5项,并画出它们的图象.
n 1 2 3 4 5
an
(1)
(2)
n 1 2 3 4 5
an 1 0 -1 0 1
1 3 6 10 15
追问3: 如何证明数列(1)的单调性?
例题精讲
例2 根据下列数列的前项,写出数列的一个通项公式:
摆动数列:
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列.
典例分析
课本P9题7
课堂小结
我们学习了哪些新知识、新的数学思想、方法?
1)数列的概念
2)数列的符号表示
3)数列的分类
(数列是特殊的函数)
4)数列的表示方法
5)数列的通项公式
特殊到一般的思想,类比的方法
课堂作业
4.1 数列的概念
(第二课时)
复习回顾:
数列的概念
(1)按照确定的顺序排列的一列数称为数列
(2)数列的一般形式是 ,,…,,…, 简记为 {}
(3)数列中的每一个数叫做这个数列的项
(4)数列的单调性:
(5)数列的通项公式:
教学内容:
一、教学目标
1.理解数列递推公式的含义,会用递推公式解决有关问题。
2.了解通项公式和递推公式是给出数列的两种方式,并明确它们的异同。
3.会利用数列的前n项和与通项的关系求通项公式。
二、教学重难点
1、教学重点
理解递推公式的含义.
2、教学难点
会用递推公式解决有关问题,用数列的前n项和与通项的关系求通项公式
典例分析
例3 如果数列{}的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
追问4:已知通项公式,我们能解决什么问题呢?
1.知道数列中某一项的值;
2.判断一个数是否是该数列的项.
探究:除了通项公式、列表法以及图象法外,数列还有其它的表示方法吗?
典例分析
例4 下列图中的4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的一个通项公式.
1
3
9
27
数列的通项公式:
追问5:项与项之间有什么关系?
×3
×3
×3
从第二项起,后一项是前一项的三倍
新知3:数列的递推公式
递推公式
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
例5 已知数列的第项是,以后的各项由公式 给出,写出这个数列的前项.
注:的下标要
追问6:递推公式有什么作用呢?
1.知道首项和递推公式的条件下,可以求出数列的每一项;
2.知道项与项之间的关系.
典例分析
课本P9题4
新知3:数列的递推公式
追问7:递推公式和通项公式有什么联系和区别?
相同点 不同点
通项公式 均可确定一个 数列,求出数列中的任意一项. 给出的值,可求出数列中的第项.
递推公式 由前一项(或前几项),通过一次(或多次)运算,可求出第项.
新知4:数列的前项和
在对数列的研究中,求数列某些项的和是主要问题之一.
我们把数列{}从第1项起到第n项止的各项之和,称为数列{}的前n项和,记作,即
如果数列的前项和与它的序号之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前项和公式.
显然,而,于是我们有
与的关系式
典例分析
例6 已知数列的前项和公式为,你能求出的通项公式吗?
由 求需要检验
典例分析
练1. 已知数列{an}的前n项和为 ,求这个数列的通项公式.
练2.已知数列的前项和公式为 ,求通项公式 .
小结
由数列的前项和求通项公式的三个步骤
1)求
2)当
3)最后验证,当
课堂练习
能力提升
1.已知数列{an}满足 a1 = 1,an = an-1+1 (n ≥ 2), 写出这个数列的通项公式.
解:由递推式可得,
a2-a1 = 1,
a3-a2 = 1,
…
an-an-1 = 1
把以上 n-1 个式子相加,得 an -a1 = n -1
∴数列的通项为 an = n.
总结:一般递推关系为an+1= f (n)+an,即an+1 - an = f (n)时,可用累加法求通项公式.
又 a1 = 1
能力提升
2.已知数列{an}满足 写出这个数列的通项公式.
解:由递推式可得
∴数列的通项为 .
把以上n-1个式子相乘得
又 a1 = 1
总结:一般递推关系为an+1= f (n)·an, 即 时,可用累乘法求通项公式.
能力提升
3. 已知数列 {an} 的前 n 项和公式 Sn ,求数列{an}的通项公式.
(1)Sn = 2n2-n+1, (2)Sn = log2 (n+1)
解:(1)当 n ≥ 2 时,
故数列{an}的通项公式为
当n = 1时, 不符合上式
能力提升
解: (2)当 n ≥ 2 时,
当n = 1时, ,符合上式
故数列{an}的通项公式为
总结:已知Sn求出an依据的是Sn的定义:Sn=a1+a2+…+an,分段求解,然后检验结果能否统一形式,能就写成一个,否则只能写成分段函数的形式.
课堂小结
