八年级上册第一学期期中水平测试题(D)
图片预览

文档简介
八年级上册第一学期期中水平测试题(D)
一、认认真真选,沉着应战!
1.若,那么不等式的值一定是( )
A.负数 B.正数 C.非负数 D.正、负数不能唯一确定
2. 若分式不论取何实数时总有意义,则的取值范围是( )
A、 B、 C、 D、
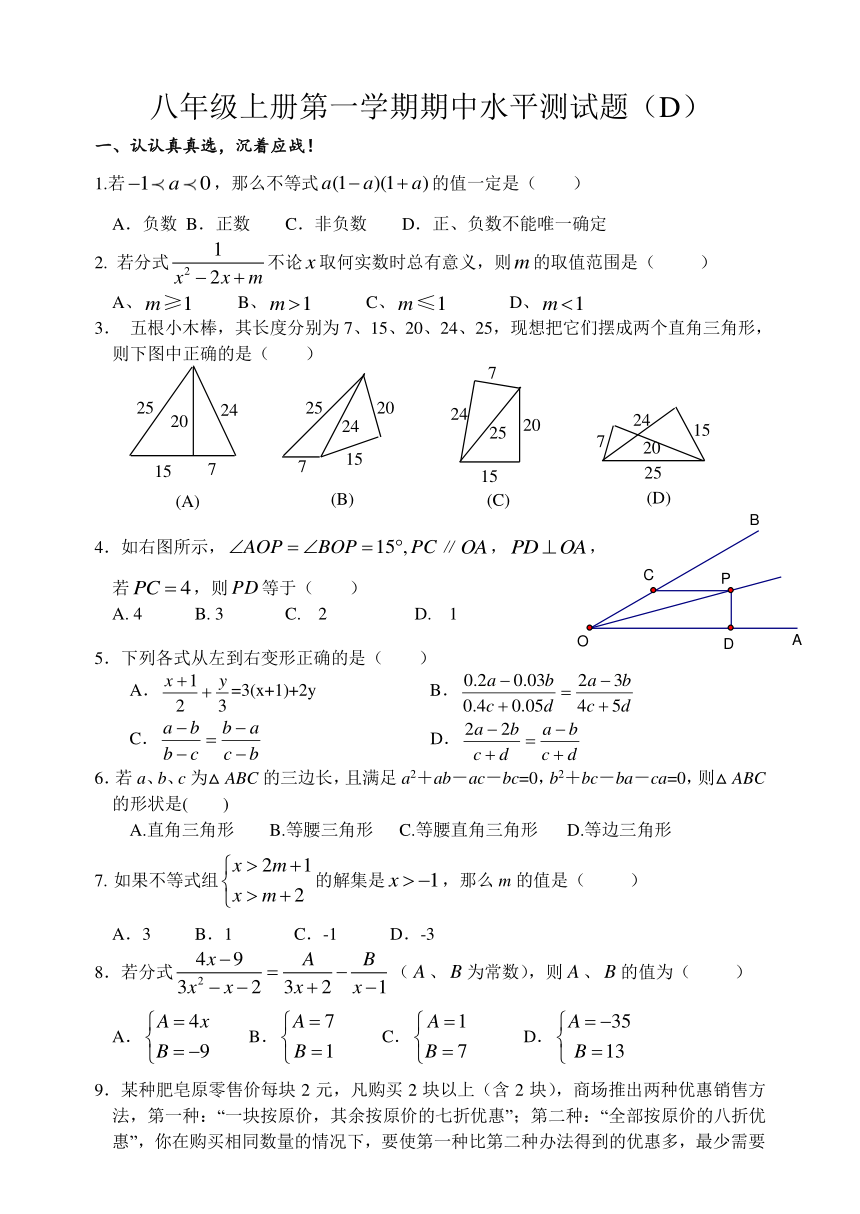
3. 五根小木棒,其长度分别为7、15、20、24、25,现想把它们摆成两个直角三角形,则下图中正确的是( )
4.如右图所示,∥,,
若,则等于( )
A. 4 B. 3 C. 2 D. 1
5.下列各式从左到右变形正确的是( )
A.=3(x+1)+2y B.
C. D.
6.若a、b、c为△ABC的三边长,且满足a2+ab-ac-bc=0,b2+bc-ba-ca=0,则△ABC的形状是( )
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
7. 如果不等式组的解集是,那么m的值是( )
A.3 B.1 C.-1 D.-3
8.若分式(、为常数),则、的值为( )
A. B. C. D.
9.某种肥皂原零售价每块2元,凡购买2块以上(含2块),商场推出两种优惠销售方法,第一种:“一块按原价,其余按原价的七折优惠”;第二种:“全部按原价的八折优惠”,你在购买相同数量的情况下,要使第一种比第二种办法得到的优惠多,最少需要购买肥皂( )
A.5块 B.4块 C.3块 D.2块
10. 一平面镜以于水平面成交固定在水平桌面上,如右图所示,
一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平
面镜里所成的像( )
A.以1米/秒的速度,做竖直向上运动 B.以1米/秒的速度,做竖直向下运动
C.以2米/秒的速度,做竖直向上运动 D.以2米/秒的速度,做竖直向下运动
二、仔仔细细填,记录自信!
11.写出一个含有字母的分式(要求:不论取任何实数,该分式都有意义,且分式的值为负)__________________.
12.小明把一根70cm长的木棒放到一个长、宽、高分别为50cm、40cm、30cm的木箱中,他能放进去吗?答:_______________(填“能”、或“不能”)
13. 若关于的不等式的解集为,则关于的不等式的解集为_________.
14.对于整数,符号表示运算,已知,则的值是________.
15. 在中,的对边分别是,若,又,则最大边上的高为________.
16. 若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为________.
17.观察下列有规律的数:,,,,,,…,根据其规律可知第个数为_____________(为正整数).
18. 如图所示,是一个钢架,且,为了使钢架更加牢固,需在内部添加一些钢管…,添加的钢管长度都与相等,则最多能添加这样的钢管_______根.
19. 一艘船由至顺水航行每小时走千米,由至逆水航行每小时走千米,则此船在、间往返一次平均每小时走__________千米.
20.某种出租车的收费标准是:起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米以后,每增加1千米,加收2.4元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,那么x的最大值是________.
三、平心静气做,展示智慧!
21.若关于,的二元一次方程组的解,都是正数,试求的取值范围.
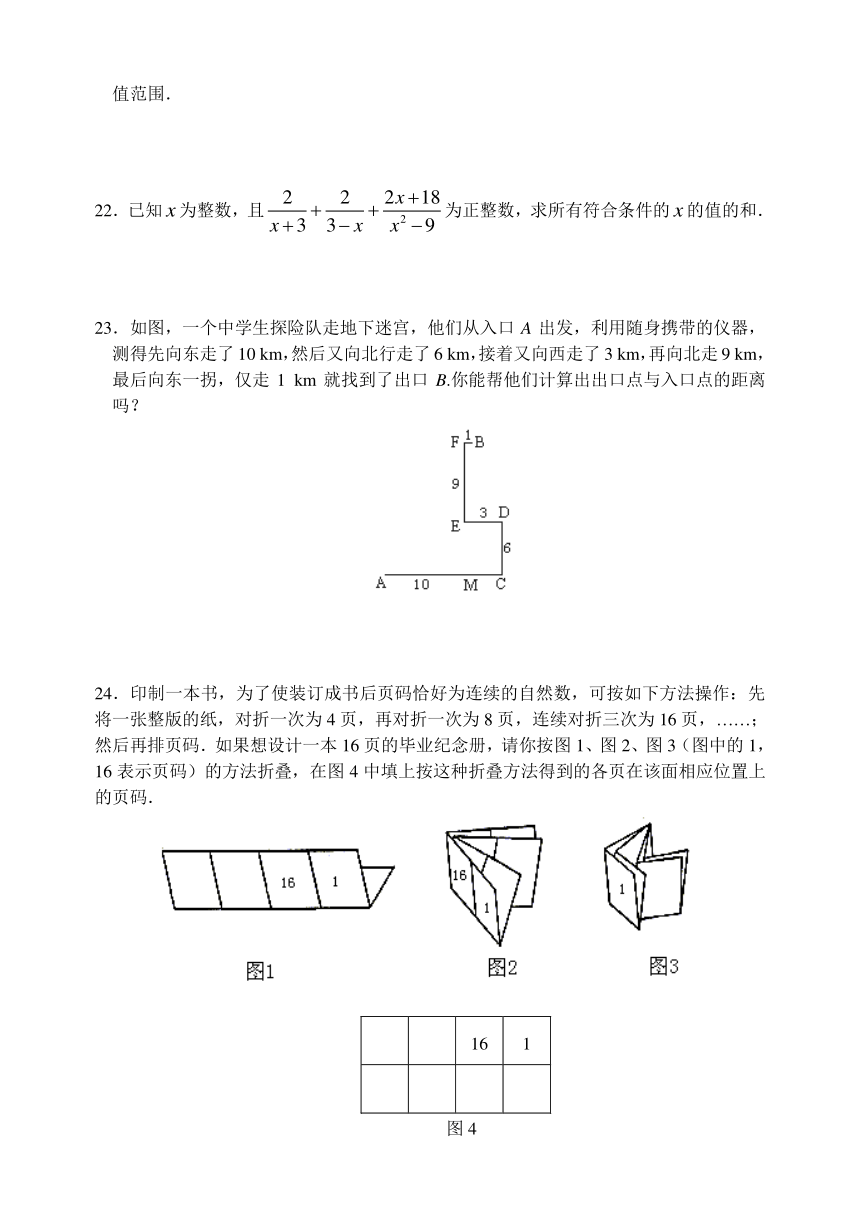
22.已知为整数,且为正整数,求所有符合条件的的值的和.
23.如图,一个中学生探险队走地下迷宫,他们从入口A出发,利用随身携带的仪器,测得先向东走了10 km,然后又向北行走了6 km,接着又向西走了3 km,再向北走9 km,最后向东一拐,仅走1 km就找到了出口B.你能帮他们计算出出口点与入口点的距离吗?
24.印制一本书,为了使装订成书后页码恰好为连续的自然数,可按如下方法操作:先将一张整版的纸,对折一次为4页,再对折一次为8页,连续对折三次为16页,……;然后再排页码.如果想设计一本16页的毕业纪念册,请你按图1、图2、图3(图中的1,16表示页码)的方法折叠,在图4中填上按这种折叠方法得到的各页在该面相应位置上的页码.
25.某公司计划一年度生产一种新型计算机,下面是各部门提供的数值信息:
人事部:明年生产工人不多于80人,每人每年按2400工时计算;
市场部:预测明年销售量至少为10000台;技术部:生产一台计算机,平均要用12个工时,每台机器需要安装5个主要部件;
供应部:今年年终将库存主要部件2000件,明年还能采购到此种部件80000件.
根据上述信息,试判断明年该公司的生产量可能是多少
26.公园里两条小河在处汇合,两河形成的小岛
上有一处古迹,如图7,现计划在两条小河上各建一座小
桥与,并在岛上修三段小路,连通两座小桥与古迹,
这两座小桥应建在何处,才能使修路费用最少
27.印度数学家什迦逻(1141年-1225年)在其著作中曾提出过有趣的“荷花问题”,这个问题是以诗歌的形式出现的:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
请用学过的数学知识回答这个问题.
四、发散思维,游刃有余!
28.探索问题:
(1)请你任意写出5个正的真分数:____、_____、_____、_____、_____,给每个分数的分子和分母同加一个正数得到五个新分数:____、_____、_____、_____、_____.
(2)比较原来的每个分数与对应新分数的大小,可以得出下面的结论:
一个真分数是(、均为正数),给其分子、分母同加一个正数,得,则两个分数的大小关系是:______.
(3)请你用文字叙述(2)中结论的含义:_________________________.
(4)你能用图形的面积说明这个结论吗?
(5)这个结论可以解释生活中的许多现象,解决许多生活与数学中的问题.请你举出一个生活中与此结论相关的例子.
参考答案
一、1—5:BBCCC 6—10:DDBBB
二、 11.略
12.能
13.
14. 3或-3
15. 2.4
16. 或
17.
18.8
19.
20.8
三、 21.
22.,由已知得为正整数,所以可取4、5.
所以
23.过点B作BM⊥AC于点M,连结AB.
在Rt△ABM中,AM=10-3+1=8,BM=6+9=15,
所以AB2=AM2+BM2=82+152=289.故AB=17(km),
即出口点与入口点的距离是17 km.
24.
25.设明年生产x台计算机,于是有,解得,所以,而明年的销售量至少是10000台,所以这个公司的生产量应安排在10000台至16000台之间.
26.作点关于的对称点,关于的对称点,连结,分别交,于、.
27. 设水深为x尺,则荷花原高为(x+0.5)尺,据题意得,
解得
四、
28. (1)略;
(2)>;
(3)把一个正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数.
(4)如右图所示,由可得
,则,即,
,不等式两边都除以即可得
到.
(5)比如:
①一杯克糖水,内含克糖,糖水浓度,若再往杯中加克糖,现在糖水的浓度是,比加糖前的浓度增大了,所以糖水变甜了;②建筑学规定:民用住宅的窗户面积必须小于地板面积,但按采光标准,窗户面积和地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,若同时增加相等的窗户面积和地板面积,根据结论住宅的采光条件将会变得更好.
N
M
P
O
20
7
15
25
24
24
15
20
7
25
20
24
15
7
25
7
15
20
24
25
(A)
(B)
(C)
(D)
一、认认真真选,沉着应战!
1.若,那么不等式的值一定是( )
A.负数 B.正数 C.非负数 D.正、负数不能唯一确定
2. 若分式不论取何实数时总有意义,则的取值范围是( )
A、 B、 C、 D、
3. 五根小木棒,其长度分别为7、15、20、24、25,现想把它们摆成两个直角三角形,则下图中正确的是( )
4.如右图所示,∥,,
若,则等于( )
A. 4 B. 3 C. 2 D. 1
5.下列各式从左到右变形正确的是( )
A.=3(x+1)+2y B.
C. D.
6.若a、b、c为△ABC的三边长,且满足a2+ab-ac-bc=0,b2+bc-ba-ca=0,则△ABC的形状是( )
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
7. 如果不等式组的解集是,那么m的值是( )
A.3 B.1 C.-1 D.-3
8.若分式(、为常数),则、的值为( )
A. B. C. D.
9.某种肥皂原零售价每块2元,凡购买2块以上(含2块),商场推出两种优惠销售方法,第一种:“一块按原价,其余按原价的七折优惠”;第二种:“全部按原价的八折优惠”,你在购买相同数量的情况下,要使第一种比第二种办法得到的优惠多,最少需要购买肥皂( )
A.5块 B.4块 C.3块 D.2块
10. 一平面镜以于水平面成交固定在水平桌面上,如右图所示,
一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平
面镜里所成的像( )
A.以1米/秒的速度,做竖直向上运动 B.以1米/秒的速度,做竖直向下运动
C.以2米/秒的速度,做竖直向上运动 D.以2米/秒的速度,做竖直向下运动
二、仔仔细细填,记录自信!
11.写出一个含有字母的分式(要求:不论取任何实数,该分式都有意义,且分式的值为负)__________________.
12.小明把一根70cm长的木棒放到一个长、宽、高分别为50cm、40cm、30cm的木箱中,他能放进去吗?答:_______________(填“能”、或“不能”)
13. 若关于的不等式的解集为,则关于的不等式的解集为_________.
14.对于整数,符号表示运算,已知,则的值是________.
15. 在中,的对边分别是,若,又,则最大边上的高为________.
16. 若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为________.
17.观察下列有规律的数:,,,,,,…,根据其规律可知第个数为_____________(为正整数).
18. 如图所示,是一个钢架,且,为了使钢架更加牢固,需在内部添加一些钢管…,添加的钢管长度都与相等,则最多能添加这样的钢管_______根.
19. 一艘船由至顺水航行每小时走千米,由至逆水航行每小时走千米,则此船在、间往返一次平均每小时走__________千米.
20.某种出租车的收费标准是:起步价7元(即行驶距离不超过3千米都需付7元车费),超过3千米以后,每增加1千米,加收2.4元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,那么x的最大值是________.
三、平心静气做,展示智慧!
21.若关于,的二元一次方程组的解,都是正数,试求的取值范围.
22.已知为整数,且为正整数,求所有符合条件的的值的和.
23.如图,一个中学生探险队走地下迷宫,他们从入口A出发,利用随身携带的仪器,测得先向东走了10 km,然后又向北行走了6 km,接着又向西走了3 km,再向北走9 km,最后向东一拐,仅走1 km就找到了出口B.你能帮他们计算出出口点与入口点的距离吗?
24.印制一本书,为了使装订成书后页码恰好为连续的自然数,可按如下方法操作:先将一张整版的纸,对折一次为4页,再对折一次为8页,连续对折三次为16页,……;然后再排页码.如果想设计一本16页的毕业纪念册,请你按图1、图2、图3(图中的1,16表示页码)的方法折叠,在图4中填上按这种折叠方法得到的各页在该面相应位置上的页码.
25.某公司计划一年度生产一种新型计算机,下面是各部门提供的数值信息:
人事部:明年生产工人不多于80人,每人每年按2400工时计算;
市场部:预测明年销售量至少为10000台;技术部:生产一台计算机,平均要用12个工时,每台机器需要安装5个主要部件;
供应部:今年年终将库存主要部件2000件,明年还能采购到此种部件80000件.
根据上述信息,试判断明年该公司的生产量可能是多少
26.公园里两条小河在处汇合,两河形成的小岛
上有一处古迹,如图7,现计划在两条小河上各建一座小
桥与,并在岛上修三段小路,连通两座小桥与古迹,
这两座小桥应建在何处,才能使修路费用最少
27.印度数学家什迦逻(1141年-1225年)在其著作中曾提出过有趣的“荷花问题”,这个问题是以诗歌的形式出现的:
“平平湖水清可鉴,面上半尺生红莲;
出泥不染亭亭立,忽被强风吹一边,
渔人观看忙向前,花离原位二尺远;
能算诸君请解题,湖水如何知深浅?”
请用学过的数学知识回答这个问题.
四、发散思维,游刃有余!
28.探索问题:
(1)请你任意写出5个正的真分数:____、_____、_____、_____、_____,给每个分数的分子和分母同加一个正数得到五个新分数:____、_____、_____、_____、_____.
(2)比较原来的每个分数与对应新分数的大小,可以得出下面的结论:
一个真分数是(、均为正数),给其分子、分母同加一个正数,得,则两个分数的大小关系是:______.
(3)请你用文字叙述(2)中结论的含义:_________________________.
(4)你能用图形的面积说明这个结论吗?
(5)这个结论可以解释生活中的许多现象,解决许多生活与数学中的问题.请你举出一个生活中与此结论相关的例子.
参考答案
一、1—5:BBCCC 6—10:DDBBB
二、 11.略
12.能
13.
14. 3或-3
15. 2.4
16. 或
17.
18.8
19.
20.8
三、 21.
22.,由已知得为正整数,所以可取4、5.
所以
23.过点B作BM⊥AC于点M,连结AB.
在Rt△ABM中,AM=10-3+1=8,BM=6+9=15,
所以AB2=AM2+BM2=82+152=289.故AB=17(km),
即出口点与入口点的距离是17 km.
24.
25.设明年生产x台计算机,于是有,解得,所以,而明年的销售量至少是10000台,所以这个公司的生产量应安排在10000台至16000台之间.
26.作点关于的对称点,关于的对称点,连结,分别交,于、.
27. 设水深为x尺,则荷花原高为(x+0.5)尺,据题意得,
解得
四、
28. (1)略;
(2)>;
(3)把一个正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数.
(4)如右图所示,由可得
,则,即,
,不等式两边都除以即可得
到.
(5)比如:
①一杯克糖水,内含克糖,糖水浓度,若再往杯中加克糖,现在糖水的浓度是,比加糖前的浓度增大了,所以糖水变甜了;②建筑学规定:民用住宅的窗户面积必须小于地板面积,但按采光标准,窗户面积和地板面积的比应不小于10%,并且这个比值越大,住宅的采光条件越好,若同时增加相等的窗户面积和地板面积,根据结论住宅的采光条件将会变得更好.
N
M
P
O
20
7
15
25
24
24
15
20
7
25
20
24
15
7
25
7
15
20
24
25
(A)
(B)
(C)
(D)
同课章节目录
