6.多边形的面积——梯形的面积同步练习(含解析)人教版五年级数学上册
文档属性
| 名称 | 6.多边形的面积——梯形的面积同步练习(含解析)人教版五年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 245.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 15:14:01 | ||
图片预览



文档简介
6.多边形的面积——梯形的面积同步练习 (含答案)
人教版 五年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积公式是( )。
2.一个梯形的上底是5dm,下底是上底的1.2倍,高是4dm,这个梯形的面积是( )。
3.两个完全一样的梯形可以拼成一个平行四边形,拼成的平行四边形的底等于梯形的( ),高等于梯形的( )。由平行四边形面积=底×高,可推出梯形面积=( )。
4.我国古代数学家刘徽利用出入相补原理来计算平面图形的面积。把一个梯形沿着两腰中点的连线剪开,旋转后拼成了一个平行四边形(如图)。原图中梯形的面积是( )平方厘米。
5.两个完全一样的梯形拼成一个平行四边形,如果这个平行四边形的面积是80,那么每个梯形的面积是( )。
6.一张梯形纸片的上底是4dm,下底比上底长5dm,高是8dm,面积是( )dm2,如果从中剪去一个最大的三角形,这个三角形的面积是( )dm2。
7.一个梯形的装饰板,上底9分米,下底11分米,高1.2米,两面都要涂油漆,涂油漆的面积是( )平方分米。
二、选择题
8.如图,在平行线之间有三个图形,它们的面积相比较,( )。
A.平行四边形的面积最大 B.三角形面积最大 C.一样大
9.一堆钢管,最下层有8根,最上层有1根,每相邻两层相差1根,这堆钢管共有( )根。
A.72 B.32 C.36
10.将一个平行四边形沿高剪开,不可能得到( )。
A.一个平行四边形和一个梯形 B.两个三角形 C.两个梯形
11.把一个平行四边形任意分割成两个梯形,这两个梯形的( )总是相等的。
A.面积 B.周长 C.高
12.如图所示,把一个长方形分成一个梯形和一个三角形。已知梯形的面积比三角形的面积大30cm2,那么梯形的上底是( )。
A.3cm B.4cm C.5cm
13.用65米的篱笆靠端墙围城一个梯形的养鸡场(如图),这个养鸡场占地面积是( )平方米。
A.1320 B.880 C.450
14.如图:梯形内有①、②两个三角形,则①、②两个三角形的面积关系是( )。
A.S①>S② B.S①<S② C.S①=S②
15.一个梯形的上底增加3厘米后就变成一个边长6厘米的正方形,这个梯形的面积是( )平方厘米。
A.27 B.36 C.48
16.一堆大小相同的圆木,堆成梯形形状,最下层有12根,最上层有6根,共堆了5层,这堆圆木共有( )。
A.51根 B.45根 C.66根
三、判断题
17.一个梯形的上底、下底和高都乘2,面积就扩大到原来的2倍。( )
18.连接梯形上底和下底的中点,把它分成2个小梯形,它们的周长相等。( )
19.两个等底等高的平行四边形一定可以拼成一个梯形。( )
20.梯形的上底减少2cm,高增加2cm,它的面积不变。( )
21.两个一样的直角梯形,可以拼成一个平行四边形。( )
四、计算下面每个梯形的面积
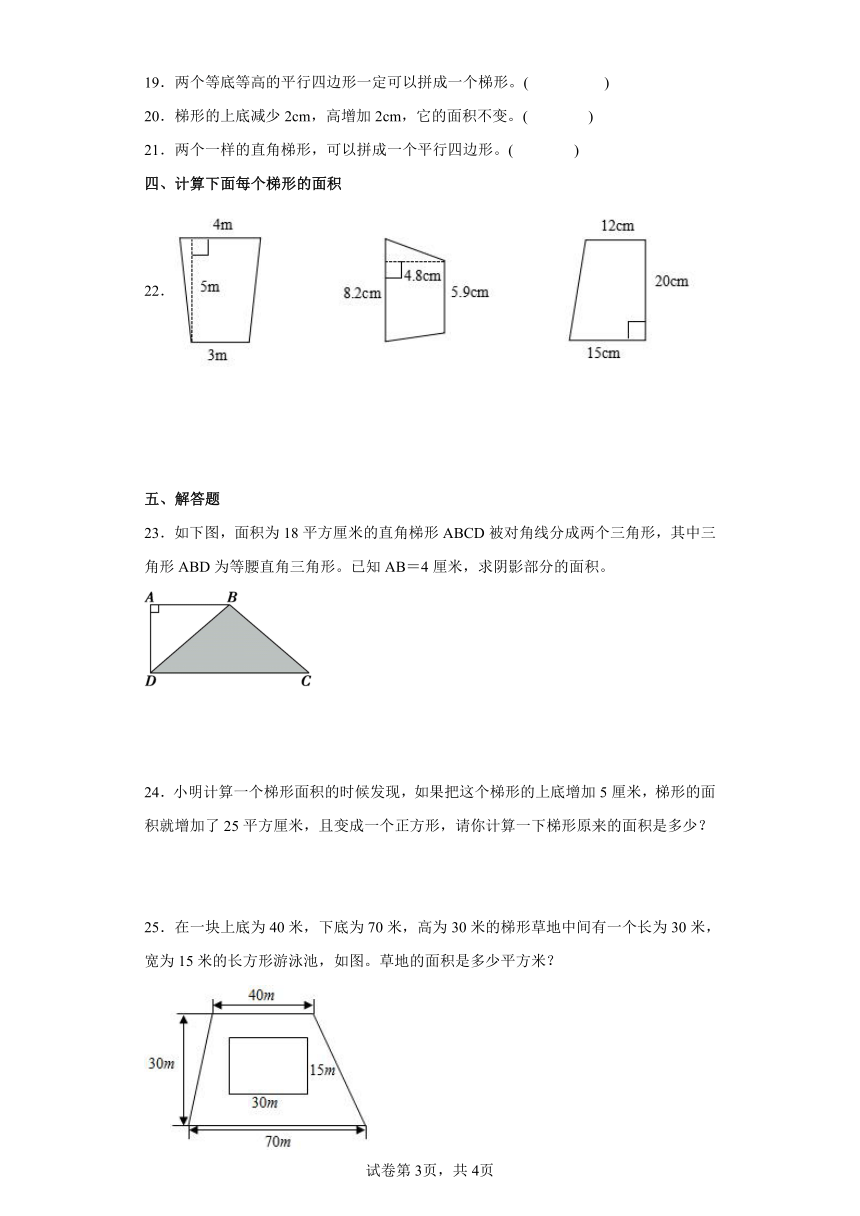
22.
五、解答题
23.如下图,面积为18平方厘米的直角梯形ABCD被对角线分成两个三角形,其中三角形ABD为等腰直角三角形。已知AB=4厘米,求阴影部分的面积。
24.小明计算一个梯形面积的时候发现,如果把这个梯形的上底增加5厘米,梯形的面积就增加了25平方厘米,且变成一个正方形,请你计算一下梯形原来的面积是多少?
25.在一块上底为40米,下底为70米,高为30米的梯形草地中间有一个长为30米,宽为15米的长方形游泳池,如图。草地的面积是多少平方米?
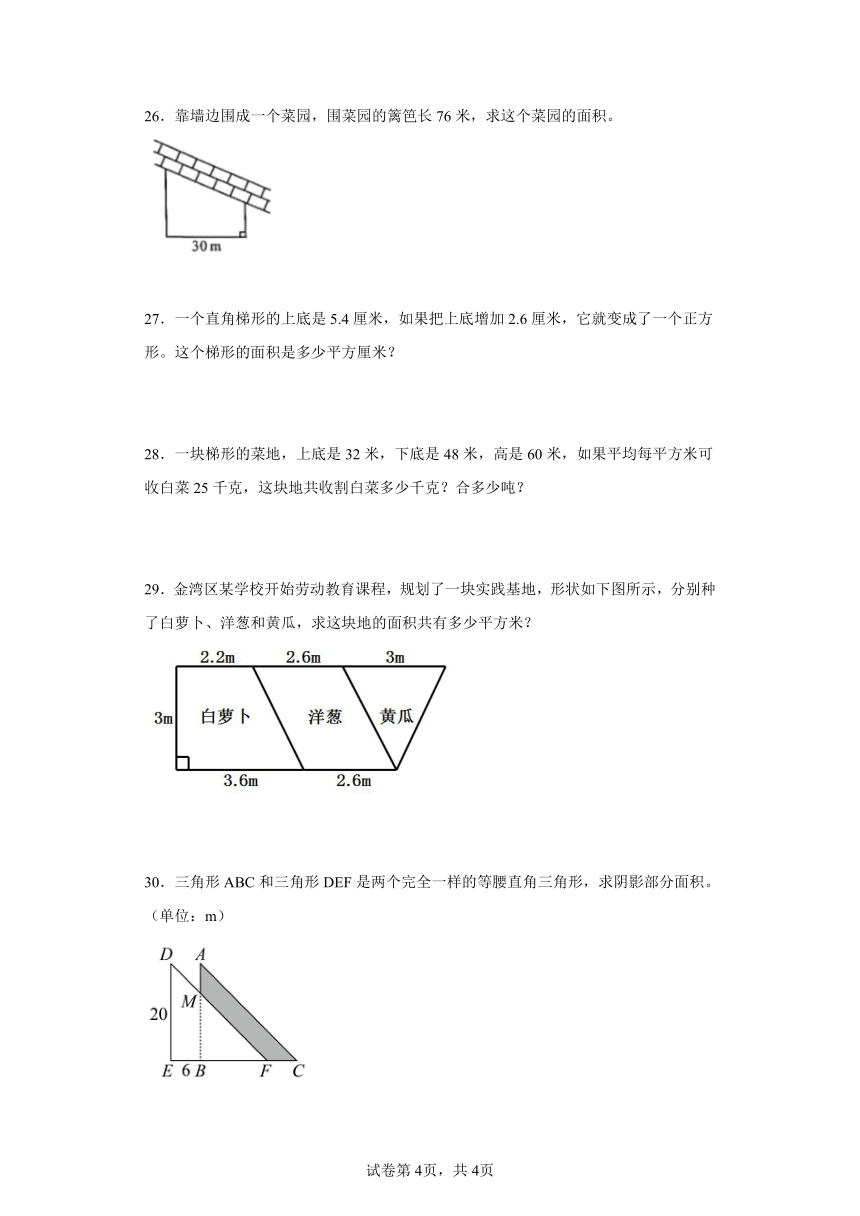
26.靠墙边围成一个菜园,围菜园的篱笆长76米,求这个菜园的面积。
27.一个直角梯形的上底是5.4厘米,如果把上底增加2.6厘米,它就变成了一个正方形。这个梯形的面积是多少平方厘米?
28.一块梯形的菜地,上底是32米,下底是48米,高是60米,如果平均每平方米可收白菜25千克,这块地共收割白菜多少千克?合多少吨?
29.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如下图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
30.三角形ABC和三角形DEF是两个完全一样的等腰直角三角形,求阴影部分面积。(单位:m)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.S=(a+b)×h÷2
【分析】根据梯形面积公式:梯形面积=(上底+下底)×高÷2,将对应的字母一个一个代入写出公式即可。
【详解】由分析可得:
梯形面积=(上底+下底)×高÷2,用字母表示为:S=(a+b)×h÷2
【点睛】本题考查了用字母表示梯形面积公式,牢记公式是解题的关键。
2.22dm2
【分析】已知梯形的下底是上底的1.2倍,先用上底乘1.2,求出梯形的下底;再根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个梯形的面积。
【详解】下底:5×1.2=6(dm)
梯形的面积:
(5+6)×4÷2
=11×4÷2
=44÷2
=22(dm2)
这个梯形的面积是22dm2。
【点睛】先根据乘法的意义求出下底,再根据梯形的面积公式求解。
3. 上底+下底 高 (上底+下底)×高÷2
【分析】两个完全一样的梯形,梯形面积相等,2S梯形=S平行四边形,梯形的上下底之和等于平行四边形的底边长度,梯形的高等于平行四边形的高,由平行四边形的面积公式代换为梯形的上下底和高,即可推导出梯形的面积计算公式。
【详解】如图所示:
则两个完全一样的梯形可以拼成一个平行四边形,拼成的平行四边形的底等于梯形的上底+下底,高等于梯形的高。由平行四边形面积=底×高,可推出梯形面积=(上底+下底)×高÷2。
【点睛】掌握梯形的面积推导过程是解答题目的关键。
4.25
【分析】如图,,将梯形面积转化为涂色平行四边形的面积。平行四边形的底是6+4=10(cm),高是2.5cm,面积是10×2.5=25(cm2),所以梯形的面积是25cm2。
【详解】(6+4)×2.5
=10×2.5
=25(cm2)
所以,梯形的面积是25cm2。
【点睛】本题考查用转化法求梯形面积的计算,有一定观察力,熟记“平行四边形面积=底×高”是解题的关键。
5.40
【分析】根据题意,结合梯形的面积公式:可知,梯形的面积等于和它等底等高的平行四边形面积的一半。
【详解】80÷2=40()
所以每个梯形的面积是40。
【点睛】此题考查了梯形的面积公式。要求熟练掌握并灵活运用。
6. 52 36
【分析】先求出梯形下底的长,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式求出这个梯形的面积;在这个梯形中画一个最大的三角形,三角形的底等于梯形的下底,三角形的高等于梯形的高,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】4+5=9(dm)
(4+9)×8÷2
=13×8÷2
=104÷2
=52(dm2)
9×8÷2
=72÷2
=36(dm2)
所以,梯形的面积是52 dm2,这个三角形的面积是36 dm2。
【点睛】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
7.240
【分析】根据梯形的面积公式:S=(a+b)h÷2,据此求出装饰板一面的面积,再用一面的面积乘2即可求出涂油漆的面积。
【详解】1.2米=12分米
(9+11)×12÷2×2
=20×12÷2×2
=240÷2×2
=120×2
=240(平方分米)
则涂油漆的面积是240平方分米。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
8.C
【分析】根据“平行线间的所有垂线段相等”可知,这三个图形的高都相等。可以设它们的高为1,然后根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算,分别求出它们的面积,再比较,即可得出结论。
【详解】设平行四边形、三角形、梯形的高都是1;
平行四边形的面积:5×1=5
三角形的面积:10×1÷2=5
梯形的面积:
(2+8)×1÷2
=10×1÷2
=5
平行四边形、三角形和梯形的面积相比较,一样大。
故答案为:C
【点睛】利用赋值法,运用平行四边形、三角形、梯形的面积公式,直接计算出结果,再比较,更直观。
9.C
【分析】根据题意,最上层有1根,最下层有8根,相邻两层相差1根,这堆钢管的层数是(8-1+1)层,根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可求出这堆钢管的数量,据此解答。
【详解】(1+8)×(8-1+1)÷2
=9×8÷2
=72÷2
=36(根)
一堆钢管,最下层有8根,最上层有1根,每相邻两层相差1根,这堆钢管共有36根。
故答案为:C
【点睛】解答此题的关键的确定这堆钢管的层数,然后再根据梯形的面积公式进行计算即可。
10.A
【分析】沿平行四边形钝角所在的一个顶点,向对边作垂线,这样的高有两条,沿这两条高剪开,都能得到一个三角形和一个梯形;或得到两个梯形且是直角梯形;如果平行四边形的高的两个端点刚好是平行四边形的两个顶点,则将一个平行四边形沿高剪开,可能得到两个三角形,据此画图解答。
【详解】
由以上图形可以看出,将一个平行四边形沿高剪开,可能得到一个三角形和一个梯形、两个梯形或两个三角形,不可能得到一个平行四边形和一个梯形。
故答案为:A
【点睛】本题考查了平行四边形、三角形和梯形的认识以及平行四边形的拼接。
11.C
【分析】平行四边形的两组对边是平行的,它的高有无数条,且都是相等的,据此对该题进行判断即可。
【详解】由分析可得:
由于平行四边形的高有无数条且都是相等的,把平行四边形任意分割成两个梯形,这两个梯形的高还是等于原来平行四边形的高,所以这两个梯形的高总是相等的。
故答案为:C
【点睛】本题考查了对平行四边形的认识和特征的掌握,明确分割后的梯形的高就是该平行四边形的高为解题的关键。
12.A
【分析】从图中可知,梯形的面积+三角形的面积=长方形的面积,根据长方形的面积=长×宽,由此求出梯形的面积与三角形的面积之和;又已知梯形的面积比三角形的面积大30cm2,根据和差问题公式:(和+差)÷2=较大数,求出梯形的面积;最后根据梯形的上底=梯形的面积×2÷高-下底,代入数据计算,即可求出梯形的上底。
【详解】长方形的面积:
15×10=150(cm2)
梯形的面积:
(150+30)÷2
=180÷2
=90(cm2)
梯形的上底:
90×2÷10-15
=18-15
=3(cm)
梯形的上底是3cm。
故答案为:A
【点睛】关键是从图中分析出梯形、三角形、长方形面积之间的关系,再利用和差问题的解题方法解答。
13.C
【分析】由图形可知,用篱笆的长度减去20米即可得到梯形的上底与下底的和,再根据梯形的面积公式:S=(a+b)×h÷2,据此进行计算即可。
【详解】(65-20)×20÷2
=45×20÷2
=900÷2
=450(平方米)
则这个养鸡场占地面积是450平方米。
故答案为:C
【点睛】本题考查梯形的面积,求出梯形的上底与下底的和是解题的关键。
14.C
【分析】如图所示,三角形ABC的面积=AB×高1÷2,三角形ABD的面积=AB×高2÷2,根据梯形的特征,高1和高2相等,所以三角形ABC的面积和三角形ABD的面积相等,据此解答。
【详解】三角形ABC的面积=AB×高1÷2,
三角形ABD的面积=AB×高2÷2,
因为上底AB与下底CD平行,所以高1=高2
所以三角形ABC的面积=三角形ABD的面积,即S①+S③=S③+S②,因此S①=S②。
故答案为:C
【点睛】解答本题的关键是掌握梯形的特征、梯形的面积计算公式进行求解。
15.A
【分析】根据题意可知,一个梯形,下底是6厘米,如果上底增加3厘米,就变成一个正方形,那么原来梯形的高是6厘米,上底是(6-3)厘米,根据梯形的面积公式把数据代入公式解答。
【详解】6-3=3(厘米)
(3+6)×6÷2
=9×6÷2
=27(平方厘米)
即这个梯形的面积是27平方厘米。
故答案为:A
【点睛】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
16.B
【分析】根据题意可知,圆木一共有5层,利用堆成梯形的物品的计算方法:根数=(上层根数+下层根数)×层数÷2,代入数据求出这堆圆木的根数,据此解答。
【详解】(12+6)×5÷2
=18×5÷2
=45(根)
这堆圆木共有45根。
故答案为:B
【点睛】本题的关键是根据堆成梯形物品的计算方法求出圆木的根数。
17.×
【分析】积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
根据梯形的面积=(上底+下底)×高÷2以及积的变化规律可知,一个梯形的上底、下底都乘2,那么它的上、下底之和乘2,则面积也乘2;梯形的高乘2,则面积乘2;最终面积扩大到原来的(2×2)倍。可以举例说明。
【详解】如:设原来梯形的上底是2、下底是4、高是10;
原来梯形的面积:
(2+4)×10÷2
=6×10÷2
=30
梯形的上底、下底和高都乘2,现在梯形的面积:
(2×2+4×2)×(10×2)÷2
=(4+8)×20÷2
=12×20÷2
=120
面积扩大到原来的:120÷30=4
所以,一个梯形的上底、下底和高都乘2,面积就扩大到原来的4倍。
原题说法错误。
故答案为:×
【点睛】本题考查梯形面积公式以及积的变化规律的应用,举例说明更直观。
18.×
【分析】沿着一个梯形的上底中点和下底中点画一条直线,把这个梯形分成两个小梯形,这两个小梯形的上下底之和相等,高相等,根据梯形的面积公式:S=(a+b) × h÷2,所以它们的面积就相等,但是这两个小梯形的形状不一定相同。也就是两条腰长不一定相等,所以它们的周长不一定相等。据此解答。
【详解】如图所示:
这2个小梯形的面积相等,形状不一定相同,所以它们的周长不一定相等。
故答案为:×
【点睛】此题的解题关键是掌握梯形的周长、面积的计算方法以及梯形的特点。
19.×
【分析】平行四边形,是在同一个二维平面内,由两组平行线段组成的闭合图形。只有一组对边平行的四边形叫做梯形;据此解答。
【详解】两个等底等高的平行四边形,不能拼成梯形,如图:
上面的两个平行四边形等底等高,但它们是不可以拼成梯形的。
故答案为:×
【点睛】本题主要考查学生对平行四边形、梯形的认识。
20.×
【分析】梯形的面积=(上底+下底)×高÷2,据此举例说明即可。
【详解】假设梯形上底5cm,下底8cm,高4cm
(5+8)×4÷2
=13×4÷2
=26(cm2)
上底减少2cm,高增加2cm,上底变成3cm,高变成6cm
(3+8)×6÷2
=11×6÷2
=33(cm2)
面积变了,所以原题说法错误。
故答案为:×
【点睛】关键是掌握并灵活运用梯形面积公式。
21.√
【分析】只有一组对边平行的四边形叫做梯形;有一个角是直角的梯形叫做直角梯形。
有两组对边分别平行且相等的四边形,叫做平行四边形。
【详解】如图:
两个一样的直角梯形,可以拼成一个平行四边形。
原题说法正确。
故答案为:√
【点睛】本题考查根据直角梯形、平行四边形的特点进行图形的拼组。
22.17.5平方米;33.84平方厘米;270平方厘米
【分析】根据梯形的面积=(上底+下底)×高÷2,代入数据解答。
【详解】(4+3)×5÷2
=7×5÷2
=17.5(平方米)
第一个梯形的面积是17.5平方米。
(8.2+5.9)×4.8÷2
=14.1×4.8÷2
=33.84(平方厘米)
第二个梯形的面积是33.84平方厘米。
(12+15)×20÷2
=27×20÷2
=270(平方厘米)
第三个梯形的面积是270平方厘米。
23.10平方厘米
【分析】三角形面积=底×高÷2,据此列式求出三角形ABD的面积。将梯形的面积减去三角形ABD的面积,即可求出阴影部分的面积。
【详解】4×4÷2=8(平方厘米)
18-8=10(平方厘米)
所以,阴影部分的面积是10平方厘米。
24.75平方厘米
【分析】如果上底延长5厘米,那么这个直角梯形就多出一个与它等高的三角形,三角形的底是5厘米,可利用“三角形的面积=底×高÷2”计算出直角梯形的高,直角梯形与增加的三角形组成了一个正方形,可用正方形的面积减去三角形的面积即可得到答案。
【详解】25×2÷5
=50÷5
=10(厘米)
10×10-25
=100-25
=75(平方厘米)
答:梯形原来的面积是75平方厘米。
【点睛】解答此题的关键是根据增加的长度和面积确定直角梯形的高,然后再列式计算。
25.1200平方米
【分析】梯形面积=(上底+下底)×高÷2,长方形面积=长×宽,据此分别求出梯形和长方形的面积,再将梯形面积减去长方形面积,即可求出草地的面积。
【详解】(40+70)×30÷2-30×15
=110×30÷2-450
=1650-450
=1200(平方米)
答:草地的面积是1200平方米。
【点睛】本题考查了梯形和长方形的面积,熟记面积公式是解题的关键。
26.690平方米
【分析】观察图形可知,篱笆的长度是由上底、下底和30米组成的,已知篱笆长76米,则用(76-30)即可求出上底跟下底的和,然后根据梯形的面积公式即可求解。
【详解】(76-30)×30÷2
=46×30÷2
=1380÷2
=690(平方米)
答:这个菜园的面积是690平方米。
【点睛】本题考查了梯形面积的实际应用,要熟练掌握相关公式。
27.53.6平方厘米
【分析】根据题意,一个直角梯形的上底是5.4厘米,如果把上底增加2.6厘米,它就变成了一个正方形,根据正方形的特征可知,直角梯形的下底、高都是(5.4+2.6)厘米;根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个梯形的面积。
【详解】(5.4+5.4+2.6)×(5.4+2.6)÷2
=13.4×8÷2
=107.2÷2
=53.6(平方厘米)
答:这个梯形的面积是53.6平方厘米。
【点睛】本题考查梯形面积公式的运用,利用正方形的特征确定梯形的下底和高是解题的关键。
28.60000千克;60吨
【分析】已知梯形菜地的上底、下底和高,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出这块地的面积;
再用平均每平方米可收白菜的质量乘这块地的面积,求出这块地收白菜的总质量;最后根据进率“1吨=1000千克”换算单位即可。
【详解】(32+48)×60÷2
=80×60÷2
=4800÷2
=2400(平方米)
25×2400=60000(千克)
60000千克=60吨
答:这块地共收割白菜60000千克,合60吨。
【点睛】本题考查梯形面积公式的实际应用以及质量单位的换算。
29.21平方米
【分析】这块地的形状是梯形,梯形的上底是(3.6+2.6)米,梯形的下底是(2.2+2.6+3)米,梯形的高是3米。梯形的面积=(上底+下底)×高÷2,把梯形上底、下底、高的数值代入公式计算即可求出这块地的面积。
【详解】上底:3.6+2.6=6.2(米)
下底:2.2+2.6+3
=4.8+3
=7.8(米)
面积:(6.2+7.8)×3÷2
=14×3÷2
=42÷2
=21(平方米)
答:这块地的面积共有21平方米。
【点睛】此题主要考查了梯形面积计算公式的应用。计算梯形的面积时,不要忘记除以2。
30.102平方米
【分析】因为三角形ABC和三角形DEF是两个完全一样的等腰直角三角形,所以DE=EF=20米,MB=BF=EF-BE=20-6=14米,阴影部分面积=S△ABC-S△MBF,梯形DEBM的面积=S△DEF-S△MBF,则阴影部分面积=梯形DEBM的面积=(上底+下底)×高÷2,据此解答。
【详解】20-6=14(米)
(14+20)×6÷2
=34×6÷2
=204÷2
=102(平方米)
答:阴影部分面积是102平方米。
【点睛】此题的解题关键是把求阴影部分面积转化成求梯形的面积,然后利用面积公式求出即可。
答案第1页,共2页
答案第1页,共2页
人教版 五年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.如果用S表示梯形的面积,用a、b和h分别表示梯形的上底、下底和高,那么梯形的面积公式是( )。
2.一个梯形的上底是5dm,下底是上底的1.2倍,高是4dm,这个梯形的面积是( )。
3.两个完全一样的梯形可以拼成一个平行四边形,拼成的平行四边形的底等于梯形的( ),高等于梯形的( )。由平行四边形面积=底×高,可推出梯形面积=( )。
4.我国古代数学家刘徽利用出入相补原理来计算平面图形的面积。把一个梯形沿着两腰中点的连线剪开,旋转后拼成了一个平行四边形(如图)。原图中梯形的面积是( )平方厘米。
5.两个完全一样的梯形拼成一个平行四边形,如果这个平行四边形的面积是80,那么每个梯形的面积是( )。
6.一张梯形纸片的上底是4dm,下底比上底长5dm,高是8dm,面积是( )dm2,如果从中剪去一个最大的三角形,这个三角形的面积是( )dm2。
7.一个梯形的装饰板,上底9分米,下底11分米,高1.2米,两面都要涂油漆,涂油漆的面积是( )平方分米。
二、选择题
8.如图,在平行线之间有三个图形,它们的面积相比较,( )。
A.平行四边形的面积最大 B.三角形面积最大 C.一样大
9.一堆钢管,最下层有8根,最上层有1根,每相邻两层相差1根,这堆钢管共有( )根。
A.72 B.32 C.36
10.将一个平行四边形沿高剪开,不可能得到( )。
A.一个平行四边形和一个梯形 B.两个三角形 C.两个梯形
11.把一个平行四边形任意分割成两个梯形,这两个梯形的( )总是相等的。
A.面积 B.周长 C.高
12.如图所示,把一个长方形分成一个梯形和一个三角形。已知梯形的面积比三角形的面积大30cm2,那么梯形的上底是( )。
A.3cm B.4cm C.5cm
13.用65米的篱笆靠端墙围城一个梯形的养鸡场(如图),这个养鸡场占地面积是( )平方米。
A.1320 B.880 C.450
14.如图:梯形内有①、②两个三角形,则①、②两个三角形的面积关系是( )。
A.S①>S② B.S①<S② C.S①=S②
15.一个梯形的上底增加3厘米后就变成一个边长6厘米的正方形,这个梯形的面积是( )平方厘米。
A.27 B.36 C.48
16.一堆大小相同的圆木,堆成梯形形状,最下层有12根,最上层有6根,共堆了5层,这堆圆木共有( )。
A.51根 B.45根 C.66根
三、判断题
17.一个梯形的上底、下底和高都乘2,面积就扩大到原来的2倍。( )
18.连接梯形上底和下底的中点,把它分成2个小梯形,它们的周长相等。( )
19.两个等底等高的平行四边形一定可以拼成一个梯形。( )
20.梯形的上底减少2cm,高增加2cm,它的面积不变。( )
21.两个一样的直角梯形,可以拼成一个平行四边形。( )
四、计算下面每个梯形的面积
22.
五、解答题
23.如下图,面积为18平方厘米的直角梯形ABCD被对角线分成两个三角形,其中三角形ABD为等腰直角三角形。已知AB=4厘米,求阴影部分的面积。
24.小明计算一个梯形面积的时候发现,如果把这个梯形的上底增加5厘米,梯形的面积就增加了25平方厘米,且变成一个正方形,请你计算一下梯形原来的面积是多少?
25.在一块上底为40米,下底为70米,高为30米的梯形草地中间有一个长为30米,宽为15米的长方形游泳池,如图。草地的面积是多少平方米?
26.靠墙边围成一个菜园,围菜园的篱笆长76米,求这个菜园的面积。
27.一个直角梯形的上底是5.4厘米,如果把上底增加2.6厘米,它就变成了一个正方形。这个梯形的面积是多少平方厘米?
28.一块梯形的菜地,上底是32米,下底是48米,高是60米,如果平均每平方米可收白菜25千克,这块地共收割白菜多少千克?合多少吨?
29.金湾区某学校开始劳动教育课程,规划了一块实践基地,形状如下图所示,分别种了白萝卜、洋葱和黄瓜,求这块地的面积共有多少平方米?
30.三角形ABC和三角形DEF是两个完全一样的等腰直角三角形,求阴影部分面积。(单位:m)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.S=(a+b)×h÷2
【分析】根据梯形面积公式:梯形面积=(上底+下底)×高÷2,将对应的字母一个一个代入写出公式即可。
【详解】由分析可得:
梯形面积=(上底+下底)×高÷2,用字母表示为:S=(a+b)×h÷2
【点睛】本题考查了用字母表示梯形面积公式,牢记公式是解题的关键。
2.22dm2
【分析】已知梯形的下底是上底的1.2倍,先用上底乘1.2,求出梯形的下底;再根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个梯形的面积。
【详解】下底:5×1.2=6(dm)
梯形的面积:
(5+6)×4÷2
=11×4÷2
=44÷2
=22(dm2)
这个梯形的面积是22dm2。
【点睛】先根据乘法的意义求出下底,再根据梯形的面积公式求解。
3. 上底+下底 高 (上底+下底)×高÷2
【分析】两个完全一样的梯形,梯形面积相等,2S梯形=S平行四边形,梯形的上下底之和等于平行四边形的底边长度,梯形的高等于平行四边形的高,由平行四边形的面积公式代换为梯形的上下底和高,即可推导出梯形的面积计算公式。
【详解】如图所示:
则两个完全一样的梯形可以拼成一个平行四边形,拼成的平行四边形的底等于梯形的上底+下底,高等于梯形的高。由平行四边形面积=底×高,可推出梯形面积=(上底+下底)×高÷2。
【点睛】掌握梯形的面积推导过程是解答题目的关键。
4.25
【分析】如图,,将梯形面积转化为涂色平行四边形的面积。平行四边形的底是6+4=10(cm),高是2.5cm,面积是10×2.5=25(cm2),所以梯形的面积是25cm2。
【详解】(6+4)×2.5
=10×2.5
=25(cm2)
所以,梯形的面积是25cm2。
【点睛】本题考查用转化法求梯形面积的计算,有一定观察力,熟记“平行四边形面积=底×高”是解题的关键。
5.40
【分析】根据题意,结合梯形的面积公式:可知,梯形的面积等于和它等底等高的平行四边形面积的一半。
【详解】80÷2=40()
所以每个梯形的面积是40。
【点睛】此题考查了梯形的面积公式。要求熟练掌握并灵活运用。
6. 52 36
【分析】先求出梯形下底的长,根据梯形的面积公式:S=(a+b)h÷2,把数据代入公式求出这个梯形的面积;在这个梯形中画一个最大的三角形,三角形的底等于梯形的下底,三角形的高等于梯形的高,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【详解】4+5=9(dm)
(4+9)×8÷2
=13×8÷2
=104÷2
=52(dm2)
9×8÷2
=72÷2
=36(dm2)
所以,梯形的面积是52 dm2,这个三角形的面积是36 dm2。
【点睛】此题主要考查梯形、三角形面积公式的灵活运用,关键是熟记公式。
7.240
【分析】根据梯形的面积公式:S=(a+b)h÷2,据此求出装饰板一面的面积,再用一面的面积乘2即可求出涂油漆的面积。
【详解】1.2米=12分米
(9+11)×12÷2×2
=20×12÷2×2
=240÷2×2
=120×2
=240(平方分米)
则涂油漆的面积是240平方分米。
【点睛】本题考查梯形的面积,熟记公式是解题的关键。
8.C
【分析】根据“平行线间的所有垂线段相等”可知,这三个图形的高都相等。可以设它们的高为1,然后根据平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,代入数据计算,分别求出它们的面积,再比较,即可得出结论。
【详解】设平行四边形、三角形、梯形的高都是1;
平行四边形的面积:5×1=5
三角形的面积:10×1÷2=5
梯形的面积:
(2+8)×1÷2
=10×1÷2
=5
平行四边形、三角形和梯形的面积相比较,一样大。
故答案为:C
【点睛】利用赋值法,运用平行四边形、三角形、梯形的面积公式,直接计算出结果,再比较,更直观。
9.C
【分析】根据题意,最上层有1根,最下层有8根,相邻两层相差1根,这堆钢管的层数是(8-1+1)层,根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可求出这堆钢管的数量,据此解答。
【详解】(1+8)×(8-1+1)÷2
=9×8÷2
=72÷2
=36(根)
一堆钢管,最下层有8根,最上层有1根,每相邻两层相差1根,这堆钢管共有36根。
故答案为:C
【点睛】解答此题的关键的确定这堆钢管的层数,然后再根据梯形的面积公式进行计算即可。
10.A
【分析】沿平行四边形钝角所在的一个顶点,向对边作垂线,这样的高有两条,沿这两条高剪开,都能得到一个三角形和一个梯形;或得到两个梯形且是直角梯形;如果平行四边形的高的两个端点刚好是平行四边形的两个顶点,则将一个平行四边形沿高剪开,可能得到两个三角形,据此画图解答。
【详解】
由以上图形可以看出,将一个平行四边形沿高剪开,可能得到一个三角形和一个梯形、两个梯形或两个三角形,不可能得到一个平行四边形和一个梯形。
故答案为:A
【点睛】本题考查了平行四边形、三角形和梯形的认识以及平行四边形的拼接。
11.C
【分析】平行四边形的两组对边是平行的,它的高有无数条,且都是相等的,据此对该题进行判断即可。
【详解】由分析可得:
由于平行四边形的高有无数条且都是相等的,把平行四边形任意分割成两个梯形,这两个梯形的高还是等于原来平行四边形的高,所以这两个梯形的高总是相等的。
故答案为:C
【点睛】本题考查了对平行四边形的认识和特征的掌握,明确分割后的梯形的高就是该平行四边形的高为解题的关键。
12.A
【分析】从图中可知,梯形的面积+三角形的面积=长方形的面积,根据长方形的面积=长×宽,由此求出梯形的面积与三角形的面积之和;又已知梯形的面积比三角形的面积大30cm2,根据和差问题公式:(和+差)÷2=较大数,求出梯形的面积;最后根据梯形的上底=梯形的面积×2÷高-下底,代入数据计算,即可求出梯形的上底。
【详解】长方形的面积:
15×10=150(cm2)
梯形的面积:
(150+30)÷2
=180÷2
=90(cm2)
梯形的上底:
90×2÷10-15
=18-15
=3(cm)
梯形的上底是3cm。
故答案为:A
【点睛】关键是从图中分析出梯形、三角形、长方形面积之间的关系,再利用和差问题的解题方法解答。
13.C
【分析】由图形可知,用篱笆的长度减去20米即可得到梯形的上底与下底的和,再根据梯形的面积公式:S=(a+b)×h÷2,据此进行计算即可。
【详解】(65-20)×20÷2
=45×20÷2
=900÷2
=450(平方米)
则这个养鸡场占地面积是450平方米。
故答案为:C
【点睛】本题考查梯形的面积,求出梯形的上底与下底的和是解题的关键。
14.C
【分析】如图所示,三角形ABC的面积=AB×高1÷2,三角形ABD的面积=AB×高2÷2,根据梯形的特征,高1和高2相等,所以三角形ABC的面积和三角形ABD的面积相等,据此解答。
【详解】三角形ABC的面积=AB×高1÷2,
三角形ABD的面积=AB×高2÷2,
因为上底AB与下底CD平行,所以高1=高2
所以三角形ABC的面积=三角形ABD的面积,即S①+S③=S③+S②,因此S①=S②。
故答案为:C
【点睛】解答本题的关键是掌握梯形的特征、梯形的面积计算公式进行求解。
15.A
【分析】根据题意可知,一个梯形,下底是6厘米,如果上底增加3厘米,就变成一个正方形,那么原来梯形的高是6厘米,上底是(6-3)厘米,根据梯形的面积公式把数据代入公式解答。
【详解】6-3=3(厘米)
(3+6)×6÷2
=9×6÷2
=27(平方厘米)
即这个梯形的面积是27平方厘米。
故答案为:A
【点睛】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
16.B
【分析】根据题意可知,圆木一共有5层,利用堆成梯形的物品的计算方法:根数=(上层根数+下层根数)×层数÷2,代入数据求出这堆圆木的根数,据此解答。
【详解】(12+6)×5÷2
=18×5÷2
=45(根)
这堆圆木共有45根。
故答案为:B
【点睛】本题的关键是根据堆成梯形物品的计算方法求出圆木的根数。
17.×
【分析】积的变化规律:一个因数不变,另一个因数乘几或除以几(0除外),积也乘(或除以)几。
根据梯形的面积=(上底+下底)×高÷2以及积的变化规律可知,一个梯形的上底、下底都乘2,那么它的上、下底之和乘2,则面积也乘2;梯形的高乘2,则面积乘2;最终面积扩大到原来的(2×2)倍。可以举例说明。
【详解】如:设原来梯形的上底是2、下底是4、高是10;
原来梯形的面积:
(2+4)×10÷2
=6×10÷2
=30
梯形的上底、下底和高都乘2,现在梯形的面积:
(2×2+4×2)×(10×2)÷2
=(4+8)×20÷2
=12×20÷2
=120
面积扩大到原来的:120÷30=4
所以,一个梯形的上底、下底和高都乘2,面积就扩大到原来的4倍。
原题说法错误。
故答案为:×
【点睛】本题考查梯形面积公式以及积的变化规律的应用,举例说明更直观。
18.×
【分析】沿着一个梯形的上底中点和下底中点画一条直线,把这个梯形分成两个小梯形,这两个小梯形的上下底之和相等,高相等,根据梯形的面积公式:S=(a+b) × h÷2,所以它们的面积就相等,但是这两个小梯形的形状不一定相同。也就是两条腰长不一定相等,所以它们的周长不一定相等。据此解答。
【详解】如图所示:
这2个小梯形的面积相等,形状不一定相同,所以它们的周长不一定相等。
故答案为:×
【点睛】此题的解题关键是掌握梯形的周长、面积的计算方法以及梯形的特点。
19.×
【分析】平行四边形,是在同一个二维平面内,由两组平行线段组成的闭合图形。只有一组对边平行的四边形叫做梯形;据此解答。
【详解】两个等底等高的平行四边形,不能拼成梯形,如图:
上面的两个平行四边形等底等高,但它们是不可以拼成梯形的。
故答案为:×
【点睛】本题主要考查学生对平行四边形、梯形的认识。
20.×
【分析】梯形的面积=(上底+下底)×高÷2,据此举例说明即可。
【详解】假设梯形上底5cm,下底8cm,高4cm
(5+8)×4÷2
=13×4÷2
=26(cm2)
上底减少2cm,高增加2cm,上底变成3cm,高变成6cm
(3+8)×6÷2
=11×6÷2
=33(cm2)
面积变了,所以原题说法错误。
故答案为:×
【点睛】关键是掌握并灵活运用梯形面积公式。
21.√
【分析】只有一组对边平行的四边形叫做梯形;有一个角是直角的梯形叫做直角梯形。
有两组对边分别平行且相等的四边形,叫做平行四边形。
【详解】如图:
两个一样的直角梯形,可以拼成一个平行四边形。
原题说法正确。
故答案为:√
【点睛】本题考查根据直角梯形、平行四边形的特点进行图形的拼组。
22.17.5平方米;33.84平方厘米;270平方厘米
【分析】根据梯形的面积=(上底+下底)×高÷2,代入数据解答。
【详解】(4+3)×5÷2
=7×5÷2
=17.5(平方米)
第一个梯形的面积是17.5平方米。
(8.2+5.9)×4.8÷2
=14.1×4.8÷2
=33.84(平方厘米)
第二个梯形的面积是33.84平方厘米。
(12+15)×20÷2
=27×20÷2
=270(平方厘米)
第三个梯形的面积是270平方厘米。
23.10平方厘米
【分析】三角形面积=底×高÷2,据此列式求出三角形ABD的面积。将梯形的面积减去三角形ABD的面积,即可求出阴影部分的面积。
【详解】4×4÷2=8(平方厘米)
18-8=10(平方厘米)
所以,阴影部分的面积是10平方厘米。
24.75平方厘米
【分析】如果上底延长5厘米,那么这个直角梯形就多出一个与它等高的三角形,三角形的底是5厘米,可利用“三角形的面积=底×高÷2”计算出直角梯形的高,直角梯形与增加的三角形组成了一个正方形,可用正方形的面积减去三角形的面积即可得到答案。
【详解】25×2÷5
=50÷5
=10(厘米)
10×10-25
=100-25
=75(平方厘米)
答:梯形原来的面积是75平方厘米。
【点睛】解答此题的关键是根据增加的长度和面积确定直角梯形的高,然后再列式计算。
25.1200平方米
【分析】梯形面积=(上底+下底)×高÷2,长方形面积=长×宽,据此分别求出梯形和长方形的面积,再将梯形面积减去长方形面积,即可求出草地的面积。
【详解】(40+70)×30÷2-30×15
=110×30÷2-450
=1650-450
=1200(平方米)
答:草地的面积是1200平方米。
【点睛】本题考查了梯形和长方形的面积,熟记面积公式是解题的关键。
26.690平方米
【分析】观察图形可知,篱笆的长度是由上底、下底和30米组成的,已知篱笆长76米,则用(76-30)即可求出上底跟下底的和,然后根据梯形的面积公式即可求解。
【详解】(76-30)×30÷2
=46×30÷2
=1380÷2
=690(平方米)
答:这个菜园的面积是690平方米。
【点睛】本题考查了梯形面积的实际应用,要熟练掌握相关公式。
27.53.6平方厘米
【分析】根据题意,一个直角梯形的上底是5.4厘米,如果把上底增加2.6厘米,它就变成了一个正方形,根据正方形的特征可知,直角梯形的下底、高都是(5.4+2.6)厘米;根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出这个梯形的面积。
【详解】(5.4+5.4+2.6)×(5.4+2.6)÷2
=13.4×8÷2
=107.2÷2
=53.6(平方厘米)
答:这个梯形的面积是53.6平方厘米。
【点睛】本题考查梯形面积公式的运用,利用正方形的特征确定梯形的下底和高是解题的关键。
28.60000千克;60吨
【分析】已知梯形菜地的上底、下底和高,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,求出这块地的面积;
再用平均每平方米可收白菜的质量乘这块地的面积,求出这块地收白菜的总质量;最后根据进率“1吨=1000千克”换算单位即可。
【详解】(32+48)×60÷2
=80×60÷2
=4800÷2
=2400(平方米)
25×2400=60000(千克)
60000千克=60吨
答:这块地共收割白菜60000千克,合60吨。
【点睛】本题考查梯形面积公式的实际应用以及质量单位的换算。
29.21平方米
【分析】这块地的形状是梯形,梯形的上底是(3.6+2.6)米,梯形的下底是(2.2+2.6+3)米,梯形的高是3米。梯形的面积=(上底+下底)×高÷2,把梯形上底、下底、高的数值代入公式计算即可求出这块地的面积。
【详解】上底:3.6+2.6=6.2(米)
下底:2.2+2.6+3
=4.8+3
=7.8(米)
面积:(6.2+7.8)×3÷2
=14×3÷2
=42÷2
=21(平方米)
答:这块地的面积共有21平方米。
【点睛】此题主要考查了梯形面积计算公式的应用。计算梯形的面积时,不要忘记除以2。
30.102平方米
【分析】因为三角形ABC和三角形DEF是两个完全一样的等腰直角三角形,所以DE=EF=20米,MB=BF=EF-BE=20-6=14米,阴影部分面积=S△ABC-S△MBF,梯形DEBM的面积=S△DEF-S△MBF,则阴影部分面积=梯形DEBM的面积=(上底+下底)×高÷2,据此解答。
【详解】20-6=14(米)
(14+20)×6÷2
=34×6÷2
=204÷2
=102(平方米)
答:阴影部分面积是102平方米。
【点睛】此题的解题关键是把求阴影部分面积转化成求梯形的面积,然后利用面积公式求出即可。
答案第1页,共2页
答案第1页,共2页
