6.多边形的面积——组合图形的面积同步练习(含解析)人教版五年级数学上册
文档属性
| 名称 | 6.多边形的面积——组合图形的面积同步练习(含解析)人教版五年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 457.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 15:14:31 | ||
图片预览




文档简介
6.多边形的面积——组合图形的面积同步练习 (含答案)
人教版 五年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.小美的父母计划购买一套公寓,小美想估计一下房屋的总面积(包括露台和墙,如户型图所示)。以下是小美测量的4种方式,你觉得这些方式都能估计出房屋的总面积吗?如果可以请在括号里打“√”,如果不可以请在括号里打“×”。
户型图 ( ) ( ) ( ) ( )
2.下图中每个小方格的面积表示1cm2,图1中涂色部分的面积是( )cm2,图2中图案的面积约是( )cm2。
图1 图2
3.如下图,平行四边形的面积是64cm2,则涂色部分的面积是( )cm2。
(第3题) (第4题)
4.如图所示,若阴影部分的面积是54cm2,则一个小正方形的面积是( )cm2。
5.陈燕从一个直角三角形纸板上剪下了一个正方形(如下图),剩下部分的面积是( )平方厘米。
6.小丽从一个上底为12.4厘米、下底为18.6厘米、高为4厘米的梯形卡纸中,剪掉一个最大的三角形,剩下卡纸的面积是( )平方厘米。
二、选择题
7.下图中这个精美的皮影人物的面积大约是( )平方厘米。(图中每个小方格的面积是4平方厘米)
A.24 B.96 C.60
8.有一个长方形,它的长减少5cm,面积就减少30cm2,剩下的部分正好是一个正方形。这个长方形的面积是( )cm2。
A.55 B.30 C.66
9.两个完全一样的直角三角形重叠成下图的形状,形成两个梯形,这两个梯形的面积相比。( )。
A.a大 B.b大 C.相等
10.把长2cm,宽1cm的长方形一层、二层、三层…有规律地摆下去(如图),摆到第十层时,这个图形的面积是( )cm2。
A.20 B.110 C.100
11.如图平行四边形中有①②③三个三角形,关于这三个三角形面积间的关系,下面的说法正确的是( )。
A.①>②+③ B.①<②+③ C.①=②+③
12.如图所示,是两个大小相同的正方形,正方形中的阴影部分哪一个面积更大?( )
A.甲大 B.乙大 C.一样大
13.图中A、B两点分别是长方形长和宽的中点,则阴影部分的面积是( )cm2。
A.32 B.18 C.16
14.比较下面阴影部分的面积,( )是错误的。
① ② ③ ④
A.图①中阴影部分的面积等于图②中阴影部分的面积
B.图②中阴影部分的面积等于图③中阴影部分的面积
C.图③中阴影部分的面积不等于图④中阴影部分的面积
三、判断题
15.长方形、三角形、平行四边形、正六边形都可以单独密铺。( )
16.不规则图形的面积可以转化为学过的图形来估算。( )
17.估算的面积一般比实际面积大。( )
18.如图,甲、乙两部分面积一样大。( )
19.求组合图形的面积,就是求几个简单图形的面积和. ( )
四、图形计算
20.求下图的面积。
21.下面是两个不同大小的正方形组合而成的图形,请你求出图中涂色部分的面积。(单位:厘米)
五、解答题
22.如下图,张叔叔准备在这块地里种白菜,如果每棵白菜占地0.25平方米,这块地能种多少棵白菜?
23.下图是一间房屋的侧面墙,如果用石灰粉刷这面墙,每平方米用石灰0.2千克,一共要用多少千克石灰?
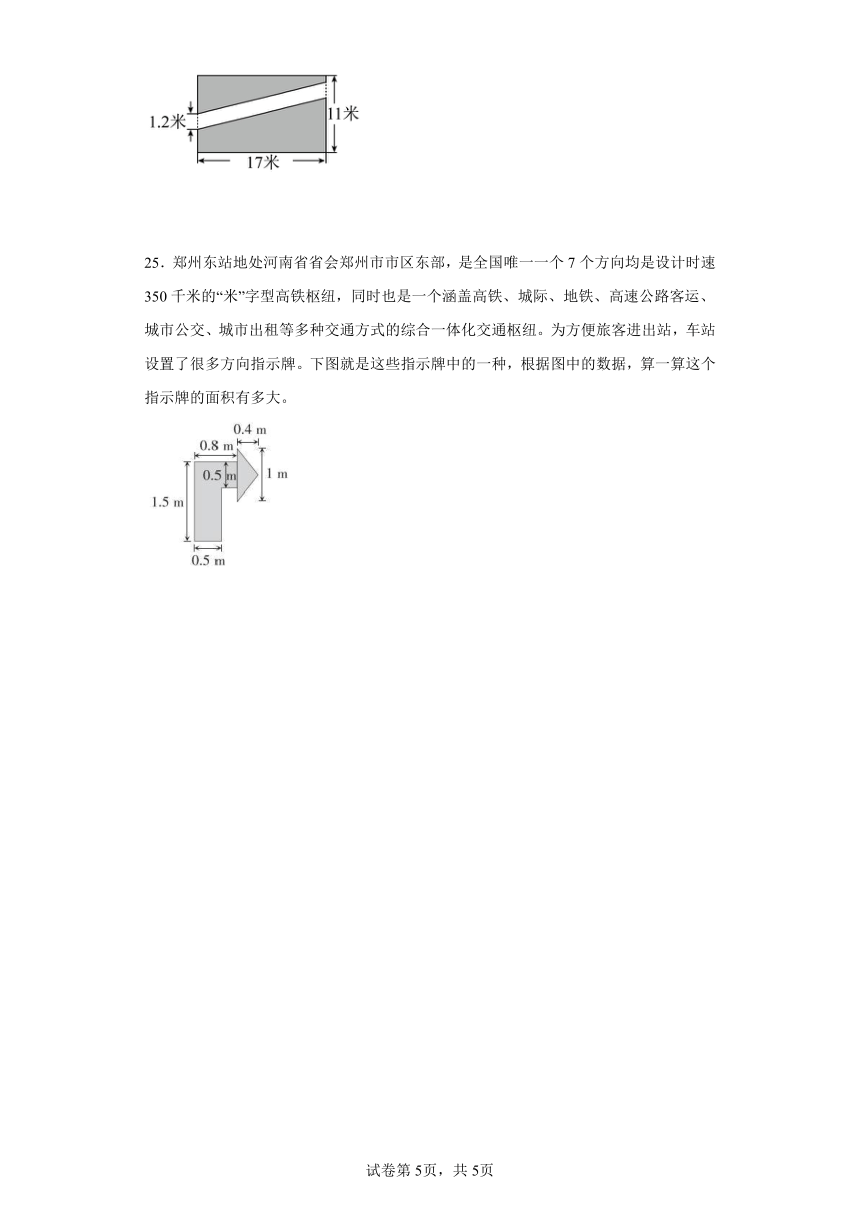
24.公园有一块长方形草地,长方形的长是17米,宽是11米,中间铺了一条石子路,那么,草地部分的面积有多大?
25.郑州东站地处河南省省会郑州市市区东部,是全国唯一一个7个方向均是设计时速350千米的“米”字型高铁枢纽,同时也是一个涵盖高铁、城际、地铁、高速公路客运、城市公交、城市出租等多种交通方式的综合一体化交通枢纽。为方便旅客进出站,车站设置了很多方向指示牌。下图就是这些指示牌中的一种,根据图中的数据,算一算这个指示牌的面积有多大。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. √ √ √ √
【分析】这个户型图是一个不规则图形,可以运用分割法或添补法把图形分成几个规则图形,分别量出需要的数据计算出它们的面积,再把各图形的面积相加即可求出房屋的总面积。
【详解】如下图所示,图1把图形分割成两个长方形,下面的长方形测量出了长和宽,上面的长方形长已知,宽可以计算出来,根据长方形的面积=长×宽,可以分别求出它们的面积,再把它们的面积相加即可;图2同样分成两个长方形,长方形的长和宽通过测量或计算都可以得到,则可以求出面积,继而求出房屋的总面积;图3添补成一个长方形,可以用整个长方形的面积减去右上角的小长方形的面积,即可求出房屋的总面积;图4左边的长方形测量了长和宽,右边的小长方形通过计算可以得到长,宽以测量出来,则可以求出各长方形的面积,继而求出房屋的总面积。
所以,这4种测量方式都能估计出房屋的总面积,括号里面都应打“√”。
【点睛】本题考查组合图形的面积。运用分割法或添补法把图形分成几个规则图形是解题的关键。
2. 6.5 4
【分析】不规则图形的面积估算方法:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是不规则图形的格子数,最后乘每个小方格的面积即可。
【详解】(1)满格有4个,不满格有5个;
一共有:
4+5÷2
=4+2.5
=6.5(个)
面积:1×6.5=6.5(cm2)
图1中涂色部分的面积是6.5cm2。
(2)只有不满格的,有8个;
一共有:8÷2=4(个)
面积:1×4=4(cm2)
图2中图案的面积约是4cm2。
【点睛】掌握不规则图形面积的估算方法是解题的关键。
3.32
【分析】观察图形可知,涂色部分是两个三角形的和,两个三角形的底的和等于平行四边形的底,三角形的高等于平行四边形的高;根据三角形面积公式:面积=底×高÷2;平行四边形面积公式:面积=底×高;由此可知,涂色部分的面积等于平行四边形面积的一半;即平行四边形面积÷2=涂色部分的面积,据此求出涂色部分的面积。
【详解】64÷2=32(cm2)
即涂色部分的面积是32cm2。
【点睛】解答本题的关键明确阴影部分的底的和与平行四边形的底的关系,阴影部分的高与平行四边形的高之间的关系是解答本题的关键。
4.9
【分析】数一数涂色部分的面积一共是由6个小正方形组成的,所以用涂色部分的面积除以正方形的个数即可求出一个小正方形的面积。
【详解】54÷6=9(cm2)
即一个小正方形的面积是9cm2。
【点睛】此题的解题关键是通过转化的数学思想,把阴影部分的面积转化成正方形的面积。
5.24
【分析】通过旋转,可将阴影部分变化为如下图:
阴影部分相当于一个底为8厘米,高为6厘米的直角三角形,根据三角形的面积=底×高÷2,用8×6÷2即可求出阴影部分的面积。
【详解】8×6÷2=24(平方厘米)
剩下部分的面积是24平方厘米。
【点睛】解答本题的关键是学会转化阴影部分的面积,将其变成容易计算的图形。
6.24.8
【分析】要想在这个梯形卡纸中剪去一个最大的三角形,必须把梯形的下底作为三角形的底。把梯形的高作为三角形的高,则剩下的图形的面积就是以梯形的上底为底,梯形的高为高的三角形的面积,据此利用三角形的面积公式计算即可解答。
【详解】12.4×4÷2=24.8(平方厘米)
即剩下卡纸的面积是24.8平方厘米。
【点睛】此题考查组合图形的面积,解决此题关键是弄明白怎么剪才能使三角形的面积最大,进而得出剩下的是以上底为底边的三角形的面积。
7.C
【分析】用数小方格的方法估算不规则图形的面积,通常是先数整格数,再数不足格数,整格数按一个面积单位计算,不足格的按半个面积单位计算。
【详解】观察图形可知,不足格大概有26个。
26÷2=13
13×4=52(平方厘米)
52比较接近60,所以这个精美的皮影人物的面积大约是60平方厘米。
故答案为:C
【点睛】用数小方格的方法估算不规则图形的面积,通常是先数整格数,再数不足格数,整格数按一个面积单位计算,不足格的按半个面积单位计算。注意:数格是按一定的顺序数,既不要重复,也不要遗漏。
8.C
【分析】由题意得:长方形的长减去5cm等于长方形的宽。根据长方形面积=长×宽,算出长方形的宽,因为剩下的部分正好是一个正方形,那么剩下的正方形的边长为6,则可以算出长方形的长,再计算长方形的面积即可。
【详解】长方形的宽:305=6(cm)
长方形的长:65=11(cm)
长方形的面积:11 6=66(cm2)
故答案为:C
【点睛】本题考查了长方形以及正方形的知识点。掌握长方形和正方形的特征以及面积公式是关键。
9.C
【分析】从图中可知,一个直角三角形是由梯形a和空白小三角形组成,另一个直角三角形是由梯形b和空白小三角形组成,因为两个直角三角形完全一样,它们的面积相等,空白小三角形是公共部分,由此得出梯形a和b的面积关系。
【详解】梯形a的面积+空白小三角形的面积=梯形b的面积+空白小三角形的面积
所以梯形a的面积=梯形b的面积
故答案为:C
【点睛】本题考查图形面积的转化,抓住两个直角三角形的面积相等以及空白小三角形是公共部分解答。
10.B
【分析】先根据长方形的面积=长×宽,求出一个长方形的面积,再观察图形,第一层有一个长方形,第二层有两个长方形,第三层有三个长方形,则第几层就有几个长方形,以此类推,把十层长方形的数量相加,求出长方形的总数量,用长方形的总数量乘一个长方形的面积,即可解答。
【详解】2×1=2(cm2)
(1+2+3+4+5+6+7+8+9+10)×2
=(10+1)×(10÷2)×2
=11×5×2
=55×2
=110(cm2)
这个图形的面积是110cm2。
故答案为:B
【点睛】此题属于探索简单图形覆盖现象中的规律问题,考查学生总结规律的能力。
11.C
【分析】如图:假设中间的三角形为④,平行四边形的高和对边相等,分别是h、a,则②+③+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的底乘高除以2;三角形①+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的下底乘高除以2,即可得解。
【详解】假设中间的三角形为④,平行四边形的高为h,底边长为a,
则②+③+④的面积=a×h÷2,①+④的面积=a×h÷2,
所以②+③+④=①+④,
即①=②+③。
故答案为:C
【点睛】此题关键是利用中间量,通过三角形的面积公式,从而解决问题。
12.B
【分析】甲图的阴影部分是一个平行四边形,从图中可知,平行四边形的底小于正方形边长的一半,平行四边形的高等于正方形的边长;根据平行四边形的面积=底×高,正方形的面积=边长×边长,得出平行四边形的面积小于正方形面积的一半;
如下图,在乙图上画小方格,正方形共有32个小三角形,阴影部分有16个小三角形,所以乙图阴影部分的面积等于正方形面积的一半;
据此比较,得出结论。
【详解】甲图的阴影部分是一个平行四边形,平行四边形的面积小于正方形面积的一半;
乙图的阴影部分是4个小正方形,它们的面积之和等于正方形面积的一半。
因为两个正方形的面积相等,所以乙图阴影部分的面积>甲图阴影部分的面积。
综上所述,正方形中的阴影部分乙的面积更大。
故答案为:B
【点睛】本题考查组合图形面积的求法,把比较甲、乙两个图形阴影部分的面积转移到各图形阴影部分面积与正方形的面积相比较,进而得出结论。
13.B
【分析】阴影部分的面积可以由大的三角形面积减去小的三角形面积得到,结合三角形面积的计算公式,代入相应数值计算即可解答。
【详解】8×6÷2-(8÷2)×(6÷2)÷2
=48÷2-4×3÷2
=24-12÷2
=24-6
=18(cm2)
所以阴影部分的面积是18cm2。
故答案为:B
【点睛】解答本题的关键是把阴影部分的面积看作是大的三角形面积和小的三角形面积之差,再结合三角形面积的计算公式和数值大小计算即可。
14.B
【分析】设大、小正方形的边长分别为a和b,分别用a和b表示出每个图形中阴影部分的面积,再逐项判断即可。
【详解】设大、小正方形的边长分别为a和b,
①中阴影部分的面积为:ab;
②中阴影部分的面积为:ab;
③中阴影部分的面积为:a2;
④中阴影部分的面积为:b2;
A.图①中阴影部分的面积等于图②中阴影部分的面积,说法正确;
B.图②中阴影部分的面积不等于图③中阴影部分的面积,原说法错误;
C.图③中阴影部分的面积不等于图④中阴影部分的面积,说法正确。
故答案为:B
【点睛】分别用a和b表示出每个图形中阴影部分的面积,是解答此题的关键。
15.√
【分析】多边形里面三角形的内角和是180°,180°的2倍是360°;正四边形的每个角是90°,90°的4倍是360°;正六边形的每个角是120°,120°的3倍是360°;因此多边形中有三角形、正四边形、正六边形可以密铺,正五边形不能密铺;长方形的每个角是90°,所以长方形可以密铺,平行四边形同一边的角和是180°,180°的2倍是360°,所以平行四边形也可以密铺;据此解答。
【详解】长方形、三角形、平行四边形、正六边形都可以单独密铺。原题干说法正确。
故答案为:√
【点睛】本题主要考查了密铺的知识,注意判断图形对应的角能否组成360°。
16.√
【分析】不规则图形面积的估算方法:可以借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
【详解】不规则图形的面积可以转化为学过的图形来估算,说法正确。
故答案为:√
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
17.×
【分析】把不规则图形看成近似于规则的图形估算面积,有时候估算的面积比实际面积大,有时候估算的面积比实际面积小。
【详解】根据分析,估算的面积一般比实际面积大,说法错误。
故答案为:×
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
18.√
【详解】
由图可知,甲与乙分别加上中间的丙后是同底的平行四边形,
由于两个平行四边形是同底等高,面积相等,所以都减去公共部分丙后所得的甲和乙面积也是相等的;
即甲、乙两部分面积一样大,原题说法正确。
故答案为:√。
19.×
【分析】求组合图形的面积,有时是求几个简单图形的面积和,有时是求几个简单图形的面积之差。
【详解】如图:求阴影部分面积,就是求长方形与三角形的面积的差。
故答案为×。
【点睛】要考虑两种情况。
20.312m2
【分析】观察图形可知,该组合图形的面积等于平行四边形的面积加上三角形的面积,根据平行四边形的面积公式:S=ah,三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】24×8+24×10÷2
=192+120
=312(m2)
21.24平方厘米
【分析】观察图形可知,阴影部分是一个上底4厘米,下底8厘米,高4厘米的梯形,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出涂色部分的面积。
【详解】(4+8)×4÷2
=12×4÷2
=24(平方厘米)
图中涂色部分的面积是24平方厘米。
22.440棵
【分析】如下图,通过添加辅助线,将这块地分成一个长方形和一个三角形。长方形的长是15米,宽是5米,根据长方形的面积=长×宽,用15×5可求出长方形的面积;三角形的底是(15-5)米,高是(12-5)米,根据三角形的面积=底×高÷2,用(15-5)×(12-5)÷2可求出三角形的面积;再用长方形的面积加上三角形的面积求出这块地的面积;最后用这块地的面积除以每棵白菜的占地面积,求出能种白菜的棵数。
【详解】15×5=75(平方米)
(15-5)×(12-5)÷2
=10×7÷2
=70÷2
=35(平方米)
75+35=110(平方米)
110÷0.25=440(棵)
答:这块地能种440棵白菜。
【点睛】计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
23.3.792千克
【分析】将数据代入长方形面积公式:S=ab及三角形面积公式:S=ah÷2求出侧面墙的面积,再用侧面墙的面积×每平方米用石灰的质量即可。
【详解】4.8×3.2+4.8×1.5÷2
=15.36+7.2÷2
=15.36+3.6
=18.96(平方米)
18.96×0.2=3.792(千克)
答:一共要用3.792千克石灰。
【点睛】本题主要考查求组合图形面积的方法,运用长方形、三角形面积公式求出侧面墙的面积是解题的关键。
24.166.6平方米
【分析】观察图形可知,石子路是一个平行四边形,则草地部分的面积=长方形的面积-平行四边形的面积,根据长方形的面积=长×宽,平行四边形的面积=底×高,代入数据计算求解。
【详解】长方形的面积:17×11=187(平方米)
平行四边形的面积:1.2×17=20.4(平方米)
草地的面积:187-20.4=166.6(平方米)
答:草地部分的面积有166.6平方米。
【点睛】本题考查组合图形面积的求法,关键是分析出组合图形的面积是由哪些图形面积相加或相减得到,再根据图形面积公式解答。
25.1.1平方米
【分析】如图:
将图形分为3部分,一个长(1.5-0.5)米、宽0.5米的长方形,一个长0.8米、宽0.5米的长方形,一个底为1米,高为0.4米的三角形,根据长方形的面积=长×宽,三角形的面积=底×高÷2,代入数据分别求出每个部分的面积,然后相加即可。
【详解】(1.5-0.5)×0.5
=1×0.5
=0.5(平方米)
0.8×0.5=0.4(平方米)
1×0.4÷2=0.2(平方米)
0.5+0.4+0.2=1.1(平方米)
答:这个指示牌的面积是1.1平方米。
【点睛】本题主要考查了长方形面积公式、三角形的面积公式的灵活应用,要熟练掌握相关公式。
答案第1页,共2页
答案第1页,共2页
人教版 五年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.小美的父母计划购买一套公寓,小美想估计一下房屋的总面积(包括露台和墙,如户型图所示)。以下是小美测量的4种方式,你觉得这些方式都能估计出房屋的总面积吗?如果可以请在括号里打“√”,如果不可以请在括号里打“×”。
户型图 ( ) ( ) ( ) ( )
2.下图中每个小方格的面积表示1cm2,图1中涂色部分的面积是( )cm2,图2中图案的面积约是( )cm2。
图1 图2
3.如下图,平行四边形的面积是64cm2,则涂色部分的面积是( )cm2。
(第3题) (第4题)
4.如图所示,若阴影部分的面积是54cm2,则一个小正方形的面积是( )cm2。
5.陈燕从一个直角三角形纸板上剪下了一个正方形(如下图),剩下部分的面积是( )平方厘米。
6.小丽从一个上底为12.4厘米、下底为18.6厘米、高为4厘米的梯形卡纸中,剪掉一个最大的三角形,剩下卡纸的面积是( )平方厘米。
二、选择题
7.下图中这个精美的皮影人物的面积大约是( )平方厘米。(图中每个小方格的面积是4平方厘米)
A.24 B.96 C.60
8.有一个长方形,它的长减少5cm,面积就减少30cm2,剩下的部分正好是一个正方形。这个长方形的面积是( )cm2。
A.55 B.30 C.66
9.两个完全一样的直角三角形重叠成下图的形状,形成两个梯形,这两个梯形的面积相比。( )。
A.a大 B.b大 C.相等
10.把长2cm,宽1cm的长方形一层、二层、三层…有规律地摆下去(如图),摆到第十层时,这个图形的面积是( )cm2。
A.20 B.110 C.100
11.如图平行四边形中有①②③三个三角形,关于这三个三角形面积间的关系,下面的说法正确的是( )。
A.①>②+③ B.①<②+③ C.①=②+③
12.如图所示,是两个大小相同的正方形,正方形中的阴影部分哪一个面积更大?( )
A.甲大 B.乙大 C.一样大
13.图中A、B两点分别是长方形长和宽的中点,则阴影部分的面积是( )cm2。
A.32 B.18 C.16
14.比较下面阴影部分的面积,( )是错误的。
① ② ③ ④
A.图①中阴影部分的面积等于图②中阴影部分的面积
B.图②中阴影部分的面积等于图③中阴影部分的面积
C.图③中阴影部分的面积不等于图④中阴影部分的面积
三、判断题
15.长方形、三角形、平行四边形、正六边形都可以单独密铺。( )
16.不规则图形的面积可以转化为学过的图形来估算。( )
17.估算的面积一般比实际面积大。( )
18.如图,甲、乙两部分面积一样大。( )
19.求组合图形的面积,就是求几个简单图形的面积和. ( )
四、图形计算
20.求下图的面积。
21.下面是两个不同大小的正方形组合而成的图形,请你求出图中涂色部分的面积。(单位:厘米)
五、解答题
22.如下图,张叔叔准备在这块地里种白菜,如果每棵白菜占地0.25平方米,这块地能种多少棵白菜?
23.下图是一间房屋的侧面墙,如果用石灰粉刷这面墙,每平方米用石灰0.2千克,一共要用多少千克石灰?
24.公园有一块长方形草地,长方形的长是17米,宽是11米,中间铺了一条石子路,那么,草地部分的面积有多大?
25.郑州东站地处河南省省会郑州市市区东部,是全国唯一一个7个方向均是设计时速350千米的“米”字型高铁枢纽,同时也是一个涵盖高铁、城际、地铁、高速公路客运、城市公交、城市出租等多种交通方式的综合一体化交通枢纽。为方便旅客进出站,车站设置了很多方向指示牌。下图就是这些指示牌中的一种,根据图中的数据,算一算这个指示牌的面积有多大。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1. √ √ √ √
【分析】这个户型图是一个不规则图形,可以运用分割法或添补法把图形分成几个规则图形,分别量出需要的数据计算出它们的面积,再把各图形的面积相加即可求出房屋的总面积。
【详解】如下图所示,图1把图形分割成两个长方形,下面的长方形测量出了长和宽,上面的长方形长已知,宽可以计算出来,根据长方形的面积=长×宽,可以分别求出它们的面积,再把它们的面积相加即可;图2同样分成两个长方形,长方形的长和宽通过测量或计算都可以得到,则可以求出面积,继而求出房屋的总面积;图3添补成一个长方形,可以用整个长方形的面积减去右上角的小长方形的面积,即可求出房屋的总面积;图4左边的长方形测量了长和宽,右边的小长方形通过计算可以得到长,宽以测量出来,则可以求出各长方形的面积,继而求出房屋的总面积。
所以,这4种测量方式都能估计出房屋的总面积,括号里面都应打“√”。
【点睛】本题考查组合图形的面积。运用分割法或添补法把图形分成几个规则图形是解题的关键。
2. 6.5 4
【分析】不规则图形的面积估算方法:数格子,分别数出满格和不满格的数量,不满格的数量按半格计算,再加上满格的数量,就是不规则图形的格子数,最后乘每个小方格的面积即可。
【详解】(1)满格有4个,不满格有5个;
一共有:
4+5÷2
=4+2.5
=6.5(个)
面积:1×6.5=6.5(cm2)
图1中涂色部分的面积是6.5cm2。
(2)只有不满格的,有8个;
一共有:8÷2=4(个)
面积:1×4=4(cm2)
图2中图案的面积约是4cm2。
【点睛】掌握不规则图形面积的估算方法是解题的关键。
3.32
【分析】观察图形可知,涂色部分是两个三角形的和,两个三角形的底的和等于平行四边形的底,三角形的高等于平行四边形的高;根据三角形面积公式:面积=底×高÷2;平行四边形面积公式:面积=底×高;由此可知,涂色部分的面积等于平行四边形面积的一半;即平行四边形面积÷2=涂色部分的面积,据此求出涂色部分的面积。
【详解】64÷2=32(cm2)
即涂色部分的面积是32cm2。
【点睛】解答本题的关键明确阴影部分的底的和与平行四边形的底的关系,阴影部分的高与平行四边形的高之间的关系是解答本题的关键。
4.9
【分析】数一数涂色部分的面积一共是由6个小正方形组成的,所以用涂色部分的面积除以正方形的个数即可求出一个小正方形的面积。
【详解】54÷6=9(cm2)
即一个小正方形的面积是9cm2。
【点睛】此题的解题关键是通过转化的数学思想,把阴影部分的面积转化成正方形的面积。
5.24
【分析】通过旋转,可将阴影部分变化为如下图:
阴影部分相当于一个底为8厘米,高为6厘米的直角三角形,根据三角形的面积=底×高÷2,用8×6÷2即可求出阴影部分的面积。
【详解】8×6÷2=24(平方厘米)
剩下部分的面积是24平方厘米。
【点睛】解答本题的关键是学会转化阴影部分的面积,将其变成容易计算的图形。
6.24.8
【分析】要想在这个梯形卡纸中剪去一个最大的三角形,必须把梯形的下底作为三角形的底。把梯形的高作为三角形的高,则剩下的图形的面积就是以梯形的上底为底,梯形的高为高的三角形的面积,据此利用三角形的面积公式计算即可解答。
【详解】12.4×4÷2=24.8(平方厘米)
即剩下卡纸的面积是24.8平方厘米。
【点睛】此题考查组合图形的面积,解决此题关键是弄明白怎么剪才能使三角形的面积最大,进而得出剩下的是以上底为底边的三角形的面积。
7.C
【分析】用数小方格的方法估算不规则图形的面积,通常是先数整格数,再数不足格数,整格数按一个面积单位计算,不足格的按半个面积单位计算。
【详解】观察图形可知,不足格大概有26个。
26÷2=13
13×4=52(平方厘米)
52比较接近60,所以这个精美的皮影人物的面积大约是60平方厘米。
故答案为:C
【点睛】用数小方格的方法估算不规则图形的面积,通常是先数整格数,再数不足格数,整格数按一个面积单位计算,不足格的按半个面积单位计算。注意:数格是按一定的顺序数,既不要重复,也不要遗漏。
8.C
【分析】由题意得:长方形的长减去5cm等于长方形的宽。根据长方形面积=长×宽,算出长方形的宽,因为剩下的部分正好是一个正方形,那么剩下的正方形的边长为6,则可以算出长方形的长,再计算长方形的面积即可。
【详解】长方形的宽:305=6(cm)
长方形的长:65=11(cm)
长方形的面积:11 6=66(cm2)
故答案为:C
【点睛】本题考查了长方形以及正方形的知识点。掌握长方形和正方形的特征以及面积公式是关键。
9.C
【分析】从图中可知,一个直角三角形是由梯形a和空白小三角形组成,另一个直角三角形是由梯形b和空白小三角形组成,因为两个直角三角形完全一样,它们的面积相等,空白小三角形是公共部分,由此得出梯形a和b的面积关系。
【详解】梯形a的面积+空白小三角形的面积=梯形b的面积+空白小三角形的面积
所以梯形a的面积=梯形b的面积
故答案为:C
【点睛】本题考查图形面积的转化,抓住两个直角三角形的面积相等以及空白小三角形是公共部分解答。
10.B
【分析】先根据长方形的面积=长×宽,求出一个长方形的面积,再观察图形,第一层有一个长方形,第二层有两个长方形,第三层有三个长方形,则第几层就有几个长方形,以此类推,把十层长方形的数量相加,求出长方形的总数量,用长方形的总数量乘一个长方形的面积,即可解答。
【详解】2×1=2(cm2)
(1+2+3+4+5+6+7+8+9+10)×2
=(10+1)×(10÷2)×2
=11×5×2
=55×2
=110(cm2)
这个图形的面积是110cm2。
故答案为:B
【点睛】此题属于探索简单图形覆盖现象中的规律问题,考查学生总结规律的能力。
11.C
【分析】如图:假设中间的三角形为④,平行四边形的高和对边相等,分别是h、a,则②+③+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的底乘高除以2;三角形①+④组成一个大三角形,面积是平行四边形的一半,等于平行四边形的下底乘高除以2,即可得解。
【详解】假设中间的三角形为④,平行四边形的高为h,底边长为a,
则②+③+④的面积=a×h÷2,①+④的面积=a×h÷2,
所以②+③+④=①+④,
即①=②+③。
故答案为:C
【点睛】此题关键是利用中间量,通过三角形的面积公式,从而解决问题。
12.B
【分析】甲图的阴影部分是一个平行四边形,从图中可知,平行四边形的底小于正方形边长的一半,平行四边形的高等于正方形的边长;根据平行四边形的面积=底×高,正方形的面积=边长×边长,得出平行四边形的面积小于正方形面积的一半;
如下图,在乙图上画小方格,正方形共有32个小三角形,阴影部分有16个小三角形,所以乙图阴影部分的面积等于正方形面积的一半;
据此比较,得出结论。
【详解】甲图的阴影部分是一个平行四边形,平行四边形的面积小于正方形面积的一半;
乙图的阴影部分是4个小正方形,它们的面积之和等于正方形面积的一半。
因为两个正方形的面积相等,所以乙图阴影部分的面积>甲图阴影部分的面积。
综上所述,正方形中的阴影部分乙的面积更大。
故答案为:B
【点睛】本题考查组合图形面积的求法,把比较甲、乙两个图形阴影部分的面积转移到各图形阴影部分面积与正方形的面积相比较,进而得出结论。
13.B
【分析】阴影部分的面积可以由大的三角形面积减去小的三角形面积得到,结合三角形面积的计算公式,代入相应数值计算即可解答。
【详解】8×6÷2-(8÷2)×(6÷2)÷2
=48÷2-4×3÷2
=24-12÷2
=24-6
=18(cm2)
所以阴影部分的面积是18cm2。
故答案为:B
【点睛】解答本题的关键是把阴影部分的面积看作是大的三角形面积和小的三角形面积之差,再结合三角形面积的计算公式和数值大小计算即可。
14.B
【分析】设大、小正方形的边长分别为a和b,分别用a和b表示出每个图形中阴影部分的面积,再逐项判断即可。
【详解】设大、小正方形的边长分别为a和b,
①中阴影部分的面积为:ab;
②中阴影部分的面积为:ab;
③中阴影部分的面积为:a2;
④中阴影部分的面积为:b2;
A.图①中阴影部分的面积等于图②中阴影部分的面积,说法正确;
B.图②中阴影部分的面积不等于图③中阴影部分的面积,原说法错误;
C.图③中阴影部分的面积不等于图④中阴影部分的面积,说法正确。
故答案为:B
【点睛】分别用a和b表示出每个图形中阴影部分的面积,是解答此题的关键。
15.√
【分析】多边形里面三角形的内角和是180°,180°的2倍是360°;正四边形的每个角是90°,90°的4倍是360°;正六边形的每个角是120°,120°的3倍是360°;因此多边形中有三角形、正四边形、正六边形可以密铺,正五边形不能密铺;长方形的每个角是90°,所以长方形可以密铺,平行四边形同一边的角和是180°,180°的2倍是360°,所以平行四边形也可以密铺;据此解答。
【详解】长方形、三角形、平行四边形、正六边形都可以单独密铺。原题干说法正确。
故答案为:√
【点睛】本题主要考查了密铺的知识,注意判断图形对应的角能否组成360°。
16.√
【分析】不规则图形面积的估算方法:可以借助方格图数格子估算不规则图形的面积,也可以把不规则图形看成近似于规则的图形估算面积。
【详解】不规则图形的面积可以转化为学过的图形来估算,说法正确。
故答案为:√
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
17.×
【分析】把不规则图形看成近似于规则的图形估算面积,有时候估算的面积比实际面积大,有时候估算的面积比实际面积小。
【详解】根据分析,估算的面积一般比实际面积大,说法错误。
故答案为:×
【点睛】用数格子估计不规则图形面积的方法:分别数出整数格数合不完整格数;再定:根据整数格数和所有格数确定面积大小的范围;后估:把不完整格按半格计算加上整数格,估算出面积。
18.√
【详解】
由图可知,甲与乙分别加上中间的丙后是同底的平行四边形,
由于两个平行四边形是同底等高,面积相等,所以都减去公共部分丙后所得的甲和乙面积也是相等的;
即甲、乙两部分面积一样大,原题说法正确。
故答案为:√。
19.×
【分析】求组合图形的面积,有时是求几个简单图形的面积和,有时是求几个简单图形的面积之差。
【详解】如图:求阴影部分面积,就是求长方形与三角形的面积的差。
故答案为×。
【点睛】要考虑两种情况。
20.312m2
【分析】观察图形可知,该组合图形的面积等于平行四边形的面积加上三角形的面积,根据平行四边形的面积公式:S=ah,三角形的面积公式:S=ah÷2,据此进行计算即可。
【详解】24×8+24×10÷2
=192+120
=312(m2)
21.24平方厘米
【分析】观察图形可知,阴影部分是一个上底4厘米,下底8厘米,高4厘米的梯形,根据梯形的面积=(上底+下底)×高÷2,代入数据计算,即可求出涂色部分的面积。
【详解】(4+8)×4÷2
=12×4÷2
=24(平方厘米)
图中涂色部分的面积是24平方厘米。
22.440棵
【分析】如下图,通过添加辅助线,将这块地分成一个长方形和一个三角形。长方形的长是15米,宽是5米,根据长方形的面积=长×宽,用15×5可求出长方形的面积;三角形的底是(15-5)米,高是(12-5)米,根据三角形的面积=底×高÷2,用(15-5)×(12-5)÷2可求出三角形的面积;再用长方形的面积加上三角形的面积求出这块地的面积;最后用这块地的面积除以每棵白菜的占地面积,求出能种白菜的棵数。
【详解】15×5=75(平方米)
(15-5)×(12-5)÷2
=10×7÷2
=70÷2
=35(平方米)
75+35=110(平方米)
110÷0.25=440(棵)
答:这块地能种440棵白菜。
【点睛】计算组合图形的面积,要根据已知条件对图形进行分割,转化成已学过的简单图形,先分别计算出它们的面积,再求和或差。
23.3.792千克
【分析】将数据代入长方形面积公式:S=ab及三角形面积公式:S=ah÷2求出侧面墙的面积,再用侧面墙的面积×每平方米用石灰的质量即可。
【详解】4.8×3.2+4.8×1.5÷2
=15.36+7.2÷2
=15.36+3.6
=18.96(平方米)
18.96×0.2=3.792(千克)
答:一共要用3.792千克石灰。
【点睛】本题主要考查求组合图形面积的方法,运用长方形、三角形面积公式求出侧面墙的面积是解题的关键。
24.166.6平方米
【分析】观察图形可知,石子路是一个平行四边形,则草地部分的面积=长方形的面积-平行四边形的面积,根据长方形的面积=长×宽,平行四边形的面积=底×高,代入数据计算求解。
【详解】长方形的面积:17×11=187(平方米)
平行四边形的面积:1.2×17=20.4(平方米)
草地的面积:187-20.4=166.6(平方米)
答:草地部分的面积有166.6平方米。
【点睛】本题考查组合图形面积的求法,关键是分析出组合图形的面积是由哪些图形面积相加或相减得到,再根据图形面积公式解答。
25.1.1平方米
【分析】如图:
将图形分为3部分,一个长(1.5-0.5)米、宽0.5米的长方形,一个长0.8米、宽0.5米的长方形,一个底为1米,高为0.4米的三角形,根据长方形的面积=长×宽,三角形的面积=底×高÷2,代入数据分别求出每个部分的面积,然后相加即可。
【详解】(1.5-0.5)×0.5
=1×0.5
=0.5(平方米)
0.8×0.5=0.4(平方米)
1×0.4÷2=0.2(平方米)
0.5+0.4+0.2=1.1(平方米)
答:这个指示牌的面积是1.1平方米。
【点睛】本题主要考查了长方形面积公式、三角形的面积公式的灵活应用,要熟练掌握相关公式。
答案第1页,共2页
答案第1页,共2页
