北师大版七下5.1 认识三角形(AB卷) (含答案)-
文档属性
| 名称 | 北师大版七下5.1 认识三角形(AB卷) (含答案)- |  | |
| 格式 | rar | ||
| 文件大小 | 138.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-05-25 21:14:00 | ||
图片预览



文档简介
第五章 认识三角形(A)
一、选择题
1.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为 ( )
A.10 B.12 C.14 D.16
2.在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( )
A.a>2 B.2<a<14 C.7<a<14 D.a<14
3.一个三角形的三个内角中,锐角的个数最少为 ( )
A.0 B.1 C.2 D.3
4.下面说法错误的是 ( )
A.三角形的三条角平分线交于一点 B.三角形的三条中线交于一点
C.三角形的三条高交于一点 D.三角形的三条高所在的直线交于一点
5.能将一个三角形分成面积相等的两个三角形的一条线段是 ( )
A.中线 B.角平分线 C.高线 D.三角形的角平分线
6.如图5—12,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是 ( )
A.∠1 B.∠2 C.∠B D.∠1、∠2和∠B
7.点P是△ABC内任意一点,则∠APC与∠B的大小关系是 ( ) A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
8.已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么 ( )
A.M>0 B.M=0 C.M<0 D.不能确定
9.周长为P的三角形中,最长边m的取值范围是 ( )
A. B. C. D.
10.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
1.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以________个三角形.
2.在△ABC中,AB=6,AC=10,那么BC边的取值范围是________,周长的取值范围是___________.
3.一个三角形的三个内角的度数的比是2:2:1,这个三角形是_________三角形.
4.一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
5.在△ABC中,三边长分别为正整数a、b、c,且c≥b≥a>0,如果b=4,则这样的三角形共有_________个.
6.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________.
7.在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________.
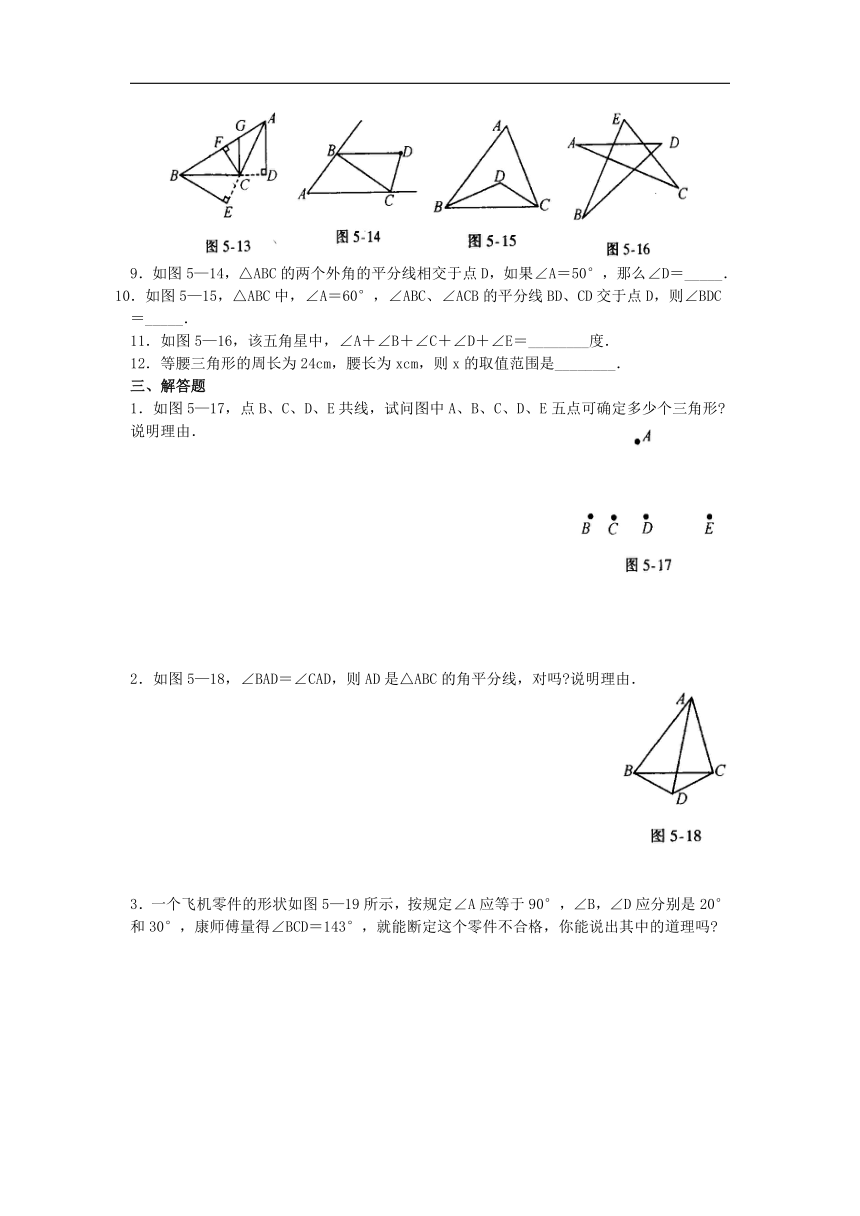
8.如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是 △ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.
9.如图5—14,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.
10.如图5—15,△ABC中,∠A=60°,∠ABC、∠ACB的平分线BD、CD交于点D,则∠BDC=_____.
11.如图5—16,该五角星中,∠A+∠B+∠C+∠D+∠E=________度.
12.等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是________.
三、解答题
1.如图5—17,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形 说明理由.
2.如图5—18,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗 说明理由.
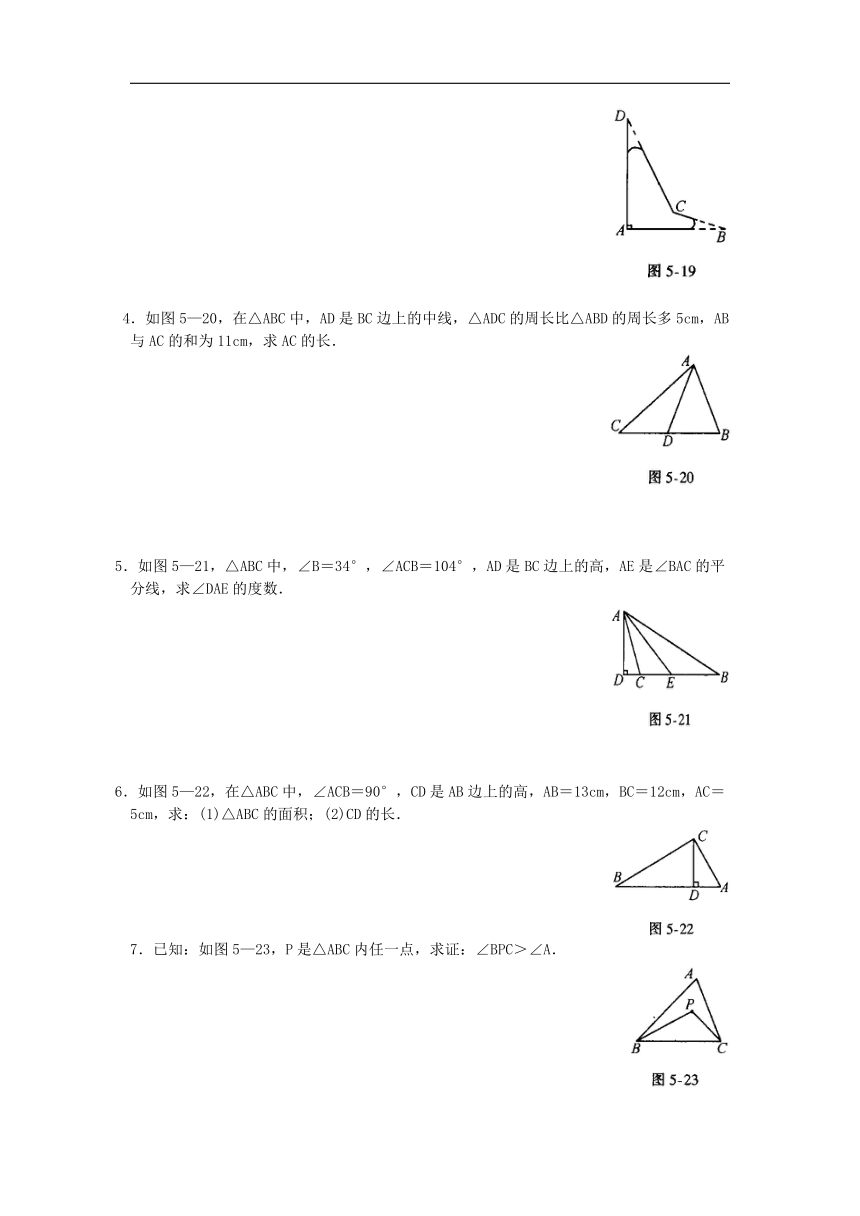
3.一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗
4.如图5—20,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.
5.如图5—21,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
6.如图5—22,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
7.已知:如图5—23,P是△ABC内任一点,求证:∠BPC>∠A.
8.△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.
9.已知:如图5—24,P是△ABC内任一点,求证:AB+AC>BP+PC.
10.如图5—25,豫东有四个村庄A、B、C、D.现在要建造一个水塔P.请回答水塔P应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.
答案:
一、1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C
二、1.3; 2.; 3.锐角(等腰锐角); 4.;5.10; 6.和; 7.; 8.;9.; 10.; 11.; 12..
三、
1.可以确定6个三角形.理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,所以图中可以确定6个三角形.
2.错误.因为AD虽然是线段,但不符合三角形角平分线定义,这里射线AD是的平分线.
3.假设此零件合格,连接BD,则;可知.这与上面的结果不一致,从而知这个零件不合格.
4.∵ AD是BC边上的中线,
∴ D为BC的中点,.
∵ 的周长-的周长=5cm.
∴ .
又∵ ,
∴ .
5.由三角形内角和定理,得
.
∴ .
又∵ AE平分∠BAC.
∴ .
∴ .
又∵ ,
∴ .
6.(1)∵ 在△ABC中,,,,
(2)∵ CD是AB边上的高,
∴ .
即.
∴ .
7.如图,延长BP交AC于D,
∵ ,
∴ .
8.∵ ,
∴ ,
∴ .
又∵ ,
∴ .
∴ ,
∵ ,
∴ .
又∵ 为整数,
∴ ∠C的度数为7的倍数.
∴ ,∴ .
9.如图,延长BP交AC于点D.在△BAD中,,
即:.
在△PDC中,.
①+②得
,
即.
10.如图,水塔P应建在线段AC和线段BD的交点处.这样的设计将最节省材料.
理由:我们不妨任意取一点,连结、、、、、、、,
∵ 在中,, ①
在中,, ②
①+②得.
∵ 点是任意的,代表一般性,
∴ 线段AC和BD的交点处P到4个村的距离之和最小.
第五章 认识三角形(B)
1.一定在△ABC内部的线段是( )
A.锐角三角形的三条高、三条角平分线、三条中线
B.钝角三角形的三条高、三条中线、一条角平分线
C.任意三角形的一条中线、二条角平分线、三条高
D.直角三角形的三条高、三条角平分线、三条中线
2.下列说法中,正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
3.如图,在△ABC中,D、E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有( ) A.4对 B.5对 C.6对 D.7对
(注意考虑完全,不要漏掉某些情况)
4.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
5.下列各题中给出的三条线段不能组成三角形的是( )
A.a+1,a+2,a+3(a>0) B.三条线段的比为4∶6∶10
C.3cm,8cm,10cm D.3a,5a,2a+1(a>0)
6.若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是( )
A.18 B.15 C.18或15 D.无法确定
7.两根木棒分别为5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,那么第三根木棒的取值情况有( )种
A.3 B.4 C.5 D.6
8.△ABC的三边a、b、c都是正整数,且满足a≤b≤c,如果b=4,那么这样的三角形共有( )个 A.4 B.6 C.8 D.10
9.各边长均为整数的不等边三角形的周长小于13,这样的三角形有( )
A.1个 B.2个 C.3个 D.4个
10.三角形所有外角的和是( )
A.180° B.360° C.720° D.540°
11.锐角三角形中,最大角α的取值范围是( )
A.0°<α<90°; B.60°<α<180°; C.60°<α<90°; D.60°≤α<90°
12.如果三角形的一个外角不大于和它相邻的内角,那么这个三角形为( )
A.锐角或直角三角形; B.钝角或锐角三角形;C.直角三角形; D.钝角或直角三角形
13.已知△ABC中,∠ABC与∠ACB的平分线交于点O,则∠BOC一定( )
A.小于直角; B.等于直角; C.大于直角; D.大于或等于直角
14.如图:(1)AD⊥BC,垂足为D,则AD是________的高,
∠________=∠________=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫________,
∠________=∠________=∠________,AH叫________;
(3)若AF=FC,则△ABC的中线是________;
(4)若BG=GH=HF,则AG是________的中线,AH是________的中线.
15.如图,∠ABC=∠ADC=∠FEC=90°.
(1)在△ABC中,BC边上的高是________;
(2)在△AEC中,AE边上的高是________;
(3)在△FEC中,EC边上的高是________;
(4)若AB=CD=3,AE=5,则△AEC的面积为________.
16.在等腰△ABC中,如果两边长分别为6cm、10cm,则这个等腰三角形的周长为________.
17.五段线段长分别为1cm、2cm、3cm、4cm、5cm,以其中三条线段为边长共可以组成________个三角形.
18.已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________.
19.一个等腰三角形的周长为5cm,如果它的三边长都是整数,那么它的腰长为________cm.
20.在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则∠A=______;∠B=______;∠C=______.
21.如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.
(1)若∠ABC=70°,∠ACB=50°,则∠BIC=________;
(2)若∠ABC+∠ACB=120°,则∠BIC=________;
(3)若∠A=60°,则∠BIC=________;
(4)若∠A=100°,则∠BIC=________;
(5)若∠A=n°,则∠BIC=________.
22.如图,在△ABC中,∠BAC是钝角.
画出:(1)∠ABC的平分线;
(2)边AC上的中线;
(3)边AC上的高.
23.△ABC的周长为16cm,AB=AC,BC边上的中线AD把△ABC分成周长相等的两个三角形.若BD=3cm,求AB的长.
24.如图,AB∥CD,BC⊥AB,若AB=4cm,,求△ABD中AB边上的高.
25.学校有一块菜地,如下图.现计划从点D表示的位置(BD∶DC=2∶1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.有人说:如果D是BC的中点的话,由此点D笔直地挖至点A就可以了.现在D不是BC的中点,问题就无法解决了.但有人认为如果认真研究的话一定能办到.你认为上面两种意见哪一种正确,为什么
26.在直角△ABC中,∠BAC=90°,如下图所示.作BC边上的高,图中出现三个直角三角形(3=2×1+1);又作△ABD中AB边上的高,这时图中便出现五个不同的直角三角形(5=2×2+1);按照同样的方法作、、……、.当作出时,图中共有多少个不同的直角三角形
27.一块三角形优良品种试验田,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块.请你制订出两种以上的划分方案.
28.一个三角形的周长为36cm,三边之比为a∶b∶c=2∶3∶4,求a、b、c.
11.已知△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,求△ABC各边的长.
29.已知三角形三边的长分别为:5、10、a-2,求a的取值范围.
30.已知等腰三角形中,AB=AC,一腰上的中线BD把这个三角形的周长分成15cm和6cm两部分,求这个等腰三角形的底边的长.
31.如图,已知△ABC中,AB=AC,D在AC的延长线上.
求证:BD-BC<AD-AB.
32.如图,△ABC中,D是AB上一点.
求证:(1)AB+BC+CA>2CD;(2)AB+2CD>AC+BC.
33.如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,
(1)完成下面的证明:
∵ MG平分∠BMN( ),
∴ ∠GMN=∠BMN( ),
同理∠GNM=∠DNM.
∵ AB∥CD( ),
∴ ∠BMN+∠DNM=________( ).
∴ ∠GMN+∠GNM=________.
∵ ∠GMN+∠GNM+∠G=________( ),
∴ ∠G= ________.
∴ MG与NG的位置关系是________.
(2)把上面的题设和结论,用文字语言概括为一个命题:
_______________________________________________________________.
34.已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数.
35.已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,
求∠BOC的度数.
36.已知,如图△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线.求∠DAE的度数.
37.已知,如图CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.
38.画出图形,并完成证明:
已知:AD是△ABC的外角∠EAC的平分线,且AD∥BC.
求证:∠B=∠C.
参考答案:
1.A; 2.D; 3.A; 4.C;5.B; 6.C; 7.B; 8.D;
9.C(提示:边长分别为3、4、5;2、4、5;2、3、4.)10.C; 11.D; 12.D; 13.C;
14.(1)BC边上,ADB,ADC;
(2)∠BAC的角平分线,BAE,CAE,BAC,∠BAF的角平分线;
(3)BF;
(4)△ABH,△AGF;
15.(1)AB; (2)CD; (3)EF; (4)7.5; 16.22cm或26cm; 17.3; 18.11; 19.2;5.90°,36°,54°;
20.(1)120°; (2)120°; (3)120°; (4)140°; (5);
21.略;
22.解法1:AB+BD+DA=DA+AC+CD,∴ BD=CD,
∵ BD=3cm,∴ CD=3cm,BC=6cm,∵ AB=AC,∴ AB=5cm.
解法2:△ABD与△ACD的周长相等,而AB=AC,∴ BD=CD,
∴ BC=2BD=6cm,∴ AB=(16-6)÷2=5cm.
23.,∴ AB·BC=12,AB=4,∴ BC=6,
∵ AB∥CD,∴ △ABD中AB边上的高=BC=6cm.
24.后一种意见正确.
25.不作垂线,一个直角三角形,即:1=2×0+1,
作一条垂线,三个直角三角形,即:3=2×1+1,同理,5=2×2+1,找出相应的规律,当作出时,图中共有2×k+1,即2k+1个直角三角形.
26.第一种方案:在BC上取E、D、F,使BE=ED=DF=FC,连结AE、AD、AF,则△ABE、△AED、△ADF、△AFC面积相等;
第二种方案:取AB、BC、CA的中点D、E、F,连结DE、EF、FD,则△ADF、△BDE、△CEF、△DEF面积相等.
27.设三边长a=2k,b=3k,c=4k,
∵ 三角形周长为36,∴ 2k+3k+4k=36,k=4,
∴ a=8cm,b=12cm,c=16cm.
28.设三角形中最大边为a,最小边为c,
由已知,a-c=14,b+c=25,a+b+c=48,
∴ a=23cm,b=16cm,c=9cm.
29.10-5<a-2<10+5,∴ 7<a<17.
30.设AB=AC=2x,则AD=CD=x,
(1)当AB+AD=15,BC+CD=6时,2x+x=15,∴ x=5,2x=10,
∴ BC=6-5=1cm;
(2)当AB+AD=6,BC+CD=15时,2x+x=6,∴ x=2,2x=4,
∴ BC=13cm;
经检验,第二种情况不符合三角形的条件,故舍去.
31.AD-AB=AC+CD-AB=CD,∵ BD-BC<CD,
∴ BD-BC<AD-AB.
32.(1)AC+AD>CD,BC+BD>CD,
两式相加:AB+BC+CA>2CD.
(2)AD+CD>AC,BD+CD>BC,
两式相加:AB+2CD>AC+BC.
33.(1)已知,角平分线定义,已知,180°,两直线平行同旁内角互补,90°,180°,三角形内角和定理,90°,互相垂直.
(2)两平行直线被第三条直线所截,它们的同旁内角的角平分线互相垂直.
34.94°; 35.120°; 36.10°;
37.∠EBC<∠DCE,而∠DCE=∠ACE,∴ ∠EBC<∠ACE.
38.略.
一、选择题
1.一个三角形的两边长为2和6,第三边为偶数.则这个三角形的周长为 ( )
A.10 B.12 C.14 D.16
2.在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( )
A.a>2 B.2<a<14 C.7<a<14 D.a<14
3.一个三角形的三个内角中,锐角的个数最少为 ( )
A.0 B.1 C.2 D.3
4.下面说法错误的是 ( )
A.三角形的三条角平分线交于一点 B.三角形的三条中线交于一点
C.三角形的三条高交于一点 D.三角形的三条高所在的直线交于一点
5.能将一个三角形分成面积相等的两个三角形的一条线段是 ( )
A.中线 B.角平分线 C.高线 D.三角形的角平分线
6.如图5—12,已知∠ACB=90°,CD⊥AB,垂足是D,则图中与∠A相等的角是 ( )
A.∠1 B.∠2 C.∠B D.∠1、∠2和∠B
7.点P是△ABC内任意一点,则∠APC与∠B的大小关系是 ( ) A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定
8.已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么 ( )
A.M>0 B.M=0 C.M<0 D.不能确定
9.周长为P的三角形中,最长边m的取值范围是 ( )
A. B. C. D.
10.各边长均为整数且三边各不相等的三角形的周长小于13,这样的三角形个数共有( )
A.5个 B.4个 C.3个 D.2个
二、填空题
1.五条线段的长分别为1,2,3,4,5,以其中任意三条线段为边长可以________个三角形.
2.在△ABC中,AB=6,AC=10,那么BC边的取值范围是________,周长的取值范围是___________.
3.一个三角形的三个内角的度数的比是2:2:1,这个三角形是_________三角形.
4.一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
5.在△ABC中,三边长分别为正整数a、b、c,且c≥b≥a>0,如果b=4,则这样的三角形共有_________个.
6.直角三角形中,两个锐角的差为40°,则这两个锐角的度数分别为_________.
7.在△ABC中,∠A-∠B=30°、∠C=4∠B,则∠C=________.
8.如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是 △ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.
9.如图5—14,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.
10.如图5—15,△ABC中,∠A=60°,∠ABC、∠ACB的平分线BD、CD交于点D,则∠BDC=_____.
11.如图5—16,该五角星中,∠A+∠B+∠C+∠D+∠E=________度.
12.等腰三角形的周长为24cm,腰长为xcm,则x的取值范围是________.
三、解答题
1.如图5—17,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形 说明理由.
2.如图5—18,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗 说明理由.
3.一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗
4.如图5—20,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.
5.如图5—21,△ABC中,∠B=34°,∠ACB=104°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
6.如图5—22,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
7.已知:如图5—23,P是△ABC内任一点,求证:∠BPC>∠A.
8.△ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.
9.已知:如图5—24,P是△ABC内任一点,求证:AB+AC>BP+PC.
10.如图5—25,豫东有四个村庄A、B、C、D.现在要建造一个水塔P.请回答水塔P应建在何位置,才能使它到4村的距离之和最小,说明最节约材料的办法和理由.
答案:
一、1.C 2.B 3.C 4.C 5.A 6.B 7.A 8.C 9.A 10.C
二、1.3; 2.; 3.锐角(等腰锐角); 4.;5.10; 6.和; 7.; 8.;9.; 10.; 11.; 12..
三、
1.可以确定6个三角形.理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,所以图中可以确定6个三角形.
2.错误.因为AD虽然是线段,但不符合三角形角平分线定义,这里射线AD是的平分线.
3.假设此零件合格,连接BD,则;可知.这与上面的结果不一致,从而知这个零件不合格.
4.∵ AD是BC边上的中线,
∴ D为BC的中点,.
∵ 的周长-的周长=5cm.
∴ .
又∵ ,
∴ .
5.由三角形内角和定理,得
.
∴ .
又∵ AE平分∠BAC.
∴ .
∴ .
又∵ ,
∴ .
6.(1)∵ 在△ABC中,,,,
(2)∵ CD是AB边上的高,
∴ .
即.
∴ .
7.如图,延长BP交AC于D,
∵ ,
∴ .
8.∵ ,
∴ ,
∴ .
又∵ ,
∴ .
∴ ,
∵ ,
∴ .
又∵ 为整数,
∴ ∠C的度数为7的倍数.
∴ ,∴ .
9.如图,延长BP交AC于点D.在△BAD中,,
即:.
在△PDC中,.
①+②得
,
即.
10.如图,水塔P应建在线段AC和线段BD的交点处.这样的设计将最节省材料.
理由:我们不妨任意取一点,连结、、、、、、、,
∵ 在中,, ①
在中,, ②
①+②得.
∵ 点是任意的,代表一般性,
∴ 线段AC和BD的交点处P到4个村的距离之和最小.
第五章 认识三角形(B)
1.一定在△ABC内部的线段是( )
A.锐角三角形的三条高、三条角平分线、三条中线
B.钝角三角形的三条高、三条中线、一条角平分线
C.任意三角形的一条中线、二条角平分线、三条高
D.直角三角形的三条高、三条角平分线、三条中线
2.下列说法中,正确的是( )
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形
B.一个等腰三角形一定是锐角三角形,或直角三角形
C.一个直角三角形一定不是等腰三角形,也不是等边三角形
D.一个等边三角形一定不是钝角三角形,也不是直角三角形
3.如图,在△ABC中,D、E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有( ) A.4对 B.5对 C.6对 D.7对
(注意考虑完全,不要漏掉某些情况)
4.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
5.下列各题中给出的三条线段不能组成三角形的是( )
A.a+1,a+2,a+3(a>0) B.三条线段的比为4∶6∶10
C.3cm,8cm,10cm D.3a,5a,2a+1(a>0)
6.若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是( )
A.18 B.15 C.18或15 D.无法确定
7.两根木棒分别为5cm和7cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,那么第三根木棒的取值情况有( )种
A.3 B.4 C.5 D.6
8.△ABC的三边a、b、c都是正整数,且满足a≤b≤c,如果b=4,那么这样的三角形共有( )个 A.4 B.6 C.8 D.10
9.各边长均为整数的不等边三角形的周长小于13,这样的三角形有( )
A.1个 B.2个 C.3个 D.4个
10.三角形所有外角的和是( )
A.180° B.360° C.720° D.540°
11.锐角三角形中,最大角α的取值范围是( )
A.0°<α<90°; B.60°<α<180°; C.60°<α<90°; D.60°≤α<90°
12.如果三角形的一个外角不大于和它相邻的内角,那么这个三角形为( )
A.锐角或直角三角形; B.钝角或锐角三角形;C.直角三角形; D.钝角或直角三角形
13.已知△ABC中,∠ABC与∠ACB的平分线交于点O,则∠BOC一定( )
A.小于直角; B.等于直角; C.大于直角; D.大于或等于直角
14.如图:(1)AD⊥BC,垂足为D,则AD是________的高,
∠________=∠________=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫________,
∠________=∠________=∠________,AH叫________;
(3)若AF=FC,则△ABC的中线是________;
(4)若BG=GH=HF,则AG是________的中线,AH是________的中线.
15.如图,∠ABC=∠ADC=∠FEC=90°.
(1)在△ABC中,BC边上的高是________;
(2)在△AEC中,AE边上的高是________;
(3)在△FEC中,EC边上的高是________;
(4)若AB=CD=3,AE=5,则△AEC的面积为________.
16.在等腰△ABC中,如果两边长分别为6cm、10cm,则这个等腰三角形的周长为________.
17.五段线段长分别为1cm、2cm、3cm、4cm、5cm,以其中三条线段为边长共可以组成________个三角形.
18.已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________.
19.一个等腰三角形的周长为5cm,如果它的三边长都是整数,那么它的腰长为________cm.
20.在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则∠A=______;∠B=______;∠C=______.
21.如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.
(1)若∠ABC=70°,∠ACB=50°,则∠BIC=________;
(2)若∠ABC+∠ACB=120°,则∠BIC=________;
(3)若∠A=60°,则∠BIC=________;
(4)若∠A=100°,则∠BIC=________;
(5)若∠A=n°,则∠BIC=________.
22.如图,在△ABC中,∠BAC是钝角.
画出:(1)∠ABC的平分线;
(2)边AC上的中线;
(3)边AC上的高.
23.△ABC的周长为16cm,AB=AC,BC边上的中线AD把△ABC分成周长相等的两个三角形.若BD=3cm,求AB的长.
24.如图,AB∥CD,BC⊥AB,若AB=4cm,,求△ABD中AB边上的高.
25.学校有一块菜地,如下图.现计划从点D表示的位置(BD∶DC=2∶1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.有人说:如果D是BC的中点的话,由此点D笔直地挖至点A就可以了.现在D不是BC的中点,问题就无法解决了.但有人认为如果认真研究的话一定能办到.你认为上面两种意见哪一种正确,为什么
26.在直角△ABC中,∠BAC=90°,如下图所示.作BC边上的高,图中出现三个直角三角形(3=2×1+1);又作△ABD中AB边上的高,这时图中便出现五个不同的直角三角形(5=2×2+1);按照同样的方法作、、……、.当作出时,图中共有多少个不同的直角三角形
27.一块三角形优良品种试验田,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块.请你制订出两种以上的划分方案.
28.一个三角形的周长为36cm,三边之比为a∶b∶c=2∶3∶4,求a、b、c.
11.已知△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,求△ABC各边的长.
29.已知三角形三边的长分别为:5、10、a-2,求a的取值范围.
30.已知等腰三角形中,AB=AC,一腰上的中线BD把这个三角形的周长分成15cm和6cm两部分,求这个等腰三角形的底边的长.
31.如图,已知△ABC中,AB=AC,D在AC的延长线上.
求证:BD-BC<AD-AB.
32.如图,△ABC中,D是AB上一点.
求证:(1)AB+BC+CA>2CD;(2)AB+2CD>AC+BC.
33.如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,
(1)完成下面的证明:
∵ MG平分∠BMN( ),
∴ ∠GMN=∠BMN( ),
同理∠GNM=∠DNM.
∵ AB∥CD( ),
∴ ∠BMN+∠DNM=________( ).
∴ ∠GMN+∠GNM=________.
∵ ∠GMN+∠GNM+∠G=________( ),
∴ ∠G= ________.
∴ MG与NG的位置关系是________.
(2)把上面的题设和结论,用文字语言概括为一个命题:
_______________________________________________________________.
34.已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数.
35.已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC=60°,
求∠BOC的度数.
36.已知,如图△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线.求∠DAE的度数.
37.已知,如图CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.
38.画出图形,并完成证明:
已知:AD是△ABC的外角∠EAC的平分线,且AD∥BC.
求证:∠B=∠C.
参考答案:
1.A; 2.D; 3.A; 4.C;5.B; 6.C; 7.B; 8.D;
9.C(提示:边长分别为3、4、5;2、4、5;2、3、4.)10.C; 11.D; 12.D; 13.C;
14.(1)BC边上,ADB,ADC;
(2)∠BAC的角平分线,BAE,CAE,BAC,∠BAF的角平分线;
(3)BF;
(4)△ABH,△AGF;
15.(1)AB; (2)CD; (3)EF; (4)7.5; 16.22cm或26cm; 17.3; 18.11; 19.2;5.90°,36°,54°;
20.(1)120°; (2)120°; (3)120°; (4)140°; (5);
21.略;
22.解法1:AB+BD+DA=DA+AC+CD,∴ BD=CD,
∵ BD=3cm,∴ CD=3cm,BC=6cm,∵ AB=AC,∴ AB=5cm.
解法2:△ABD与△ACD的周长相等,而AB=AC,∴ BD=CD,
∴ BC=2BD=6cm,∴ AB=(16-6)÷2=5cm.
23.,∴ AB·BC=12,AB=4,∴ BC=6,
∵ AB∥CD,∴ △ABD中AB边上的高=BC=6cm.
24.后一种意见正确.
25.不作垂线,一个直角三角形,即:1=2×0+1,
作一条垂线,三个直角三角形,即:3=2×1+1,同理,5=2×2+1,找出相应的规律,当作出时,图中共有2×k+1,即2k+1个直角三角形.
26.第一种方案:在BC上取E、D、F,使BE=ED=DF=FC,连结AE、AD、AF,则△ABE、△AED、△ADF、△AFC面积相等;
第二种方案:取AB、BC、CA的中点D、E、F,连结DE、EF、FD,则△ADF、△BDE、△CEF、△DEF面积相等.
27.设三边长a=2k,b=3k,c=4k,
∵ 三角形周长为36,∴ 2k+3k+4k=36,k=4,
∴ a=8cm,b=12cm,c=16cm.
28.设三角形中最大边为a,最小边为c,
由已知,a-c=14,b+c=25,a+b+c=48,
∴ a=23cm,b=16cm,c=9cm.
29.10-5<a-2<10+5,∴ 7<a<17.
30.设AB=AC=2x,则AD=CD=x,
(1)当AB+AD=15,BC+CD=6时,2x+x=15,∴ x=5,2x=10,
∴ BC=6-5=1cm;
(2)当AB+AD=6,BC+CD=15时,2x+x=6,∴ x=2,2x=4,
∴ BC=13cm;
经检验,第二种情况不符合三角形的条件,故舍去.
31.AD-AB=AC+CD-AB=CD,∵ BD-BC<CD,
∴ BD-BC<AD-AB.
32.(1)AC+AD>CD,BC+BD>CD,
两式相加:AB+BC+CA>2CD.
(2)AD+CD>AC,BD+CD>BC,
两式相加:AB+2CD>AC+BC.
33.(1)已知,角平分线定义,已知,180°,两直线平行同旁内角互补,90°,180°,三角形内角和定理,90°,互相垂直.
(2)两平行直线被第三条直线所截,它们的同旁内角的角平分线互相垂直.
34.94°; 35.120°; 36.10°;
37.∠EBC<∠DCE,而∠DCE=∠ACE,∴ ∠EBC<∠ACE.
38.略.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
