第5单元圆应用题特训卷(拔高卷)数学六年级上册人教版(含答案)
文档属性
| 名称 | 第5单元圆应用题特训卷(拔高卷)数学六年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-16 12:01:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第5单元圆应用题特训卷(拔高卷)数学六年级上册人教版
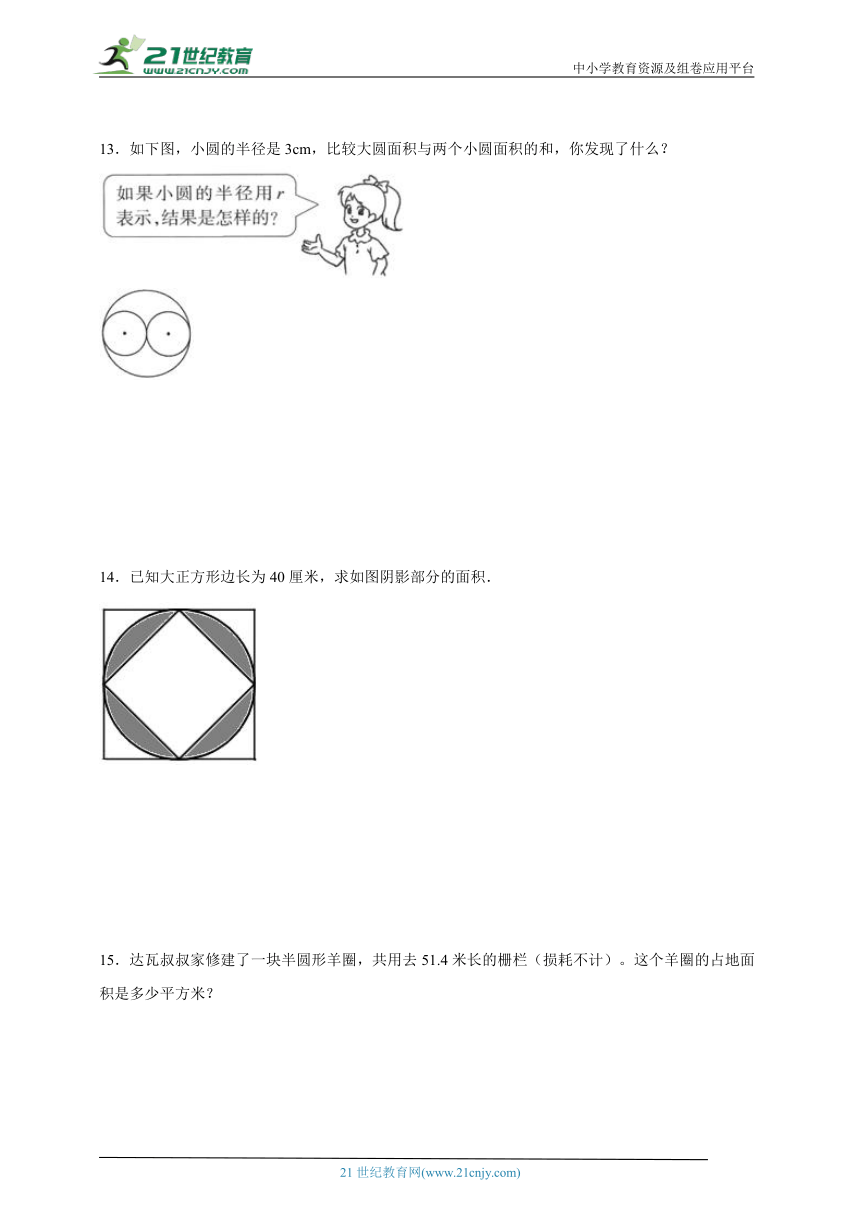
1.前轮在720米的距离里比后轮多转40周,如果后轮的周长是2米,求前轮的周长.
2.如图,一个椭圆形运动场,两端是由两个半圆组成的,奇思每天早晨都绕运动场跑6圈,奇思每天跑多少米?
3.大本钟——伦敦市的标志性建筑物,钟盘上时针的长度是2.75m。
(1)大本钟的时针经过8小时,时针的尖端走过的路程是多少米?(得数保留两位小数)
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了多少小时?
4.一台压路机的滚筒长1.5米,直径是0.8米,这台压路机滚动10周压过的路面是多少平方米?
5.牧民们打算在草原附近修建一共圆形的牛栏,半径为50米.
(1)如果每隔2米安装一根木桩,一圈一共要安装多少根木桩?
(2)如果用粗铁丝把这个牛栏围成5圈,(接头处忽略不计)至少需要铁丝多少米?
6.神舟十三号飞船在太空中绕地球飞行,飞行时离地面高度约400千米,每秒钟约飞行7.9千米,求飞船绕地球飞行一周大约需要多少小时。(地球半径约为6400千米,结果保留两位小数)
7.如图所示:圆的周长是25.12厘米,°,梯形OABC的面积是多少平方厘米?
A B
8.龙一鸣和李菲菲从圆形操场的同一点出发,沿着操场的边相背而行,4分钟后两人相遇。龙一鸣每分钟走82米,李菲菲每分钟走75米,这个圆形操场的直径是多少米?
9.(1)在如图所示的长方形中画一个最大的半圆,将其余部分涂上阴影。
(2)图中阴影部分的周长是( )厘米。
10.为了校庆,学校准备编排一套大型集体舞,60名学生围成两个套在一起的大小不同的圆圈,并且每个圆圈上人与人之间的间隔都一样,大圈半径6米,小圈半径4米。那么你知道内、外圈各应站多少名学生吗?
11.一匹马拴在树上,绳长4米,求这匹马走一圈是多少米?最多能吃到多大面积的草?
12.一种零件的横截面是一个圆环,外圈半径是0.5米,内圈半径是0.4米。这种零件横截面的面积是多少平方米?
13.如下图,小圆的半径是3cm,比较大圆面积与两个小圆面积的和,你发现了什么?
14.已知大正方形边长为40厘米,求如图阴影部分的面积.
15.达瓦叔叔家修建了一块半圆形羊圈,共用去51.4米长的栅栏(损耗不计)。这个羊圈的占地面积是多少平方米?
16.学校阅览室的窗户上面是半圆,下面是正方形(如图)。窗户的面积是多少平方米?
17.如图,阴影部分的周长是多少?(单位:厘米)
18.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部分的面积.
19.张大爷准备靠墙用栅栏围成一个养鸡舍(如图),半径是5米。
(1)围成这个养鸡舍,至少要用多长的栅栏?
(2)如果要扩建这个养鸡舍,把它的直径增加2米,这个养鸡舍的面积增加了多少?
20.如下图,公园里有4块扇形区域准备铺设草坪(单位:米)。请你帮助计算一下,铺设草坪的面积是多少平方米?
21.有一个边长是4米的正方形草场,在它的一组对角分别拴了一头牛,拴牛的绳长是4米。两头牛共同吃到草的面积是多少平方米?
22.音乐厅座位区是一个半圆形(如下图所示),可以容纳观众1800人。那么阴影部分一共可以容纳多少观众?
23.按要求画一画,填一填。(图中小方格的边长是1cm)
(1)把三角形ABC向左平移6格,画出平移后的图形。
(2)把三角形ABC绕点B顺时针旋转90°,画出旋转后的图形。
(3)旋转过程中,线段BC所扫过的面积是( )cm2。
24.转化是解决数学问题的一个重要思想方法。运用转化的方法可以把未知的知识转化成已知的知识,把复杂的问题转化成简单的问题。如在探究除数是小数的除法时,运用商不变的性质把除数是小数的除法转化成除数是整数的除法。又如在探究圆的面积的时候,把圆的面积转化成了长方形的面积。
(1)回想一下,在我们的学习中,哪些地方也运用了转化思想?
_______________________转化成___________________________来研究。
你还能用转化的数学思想方法来解决以下数学问题吗?
(2)计算下图的面积。(单位:厘米)
(3)如图,三个圆的半径都是1厘米,求阴影部分的面积。
参考答案:
1.1.8米
【详解】720÷2=360(周)
720÷(360+40)=1.8(米)
2.1585.2米
【分析】观察图形可知,运动场的一圈相当于一个直径是30米的圆周长加上2条85米的长度,根据圆周长公式:C=πd,用3.14×30+85×2即可求出运动场的一圈是多少米,再乘6即可求出6圈是多少米。
【详解】3.14×30+85×2
=94.2+170
=264.2(米)
264.2×6=1585.2(米)
答:奇思每天跑1585.2米。
【点睛】本题考查了圆周长公式的灵活应用。
3.(1)11.51m
(2)6小时
【分析】(1)因为时针走一圈是12小时,当大本钟的时针经过8小时即是走了圆周长的,求走过的路程即是求以275米为半径的圆周长的即可;
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了几小时,用走过的路程除以周长,结果即是时针走过的时间与12小时的分率,据此解答。
【详解】(1)3.14×2.75×2×
=8.635×2×
=17.27×
≈11.51(m)
答:时针的尖端走过的路程是11.51米。
(2)8.635÷(3.14×2.75×2)×12
=8.635÷17.27×12
=0.5×12
=6(小时)
答:时针走过了6小时。
【点睛】此题考查的是圆周长在实际生活中的应用,关键是把实际问题转化成数学问题进行解答。
4.37.68平方米
【分析】先求出滚筒的周长,根据圆的周长公式:周长=π×直径,求滚筒的周长;进而求出10周滚出的长度,宽就是滚筒的长,再根据长方形的面积公式:面积=长×宽;即可求出被压路面的面积。
【详解】3.14×0.8×10×1.5
=2.512×10×1.5
=25.12×1.5
=37.68(平方米)
答:这台压路机滚动10周压过的路面是37.68平方米。
【点睛】解答本题的关键是明白:被压路面是一个长方形,弄清楚其长和宽,即可求其面积。
5.(1)157根
(2)1570米
【分析】(1)先利用圆的周长公式求出牛栏的周长,再除以2,就是需要的木桩的根数;
(2)先利用圆的周长公式求出牛栏的周长,再乘5.
【详解】(1)2×3.14×50÷2,
=314÷2,
=157(根);
答:一圈一共要安装157根木桩.
(2)2×3.14×50×5
=314×5
=1570(米)
答:至少需要铁丝1570米.
6.1.50小时
【分析】根据题意可知,神舟十三号飞船距离地面400千米,它所在圆的半径为地球的半径+400千米,根据圆的周长公式:π×2×半径,求出飞船所在圆的周长,再根据时间=距离÷速度,求出飞船绕地球一周大约需要时间;保留两位小数,看千分位,再根据“四舍五入”法,进行解答。
【详解】1小时=3600秒
3.14×2×(6400+400)÷7.9÷3600
=6.28×6800÷7.9÷3600
=42704÷7.9÷3600
≈5405.56962÷3600
≈1.50(小时)
答:飞船绕地球飞行一周大约需要1.50小时。
【点睛】本题考查圆的周长公式的应用,关键明确飞船所在圆的周长;以及根据距离、时间、速度三者关系解答问题。
7.24平方厘米
【分析】如图,°,说明OCDA是个正方形,三角形BCD是个等腰直角三角形,圆的半径=梯形上底=梯形的高,半径×2=梯形下底,根据圆的半径=周长÷π÷2,梯形面积=(上底+下底)×高÷2,列式解答即可。
【详解】25.12÷3.14÷2=4(厘米)
4×2=8(厘米)
(4+8)×4÷2
=12×4÷2
=24(平方厘米)
答:梯形OABC的面积是24平方厘米。
【点睛】关键是理解梯形和圆之间的关系,掌握并灵活运用圆的周长和梯形面积公式。
8.200米
【分析】龙一鸣每分钟走82米,李菲菲每分钟走75米,把两个人的速度加起来,求出两人的速度和,再根据“速度和×相遇时间=路程”,代入数据即可求出这个操场的周长,利用圆的周长公式:,代入数据即可求出这个圆形操场的直径。
【详解】(82+75)×4÷3.14
=157×4÷3.14
=628÷3.14
=200(米)
答:这个圆形操场的直径是200米。
【点睛】此题的解题关键是利用速度和、相遇时间、路程三者之间的关系,根据圆的周长公式,从而解决实际的问题。
9.(1)见详解
(2)21.42
【分析】(1)观察图形可知,画出的最大半圆,圆心在长方形长的中点处,半径是3厘米,直径是6厘米。据此作图;
(2)圆的周长=3.14×直径,据此先求出直径是6厘米圆的周长,再除以2求出半圆的弧长。将半圆弧长加上长方形的一个长、两个宽,即可求出阴影部分的周长。
【详解】(1)如图:
(2)3.14×6÷2+6+3×2
=9.42+6+6
=21.42(厘米)
所以,图中阴影部分的周长是21.42厘米。
【点睛】本题考查了画半圆、阴影部分的周长,掌握圆的画法、圆的周长公式是解题的关键。
10.内圈24名,外圈36名
【分析】根据圆的周长公式C=2πr可知,大小两个圆的周长比等于它们的半径之比,又已知每个圆圈上人与人之间的间隔都一样,那么大小两个圆圈上站的人数之比就等于两个圆的周长之比;根据按比分配的方法,用总人数除以总份数求出一份数,再用一份数分别乘大小圆圈上的人数之比,即可求出内、外圈各应站的人数。
【详解】6∶4=3∶2
60÷(3+2)
=60÷5
=12(名)
内圈站:12×2=24(名)
外圈站:12×3=36(名)
答:内圈应站24名学生,外圈应站36名学生。
【点睛】掌握按比分配的解题方法,明确要分配的总量是多少,以及按照什么比进行分配,求出一份数是解题的关键。
11.25.12米;50.24平方米
【分析】由图可知,马的绳长就是这个圆的半径,求马走一圈的长度就是求这个圆的周长,求吃多大面积的草,就是求这个圆的面积,据此根据圆的周长公式:C=2πr,面积公式:S=πr2,把数据代入公式解答即可。
【详解】这匹马走一圈是:4×2×3.14
=8×3.14
=25.12(米)
能吃到草的面积:42×3.14
=16×3.14
=50.24(平方米)
答:这匹马走一圈是25.12米,最多能吃到50.24平方米的草。
【点睛】此题主要考查圆的周长及面积公式,熟记公式是关键。
12.0.2826平方米
【分析】根据圆环的面积公式:S=π(R2-r2),据此代入数值进行计算即可。
【详解】3.14×(0.52-0.42)
=3.14×(0.25-0.16)
=3.14×0.09
=0.2826(平方米)
答:这种零件横截面的面积是0.2826平方米。
【点睛】本题考查圆环的面积,熟记公式是解题的关键。
13.大圆面积是两个小圆面积的和的2倍
【分析】由图可知,大圆的半径是小圆半径的2倍,根据“s=πr ”求出大圆和小圆的面积即可,再找出它们之间的规律。
【详解】32×3.14×2
=28.26×2
=56.52(cm2);
(3×2)2×3.14
=36×3.14
=113.04(cm2);
113.04÷56.52=2;
所以大圆面积是两个小圆面积的和的2倍;
当小圆的半径是r时;
两个小圆面积的和:r2×π×2=2πr2;
大圆面积:(r×2)2×π=4πr2;
4πr2÷2πr2=2;
所以大圆面积是两个小圆面积的和的2倍。
【点睛】熟练掌握圆的面积公式是解答本题的关键。
14.456平方厘米
【详解】40÷2=20(厘米)
3.14×202
=3.14×400
=1256(平方厘米)
40×20÷2×2
=800÷2×2
=800(平方厘米)
1256﹣800=456(平方厘米)
答:阴影部分的面积是456平方厘米.
15.157m
【分析】半圆形周长=圆周长的一半+直径,已知铁栅栏长51.4米,根据圆的周长公式C=πd求出直径长,再根据圆的面积公式S=πr 求出半圆面积。
【详解】设圆直径为d,
πd+d=51.4
d=51.4÷(π+1)
d=20
羊圈的占地面积:3.14×(20÷2) ÷2
=3.14×100÷2
=157(平方米)
答:羊圈的占地面积是157平方米。
【点睛】此题考查了圆的周长和面积公式的灵活应用,解答此题关键是把实际问题转化成数学问题中,并找到对应的数量关系。
16.5.57平方米
【分析】窗户面积=半圆面积+正方形面积,半圆面积=πr ÷2,正方形面积=边长×边长,据此列式解答。
【详解】3.14×(2÷2) ÷2+2×2
=3.14×1÷2+4
=1.57+4
=5.57(平方米)
答:窗户的面积是5.57平方米。
【点睛】关键是掌握圆和正方形面积公式。
17.111.36厘米
【分析】阴影部分的周长=直径是36厘米的圆周长的一半+半径是36厘米、圆心角是30°的扇形的弧长+直径36厘米;据此解答即可.
【详解】3.14×36÷2+2×3.14×36×+36
=56.62+18.84+36
=111.36(厘米)
答:阴影部分的周长是111.36厘米.
18.3.5625平方厘米
【详解】解:将两个同样的图形拼在一起成为圆减等腰直角三角形
[π÷4-×5×5]÷2=(π-)÷2=3.5625平方厘米
19.(1)15.7米;(2)17.27平方米
【分析】(1)观察图形可知,栅栏的长度相当于一个半径是5米的圆周长的一半,根据圆的周长公式,用2×3.14×5÷2即可求出栅栏的长度;
(2)直径增加2米,则半径变为(5+2÷2)米,根据半圆面积S=πr2÷2,分别求出增加后的面积和增加前的面积,然后求出它们的差即可。
【详解】(1)2×3.14×5÷2
=3.14×5
=15.7(米)
答:至少需要15.7米长的栅栏。
(2)2÷2=1(米)
5+1=6(米)
3.14×62÷2
=3.14×36÷2
=56.52(平方米)
3.14×52÷2
=3.14×25÷2
=39.25(平方米)
56.52-39.25=17.27(平方米)
答:这个养鸡舍的面积增加了17.27平方米。
【点睛】本题考查了圆周长公式和圆面积公式的灵活应用。
20.9.42平方米
【分析】两个半径为2米、圆心角为45°的扇形可以合成一个半径为2米、圆心角为90°的扇形,两个半径为2米、圆心角为90°的扇形可以合成一个半径为2米、圆心角为180°的扇形,而一个半径为2米、圆心角为90°的扇形和一个半径为2米、圆心角为180°的扇形可以合成一个半径为2米,圆心角为(180+90)°的扇形,根据扇形的面积计算公式:,代入数据即可求出铺设草坪的面积是多少平方米。
【详解】根据分析得,
=
=
=
=(平方米)
答:铺设草坪的面积是9.42平方米。
【点睛】本题考查利用扇形面积解决实际问题。熟记并会灵活地将等半径的多个扇形的面积之和转化成一个大的扇形的面积是解本题的关键。
21.9.12平方米
【分析】如图两头牛共同吃到草的面积是图中叶子形状(阴影部分)的面积,连接叶子对角,阴影部分被分成完全相同的两部分,先用的圆形面积减去三角形的面积求出阴影面积的一半,最后再乘2即可求出两头牛共同吃到草的面积。
【详解】(3.14×424×4÷2)×2
=(3.14×1616÷2)×2
=(12.56-8)×2
=4.56×2
=9.12(平方米)
答:两头牛共同吃到草的面积是9.12平方米。
【点睛】通过作图的方式把所求面积分割成两部分,用的圆形面积减去三角形的面积的求出每部分的面积是解题的关键。
22.600人
【分析】半圆的圆心角是180°,阴影部分圆心角是60°;所以阴影部分面积是半圆面积的;可容纳观众的人数也是整个座位区容纳观众人数的。据此解答即可。
【详解】60÷180=
可以容纳观众:1800×=600(人)
答:阴影部分一共可以容纳观众600人。
【点睛】明确阴影部分面积是半圆面积的是解答此题的关键。
23.(1)(2)见详解
(3)12.56
【分析】(1)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(3)旋转过程中,线段BC所扫过形状是个半径4cm的扇形,根据扇形面积=πr2×,列式计算即可。
【详解】(1)(2)
(3)3.14×42×
=3.14×16×
=12.56(cm2)
【点睛】决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
24.(1)把三角形的面积;平行四边形的面积;(答案不唯一)
(2)25.12平方厘米;
(3)1.57平方厘米
【分析】(1)推导三角形的面积计算公式时,用两个完全一样的三角形拼成一个平行四边形,把三角形的面积转化为平行四边形的面积,根据“平行四边形的面积=底×高”推导出“三角形的面积=底×高÷2”;
(2)把不规则图形的面积转化为半圆的面积,利用“”求出图形的总面积;
(3)由三角形的内角和为180°可知,阴影部分三个扇形的圆心角合在一起是180°,把阴影部分的面积转化为半径为1厘米圆面积的一半,利用“”求出阴影部分的面积,据此解答。
【详解】(1)分析可知,把三角形的面积转化成平行四边形的面积来研究。(答案不唯一)
(2)3.14×42÷2
=50.24÷2
=25.12(平方厘米)
所以,这个图形的面积是25.12平方厘米。
(3)分析可知,阴影部分的面积是整个圆面积的一半。
3.14×12÷2
=3.14÷2
=1.57(平方厘米)
所以,阴影部分的面积是1.57平方厘米。
【点睛】本题主要考查转化思想在数学中的应用,掌握含圆的组合图形面积的计算方法以及三角形面积公式的推导过程是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第5单元圆应用题特训卷(拔高卷)数学六年级上册人教版
1.前轮在720米的距离里比后轮多转40周,如果后轮的周长是2米,求前轮的周长.
2.如图,一个椭圆形运动场,两端是由两个半圆组成的,奇思每天早晨都绕运动场跑6圈,奇思每天跑多少米?
3.大本钟——伦敦市的标志性建筑物,钟盘上时针的长度是2.75m。
(1)大本钟的时针经过8小时,时针的尖端走过的路程是多少米?(得数保留两位小数)
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了多少小时?
4.一台压路机的滚筒长1.5米,直径是0.8米,这台压路机滚动10周压过的路面是多少平方米?
5.牧民们打算在草原附近修建一共圆形的牛栏,半径为50米.
(1)如果每隔2米安装一根木桩,一圈一共要安装多少根木桩?
(2)如果用粗铁丝把这个牛栏围成5圈,(接头处忽略不计)至少需要铁丝多少米?
6.神舟十三号飞船在太空中绕地球飞行,飞行时离地面高度约400千米,每秒钟约飞行7.9千米,求飞船绕地球飞行一周大约需要多少小时。(地球半径约为6400千米,结果保留两位小数)
7.如图所示:圆的周长是25.12厘米,°,梯形OABC的面积是多少平方厘米?
A B
8.龙一鸣和李菲菲从圆形操场的同一点出发,沿着操场的边相背而行,4分钟后两人相遇。龙一鸣每分钟走82米,李菲菲每分钟走75米,这个圆形操场的直径是多少米?
9.(1)在如图所示的长方形中画一个最大的半圆,将其余部分涂上阴影。
(2)图中阴影部分的周长是( )厘米。
10.为了校庆,学校准备编排一套大型集体舞,60名学生围成两个套在一起的大小不同的圆圈,并且每个圆圈上人与人之间的间隔都一样,大圈半径6米,小圈半径4米。那么你知道内、外圈各应站多少名学生吗?
11.一匹马拴在树上,绳长4米,求这匹马走一圈是多少米?最多能吃到多大面积的草?
12.一种零件的横截面是一个圆环,外圈半径是0.5米,内圈半径是0.4米。这种零件横截面的面积是多少平方米?
13.如下图,小圆的半径是3cm,比较大圆面积与两个小圆面积的和,你发现了什么?
14.已知大正方形边长为40厘米,求如图阴影部分的面积.
15.达瓦叔叔家修建了一块半圆形羊圈,共用去51.4米长的栅栏(损耗不计)。这个羊圈的占地面积是多少平方米?
16.学校阅览室的窗户上面是半圆,下面是正方形(如图)。窗户的面积是多少平方米?
17.如图,阴影部分的周长是多少?(单位:厘米)
18.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部分的面积.
19.张大爷准备靠墙用栅栏围成一个养鸡舍(如图),半径是5米。
(1)围成这个养鸡舍,至少要用多长的栅栏?
(2)如果要扩建这个养鸡舍,把它的直径增加2米,这个养鸡舍的面积增加了多少?
20.如下图,公园里有4块扇形区域准备铺设草坪(单位:米)。请你帮助计算一下,铺设草坪的面积是多少平方米?
21.有一个边长是4米的正方形草场,在它的一组对角分别拴了一头牛,拴牛的绳长是4米。两头牛共同吃到草的面积是多少平方米?
22.音乐厅座位区是一个半圆形(如下图所示),可以容纳观众1800人。那么阴影部分一共可以容纳多少观众?
23.按要求画一画,填一填。(图中小方格的边长是1cm)
(1)把三角形ABC向左平移6格,画出平移后的图形。
(2)把三角形ABC绕点B顺时针旋转90°,画出旋转后的图形。
(3)旋转过程中,线段BC所扫过的面积是( )cm2。
24.转化是解决数学问题的一个重要思想方法。运用转化的方法可以把未知的知识转化成已知的知识,把复杂的问题转化成简单的问题。如在探究除数是小数的除法时,运用商不变的性质把除数是小数的除法转化成除数是整数的除法。又如在探究圆的面积的时候,把圆的面积转化成了长方形的面积。
(1)回想一下,在我们的学习中,哪些地方也运用了转化思想?
_______________________转化成___________________________来研究。
你还能用转化的数学思想方法来解决以下数学问题吗?
(2)计算下图的面积。(单位:厘米)
(3)如图,三个圆的半径都是1厘米,求阴影部分的面积。
参考答案:
1.1.8米
【详解】720÷2=360(周)
720÷(360+40)=1.8(米)
2.1585.2米
【分析】观察图形可知,运动场的一圈相当于一个直径是30米的圆周长加上2条85米的长度,根据圆周长公式:C=πd,用3.14×30+85×2即可求出运动场的一圈是多少米,再乘6即可求出6圈是多少米。
【详解】3.14×30+85×2
=94.2+170
=264.2(米)
264.2×6=1585.2(米)
答:奇思每天跑1585.2米。
【点睛】本题考查了圆周长公式的灵活应用。
3.(1)11.51m
(2)6小时
【分析】(1)因为时针走一圈是12小时,当大本钟的时针经过8小时即是走了圆周长的,求走过的路程即是求以275米为半径的圆周长的即可;
(2)如果这个时钟的时针尖端走过的路程是8.635m,则时针走过了几小时,用走过的路程除以周长,结果即是时针走过的时间与12小时的分率,据此解答。
【详解】(1)3.14×2.75×2×
=8.635×2×
=17.27×
≈11.51(m)
答:时针的尖端走过的路程是11.51米。
(2)8.635÷(3.14×2.75×2)×12
=8.635÷17.27×12
=0.5×12
=6(小时)
答:时针走过了6小时。
【点睛】此题考查的是圆周长在实际生活中的应用,关键是把实际问题转化成数学问题进行解答。
4.37.68平方米
【分析】先求出滚筒的周长,根据圆的周长公式:周长=π×直径,求滚筒的周长;进而求出10周滚出的长度,宽就是滚筒的长,再根据长方形的面积公式:面积=长×宽;即可求出被压路面的面积。
【详解】3.14×0.8×10×1.5
=2.512×10×1.5
=25.12×1.5
=37.68(平方米)
答:这台压路机滚动10周压过的路面是37.68平方米。
【点睛】解答本题的关键是明白:被压路面是一个长方形,弄清楚其长和宽,即可求其面积。
5.(1)157根
(2)1570米
【分析】(1)先利用圆的周长公式求出牛栏的周长,再除以2,就是需要的木桩的根数;
(2)先利用圆的周长公式求出牛栏的周长,再乘5.
【详解】(1)2×3.14×50÷2,
=314÷2,
=157(根);
答:一圈一共要安装157根木桩.
(2)2×3.14×50×5
=314×5
=1570(米)
答:至少需要铁丝1570米.
6.1.50小时
【分析】根据题意可知,神舟十三号飞船距离地面400千米,它所在圆的半径为地球的半径+400千米,根据圆的周长公式:π×2×半径,求出飞船所在圆的周长,再根据时间=距离÷速度,求出飞船绕地球一周大约需要时间;保留两位小数,看千分位,再根据“四舍五入”法,进行解答。
【详解】1小时=3600秒
3.14×2×(6400+400)÷7.9÷3600
=6.28×6800÷7.9÷3600
=42704÷7.9÷3600
≈5405.56962÷3600
≈1.50(小时)
答:飞船绕地球飞行一周大约需要1.50小时。
【点睛】本题考查圆的周长公式的应用,关键明确飞船所在圆的周长;以及根据距离、时间、速度三者关系解答问题。
7.24平方厘米
【分析】如图,°,说明OCDA是个正方形,三角形BCD是个等腰直角三角形,圆的半径=梯形上底=梯形的高,半径×2=梯形下底,根据圆的半径=周长÷π÷2,梯形面积=(上底+下底)×高÷2,列式解答即可。
【详解】25.12÷3.14÷2=4(厘米)
4×2=8(厘米)
(4+8)×4÷2
=12×4÷2
=24(平方厘米)
答:梯形OABC的面积是24平方厘米。
【点睛】关键是理解梯形和圆之间的关系,掌握并灵活运用圆的周长和梯形面积公式。
8.200米
【分析】龙一鸣每分钟走82米,李菲菲每分钟走75米,把两个人的速度加起来,求出两人的速度和,再根据“速度和×相遇时间=路程”,代入数据即可求出这个操场的周长,利用圆的周长公式:,代入数据即可求出这个圆形操场的直径。
【详解】(82+75)×4÷3.14
=157×4÷3.14
=628÷3.14
=200(米)
答:这个圆形操场的直径是200米。
【点睛】此题的解题关键是利用速度和、相遇时间、路程三者之间的关系,根据圆的周长公式,从而解决实际的问题。
9.(1)见详解
(2)21.42
【分析】(1)观察图形可知,画出的最大半圆,圆心在长方形长的中点处,半径是3厘米,直径是6厘米。据此作图;
(2)圆的周长=3.14×直径,据此先求出直径是6厘米圆的周长,再除以2求出半圆的弧长。将半圆弧长加上长方形的一个长、两个宽,即可求出阴影部分的周长。
【详解】(1)如图:
(2)3.14×6÷2+6+3×2
=9.42+6+6
=21.42(厘米)
所以,图中阴影部分的周长是21.42厘米。
【点睛】本题考查了画半圆、阴影部分的周长,掌握圆的画法、圆的周长公式是解题的关键。
10.内圈24名,外圈36名
【分析】根据圆的周长公式C=2πr可知,大小两个圆的周长比等于它们的半径之比,又已知每个圆圈上人与人之间的间隔都一样,那么大小两个圆圈上站的人数之比就等于两个圆的周长之比;根据按比分配的方法,用总人数除以总份数求出一份数,再用一份数分别乘大小圆圈上的人数之比,即可求出内、外圈各应站的人数。
【详解】6∶4=3∶2
60÷(3+2)
=60÷5
=12(名)
内圈站:12×2=24(名)
外圈站:12×3=36(名)
答:内圈应站24名学生,外圈应站36名学生。
【点睛】掌握按比分配的解题方法,明确要分配的总量是多少,以及按照什么比进行分配,求出一份数是解题的关键。
11.25.12米;50.24平方米
【分析】由图可知,马的绳长就是这个圆的半径,求马走一圈的长度就是求这个圆的周长,求吃多大面积的草,就是求这个圆的面积,据此根据圆的周长公式:C=2πr,面积公式:S=πr2,把数据代入公式解答即可。
【详解】这匹马走一圈是:4×2×3.14
=8×3.14
=25.12(米)
能吃到草的面积:42×3.14
=16×3.14
=50.24(平方米)
答:这匹马走一圈是25.12米,最多能吃到50.24平方米的草。
【点睛】此题主要考查圆的周长及面积公式,熟记公式是关键。
12.0.2826平方米
【分析】根据圆环的面积公式:S=π(R2-r2),据此代入数值进行计算即可。
【详解】3.14×(0.52-0.42)
=3.14×(0.25-0.16)
=3.14×0.09
=0.2826(平方米)
答:这种零件横截面的面积是0.2826平方米。
【点睛】本题考查圆环的面积,熟记公式是解题的关键。
13.大圆面积是两个小圆面积的和的2倍
【分析】由图可知,大圆的半径是小圆半径的2倍,根据“s=πr ”求出大圆和小圆的面积即可,再找出它们之间的规律。
【详解】32×3.14×2
=28.26×2
=56.52(cm2);
(3×2)2×3.14
=36×3.14
=113.04(cm2);
113.04÷56.52=2;
所以大圆面积是两个小圆面积的和的2倍;
当小圆的半径是r时;
两个小圆面积的和:r2×π×2=2πr2;
大圆面积:(r×2)2×π=4πr2;
4πr2÷2πr2=2;
所以大圆面积是两个小圆面积的和的2倍。
【点睛】熟练掌握圆的面积公式是解答本题的关键。
14.456平方厘米
【详解】40÷2=20(厘米)
3.14×202
=3.14×400
=1256(平方厘米)
40×20÷2×2
=800÷2×2
=800(平方厘米)
1256﹣800=456(平方厘米)
答:阴影部分的面积是456平方厘米.
15.157m
【分析】半圆形周长=圆周长的一半+直径,已知铁栅栏长51.4米,根据圆的周长公式C=πd求出直径长,再根据圆的面积公式S=πr 求出半圆面积。
【详解】设圆直径为d,
πd+d=51.4
d=51.4÷(π+1)
d=20
羊圈的占地面积:3.14×(20÷2) ÷2
=3.14×100÷2
=157(平方米)
答:羊圈的占地面积是157平方米。
【点睛】此题考查了圆的周长和面积公式的灵活应用,解答此题关键是把实际问题转化成数学问题中,并找到对应的数量关系。
16.5.57平方米
【分析】窗户面积=半圆面积+正方形面积,半圆面积=πr ÷2,正方形面积=边长×边长,据此列式解答。
【详解】3.14×(2÷2) ÷2+2×2
=3.14×1÷2+4
=1.57+4
=5.57(平方米)
答:窗户的面积是5.57平方米。
【点睛】关键是掌握圆和正方形面积公式。
17.111.36厘米
【分析】阴影部分的周长=直径是36厘米的圆周长的一半+半径是36厘米、圆心角是30°的扇形的弧长+直径36厘米;据此解答即可.
【详解】3.14×36÷2+2×3.14×36×+36
=56.62+18.84+36
=111.36(厘米)
答:阴影部分的周长是111.36厘米.
18.3.5625平方厘米
【详解】解:将两个同样的图形拼在一起成为圆减等腰直角三角形
[π÷4-×5×5]÷2=(π-)÷2=3.5625平方厘米
19.(1)15.7米;(2)17.27平方米
【分析】(1)观察图形可知,栅栏的长度相当于一个半径是5米的圆周长的一半,根据圆的周长公式,用2×3.14×5÷2即可求出栅栏的长度;
(2)直径增加2米,则半径变为(5+2÷2)米,根据半圆面积S=πr2÷2,分别求出增加后的面积和增加前的面积,然后求出它们的差即可。
【详解】(1)2×3.14×5÷2
=3.14×5
=15.7(米)
答:至少需要15.7米长的栅栏。
(2)2÷2=1(米)
5+1=6(米)
3.14×62÷2
=3.14×36÷2
=56.52(平方米)
3.14×52÷2
=3.14×25÷2
=39.25(平方米)
56.52-39.25=17.27(平方米)
答:这个养鸡舍的面积增加了17.27平方米。
【点睛】本题考查了圆周长公式和圆面积公式的灵活应用。
20.9.42平方米
【分析】两个半径为2米、圆心角为45°的扇形可以合成一个半径为2米、圆心角为90°的扇形,两个半径为2米、圆心角为90°的扇形可以合成一个半径为2米、圆心角为180°的扇形,而一个半径为2米、圆心角为90°的扇形和一个半径为2米、圆心角为180°的扇形可以合成一个半径为2米,圆心角为(180+90)°的扇形,根据扇形的面积计算公式:,代入数据即可求出铺设草坪的面积是多少平方米。
【详解】根据分析得,
=
=
=
=(平方米)
答:铺设草坪的面积是9.42平方米。
【点睛】本题考查利用扇形面积解决实际问题。熟记并会灵活地将等半径的多个扇形的面积之和转化成一个大的扇形的面积是解本题的关键。
21.9.12平方米
【分析】如图两头牛共同吃到草的面积是图中叶子形状(阴影部分)的面积,连接叶子对角,阴影部分被分成完全相同的两部分,先用的圆形面积减去三角形的面积求出阴影面积的一半,最后再乘2即可求出两头牛共同吃到草的面积。
【详解】(3.14×424×4÷2)×2
=(3.14×1616÷2)×2
=(12.56-8)×2
=4.56×2
=9.12(平方米)
答:两头牛共同吃到草的面积是9.12平方米。
【点睛】通过作图的方式把所求面积分割成两部分,用的圆形面积减去三角形的面积的求出每部分的面积是解题的关键。
22.600人
【分析】半圆的圆心角是180°,阴影部分圆心角是60°;所以阴影部分面积是半圆面积的;可容纳观众的人数也是整个座位区容纳观众人数的。据此解答即可。
【详解】60÷180=
可以容纳观众:1800×=600(人)
答:阴影部分一共可以容纳观众600人。
【点睛】明确阴影部分面积是半圆面积的是解答此题的关键。
23.(1)(2)见详解
(3)12.56
【分析】(1)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(3)旋转过程中,线段BC所扫过形状是个半径4cm的扇形,根据扇形面积=πr2×,列式计算即可。
【详解】(1)(2)
(3)3.14×42×
=3.14×16×
=12.56(cm2)
【点睛】决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。决定旋转后图形的位置的要素:一是旋转中心或轴,二是旋转方向(顺时针或逆时针),三是旋转角度。
24.(1)把三角形的面积;平行四边形的面积;(答案不唯一)
(2)25.12平方厘米;
(3)1.57平方厘米
【分析】(1)推导三角形的面积计算公式时,用两个完全一样的三角形拼成一个平行四边形,把三角形的面积转化为平行四边形的面积,根据“平行四边形的面积=底×高”推导出“三角形的面积=底×高÷2”;
(2)把不规则图形的面积转化为半圆的面积,利用“”求出图形的总面积;
(3)由三角形的内角和为180°可知,阴影部分三个扇形的圆心角合在一起是180°,把阴影部分的面积转化为半径为1厘米圆面积的一半,利用“”求出阴影部分的面积,据此解答。
【详解】(1)分析可知,把三角形的面积转化成平行四边形的面积来研究。(答案不唯一)
(2)3.14×42÷2
=50.24÷2
=25.12(平方厘米)
所以,这个图形的面积是25.12平方厘米。
(3)分析可知,阴影部分的面积是整个圆面积的一半。
3.14×12÷2
=3.14÷2
=1.57(平方厘米)
所以,阴影部分的面积是1.57平方厘米。
【点睛】本题主要考查转化思想在数学中的应用,掌握含圆的组合图形面积的计算方法以及三角形面积公式的推导过程是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
