《用字母解决问题》课件(共20张PPT)人教版五年级上册数学
文档属性
| 名称 | 《用字母解决问题》课件(共20张PPT)人教版五年级上册数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-14 18:12:16 | ||
图片预览



文档简介
(共20张PPT)
用字母解决问题
创设情境
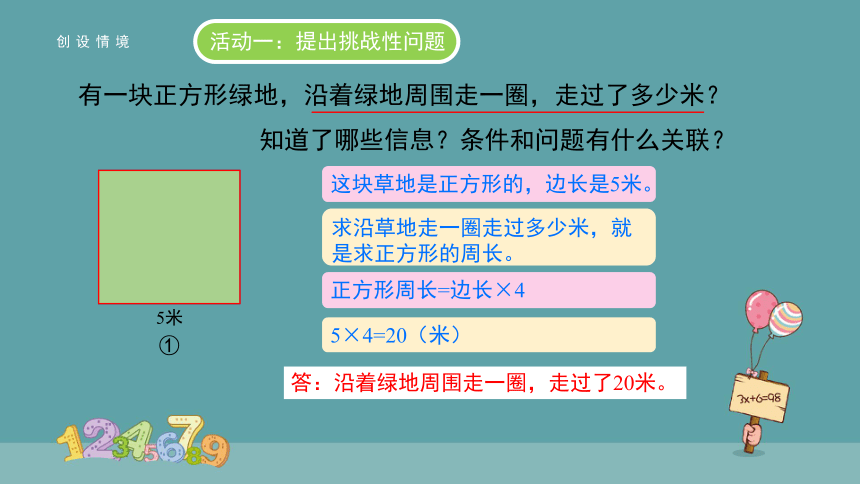
活动一:提出挑战性问题
①
5米
有一块正方形绿地,沿着绿地周围走一圈,走过了多少米?
知道了哪些信息?条件和问题有什么关联?
这块草地是正方形的,边长是5米。
求沿草地走一圈走过多少米,就是求正方形的周长。
正方形周长=边长×4
5×4=20(米)
答:沿着绿地周围走一圈,走过了20米。
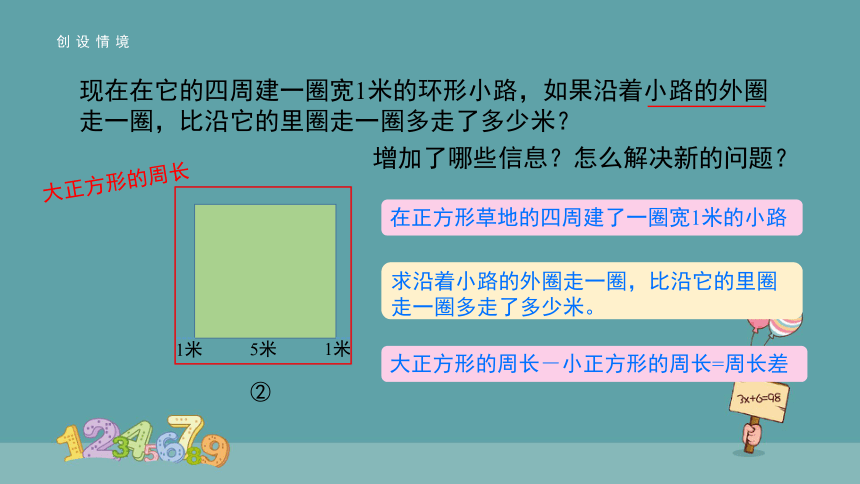
创设情境
5米
1米
1米
②
现在在它的四周建一圈宽1米的环形小路,如果沿着小路的外圈走一圈,比沿它的里圈走一圈多走了多少米?
增加了哪些信息?怎么解决新的问题?
在正方形草地的四周建了一圈宽1米的小路
求沿着小路的外圈走一圈,比沿它的里圈走一圈多走了多少米。
大正方形的周长-小正方形的周长=周长差
大正方形的周长
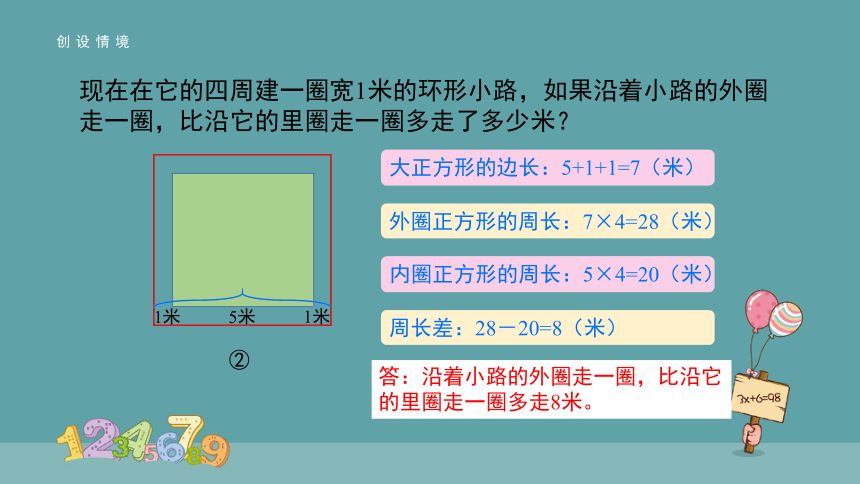
创设情境
5米
1米
1米
②
大正方形的边长:5+1+1=7(米)
外圈正方形的周长:7×4=28(米)
内圈正方形的周长:5×4=20(米)
周长差:28-20=8(米)
答:沿着小路的外圈走一圈,比沿它的里圈走一圈多走8米。
现在在它的四周建一圈宽1米的环形小路,如果沿着小路的外圈走一圈,比沿它的里圈走一圈多走了多少米?
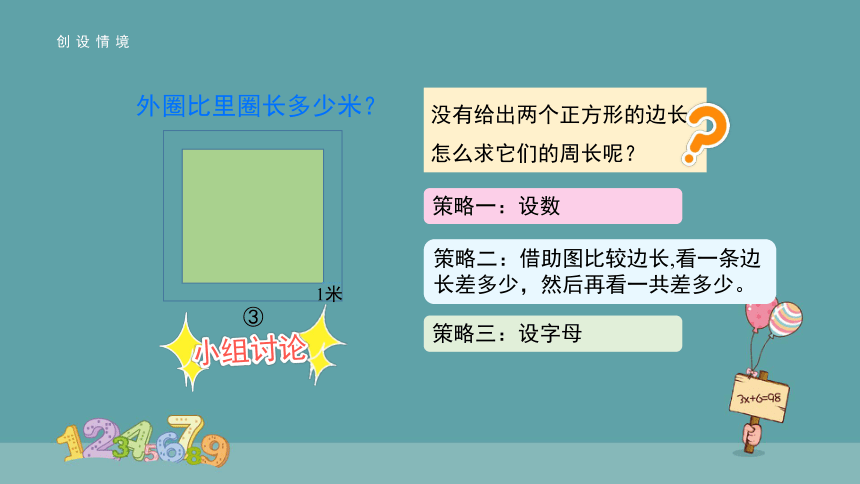
创设情境
1米
还有一块正方形绿地,在它的四周修一条宽1米的环形小路。现在,沿着小路的外圈走一圈比沿它的里圈走一圈多了多少米
外圈比里圈长多少米?
③
没有给出两个正方形的边长,怎么求它们的周长呢?
问题相同
问题相同
创设情境
策略一:设数
策略二:借助图比较边长,看一条边长差多少,然后再看一共差多少。
策略三:设字母
没有给出两个正方形的边长,怎么求它们的周长呢?
1米
外圈比里圈长多少米?
③
小组讨论
小组讨论
探究新知
设里圈边长为2米
外边长:2+1+1=4(米)
外圈长:4×4=16(米)
里圈长:2×4=8(米)
周长差: 16-8=8(米)
答:外圈比里圈长8米。
活动二:尝试“用字母” 解决问题
1米
外圈比里圈长多少米?
③
方法一:设数解决问题
方法一:设数解决问题
探究新知
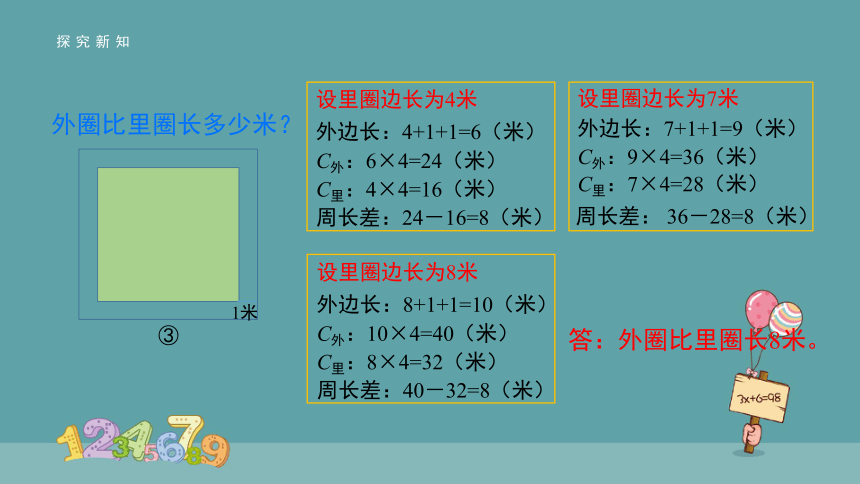
设里圈边长为4米
外边长:4+1+1=6(米)
C外:6×4=24(米)
C里:4×4=16(米)
周长差:24-16=8(米)
设里圈边长为8米
外边长:8+1+1=10(米)
C外:10×4=40(米)
C里:8×4=32(米)
周长差:40-32=8(米)
设里圈边长为7米
外边长:7+1+1=9(米)
C外:9×4=36(米)
C里:7×4=28(米)
周长差: 36-28=8(米)
答:外圈比里圈长8米。
1米
外圈比里圈长多少米?
③
探究新知
1米
外圈比里圈长多少米?
③
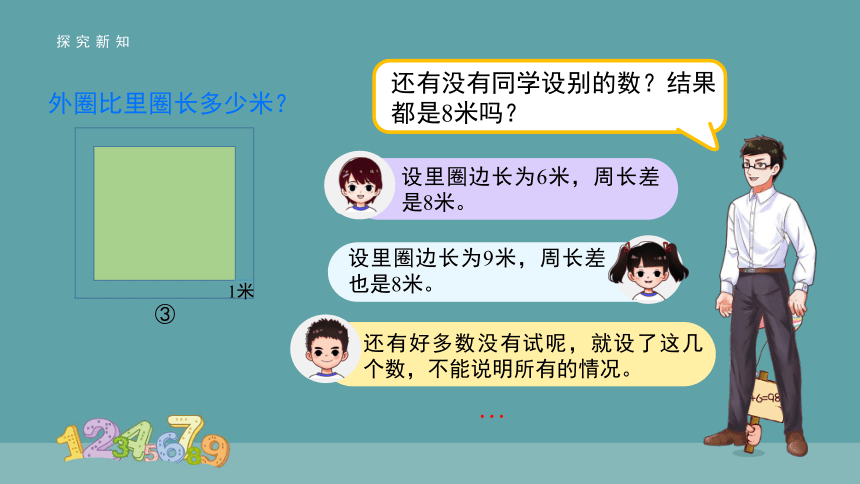
还有没有同学设别的数?结果都是8米吗?
设里圈边长为6米,周长差是8米。
设里圈边长为9米,周长差也是8米。
…
还有好多数没有试呢,就设了这几个数,不能说明所有的情况。
探究新知
将内边长设为x米
内周长:x×4=4x(米)
外周长:x+2×4=x+8(米)
周长差:x+8-4x= 米
将里圈边长设为x米
外圈边长:x+1×2=x+2(米)
外圈周长:4(x+2)=4x+2×4=4x+8(米)
里圈周长:4×x=4x(米)
外-里: 4x+8-4x=8(米)
1米
外圈比里圈长多少米?
③
能不能只设一个算式,就能表示所有情况呢?
探究新知
相同点:都把内圈边长设为x,内圈周长表示为4x
1米
外圈比里圈长多少米?
③
比较两种方法
将内边长设为x ,
内周长:x×4=4×x
外周长:x+2×4=x+8(米)
周长差:x+8-4x= (米)
将里圈边长设为x,
外圈边长:x+1×2=x+2
外圈周长:4×(x+2)=4x+2×4
=4x+8
里圈周长:4×x=4x(米)
外-里: 4x+8-4x=8(米)
探究新知
将内边长设为x ,
内周长:x×4=4×x
外周长:x+2×4=x+8(米)
周长差:x+8-4x= (米)
将里圈边长设为x,
外圈边长为:x+1×2=x+2
外圈周长为:4×(x+2)=4x+2×4
=4x+8
里圈周长4×x=4x(米)
外-里: 4x+8-4x=8(米)
不同点:外圈周长不同
不是外圈周长
用乘法分配律化简
外周长:4x+2×4=4x+8
周长差:4x+8-4x=8(米)
加4x同减4x直接抵消
1米
外圈比里圈长多少米?
③
比较两种方法
答:外圈比里圈长8米。
应用巩固
多出8段,每段是1米,8段就是8米。
把里圈边长和外圈边长重叠的部分抵消掉。
1米
1米
1米
1米
1米
1米
1米
1米
所以4x+8-4x=8
活动三:交流“用图形”解决问题
小组讨论:说一说为什么4x+8-4x=8。
外圈比里圈长多少米?
外圈每一条边都比里圈多2米
4条边一共多出 2×4=8(米)
2米
应用巩固
小组讨论:说一说为什么4x+8-4x=8。
外圈比里圈长多少米?
所以4x+8-4x=8
1米
1米
两个4x相互抵消
设里圈边长为x
1米
x
x
x
x
x
x
x
x
1米
1米
1米
1米
1米
1米
1米
应用巩固
小组讨论:说一说为什么4x+8-4x=8。
所以4x+8-4x=8
外圈比里圈长多少米?
1米
外圈比里圈长多少米?
③
设数
应用巩固
设字母
画图
不全面,设不完所有的数
字母可以代表任何数
直观感受外圈和内圈边的关系
用字母不仅能表示设的所有的数,而且它也能参与运算,这是一个很重要的解决问题的方法。
活动四:回顾与反思
没有给出两个正方形的边长,怎么求它们的周长呢?
课堂小结
今天的学习你有什么收获?
寻找解决策略
问题激发认知需要
设数
设字母
图形
验证
用字母解决问题
多方法解决问题
研究途径
探究方法
体会字母表示的一般性
拓展延伸
牧场上长满牧草,每天牧草都匀速生长。这片牧场可供10头羊吃20天,可供15头羊吃10天,供25头羊可吃几天
供剩下20头羊需要:100x÷ (20×x)=5(天)
设1头羊1天的吃草量为x,
10头羊吃20天共吃了: x×10×20=200x份,
15头羊吃10天共吃了: x×15×10=150x份,
第一种吃法比第二种吃法多吃了:200 x-150x =50x份草,
这50x份草是牧场20-10=10(天)生长出来的,
所以每天生长的草量为:50x ÷10=5x份,
那么原有草量为: 200x -5x ×20=100x,
25头羊吃,若有5头羊去吃每天生长的草,
答:它可供25头羊吃5天。
可以设字母解决问题
可以设字母解决问题
课后活动
你能利用下面的图发现(a+b)2=a2+2ab+b2
这一公式吗?利用你所学的面积计算的知
识,探索一下。
a
b
a
b
再见!
用字母解决问题
创设情境
活动一:提出挑战性问题
①
5米
有一块正方形绿地,沿着绿地周围走一圈,走过了多少米?
知道了哪些信息?条件和问题有什么关联?
这块草地是正方形的,边长是5米。
求沿草地走一圈走过多少米,就是求正方形的周长。
正方形周长=边长×4
5×4=20(米)
答:沿着绿地周围走一圈,走过了20米。
创设情境
5米
1米
1米
②
现在在它的四周建一圈宽1米的环形小路,如果沿着小路的外圈走一圈,比沿它的里圈走一圈多走了多少米?
增加了哪些信息?怎么解决新的问题?
在正方形草地的四周建了一圈宽1米的小路
求沿着小路的外圈走一圈,比沿它的里圈走一圈多走了多少米。
大正方形的周长-小正方形的周长=周长差
大正方形的周长
创设情境
5米
1米
1米
②
大正方形的边长:5+1+1=7(米)
外圈正方形的周长:7×4=28(米)
内圈正方形的周长:5×4=20(米)
周长差:28-20=8(米)
答:沿着小路的外圈走一圈,比沿它的里圈走一圈多走8米。
现在在它的四周建一圈宽1米的环形小路,如果沿着小路的外圈走一圈,比沿它的里圈走一圈多走了多少米?
创设情境
1米
还有一块正方形绿地,在它的四周修一条宽1米的环形小路。现在,沿着小路的外圈走一圈比沿它的里圈走一圈多了多少米
外圈比里圈长多少米?
③
没有给出两个正方形的边长,怎么求它们的周长呢?
问题相同
问题相同
创设情境
策略一:设数
策略二:借助图比较边长,看一条边长差多少,然后再看一共差多少。
策略三:设字母
没有给出两个正方形的边长,怎么求它们的周长呢?
1米
外圈比里圈长多少米?
③
小组讨论
小组讨论
探究新知
设里圈边长为2米
外边长:2+1+1=4(米)
外圈长:4×4=16(米)
里圈长:2×4=8(米)
周长差: 16-8=8(米)
答:外圈比里圈长8米。
活动二:尝试“用字母” 解决问题
1米
外圈比里圈长多少米?
③
方法一:设数解决问题
方法一:设数解决问题
探究新知
设里圈边长为4米
外边长:4+1+1=6(米)
C外:6×4=24(米)
C里:4×4=16(米)
周长差:24-16=8(米)
设里圈边长为8米
外边长:8+1+1=10(米)
C外:10×4=40(米)
C里:8×4=32(米)
周长差:40-32=8(米)
设里圈边长为7米
外边长:7+1+1=9(米)
C外:9×4=36(米)
C里:7×4=28(米)
周长差: 36-28=8(米)
答:外圈比里圈长8米。
1米
外圈比里圈长多少米?
③
探究新知
1米
外圈比里圈长多少米?
③
还有没有同学设别的数?结果都是8米吗?
设里圈边长为6米,周长差是8米。
设里圈边长为9米,周长差也是8米。
…
还有好多数没有试呢,就设了这几个数,不能说明所有的情况。
探究新知
将内边长设为x米
内周长:x×4=4x(米)
外周长:x+2×4=x+8(米)
周长差:x+8-4x= 米
将里圈边长设为x米
外圈边长:x+1×2=x+2(米)
外圈周长:4(x+2)=4x+2×4=4x+8(米)
里圈周长:4×x=4x(米)
外-里: 4x+8-4x=8(米)
1米
外圈比里圈长多少米?
③
能不能只设一个算式,就能表示所有情况呢?
探究新知
相同点:都把内圈边长设为x,内圈周长表示为4x
1米
外圈比里圈长多少米?
③
比较两种方法
将内边长设为x ,
内周长:x×4=4×x
外周长:x+2×4=x+8(米)
周长差:x+8-4x= (米)
将里圈边长设为x,
外圈边长:x+1×2=x+2
外圈周长:4×(x+2)=4x+2×4
=4x+8
里圈周长:4×x=4x(米)
外-里: 4x+8-4x=8(米)
探究新知
将内边长设为x ,
内周长:x×4=4×x
外周长:x+2×4=x+8(米)
周长差:x+8-4x= (米)
将里圈边长设为x,
外圈边长为:x+1×2=x+2
外圈周长为:4×(x+2)=4x+2×4
=4x+8
里圈周长4×x=4x(米)
外-里: 4x+8-4x=8(米)
不同点:外圈周长不同
不是外圈周长
用乘法分配律化简
外周长:4x+2×4=4x+8
周长差:4x+8-4x=8(米)
加4x同减4x直接抵消
1米
外圈比里圈长多少米?
③
比较两种方法
答:外圈比里圈长8米。
应用巩固
多出8段,每段是1米,8段就是8米。
把里圈边长和外圈边长重叠的部分抵消掉。
1米
1米
1米
1米
1米
1米
1米
1米
所以4x+8-4x=8
活动三:交流“用图形”解决问题
小组讨论:说一说为什么4x+8-4x=8。
外圈比里圈长多少米?
外圈每一条边都比里圈多2米
4条边一共多出 2×4=8(米)
2米
应用巩固
小组讨论:说一说为什么4x+8-4x=8。
外圈比里圈长多少米?
所以4x+8-4x=8
1米
1米
两个4x相互抵消
设里圈边长为x
1米
x
x
x
x
x
x
x
x
1米
1米
1米
1米
1米
1米
1米
应用巩固
小组讨论:说一说为什么4x+8-4x=8。
所以4x+8-4x=8
外圈比里圈长多少米?
1米
外圈比里圈长多少米?
③
设数
应用巩固
设字母
画图
不全面,设不完所有的数
字母可以代表任何数
直观感受外圈和内圈边的关系
用字母不仅能表示设的所有的数,而且它也能参与运算,这是一个很重要的解决问题的方法。
活动四:回顾与反思
没有给出两个正方形的边长,怎么求它们的周长呢?
课堂小结
今天的学习你有什么收获?
寻找解决策略
问题激发认知需要
设数
设字母
图形
验证
用字母解决问题
多方法解决问题
研究途径
探究方法
体会字母表示的一般性
拓展延伸
牧场上长满牧草,每天牧草都匀速生长。这片牧场可供10头羊吃20天,可供15头羊吃10天,供25头羊可吃几天
供剩下20头羊需要:100x÷ (20×x)=5(天)
设1头羊1天的吃草量为x,
10头羊吃20天共吃了: x×10×20=200x份,
15头羊吃10天共吃了: x×15×10=150x份,
第一种吃法比第二种吃法多吃了:200 x-150x =50x份草,
这50x份草是牧场20-10=10(天)生长出来的,
所以每天生长的草量为:50x ÷10=5x份,
那么原有草量为: 200x -5x ×20=100x,
25头羊吃,若有5头羊去吃每天生长的草,
答:它可供25头羊吃5天。
可以设字母解决问题
可以设字母解决问题
课后活动
你能利用下面的图发现(a+b)2=a2+2ab+b2
这一公式吗?利用你所学的面积计算的知
识,探索一下。
a
b
a
b
再见!
